快慢車組合運行條件下市域快線節能坡優化模型與算法研究

曹金銘，李得偉，董欣壘，于婕

快慢車組合運行條件下市域快線節能坡優化模型與算法研究

曹金銘，李得偉，董欣壘，于婕

(北京交通大學交通運輸學院，北京 100044)

基于既有研究大多局限于站站停列車運行條件下的地鐵節能坡優化，為解決快慢車組合運行條件下市域快線節能坡優化問題，在對列車受力分析的基礎上，提出快慢車組合運行下列車運行能耗表達函數，并構建以運行能耗最小和列車運行時間偏離最小為目標的節能坡優化模型，并基于改進的遺傳算法設計快速求解算法。通過廣州市域快線18號線驗證，研究結果表明：本文所提模型與算法能夠有效求解節能坡設計方案，相對于原始方案，優化方案在保持運行時間小幅變動的前提下，使列車牽引能耗降低了15.2%~25.2%。并發現快慢車的不同比例對節能坡設計方案和節能效果有影響，慢車比例越大，方案的節能效果越顯著。

市域快線；節能坡；遺傳算法；快慢車組合運營

隨著我國城市化、區域化進程的加快，連接城市中心與衛星城鎮的大運量高速度的市域快線應運而生。市域快線作為城市軌道交通的一種制式，其速度高于地鐵，站間距長，運營模式多為快慢車組合運行[1]。為了更好地節省列車能耗、實現城市軌道交通可持續發展，從線路縱斷面優化設計角度考慮運營目標與列車能耗的相互協調，是一種長期且有效的方法[2]。節能坡優化設計問題在地鐵線路設計中有較為廣泛的研究基礎，并在實際得到運用[3?4]，在高速鐵路里也有少量研究[5?8]。對于市域快線，由于運行速度較高、部分列車存在跨站運行等特點，地鐵節能坡設計理論無法直接應用。同樣，由于線路性質不同、站間距不同，高速鐵路節能坡的相關理論也不能用于市域快線。因此急需要一種適應于市域快線運輸組織特點的節能坡優化設計方法。為了解決這一問題，本文研究提出了以列車牽引能耗最小和列車運行時間偏離最小為目標的節能坡優化模型，并設計改進的遺傳算法，高效求解快慢車組合運行的市域快線線路節能坡優化方案。為市域快線的線路設計提供理論支持。

1 市域快線節能坡優化問題定義

1.1 市域快線節能坡優化的特殊性

與站站停模式的普速地鐵不同，快慢車組合運行條件下市域快線的節能坡優化具有其特殊性，主要表現在以下2個方面：

1) 市域快線站間距長、運行速度高。市域快線站間距一般都在3 km以上，有些甚至超過了20 km，超過地鐵2～3 km的站間距。國內外運營市域快線的最高運行速度在100～160 km/h，遠遠高于地鐵60～70 km/h的運行速度。長站間距導致無法采用簡單的加速?惰行?制動的節能運行方式。

2) 運營組織靈活，采用快慢車組合運行形式，快車在大站停車，在小站跨站不停車，慢車站站停車，并且當快車經過小站不停車時需要在安全限速內運行。不同類型的停站模式會導致同一個車站的節能坡對一種列車節能而對另一種列車不節能的情況。

1.2 節能與節時矛盾的處理

節能與節時是城市軌道交通節能坡設計追求的2個目標，既節能又節時的設計方案是最優化方案。事實上，節能與節時往往是矛盾的[6]，在市域快線條件下，這個矛盾更為突出。為了滿足目標要求，在模型構建與算法設計時，在提升節能效果的基礎上對節時進行約束，增加時間懲罰系數，從而完成快速與節能的矛盾處理。

因此，市域快線節能坡優化問題可以概括為：對以較高速度運行、較長區間里程、多種停站模式結合的線路進行節能坡設計，使線路列車在滿足運行時間的同時實現能耗節省。

2 模型建立

市域快線列車運行過程受力與地鐵列車基本相同。列車運行過程中主要受力有牽引力和運行阻力，其中運行阻力包括基本運行阻力、曲線附加阻力及坡道附加阻力等。本部分在相關列車動力學[9]研究的基礎上，構建能耗表達函數，并建立節能坡設計優化模型。

2.1 列車運行能耗表達函數構建

為了滿足不同站間距運行時間的要求，本文研究的列車區間運行操縱策略有2種，分別為牽引惰行交替模式與巡航模式。交替模式下，列車運行過程可以分為列車啟動、牽引加速出站、區間牽引運行、撤除牽引惰行、制動減速進站5種運行工況，如圖1(a)。巡航模式下，列車的運行過程可以分為列車啟動、牽引加速出站、區間巡航運行、制動減速進站4種運行工況，如圖1(b)。對應不同工況分別進行能耗分析，并根據各車站間各部分工況能耗分析求和得到列車在線路上運行的總能耗。

為了便于運行能耗的表達與計算，規定車站1和車站2之間由x個等間隔里程構成，并認為在?內，牽引力和制動力不發生變化。本文中?為50 m。

2.1.1 列車交替運行模式下的能耗計算

1) 列車啟動能耗

啟動牽引力做功表示為：

式中：0為列車啟動瞬時最大牽引力；?為單位運行長度；為列車重量為。

(a) 交替模式工況；(b) 巡航模式工況

圖1 列車運行工況示意圖

Fig. 1 Schematic diagram of train operating state

2) 列車牽引加速工況下的牽引能耗

已知列車瞬時啟動后速度為1，1的計算可以由式(2)表示：

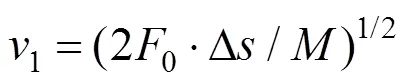
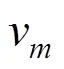
牽引能耗表示為：

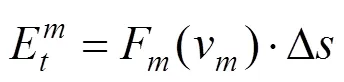
并可計算得出第個?內列車運行時間t

3) 列車區間運行能耗

故列車區間牽引能耗可表示為：

1和2為0-1變量，分別表示是否為牽引工況、是否為惰行工況。

4) 列車制動工況下的能耗

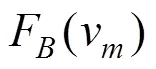
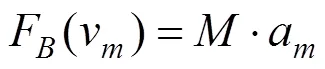
此里程間隔內的制動能耗表示為：

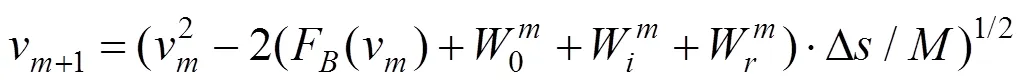
依次計算可以得出制動過程各個里程間隔的制動能耗。當列車達到最后一個里程間隔Δ時，列車的制動能耗為：

5) 列車交替模式下的區間總能耗

1為列車牽引加速出站過程中Δ的數量，3為列車制動減速進站過程中Δ的數量。

6) 列車全線總能耗

2.1.2 列車巡航模式下的能耗計算

列車巡航模式下，列車啟動到一定速度v后以該速度勻速運行，此時，動力等于阻力，因此牽引力的做功可以用阻力做功之和的形式來表示以建立與線路條件之間的關系：

因此，巡航模式下，列車區間運行能耗可表 示為：

2.1.3 快慢車全線運行總能耗表達函數

(a) 快車跨站；(b) 慢車停車

一般認為，在規范設計標準內，坡度越大對于進出站的列車節能效果越顯著，對于跨站的列車節能效果越不明顯，所以快車與慢車對于小站節能坡設計的要求是相悖的，為了探究不同快慢車比例下的節能坡方案與效果，將快慢車比例加入全線能耗計算。

交替模式下，快慢車全線運行總能耗可以表示為：

巡航模式下，快慢車全線運行總能耗可以表示為：

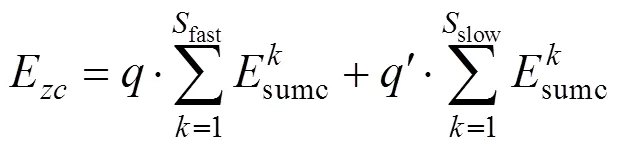
式中：和′分別表示快慢車比例系數。

2.2 節能坡優化模型

2.2.1 目標函數

同理，巡航模式下節能坡優化的目標函數可以表示為：

式中：t為時間偏離比例。

2.2.2 節能坡優化約束條件

1) 站坪長度約束

根據線路及列車基本數據及相關研究[11]，設置站坪長度為2S=200 m，車站的中心樁號為K。即區間上的第1個坡段(車站的出站坡)的起始位置與最后一個坡段(車站+1的進站坡)的終止位置，分別固定在K+100和K+1?100處。

2) 坡長約束

根據《市域快速軌道交通設計規范》[12]，坡段長度應大于坡段最小值min且相鄰豎曲線不重疊。同時為減小工程，滿足線路能力，坡段長度不應大于坡段最大值max；綜合以上條件確定坡長約束：

結合節能坡設計原則及《市域快速軌道交通設計規范》，對快慢車組合運行的車站進、出站節能坡坡長限制在一定的長度范圍，形成坡長約束 如下：

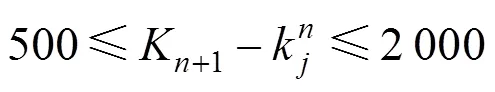
3) 坡度約束

根據設計規范及排水要求，縱斷面坡度最小值min應為1，根據地鐵設計規范規定，城市軌道交通線路正線的最大坡度max不宜大于30，困難地段可采用35。故坡度約束為：

4) 列車運行約束

3 改進遺傳算法

上述節能坡優化模型是非線性混合整數規劃問題，精確求解算法難以求得全局最優解。因此，本研究通過改進遺傳算法來實現求解。遺傳算法由于其高效的全局搜索能力與極大的靈活性的優點被廣泛應用。對算法中染色體編碼、初始解生成、適應度函數、變異與交叉算法等進行調整，使之適應模型的結構。

算法的具體步驟如下。

3.1 編碼設計

選擇便于大空間搜索且精度高的實數編碼方式對問題進行編碼操作。實數編碼分別對坡長和高程進行表示。其中染色體編碼第一行為坡長編碼，第二行為相鄰坡段高程差編碼，即前后2個變坡點高度差，在運算中，變坡點位置使用坡長累加值表示，坡度用高程差除以坡長表示。染色體具體編碼形式可見圖3。

圖3 染色體編碼圖

3.2 種群初始化

種群初始化過程中首先隨機產生初始縱斷面設計方案。初始解不規定變坡點的數量，使用坡長的長度約束來限定變坡點數量，以10 km的區間為例，坡長的約束為500 m至2 000 m，則變坡點數量的范圍區間為4至19個。

初始解生成思路為，隨機生成滿足約束的坡長與高程差，構建出一個基因片段，區間剩余長度與高程差減去該基因片段的坡長與高程差，直至區間剩余長度與高程差符合區間要求時停止。經過這種處理，產生了一組坡長、高程差，具有很強隨機性的初始解，可以有效提升算法求解質量。

3.3 適應度函數

適應度函數值是種群進化過程中唯一的選擇依據，是對每個可行解質量的一種度量，一般根據優化模型的目標函數計算可行解的適應度值。本算法中適應度函數為運行總能耗的倒數：

3.4 交叉

由于不同染色體的基因片段對應的變坡點里程不同，無法采用單點交叉或者多點交叉，考慮到這種情況，交叉算子采用三維空間算術交叉，將2條染色體進行空間上的交叉，若符合約束條件，則交叉成功。交叉后的子染色體′由進行交叉的雙親染色體1和2組合交叉而成，具體公式如下：

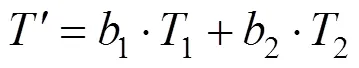
式中：1=0.5+；2=0.5?，為[0,1]的隨機數。

為了提升交叉成功率，若交叉的染色體不符合約束條件，則進行混合交叉，并改變直至符合約束條件。混合交叉公式如下：

3.5 變異

變異算子采用多點變異方法，即染色體上任意片段都可以變異，增強變異能力，提升求解全局最優解能力。為了提升搜索有效解的效率，變異調整使用正態分布處理，即變異幅度越大，可能性越小。若變異后的基因片段符合約束，則變異繼續，若不符合約束，則變異停止。變異公式如下：

3.6 終止

當問題收斂于最優解時，算法自動停止。為了確保結果的穩定，當進化達到最大進化代數時，進化終止。

4 案例驗證

選取廣州地鐵18號線作為案例，結合實際線路條件、運營資料等基本數據，對優化模型求解中需要采用的參數系數進行統一設置。

4.1 線路基本情況

廣州地鐵18號線是是國內首批可以實現地鐵服務水平的全地下市域快線之一，線路大致呈南北走向，全長60 km。列車參數見表1。列車實際運行模式為巡航模式，為驗證方法的有效性，本文求解中采用交替與巡航2種列車運行模式。

4.2 實驗結果

算法中參數取值如下：初始種群大小為20，交叉概率為0.65，變異概率為0.01，最大迭代次數為1 000。從圖4可以看出，最大適應度在320代降低到90后，趨于穩定，因此認為最大迭代數1 000可以滿足優化目標的要求，且算法收斂性較好。

表1 列車參數

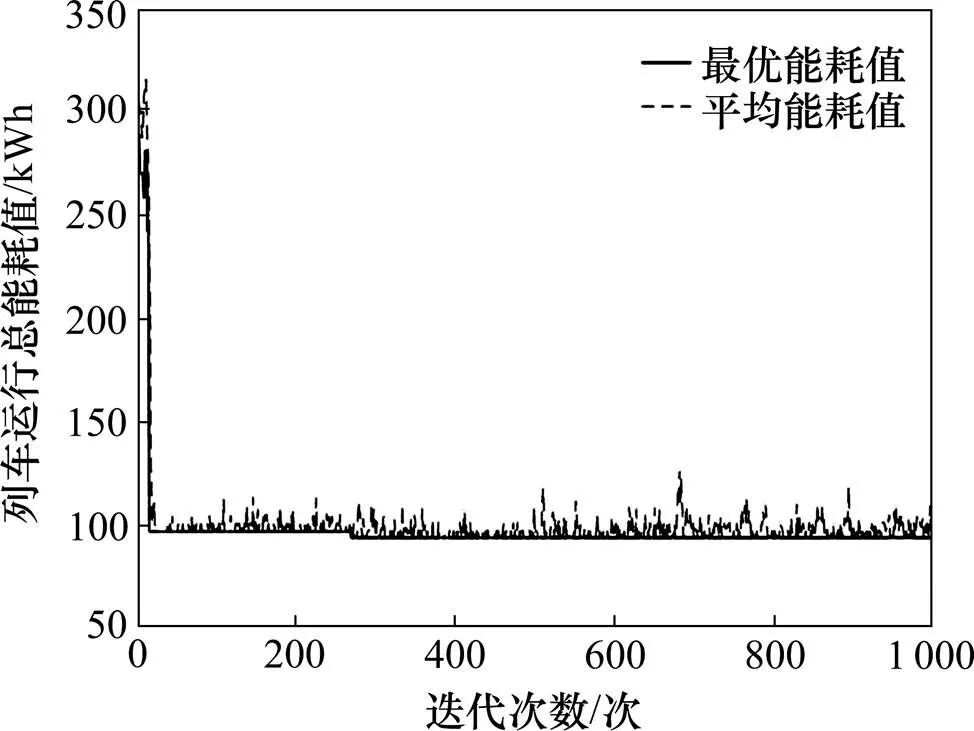
圖4 適應度變化曲線

單位：m

各個區間人工設計方案見圖5，第1行數字表示坡度，第2行數字表示坡長。考慮線路實際運營快慢車比例快車為37對，慢車為81對，接近1:2，故本節選取快慢車比例為1:2的線路設計方案作為展示，節能坡線路方案見圖6。

表2為快慢車比例為1:2的情況下，交替模式節能坡優化方案與人工設計方案運行能耗結果對比。本文能耗計算均采用自主開發的列車能耗計算軟件。

單位：m

表2 優化方案與人工設計方案結果對比

通過表2數據分析發現，在滿足線路縱斷面設計規范和運行工況約束條件下，通過遺傳優化算法得到的最優解在運行能耗上較原人工設計方案單向動車運行節能效果較為明顯，而運行時間偏差較小。

4.3 靈敏度分析

為了探究快慢車組合運營對于節能坡設計的影響，對不同快慢車運行比例、不同操縱模式下的節能坡方案進行優化求解并對節能效果進行比較。

4.3.1 交替模式運行能耗

由圖7可知，在不同快慢車比例的情況下，慢車與快車能耗都有很大程度的減少，減少最低13.8%，最高達到21.4%。隨著快車比例的增加和慢車比例的減少，慢車能耗增加，這是由于算法求解過程中更加側重于對快車的能耗優化所導致。但是在隨比例變化的過程中，慢車能耗變化幅度高于快車能耗變化幅度，因此認為，在快慢車組合運行條件下，慢車的節能效果比快車更明顯。

圖7 交替模式不同快慢車比例人工設計方案能耗與優化方案對比圖

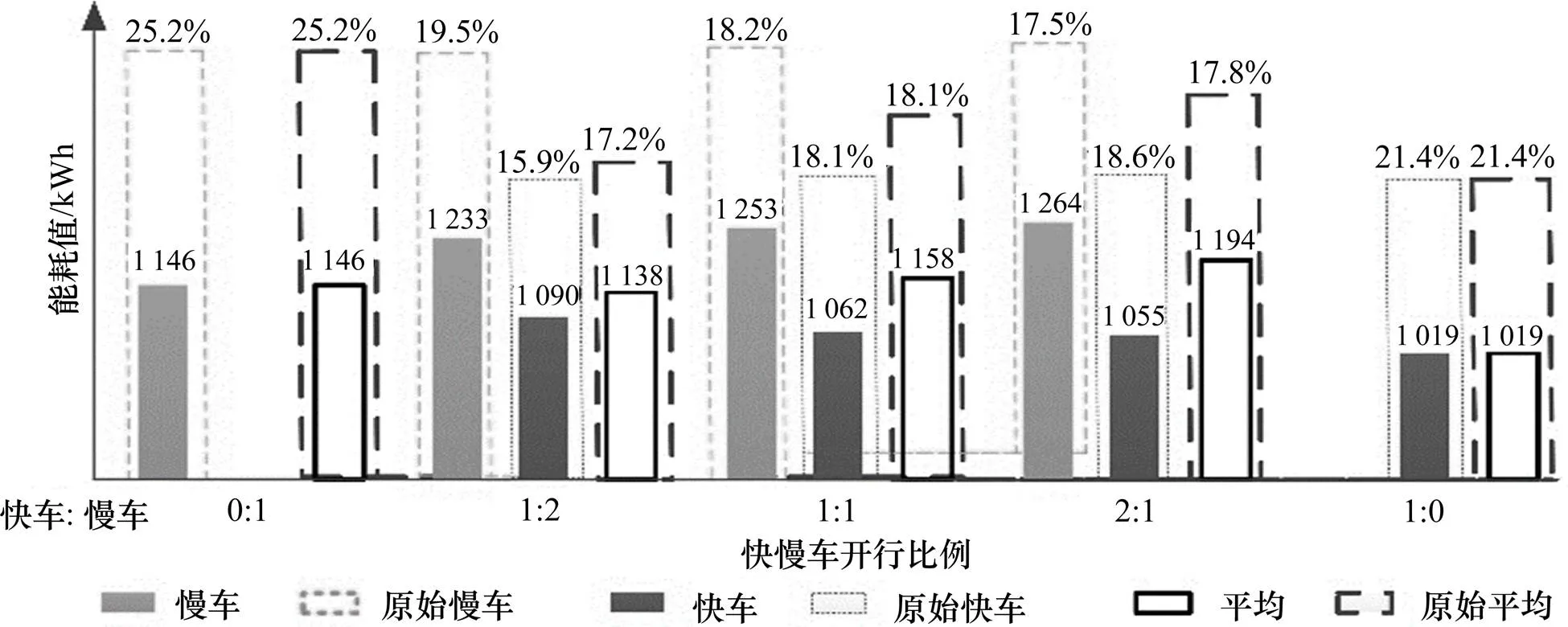
圖8 巡航模式不同快慢車比例人工設計方案能耗與優化方案對比圖

4.3.2 巡航模式運行能耗

巡航模式下，在不同快慢車比例的情況下，能耗減少比例都高于15.9%，說明本文提出的快慢車組合條件下節能坡設計優化模型及優化算法在2種不同運行模式下都能有效減少列車運行能耗，從而減少運營支出。不同比例下快車與慢車巡航模式能耗結果證明，慢車的節能效果比快車更明顯。

5 結論

1) 針對市域快線快慢車組合運行的特點，對線路節能坡優化問題進行定義，建立列車全線運行能耗和運行時間偏差的多目標優化模型，并設計基于改進遺傳算法的快速求解算法。以廣州地鐵18號線作為實證。結果表明本文所提模型與算法能夠高效求解節能坡方案，相對于原始方案，能耗降低了15.2%~25.2%，運行時間偏差低于2%，節能效果顯著且保證運行時效，具有可應用性。

2) 通過對仿真實驗結果的分析，認為交替模式與巡航模式下不同的快慢車比例對節能坡設計方案和節能效果有影響，慢車比例越大，節能坡方案的總能耗減少效果越顯著。

[1] 李忍相, 馮愛軍, 萬學紅. 北京市域快線主要技術指標研究[J]. 都市快軌交通, 2014, 27(3): 27?30. LI Renxiang, FENG Aijun, WAN Xuechong. Main technical indicators of Beijing regional express railway[J]. Urban Rapid Rail Transit, 2014, 27(3): 27?30.

[2] Kim D N, Schonfeld P. Benefits of dipped vertical alignments for rail transit routes[J]. Journal of Transportation Engineering-asce, 1997, 123(1): 20?27.

[3] CHENG W C, Schonfeld P. A method for optimizing the phased development of rail transit lines[J]. Urban Rail Transit, 2015, 1(4): 227?237.

[4] LAI X, Schonfeld P. Optimization of rail transit alignments considering vehicle dynamics[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012(2275): 77? 87.

[5] 呂希奎, 李永發, 孫培培. 高速鐵路進站節能坡設計方法研究[J]. 鐵道標準設計, 2016, 60(9): 42?48. Lü Xikui, LI Yongfa, SUN Peipei. Study on design of energy-saving slope in high-speed railway station[J]. Railway Standard Design, 2016, 60(9): 42?48.

[6] 陳進杰, 呂希奎. 高速鐵路區間節能坡設計方法研究[J]. 鐵道學報, 2013, 35(12): 83?89. CHEN Jinjie, Lü Xikui. Research on method of energy saving gradient design for high-speed railway sections[J]. Journal of the China Railway Society, 2013, 35(12): 83?89.

[7] Kim J H, Shin Y. Formulation and evaluation of railway optimal alignment design model[J]. Journal of the Korean Society of Civil Engineers, 2014, 34(6): 1845? 1850.

[8] Kim M, Schonfeld P, Kim E, et al. Comparison of vertical alignments for rail transit[J]. Journal of Transportation Engineering-asce, 2013, 139(2): 230?238.

[9] 張東欣. 列車牽引計算仿真系統的研究與開發[D]. 北京: 北京交通大學, 2016. ZHANG Dongxin, Research and development of the traction calculation simulation system for the rail train[D]. Beijing: Beijing Jiaotong University, 2016.

[10] 劉海東, 毛保華, 丁勇, 等. 城市軌道交通列車節能問題及方案研究[J]. 交通運輸系統工程與信息, 2007, 7(5): 68?73. LIU Haidong, MAO Baohua, DING Yong, et al. Train energy-saving scheme with evaluation in urban mass transit systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(5): 68?73.

[11] 樂建迪. 地鐵正線節能坡設計探討[J]. 鐵道標準設計, 2008(8): 17?19. LE Jiandi Discussion on the design of energy-saving slope for the subway main line[J]. Railway Standard Design, 2008(8): 17?19.

[12] TCCES2—2017, 市域快速軌道交通設計規范[S]. TCCES2—2017, Code for design of metropolitan rapid rail transit system[S].

Research on energy saving slope optimization model and algorithm of intercity railway under multiple-train line

CAO Jinmin, LI Dewei, DONG Xinlei, YU Jie

(School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

Most existing researches are limited to the optimization of energy saving slope of subway under the condition of stopping trains at each station. In order to solve the problem of energy saving slope optimization of urban rail transit express line of the sprinter and express combined operation trains, based on the stress analysis of the train, this paper proposed an energy consumption function of the sprinter and express combined operation trains and established the optimization model with the minimum operating energy consumption and the minimum deviation of the train running time. Then, according to the improved genetic algorithm, a solving algorithm was designed. Finally, the operation of Guangzhou express line 18 was applied as numerical examples to validate the performance of the proposed approach. Results show that the proposed approach can effectively solve the energy saving slope design problem. Compared with the original project, the optimization approach can reduce the energy consumption of train operation by 15.2%~25.2% while maintaining the small fluctuation of running time. This paper also finds that the different proportions of sprinter and express trains have effects on the energy-saving slope design scheme and energy saving effect. The greater the proportion of sprinter trains, the higher the energy-saving proportion of the total energy consumption is.

intercity railway; energy saving slope; genetic algorithm; combined operation of sprinter and express train

U212.34

A

1672 ? 7029(2020)03 ? 0756 ? 09

10.19713/j.cnki.43?1423/u.T20190574

2019?06?26

科技部重點研發計劃資助項目(2018YFB1201402)

李得偉(1982?)，男，青海樂都人，教授，博士，從事交通運輸規劃與管理研究；E?mail：lidw@bjtu.edu.cn

(編輯 蔣學東)