基于OMP算法的人口出生率影響因素分析
田 青
(西安財經大學統計學院 陜西 西安 710100)
一、引言
(一)研究背景
隨著信息技術的快速發展,每天都會產生大量的數據,如何有效地從中挖掘出有用的信息越來越受到人們的關注,傳統的數據處理技術已經無法滿足實際需要。因此,研究新的數據信號處理技術十分必要,很多學者也十分重視這個問題的研究。傳統的奈奎斯特(Nyquist)采樣定律要求采樣頻率必須大于原始信號最高頻率的2倍,這樣才能盡可能多的保留原始信號的信息,才能更高質量、高精確的進行信號無失真傳輸。而現代龐大數據量的信號,運用奈奎斯特定律進行采樣,將需要更大的存儲和傳輸代價。隨后Donoho[1]、Candes[2]等人提出了一種新型的信號處理技術——壓縮感知(CS)。壓縮感知技術不僅大幅地縮短了信號的處理時間,而且也大大降低了傳輸和存儲的成本。壓縮感知技術很好地解決了奈奎斯特采樣定律的限制問題,且效率更高。因此,壓縮感知在各領域都有很廣泛的應用。由于貪婪算法相對較快,受到學者們廣泛關注,本文將用貪婪算法中的OMP(正交匹配追蹤)算法對人口出生率的影響因素進行研究。
自21世紀以來,隨著計劃生育工作的開展,中國進入了低生育率水平。目前,我國人口結構發生了很大的轉變,勞動人口大幅減少,人口老齡化問題日益嚴重,這很不利于一個國家的可持續發展。在此情況下,我國逐步放開了計劃生育政策,并在2015年全面放開了二孩生育限制。然而,根據目前的結果來看,放開的計劃生育政策并沒有達到預想的結果。由此可知,目前我國的低生育水平受很多因素影響,因此,研究人口出生率的影響因素至關重要。
(二)研究現狀
CS理論在信號處理等多個領域得到了廣泛的應用。
目前,CS理論的發展主要涉及三個核心問題:稀疏表示、編碼測量和信號重構,其中重構算法是決定信號是否可以準確重構的關鍵步驟,因為重構算法決定了被恢復的信號在各項方面是否能滿足要求。CS重構算法的經典算法之一是基追蹤算法(Basis pursuit,BP)[3],它將l0極小化問題松弛為l1極小化問題,將非凸優化問題轉化為凸優化問題。貪婪算法也是重構算法一個很好的選擇,其中最優秀的一類算法是匹配追蹤(Matching pursuit)類算法,它是根據匹配追蹤(Matching pursuit,MP)算法延伸而來的[4],之后又有許多研究人員對其進行了更深的研究和改進,提出了正交匹配追蹤(Orthogonal matching pursuit,OMP)算法[5]。學者們將CS應用于人臉識別、語音識別、雷達定位、遙感成像等諸多領域,對其展開了廣泛的研究并取得了許多成果。
人口問題與經濟發展密切相關,是我國現階段面臨的重大問題之一。Friedlander和Silver(1967)[6]通過研究發現,每個國家在不同的發展階段,人口出生率與經濟增長變量具有不同的關系。彭浩然(2014)[7]認為,中國目前低出生率的轉變使得中國人口老齡化問題日益顯現。袁小平(2014)[8]等運用人口年齡結構系數及其對人口出生率變動影響的貢獻率指標證實人口年齡結構對出生率有顯著影響。向超(2016)[9]應用逐步回歸方法建立回歸模型,結果表明負擔少年系數、政府財政在教育醫療和社會保障方面的支出對人口出生率產生了顯著的影響。張煒和朱家明(2017)[10]采用ARIMA和二次指數平滑法對人口進行組合預測。華瑞和李雙亮(2018)[11]采用逐步回歸法和廣義差分法對模型的多重共線性和序列相關性進行修正,得出少兒撫養比與老年撫養比是影響人口出生率的主要因素。劉麗萍(2018)[12]采用Lasso回歸法探討影響人口出生率的因素,結果研究表明,國內生產總值、人均薪酬、少年兒童撫養比對人口出生率有明顯的正向影響。
除了這些已知的影響因素外,還有哪些因素影響著人口出生率呢?本文選取了20個影響因素,采用OMP算法,從多個方面來研究影響人口出生率的影響因素。
二、OMP算法的相關理論
(一)壓縮感知理論模型
假設有一個有限長的一維離散時間原始信號向量x∈RN,可以看作是一個N×1維的列向量,其本身就是稀疏的,非零元素的個數為K,即稀疏度為K(K?N),測量信號向量y∈RM的長度為M,Φ∈RM×N是(M×N(M?N))維的測量矩陣。測量信號向量y等于原始信號向量x乘以測量矩陣Φ,表達公式為:
y=Φx
(2.1)
壓縮感知的信號重建就是用已知的測量信號向量y和測量矩陣Φ來進行信號重建的過程,由式(2.1)可知,用M個方程可以解出N個未知數,因此我們可以通過求解一個最優化問題來重建信號。當滿足式(2.2)時,可以利用測量信號向量y和測量矩陣Φ很大概率上實現信號重建[13]。
M≥cKlog(N/K)?N
(2.2)
其中,c是一個極小值。
如果原始信號x∈RN不是稀疏的,但可以通過稀疏基變換將其轉化為另外一個域的稀疏信號,此時可以稱x在稀疏基域是稀疏的,即x通過由N個標準正交基構成的M×N維稀疏基矩陣Ψ變換到Ψ域,此時x可以表示為:
x=Ψs
(2.3)
此時s是x在Ψ域的表示向量,是一個長度為N的列向量,如果這里s是稀疏的,即非零元素的個數為K且K?N,則可以說x是一個在Ψ域上的K-稀疏信號。如今最常用的稀疏基主要有余弦變換基、小波變換基等。
則式(2.1)可以表示為:
y=Φx=ΦΨs=As
(2.4)
其中A=ΦΨ,是一個M×N維的矩陣,稱為恢復矩陣。這里要注意的是基矩陣可以是一個過完備字典也可以是一個原子庫[14],也就是說它可以是一個M×N(Z≥N)維的矩陣,這樣只要非稀疏信號在過完備字典或原子庫里可以稀疏表示即可。
根據式(2.4)、(2.1)可以發現,對本不是稀疏的原始信號x,同樣也可以通過本就是稀疏信號的重建方法來進行信號重建,即利用信號的重建算法重建出s,再用式(2.3)得到信號x。
(二)OMP算法的基本思想
OMP算法是基于貪婪算法的思想通過每次迭代選擇一個局部最優解來逐步逼近原始信號,基于MP算法的原子選擇準則來更新原子的支撐集,通過對原子集合正交化來保證迭代的最優性,進而減少到達收斂的迭代次數[44]。MP算法是最早的一種貪婪迭代算法,但由于每次迭代的結果可能不是最優的,而是次最優的。因此需要經過多次的迭代才能獲得最優的收斂結果。而OMP算法可以有效地解決這個問題,它沿用了MP算法中的原子選擇準則,在重建時每次迭代可以得到支撐集的一個原子,通過遞歸對已選擇的原子集合進行正交化來保證迭代的最優性,從而加快的收斂的速度并減少了迭代的次數。
OMP算法的基本思想是:以貪婪迭代的方法來確定傳感矩陣的列,保證在之后每次選取的列和現階段的冗余向量盡可能的接近,將采樣向量中的多余部分去除。在每次迭代時,計算當前殘差與觀測矩陣的內積,選取關聯度最大的一個原子,再加入索引集,更新殘差并判斷迭代次數。不斷重復上述過程,通過多次迭代保證該過程一直持續到迭代次數和稀疏度相同時,則迭代才停止。
(三)OMP算法的基本步驟
OMP算法的基本步驟如下:
輸入:傳感矩陣Φ∈Rm×n,采樣向量y∈Rm,稀疏度s;

初始化:殘差r0=y,索引集Λ0=φ,迭代計數t=1;
Step1:找到殘差r和傳感矩陣的列φj內積中的最大值所對應的腳標λ,即λt=argmaxj=1,…,N|
Step2:更新支撐集Λt=Λt-1∪{λt},記錄找到的傳感矩陣中的重建原子集合Φt=[Φt-1,φλt];
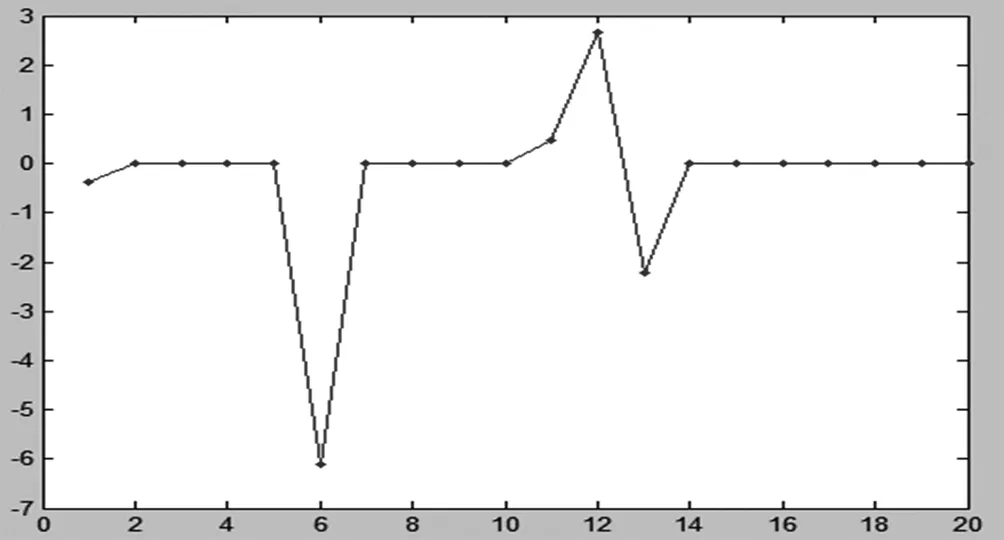
Step5:若t OMP算法的精確度雖不及BP算法,但它迭代次數少,運算復雜度低,是使用比較廣泛的一種重建算法,此算法需要在稀疏度已知的情況下使用。 本文使用的全國2007-2017年關于人口出生率影響因素的數據來源于中國統計年鑒。 人口出生率(Y)指一年內平均每一千人中出生的人數所占的比例。 出生率=(年出生人數/年平均人數)×1000% 選取人口死亡率(X1)、自然增長率(X2)、人口年齡結構0-14歲(X3)、人口年齡結構15-64歲(X4)、人口年齡結構65歲及以上(X5)、少兒撫養比(X6)、老年撫養比(X7)、嬰兒死亡率(X8)、國內生產總值(X9)、居民消費水平(X10)、離婚率(X11)、人均薪酬(X12)、居民消費價格指數(X13)、人均可支配收入(X14)、人均消費支出(X15)、孕產婦死亡率(X16)、社會固定資產在教育上的投資(X17)、商品房平均銷售價格(X18)、性別比(X19)、城鎮登記失業率(X20)。這20個涵蓋經濟發展情況、人口素質以及人口結構等方面的指標,以2007-2016年的數據為訓練集,再利用2017年的數據為測試集來驗證模型的精確度,以此來分析對人口出生率影響最大的是哪幾個因素。 首先對數據做預處理,對已有數據進行中心化和歸一化,去除量綱對回歸方程所帶來的影響。再用MATLAB軟件分別在稀疏度s為3,4和5時建立回歸模型。 表1 不同稀疏度下的回歸方程 根據MATLAB軟件計算出的在不同稀疏度下所生成的回歸方程及其對應的殘差(如表1所示),我們可以用2017年的數據進行模型驗證。 表2 OMP算法中稀疏度的選擇 由表2可知,稀疏度s=5時殘差最小,預測誤差最小,預測值最接近實際值。因此OMP算法所建立的模型為: y=-0.3690x1-6.1012x6+0.4664x11+2.6525x12-2.2258x13 其方程系數所對應的圖形如圖1所示。 圖1 模型系數圖 從OMP算法的回歸模型的估計結果可知,解釋變量人口死亡率(X1)、少兒撫養比(X6)、離婚率(X11)、人均薪酬(X12)和居民消費價格指數(X13)是影響人口出生率的幾個主要因素。其中人口死亡率、少兒撫養比和居民消費指數都是負向影響。X6、X12和X13對人口出生率的影響最明顯。 在我國,由于人口多、經濟發展不平衡,現階段人口老齡化情況日益嚴峻,人口出生率問題與經濟發展密切相關。本文選取了20個影響人口出生率的影響因素,采用OMP算法提取了其中影響最大的五個因素。研究結果表明,人口死亡率、少兒撫養比、離婚率、人均薪酬和居民消費價格指數是影響人口出生率最重要的幾個因素,其中少兒撫養比、人均薪酬和居民消費指數對人口出生率的影響最為明顯。
三、實證分析
(一)數據來源及指標選擇
(二)模型的建立


四、結論

