懸浮隧道車輛荷載響應分析與設計方法研究

鄒威，林巍 *

（1.中交懸浮隧道結構與設計方法研究攻關組，廣東 珠海 519000；2.中交公路規劃設計院有限公司，北京 100088）

1 概述

懸浮隧道車輛交通是基本荷載。當在水動力環境弱或無波、流環境建造懸浮隧道時，車輛荷載可能主控設計方案。車輛通過橋梁時產生沖擊力，兩者發生耦合振動[1]；相比橋梁，懸浮隧道沿程錨固豎向剛度可能更弱，浮筒式懸浮隧道車重由浮力變化平衡，錨索式懸浮隧道由部分管體凈浮力補償。

懸浮隧道交通荷載研究較少。文獻[2-3]提出考慮車重、路面不平整和波流因素的力-時程荷載模擬表達式，并借瓊洲海峽概念案例計算；文獻[4-5]等借上同案例，將水體作用簡化為管體橫向與豎向阻尼，分析張力腿豎向剛度、移動荷載大小、移動速度、行車間距對管體響應的影響；文獻[6]發現流固耦合效應增加動力放大系數，2D與3D模型在隧道受到強約束時較接近，且Morison方程較適用。文獻[4-6]均發現增強錨索剛度可減少動力放大系數。文獻[7]研究了錨索安全與振動穩定性、錨索材質、水阻尼與結構阻尼及錨索初張力對車輛荷載作用的影響。

本文提出了車速與懸浮隧道結構參數之間更系統的關聯，結合案例計算結果，擬合了動力放大系數與結構和車輛交通參數之間的表達式；并首次提出與分析了懸浮隧道車輛荷載扭轉問題。

2 懸浮隧道車輛動荷載響應分析

2.1 分析方法與計算模型

采用有限元軟件ANSYS建立懸浮隧道-車輛耦合分析模型（圖1）。管體采用Beam188梁單元，錨索采用COMBIN14彈簧單元；車輛采用MASS21質量單元和COMBIN14彈簧單元分別模擬單輛車的質量和其減震系統。

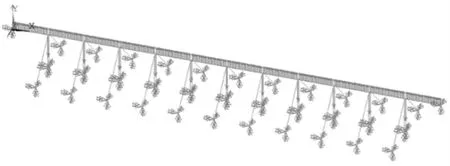
圖1 懸浮隧道模型外部荷載及約束條件Fig.1 External load and constraint conditionsof the SFT model

基準計算工況模型參數。懸浮隧道管體長度L=1 200 m；橫斷面簡化為圓環形狀，外徑12.8 m，內徑10.8 m；鋼筋混凝土彈性模量E=3.6×1010Pa；管體質量連其附加水質量223 000 kg/m；縱向布纜間距h=100 m；單個斷面纜索合計豎向剛度k=9.4×106N/m。車輛速度v=10 m/s；車輛重量m=2 000 kg；減震系統剛度K=1.0×1020N/m。

懸浮隧道和車輛耦合計算是通過有限元動力逐步法完成，即通過強制位移（D）將車輛單元移動到管體位置對應的梁單元相應的節點，再通過耦合（CP）將車輛節點與管體梁單元節點通過彈簧連接。計算完成后，刪除上述耦合關系（CPDELE），進入下個計算時間步[8]，重復循環。

2.2 工況

懸浮隧道車輛動荷載響應的車輛影響因素有：車速、車重、自身剛度、車間距等；隧道影響因素有：管體長度、質量、抗彎剛度、錨索剛度和布置等。分析其中部分關鍵因素見表1。研究：1）單輛車勻速通過懸浮隧道時引起管體跨中撓度與其靜止停在管體跨中引起的靜撓度的比值，后文稱為動力放大系數μ；2）不同間距車隊通過懸浮隧道時引起的管體跨中垂向最大加速度。

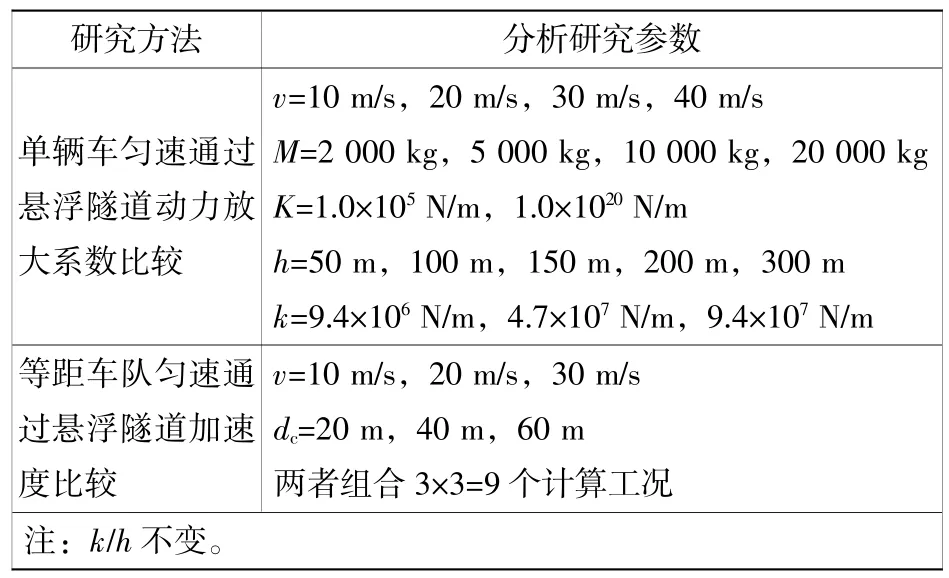
表1 懸浮隧道-車輛耦合模型分析參數工況表Table1 Analysisparametersof SFT-vehicle interaction model

2.3 結果

圖2是單輛車不同速度駛過隧道時隧道跨中撓度w時程。圖3為不同錨索豎向剛度k時動力系數μ隨車速變化。可見隨車速增加，動力系數基本呈增加趨勢。車速相同時，錨索剛度越大，動力系數越小，且車速越快時該趨勢越明顯。

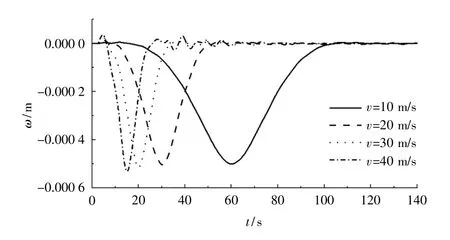
圖2 不同車速下隧道跨中撓度時程Fig.2 Deflection history of the mid-span section under different vehicle velocity

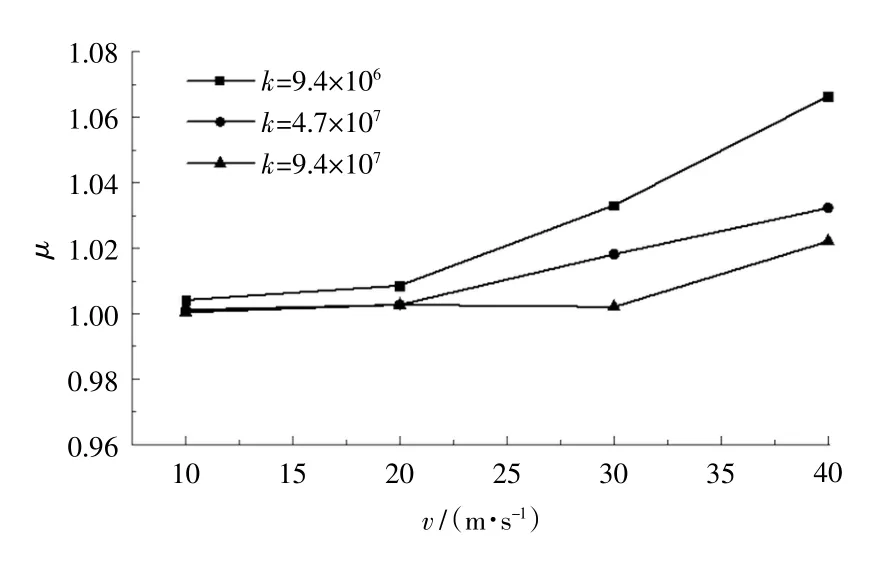
圖3 動力系數μ關于車速v的變化Fig.3 Dynamic coefficientμvarieswith respect to velocity v

其它計算結果概述。1）車輛質量m對動力放大系數影響很小，隧道跨中撓度最大值與車輛質量呈近似線性同向關系，可能因為車輛質量相較于懸浮隧道質量較小。2）布纜間距h改變時，除去間距最大h=300 m工況，其它結果動力系數相同。3）車輛剛度K改變時，對計算結果基本無影響，這可能因為單輛車對隧道作用較小，且本文不研究常規的路面起伏問題。

圖4 不同車速或車距跨中加速度時程Fig.4 Acceleration time history of the mid-span section under different vehicle velocity or vehicledistance

圖4 是隧道跨中加速度時程計算結果。圖5是最大加速度與車速和車距的關系。

可見，1）本研究計算模型車輛對懸浮隧道加速度（舒適性設計）影響小，基本可忽略；2）隨著車速增加或車距減小，懸浮隧道跨中加速度增幅較大。

圖5 跨中最大加速度與車速和車距的關系Fig.5 Relation between the maximum acceleration of mid-span section with vehiclevelocity and varied spacing

2.4 動力放大系數通用公式擬合研究

研究指出沖擊系數與車速和結構自身基頻有關[9]，規范也有推薦值[10]。本文進一步指出動力放大系數與該車過隧道的時長（假設平均行駛）和隧道縱面一階自振周期比值存在直接關聯。也即：μ=f（L/（Tv））（1）式中：L為隧道長度；v為車速；L/v也即車過隧道時間；T為結構縱垂面內一階自振周期。

借2.3節計算結果，擬合式（1），得到式（2），見圖6。相關系數R2=0.91。由圖可知，當L/（Tv）值較大時，動力系數μ趨近于1。

假定隧道管體兩端完全固結，T的計算表達通式見式（3）：

式中：m為隧道管體延米質量；k0為延米剛度；β與約束方式有關，例如固結時為4.73。

將式（3）代入式（2），得到式（4）：

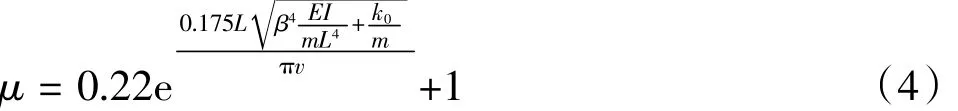
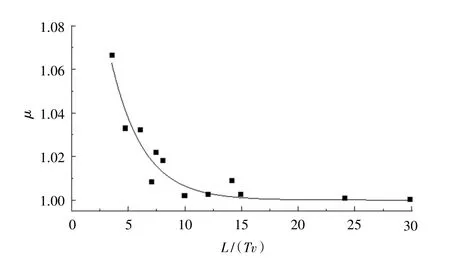
圖6 動力系數μ與L/（Tv）關系Fig.6 Relation between dynamic coefficientμand L/（Tv）

3 車輛荷載下懸浮隧道的抗扭評價

3.1 扭轉平衡數學模型

本文首次提出車輛在懸浮隧道管體內一側停靠或行駛而導致的管體扭轉問題并在此初步研究。

基于彈性地基梁假設[11]，建立沿著懸浮隧道管體的扭轉平衡方程，將懸浮隧道錨固系統簡化為等效扭轉連續彈簧，計算模型見圖7。建立等效彈性基礎下懸浮隧道扭轉平衡方程（5），假設兩端完全固結，方程邊界條件見式（6）。解方程得到管體在單側均布的車輛荷載作用下的沿程扭轉角（包含跨中最大扭轉角φmax）。

式中：φ為扭轉角；x為隧道里程；G為剪切彈性模量；I為極慣性矩；r為錨索繞扭轉中心的力臂；為延米剛度；截面扭轉非常微小情況下-為錨固系統提供的延米力矩；GI用于估算管體扭轉產生的扭力；GI則為微元管段前、后截面的延米力矩差；qk為車輛均布荷載；l為車輛荷載距扭轉中心的距離。

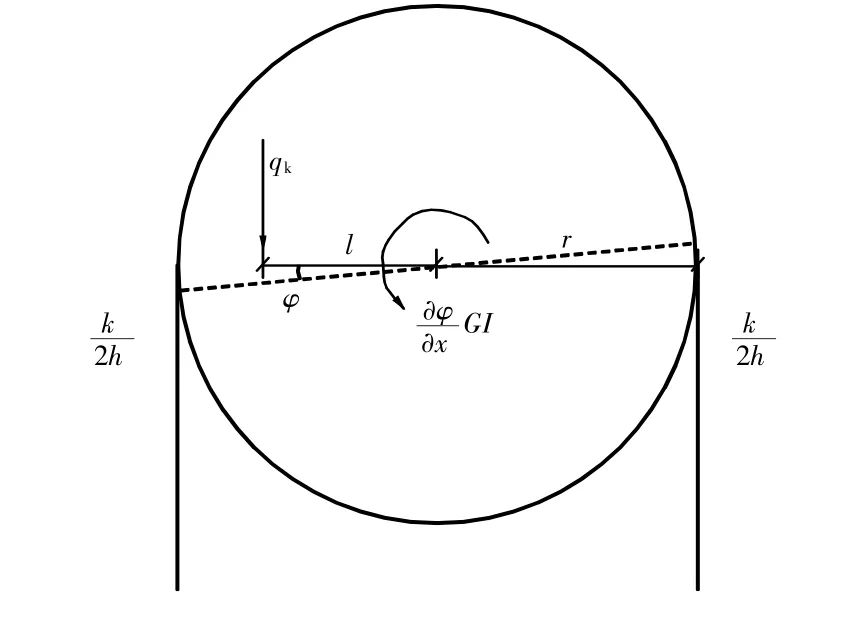
圖7 截面扭轉平衡示意Fig.7 The sketch of the SFT cross-section atthe equilibrium

用建立的模型計算隧道管體沿程扭轉角。結果見圖8。可知，懸浮隧道橫截面的最大扭轉角出現在跨中，且隨隧道長度增加而增大。但當隧道很長時，例如本算例L=30 000 m時，因沿程錨固系統抗扭力矩與車輛荷載的力矩平衡，跨中附近扭轉角基本不變。此時方程（5）代表管體相對扭轉的高階項GI可忽略，簡化后跨中的扭轉角

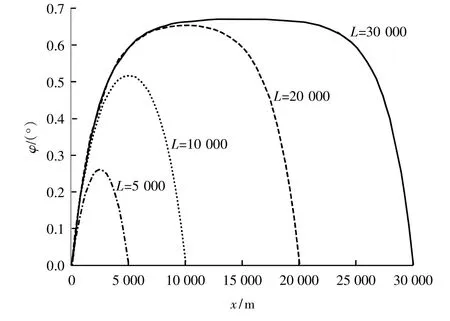
圖8 不同長度懸浮隧道截面扭轉角的沿軸向變化Fig.8 The cross-section torsion angle of different long SFT varies along the axial direction

3.2 扭轉角工程影響評估

假設設計準則為管體撓度不大于L/500或截面最大扭轉角不大于0.5°。比較前文算例在懸浮隧道兩個車道滿布車輛均勻荷載和單個車道滿布時結構的撓度和轉角。取L=600 m、1 200 m、2 400 m、5 000 m隧道，結果見表2。可見，隧道較長時截面最大轉角很可能成為隧道設計控制工況，且車輛單側通行的情況在現實中也較為常見。

表2 不同長度隧道跨中撓度和轉角比較Table2 The comparison of mid-span deflection and rotation of different long SFT

3.3 懸浮隧道管體橫斷面抗扭能力綜合評價

懸浮隧道管體橫斷面已有多種概念方案[12]，圖9中，截面1～截面2與截面3～截面5分別為擬定的2車道和4車道懸浮隧道典型橫斷面。采用3.1節建立的方法計算不同橫斷面在單車道滿布車輛均勻荷載時的最大扭轉角并比較。計算參數及結果總結見表3。可見：1）盡管橫斷面較寬斷面的車輛荷載力臂大，其扭矩大，但是其結構抗扭能力和錨固系統的力臂也大，抗扭剛度相應增強，斷面綜合抗扭能力需計算確定；2）當隧道很長時，錨固系統抗扭剛度是主控項，斷面綜合抗扭能力取決于；3）當隧道較短時，橫斷面結構抗扭剛度是主控項，斷面綜合抗扭能力取決于；4）就當前計算模型，懸浮隧道管體寬分離式橫斷面對于單側車輛荷載工況適應性最佳。

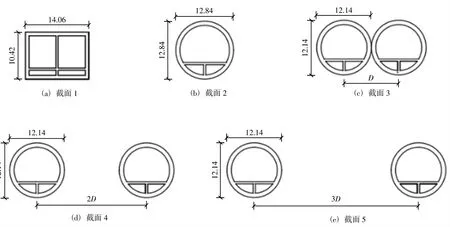
圖9 5種不同形式懸浮隧道截面Fig.9 Five different typescross-section of SFT

表3 不同形式截面懸浮隧道最大扭轉計算比較Table3 The comparison of maximum torsion angle of the SFT with different sections

4 結論與展望

本文提出移動車輛荷載的動力放大系數與車過隧道時長的直接關聯，后者的效用類似循環荷載頻率與結構基頻之比。對于本研究算例，車輛荷載對懸浮隧道加速度影響很小，車速增加或車距減小時跨中加速度明顯增加，但引起的管體加速度值相比人體能感知到的量級（如0.5 m/s）基本可忽略。車輛單側行駛導致的隧道扭轉問題不應忽略，可能成為結構設計控制工況。不同橫斷面過車抗扭效應取決于錨索布置、車道位置、結構抗扭剛度，所以應進行詳細分析比選。

需進一步研究問題：1）基于實測數據的非理想等間距車譜作用下懸浮隧道響應研究；2）單向交通過隧道時（例如水體兩端分別是住宅區和辦公區，上班時段車輛僅從隧道一端到另一端，下班時相反）引起的扭轉加速度研究。

未來，無人駕駛可能將改變傳統對隧道內車速和車間距及車重分布密度的認知，分析方法需要重新評估。