?鄧州市糧食產量模型的建立和分析

楊晉

隨著經濟社會的快速發展和土壤環境污染、工業占用耕地等因素的存在，糧食生產的形勢嚴峻而迫切，給糧食安全帶來了一定的挑戰。本文以鄧州市為參考，運用SPSS軟件通過多元線性回歸的方法，初步建立鄧州市糧食產量模型并分析其影響因素，為相關部門進行糧食產量方面的研究提供參考價值和理論依據。

一、數據準備

從表1（數據來源《鄧州統計年鑒》）可以看出，2004—2015年全市糧食播種面積、農田有效灌溉面積、糧食產量均呈逐年增加的趨勢;單位面積產量出現一定程度的波動;鄉村從業人數增加至2010年出現峰值，然后下降;化肥施用量基本呈增加趨勢。因此，擬初步建立鄧州市糧食產量和各影響因素之間的多元線性回歸模型，假設糧食產量為因變量y，糧食作物面積、單位面積產量、鄉村從業人數、農田有效灌溉面積、化肥施用量分別為自變量x1、x2、x3、x4、x5，因變量和自變量之間存在線性關系。

二、數據分析

（一）對因變量y進行正態性檢驗

打開SPSS軟件，選擇菜單分析（A）—描述統計（E）—探索（E），將y選入因變量列表，繪圖（T）選擇待檢驗的正態圖，對因變量y進行正態性檢驗。

從表2輸出結果得到正態性檢驗有兩種方法，KS檢驗法和SW檢驗法。因樣本量為12個，小樣本適用SW檢驗法，即統計量0.899，顯著水平sig.=0.155>0.05，因此因變量y符合正態分布，可進一步進行回歸分析。

（二）因變量y與自變量x1的回歸分析

選擇逐步回歸分析法，主要是為了排除自變量過多產生的干擾，有利于在自變量之間選擇出最佳的回歸方程。從表3可知：

1.由逐步回歸法得出的模型2，剔除了自變量x3、x4、x5的影響，自變量x3、x4、x5與因變量之間不存在顯著性差異;而留下的自變量x1、x2偏回歸系數的顯著性均 <0.05，與因變量之間存在顯著性差異。

2. 通過運算過程中得出自變量x1、x2的方差膨脹因子（VIF值）均<5，可認為變量之間不存在多重共線性，模型2成立。

3.根據常量B0為-92.038，糧食作物面積x1的系數為0.543，單位面積產量x2的系數為0.017，糧食產量y與糧食作物面積x1、單位面積產量x2的回歸方程

可表達為：

y= -92.038+0.543x1+0.017x2

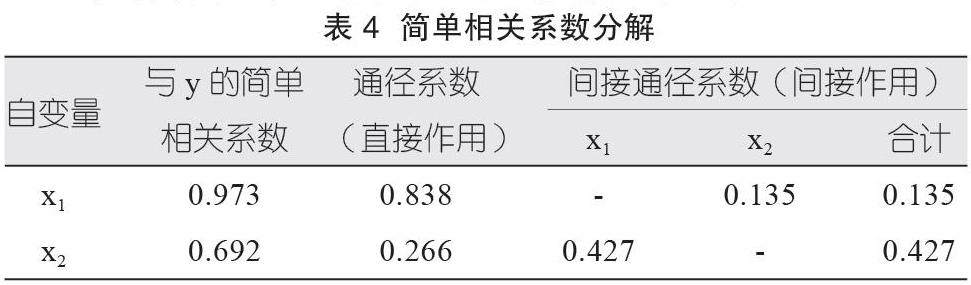
4.直接得出通徑系數，即自變量x1、x2對因變量y的直接作用分別是P1y=0.838、P2y=0.266。

（三）計算間接通徑系數

從皮爾森相關系數輸出結果得到自變量與因變量、各自變量間的相關系數。自變量與因變量之間的簡單相關系數分別是r1y=0.973、r2y=0.692;各自變量間的相關系數r12=r21=0.509。

x1通過x2對y的間接通徑系數分別為：r12×P2y=0.509×0.266=0.135。x2通過x1對y的間接通徑系數分別為：r12×P1y=0.509×0.838=0.427。同時，簡單相關系數的值等于通徑系數直接作用和間接作用之和，符合統計理論值。整理數據見表4。

三、小結和討論

（一）在自變量對因變量y的直接影響下，糧食作物面積x1對糧食產量y的影響程度最大，然后是單位面積產量x2。在自變量對因變量y的間接影響下，單位面積產量x2對糧食產量y的影響程度最大，然后是糧食作物面積x1。說明該模型下糧食作物面積和單位面積產量都是影響糧食產量的主要因素。

（二）通過SPSS軟件對數據進行統計分析具有專業性、便捷性、可靠性的特點，其輸出的結果一目了然，與理論值一致。因此，SPSS軟件進行統計分析有一定的推廣和應用價值。

（三）該模型下可以得出，要想確保糧食產量的穩定發展，不僅要穩定播種面積、提高單位面積產量，還要加強農業基礎設施建設，充分利用好丹江水資源的有效配給，提高農田有效灌溉面積，為鄧州市的糧食穩產增產保駕護航。除了以上主要因素，還有環境、氣象、農業良種良法配套、農業機械化程度、災害發生情況等因素也在不同程度上影響著糧食產量，因此，這些因素有待進一步驗證。