基于T-prim模型的肺氣管分割算法

石躍祥 杜 祎

(湘潭大學 湖南 湘潭 411105)

0 引 言

肺部疾病已成為世界范圍內人類發病率和死亡率提升的主要原因之一，其影響預計將在未來20年內增加，屆時它將成為第三大死亡原因和第五大發病原因[1]。而針對肺部疾病的治療必須基于科學高效的現代醫學技術，只有這樣患者才可以從治療中獲益。醫學圖像解釋和決策被認為是診斷放射學中最重要的過程[3]。為了幫助放射科醫生進行圖像解釋，醫學圖像的計算機分析最近已在臨床上實施，分割出肺氣管樹的形態可以作為指導醫生針對病理過程進行治療觀察的標簽[5]，從而針對病灶不同階段的過渡治療與檢測會變得更加準確而高效。而圖像分割是研究人員面臨的經典難題之一。

隨著醫學影像學的發展，圖像分割在醫學應用中起著重要的作用。為了取得這些研究的成果，精確地分割出肺氣管樹是不可缺少的。然而，對位于肺氣管樹末端更細小、更高級的氣管進行分割是很困難的。Thorsten等[2]提出的同步肺氣管分割和重建方法在分割階段執行了骨架算法，從而有助于防止在快速行進生長過程漏入肺實質。數學形態學方法使用一系列的形態學結構元素進行分割[6]。Francoise等[4]結合形態濾波、連接樣本標記和條件分水嶺算法對支氣管進行分割。有一種基于增強管狀結構的肺氣管樹識別策略表現更為優異。Aykac等[7]首先利用核尺寸增大的形態閉合操作進行二維灰度氣道重建，然后采用迭代閉合和擴張操作獲得所有潛在肺氣管，最后采用前后連通的三維形態重建抑制噪聲，分割出完整的肺氣管樹。Saba等[8]使用肺氣管樹的三維模型和掃描儀的點擴散函數進行了二維測量，與半波寬(FWHM)算法[9]相比，獲得了更好的內邊界亞像素精度，在針對外氣管壁邊界的比較實驗中也取得了更好的效果[11]。Preteux等[10]使用多項式估算肺氣管內壁位置，但會使細支氣管的分割誤差大大增加。Kerschnitzki等[11]根據輸入圖像與氣管和氣管壁兩個標志物之間強度的相似性，為每個體素分配一個模糊成員。該算法允許兩個區域相互競爭，從而決定了所有體素的類標簽。模糊連通性也可用于肺血管分割。Naqibullah等[15]提出了一種基于形態學的人工肺氣管樹分割方案，該方案基于模糊連通性(FC)方法來抑制進入周圍區域泄漏。這些方法在分割過程中保留了支氣管分支的圓柱形特征，在六代支氣管之內能夠檢測到更多的分支。雖然這一過程可以進一步幫助識別細小支氣管的位置，但也會在肺部區域產生難以避免的假陽性現象。Charbonnier等[13]采用深度學習法的方法分割肺氣管，使用深度神經網絡提取特征值，用于查找泄漏并通過調整網絡參數以消除分割過程中的泄漏，但計算成本非常高。

由于肺氣管結構固有的復雜性以及CT圖像分辨率的局限性，大多數肺氣管分割方法對主氣管和一些明顯的支氣管的分割是有效的[9]。這些算法通常依賴于CT上氣道的外觀(二維的暗橢圓形狀等)，或者基于一些預先定義的基于解剖的規則來控制分割過程。然而，這些規則和假設在噪聲、人工干預，或氣管病變的存在下可能是不準確的。對于高階的細小支氣管，迫切需要一種分割方法來精確地分割出肺氣管樹。

本文的創新點在于：(1) 對分水嶺算法分割框架進行了優化，并在馬爾可夫隨機場的角度對優化分割框架進行了進一步的修改，可用于從多個對象背景分割出特定的類。(2) 對prim最小生成樹算法進行改進，提出一種T-prim模型。根據以上優化框架得到的最優能量函數構建了評價支氣管灰度數據的可信度評價標準，以此結果作為閾值執行MST算法獲得完整的肺氣管樹結構。通過與EXACT09競賽算法的效果作對比驗證了本文算法能夠快速準確地分割出完整的肺部氣管樹，在整個過程中幾乎不會出現泄露誤分割等現象。

1 馬爾可夫場角度下的分水嶺算法分割框架優化

1.1 分水嶺算法的優化分割框架

文獻[14]提供了一個通用的分割方案，該框架可以提供利用種子節點進行分割的算法，可以對該框架進行進一步擴展。本文取其中分水嶺最小生成樹算法作為一個特殊的案例進行優化使用。通過將該算法應用于肺氣管樹分割環境，對該類分水嶺分割模型進行了具體化改進。

將無向圖定義為Go=(Vo,Eo)，帶有節點集Vo以及邊界集Eo，其中Eo?Vo×Vo，基數n=|Vo|,m=|Eo|。vi和eij分別代表Vo、Eo中的節點和邊界。由圖像灰度生成權重值，對wij做如下設置：

wij=exp(-β(▽I)2)

(1)

式中：▽I為圖像I的歸一化梯度，灰度圖像的梯度為Ii-Ij，假設權重為非負，wij為邊界eij的權重。廣義能量由下式給出：

(2)

式中：y表示測量配置，x表示目標配置；wij為目標配置梯度的權重。

假設G為一個無向圖，則wij=wji。該兩類分割圖優化方法框架為：

Step1

(3)

s.t.x(F)=1,x(B)=0

Step2

(4)

式中：xi、si分別代表節點vi的背景概率以及結果標簽。x是Vo中所有節點的概率集合。至此將框架擴展到分水嶺算法領域。

1.2 馬爾可夫隨機場角度的能量最小化框架

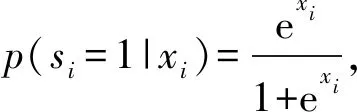
p(si=1|xi)=max{min{xi,1},0}=

(5)

若輔助節點的值介于0和1之間，則當權重均為正值時，取其值介于0和1之間。因此可以使用p(si=1|xi)=xi，不必擔心xi在[0,1]之外。

在圖像數據I中推斷隱含變量xi。通過后驗模型，可以在貝葉斯框架中估計出隱含變量。

p(x,s|I)∝p(x)p(s|x)p(I/s)=

(6)

模型p(x)中，伯努利變量的參數在空間上不斷變化。平滑處理后，空間先驗概率參數初始化為：

(7)

式中：λ>0，權值為正值。可以估算出邊緣化映射準則：

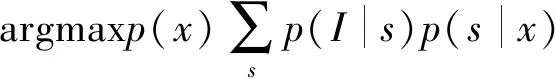
(8)

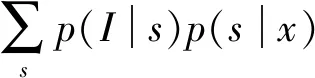
(9)

式中：wi0≥0，wi1≥0，可將參數xi糾正到0和1之間。通過設置種子節點vi的權重(wi0,wi1)=(0,∞)，背景節點權重(wi0,wi1)=(∞,0)。參數化之后，圖像估計值可轉化為求式(5)中能量函數最小化問題。詳細過程為：

p(x,y|I)∝p(y|x,I)p(x|I)=p(y|x)p(x|I)=

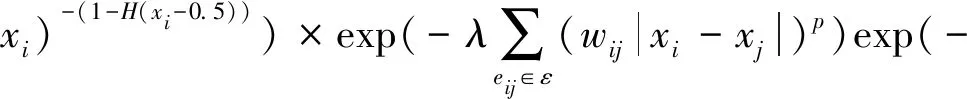
(10)

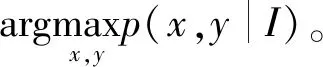
(11)

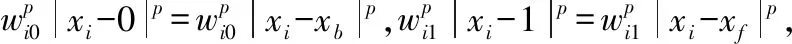
(12)

如果p=∞，集合ε包含模型(11)，通過p范數使E(x)參數化：

(13)

2 T-prim模型

2.1 模型構建

T-prim模型的構建方式與經典的prim最小生成樹的節點生成方式相似。其中一個主要的改進是prim算法需要到達圖中的所有節點，但在本文算法中，如果堆棧中沒有符合權值條件(Ts≥τ)的對象節點，則這些節點不會被納入最小生成樹。而且，prim樹的生成可以看作是一階馬爾可夫過程，用于以最小邊緣添加節點來構建樹的結構。因此T-prim模型可使用在上一節的優化分割框架中。在該算法中，執行的目標是在樹中添加具有最大加權和管狀結構分數(Ts)的節點。如圖1所示。

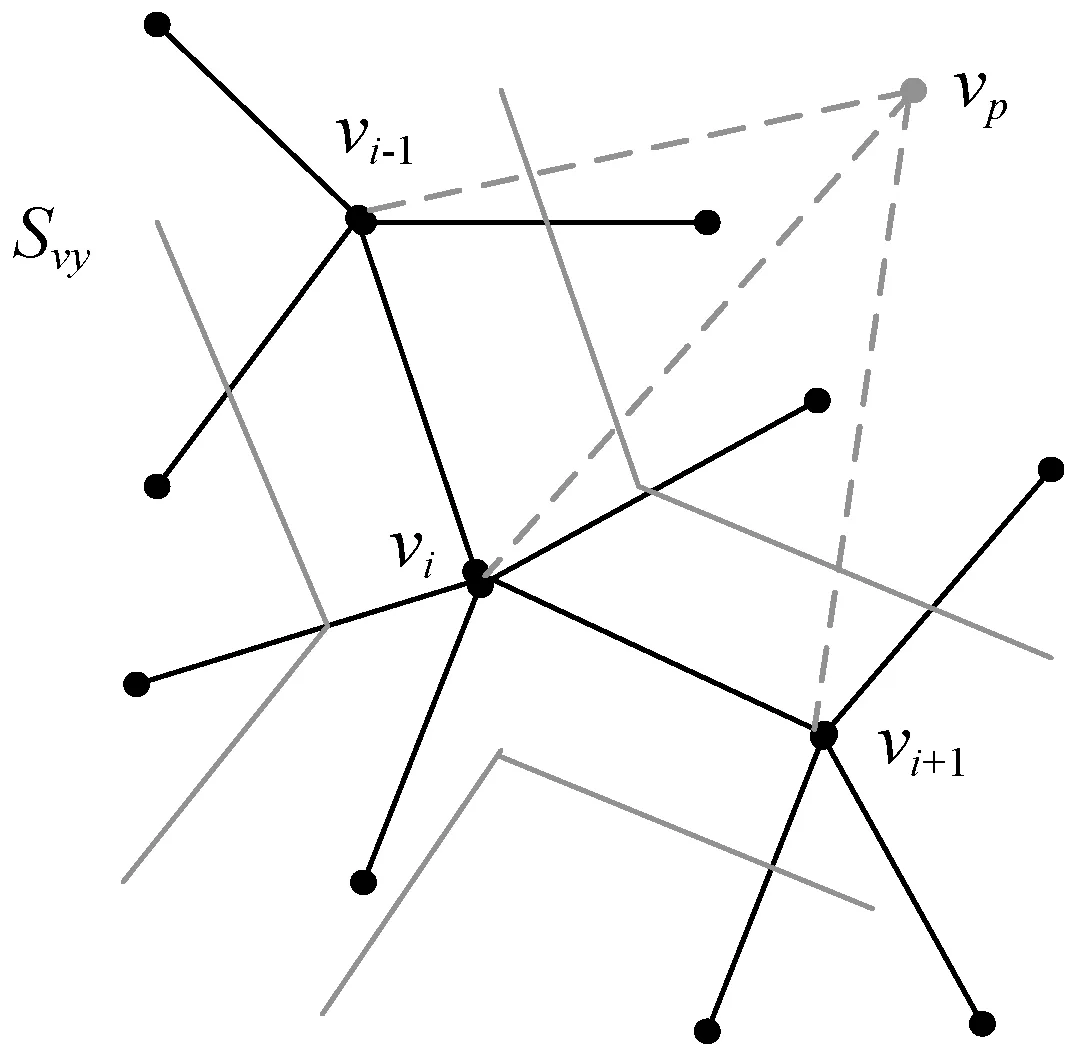
圖1 T-prim構造圖

圖1中，vi∈VT-prim。vp是用于實現的虛擬圖形節點。e(vp,VT-prim)表示所有邊緣集，包括連接節點vp和VT-prim中的節點的所有邊緣。這些邊緣用圖中的虛線表示。e(vp,Svy)代表所有連接vp和肺氣管種子節點的邊緣。最終構造的圖形包括兩部分：圖像網格(Go)和T-prim部分(G′)(虛線和關聯節點)。

當確定一個種子節點之后，憑借與管狀結構權值的極大值評分(Ts)來迭代添加節點，直到T-prim被構建起來。在實際應用中，樹形結構會非常稠密，尤其是在細小的支氣管區域中。根節點和氣管以外節點的路徑上可能存在許多節點。管狀結構評分(Ts)的計算是非常重要的部分。Ts計算方式如下：

Ts(vi)=λ×Ts(vi-1)+(1-λ)×mf(vi,di)=

(14)

式中：di=vi-vi-1。當i=1時，則：

(15)

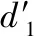
(16)

(17)

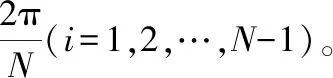
2.2 優化分割框架的使用

與二維圖像相比，三維圖像的分割任務顯得更加重要和困難。對于肺氣管樹分割，由上一節可知，優化框架可以修改為以下目標函數：

(18)

s.t.x(SV)=1,x(SB)=0

最小生成樹模型T-prim=(ET-prim,VT-prim)中包含邊界集合ET-prim和節點集合VT-prim。Twi為節點vi∈VT-prim的T-prim管狀結構響應。SV和SB代表肺氣管種子集合和背景區域種子集合。在這個目標函數中，所做改動刪除了前景和背景的原始區域能量項，并為集合中的節點添加了一個新的集合VT-prim，來衡量肺氣管數據的可信度。

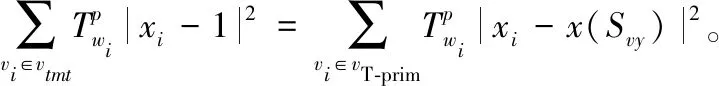
(19)

s.t.x(SV)=1,x(SB)=0

這樣對該目標函數使用上一節優化的功率分水嶺框架構造出圖結構，完成分割。總體過程梳理為下：

輸入為圖像數據像素集I，肺氣管種子節點SV,背景區域節點SB。在圖像I中，Eo為連接相鄰像素邊緣的集合，Vo為肺氣管壁的像素集合。計算權值的參數為w，定義Go=(Vo,Eo)計算權值wo={wij=exp(-(Ii-Ij)2/(2w2))}。得到maxw=max{wij∈wo}。執行上一節所述過程，利用I、SV以及maxw獲得T-prim和Tw。由定義可知G′=(V′,E′)，其中V′=vp∪Vtp∪Svy，E′=e(vp,Sv)∪e(vp,Vtp)。則：

W′(e(vp,Sv))=maxw

(20)

W′(e(vp,Vtp))=Tw(Vtp)

(21)

令G=Go∪G′,W=Wo∪W′,將G輸入上一節馬爾可夫隨機場角度優化的分水嶺分割框架，得到X,即為輸出。

2.3 總體分割過程

本文采用三維混合方法完成肺氣管樹的分割。包括三維形態重建、T-prim模型和區域生長，優化的分水嶺算法框架。

首先通過三維形態重建和區域生長算法的靈活運用，獲得肺主氣管。之后改進prim算法構造T-prim模型，T-prim模型提供了良好的數據可信度權值，并進行了初步的圖形構建。然后利用優化的分水嶺分割算法通過分割目標函數的能量函數優化結果構造了完整的圖，最大程度避免滲漏，從而獲得細支氣管。這里的關鍵思想是，不僅基于單個體素的像素，而且基于來自周圍環境的信息來決定區域的增長。

具體地說，在主氣管骨架提取的基礎上，可以自動獲取T-prim的初始種子點，然后通過其算法的迭代過程生成T-prim中的節點。當T-prim建模在肺葉支氣管中完成，利用優化分割框架細支氣管可以有效地分割出來，并且極少出現泄露問題。分割框架如圖2所示。

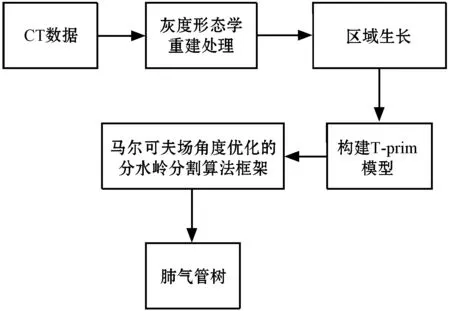
圖2 分割框架

至此完成算法分割過程。本文算法的創新主要在于：在肺氣管分割領域對prim最小生成樹算法進行改進，引入構建T-prim模型。對原有的分水嶺分割框架從馬爾可夫鏈角度進行擴展優化，使其適用于T-prim模型構造，利用T-prim構造新目標函數，對新的能量函數進行優化完成對細支氣管的分割。

3 實驗與分析

為了驗證本算法的有效性，這里給出了本文算法在EXACT09競賽后20例測試數據中的分割結果，并用其標準進行評估，這是國際公認的肺氣管分割參考標準。

3.1 肺氣管分割結果展示

本實驗結果均在VS2015與MITK平臺上得到。競賽中的40例數據中，前20例數據供參賽算法用來進行實驗或作為訓練集。后20例數據集用作算法的測試。這些測試數據包含一套完全獨立的異質性掃描，包括不同重建核的吸氣和呼氣掃描，以及不同程度的間質性肺病[12]。使用這一個公共數據集可以直接比較不同方法。圖3為本文算法的分割結果。

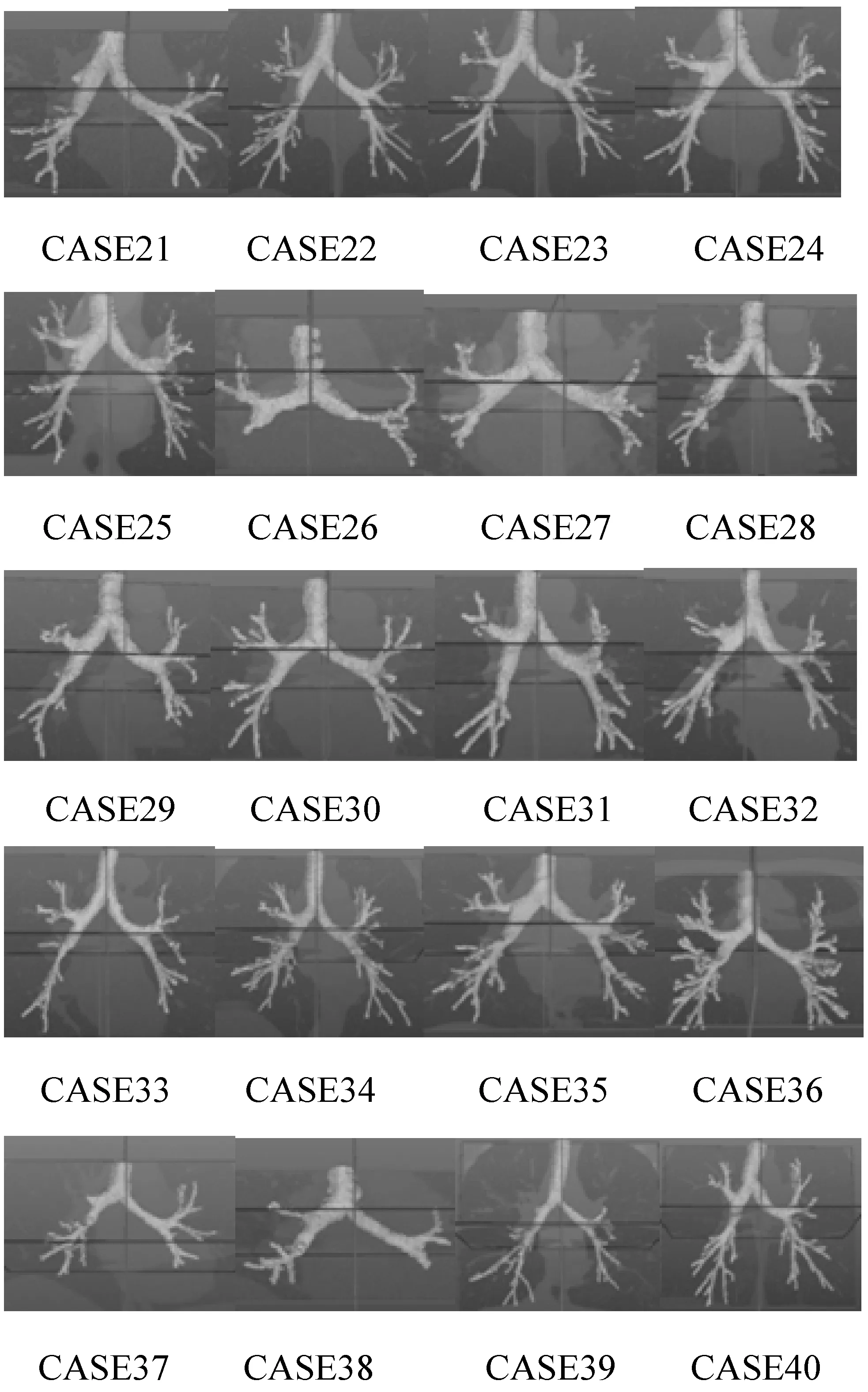
圖3 三維重建算法分割結果展示

3.2 與兩種EXACT09算法的對比實驗

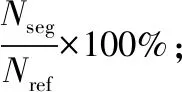
將本文算法與EXACT09競賽中Weinherimer等以及Wiemker等提出的算法進行對比。兩者算法均有采用過基于圖形構造的方法，與本文算法有一定的可比性，存在一定的競爭對比關系。對比結果如圖4-圖6所示。

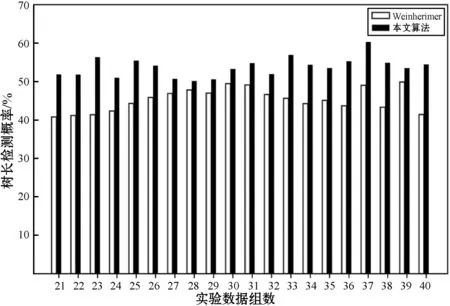
(a) 與Weinherimer等分割結果對比

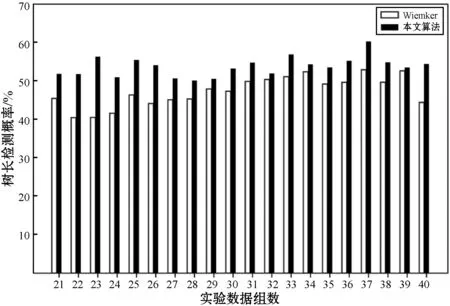
(b) 與Wiemker等分割結果對比圖4 正確檢測樹長與檢測樹總長比值對比圖

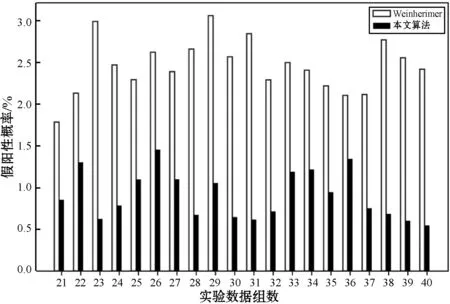
(a) 與Weinherimer等分割結果對比

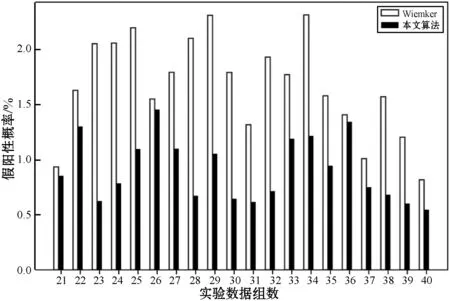
(b) 與Wiemker等分割結果對比圖5 假陽性對比圖

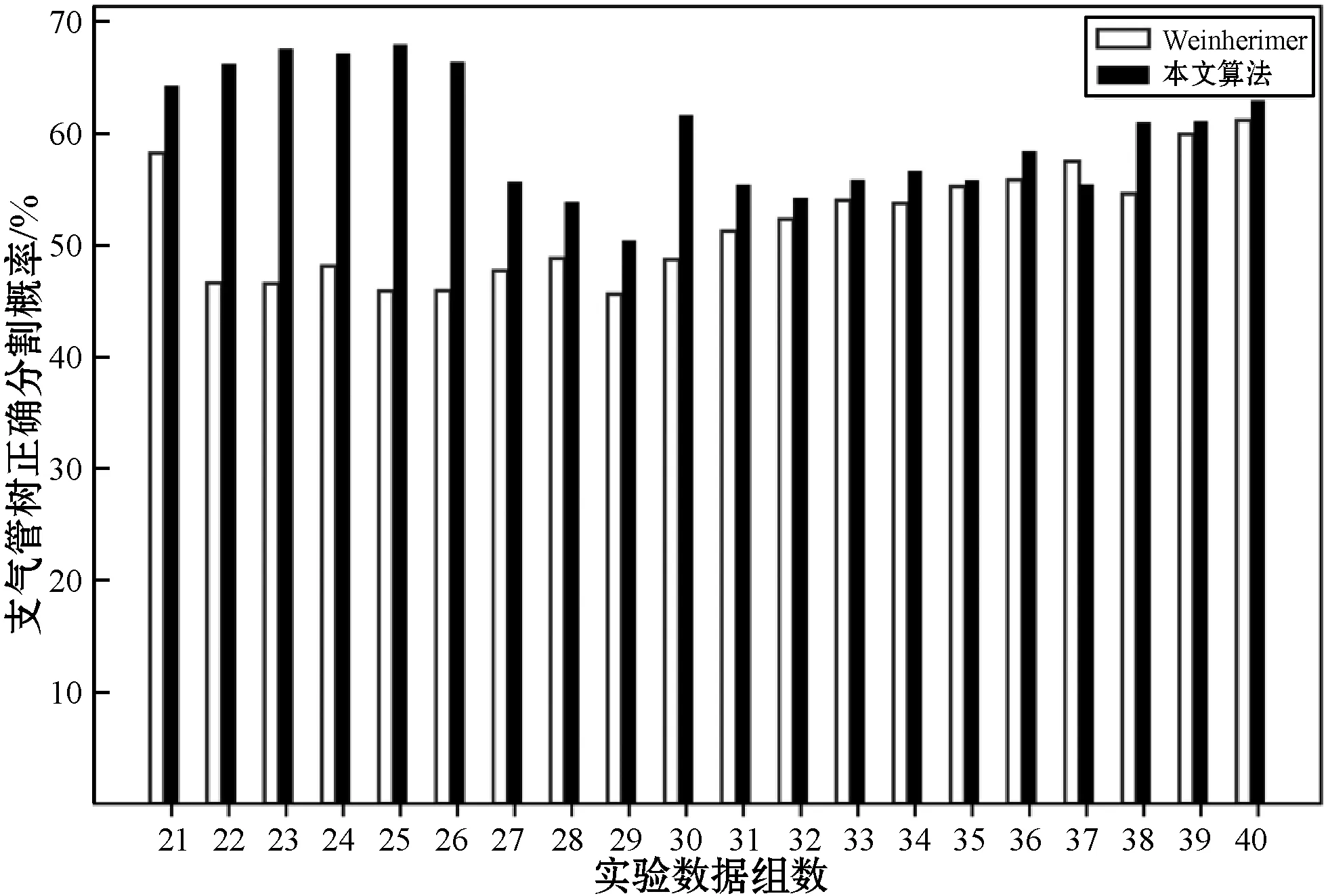
(a) 與Weinherimer等分割結果對比

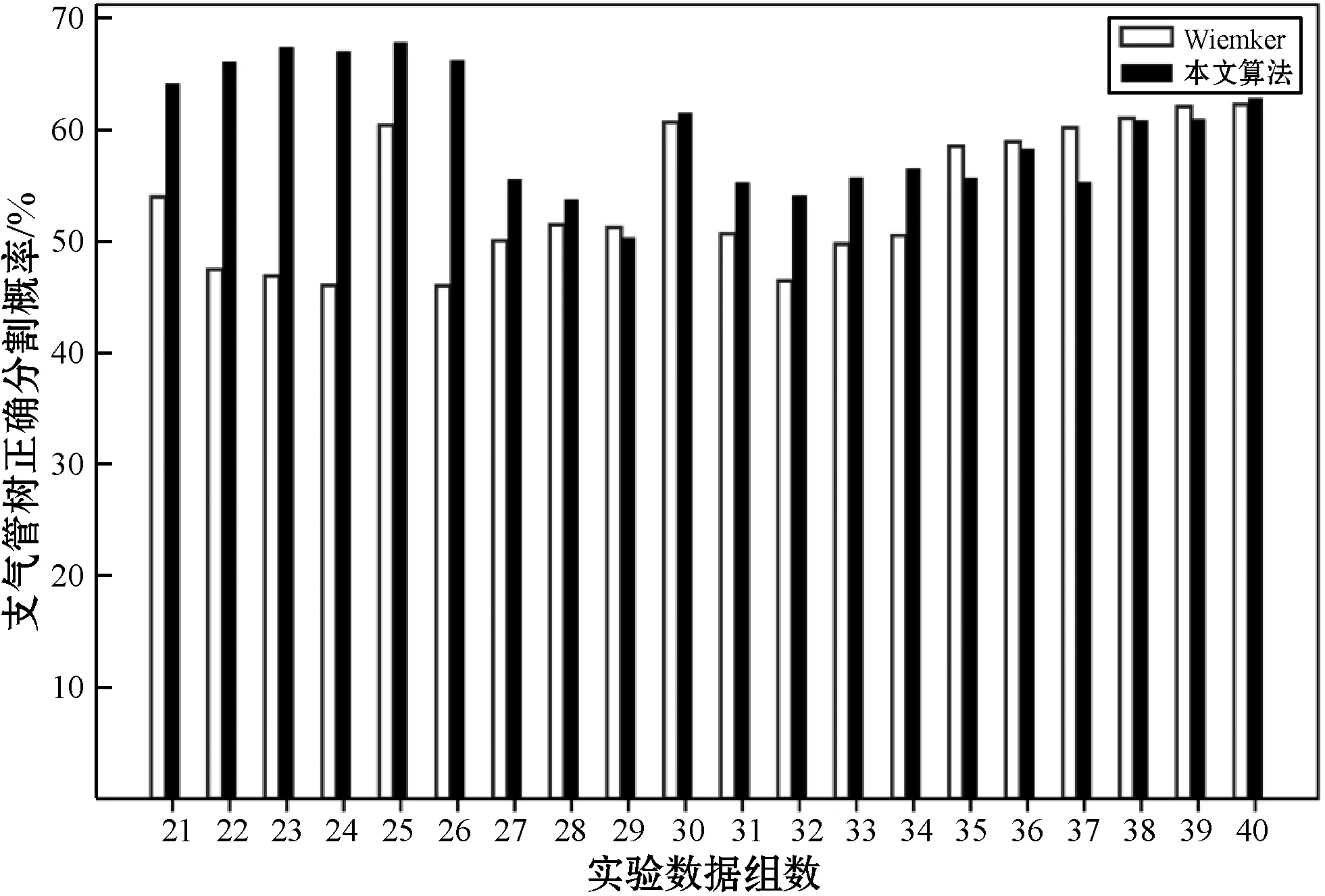
(b) 與Wiemker等分割結果對比圖6 正測到的分支數與總支氣管分支數比值對比圖

可以看出，本文算法分割的樹長，正確檢測到的支氣管樹基本上好于其他兩者，而且本文算法明顯具有更優秀的防泄漏性能。

3.3 與在EXACT09算法中的性能評測

圖7為本文算法與EXACT09競賽15種算法平均值的對比結果，其中:(a)為針對后20例測試數據所分割出正確分支的數目;(b)為針對后20例數據分割結果種泄露或錯誤的體積。本文算法在泄露極少的情況下達到了EXACT09競賽算法的平均水平線之上。

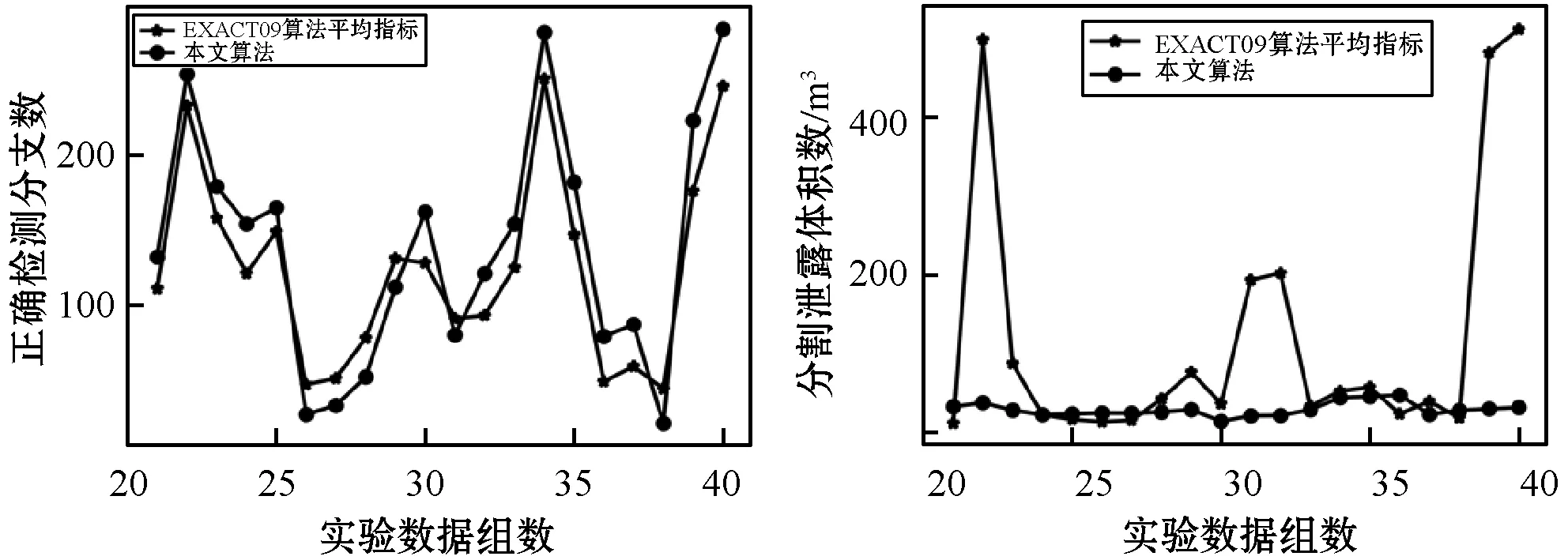
(a) (b)圖7 本文算法檢測到的分支數與15種EXACT09算法 平均檢測分支數對比圖

表1為本文算法與EXACT09的15個參賽算法評估結果，顯示了不同算法的樹長、假陽性概率以及檢測到的正確分支數的比例。

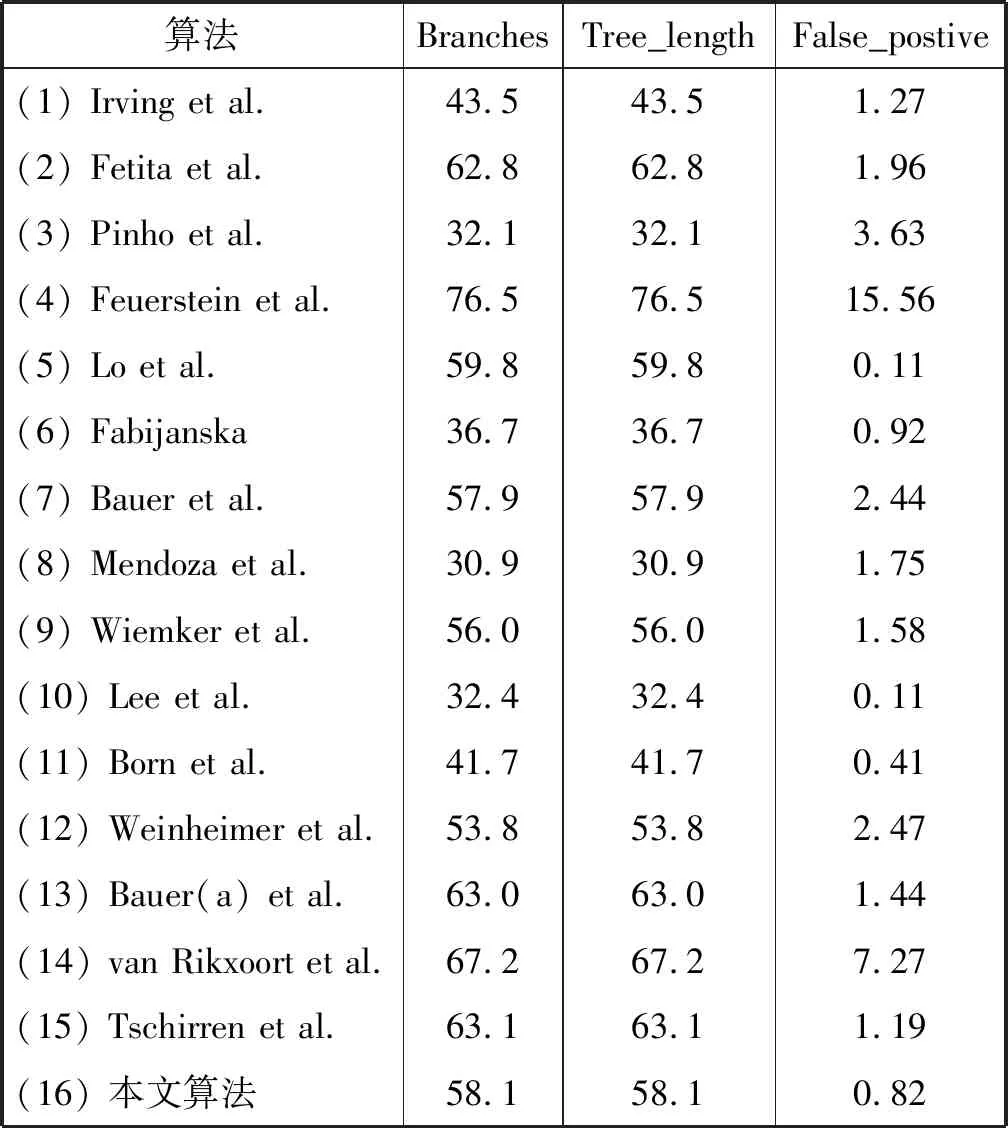
表1 使用20個測試用例的平均評估度量 %

圖8更直觀地顯示了不同算法的樹長、假陽性概率以及檢測到的正確分支概率，其中,(d)為檢測到的樹長與假陽性率的散點圖，顯示了不同算法的平均性能。可以看出，本文算法在假陽性極低的情況下可以獲得不錯的分割結果。

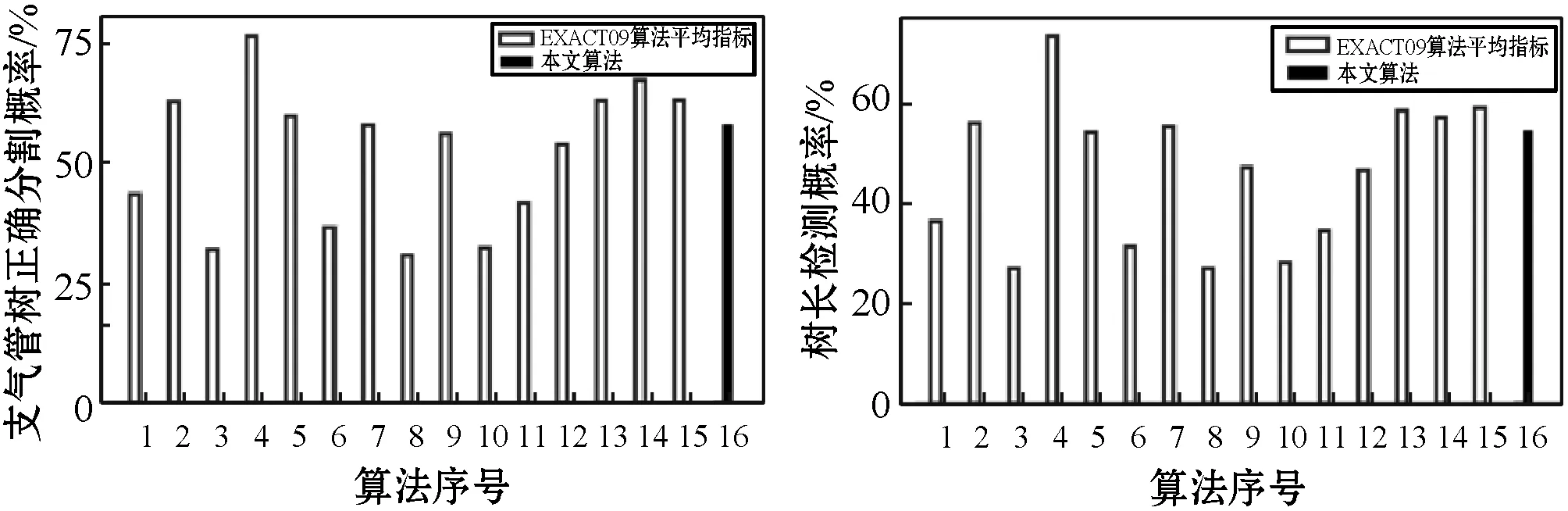
(a) (b)

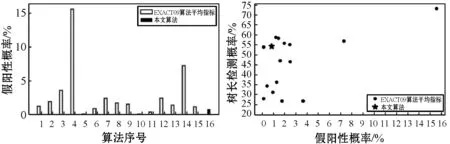
(c) (d)圖8 檢測到的樹長與假陽性率的散點圖

實驗結果表明，本文算法與其他三維方法相比，在不依賴于種子點的人工選擇，不需要訓練集的條件下能獲得更完整的肺氣管分割結果，且漏泄量更小。

4 結 語

本文提出了一種基于T-prim樹的肺氣管樹分割算法。首先結合區域生長算法與形態學灰度重建，初步分割出肺主支氣管。之后改進prim算法，結合一種基于馬爾可夫隨機場優化的分水嶺分割框架，使用T-prim最小生成樹算法構造出新的能量函數，利用構造出的T-prim樹結合這一優化分水嶺分割框架完成對細支氣管的分割。通過與EXACT09競賽算法的對比實驗驗證了本文算法在不需要手動操作、不需要訓練數據的情況下可以獲得優秀的分割效果，并且分割過程中的泄露量和錯誤率非常低。