基于運算符信息的數學表達式檢索方法

徐以聰,田學東,左麗娜

(河北大學 網絡空間安全與計算機學院,河北 保定 071002)

0 概述

在目前搜索引擎已經具備快速準確檢索文本的功能,同時關于文本相似度檢測的研究也較為成熟[1-3]的背景下,數學公式相似度的檢索問題被廣泛關注[4-6]。然而,數學表達式具有復雜的二維結構特征,傳統面向一維文本的檢索方法難以滿足其檢索需要。

關于數學表達式的檢索,國內外研究者取得了較多研究成果,但由于數學表達式的種類繁多且結構復雜,在其索引結構的建立與匹配方面仍有待研究。考慮到決定數學表達式含義的往往不是運算數,而是由運算符構成的表達式結構,本文設計一種基于運算符信息的數學表達式檢索方法,提取數學表達式中的運算符作為骨架并建立索引,在此基礎上尋找與目標表達式相似的數學表達式。

1 相關研究

目前,國內外學者已針對數學表達式檢索的問題提出了多種方法和模型。MCAT search system[7]采用基于路徑與基于哈希散列相結合的編碼方法對數學表達式進行編碼,從數學表達式、段落、文檔3個層面提取文本信息,并參與了NTCIR-12 MathIR任務[8]。文獻[9]設計的語義檢索系統支持盲人用戶進行數學學習,其先將數據庫中的數學表達式轉換為MathML編碼的表達式,再對MathML表達式中的公式進行語義分析,構造每個公式的樹狀子結構,通過該樹狀子結構以特征向量的形式提取特征。MathPD[10]通過定義表達式符號特征、特征描述符和粒度,運用粒度比較、特征比較、相似度度量的方法來判定2個文檔的相似度。VMEXT[11]是一款數學表達式可視化工具,其同時將表示元素和數學表達式的語義結構可視化,使用戶能夠快速發現MathML標記中不影響表達式表示的缺陷。文獻[12]針對數字數學圖書館設計和開發的Web用戶界面WebMIaS,允許用戶將文本自動生成的標準關鍵字與LaTeX或MathML格式的數學公式形式的關鍵字組合在一起,通過Web界面進行查詢操作。Min[13]是一個多模態的數學搜索界面,可以在臺式機以及平板電腦等設備的標準Web瀏覽器中運行,并通過外部Web服務實現數學符號的識別與解析功能。

文獻[14]提出一種基于2個索引的數學公式局部匹配檢索系統,其中一個索引將公式視為表達式樹,以每個節點到根節點的路徑構造反向索引,另一個索引是一個表,用于存儲表達式樹中每個節點的父節點和文本字符串。文獻[15]提出的數學表達式檢索和索引方法,索引中的每個鍵都是一對符號以及它們在表達式中的相對距離和垂直距離,可以解決部分匹配問題。文獻[16]設計的一種MathML格式的數學公式匹配算法,將數學公式表示為二叉樹,層次遍歷二叉樹得到結構碼,根據先序遍歷序列與中序遍歷序列是否相同判斷2個數學公式是否匹配。文獻[17]提出一種基于Ontology的數學表達式檢索方法,運用Ontology建立數學表達式及其概念之間的聯系并構建數學表達式語義本體庫,以達到輸入關鍵詞、概念、短語和數學名詞即可檢索數學表達式語義相關文獻的目的。

文獻[18-19]將數學表達式轉化為自底向上等價的樹結構用以解答數學應用題,首先構造具有不同結構和內部節點的候選樹,然后通過定義評分函數選擇最佳的候選樹。文獻[20]提出一種多方程數學表達式問題的求解方法,設計了語義表示語言DOL,用來表示自然語言文本的結構語義,其通過語義分析器將文本轉換為DOL樹,根據得分函數選擇得分最高的DOL樹。

文獻[21]提出一種基于協同過濾的數學表達式推薦方法,通過在數學表達式查詢輸入端加入數學表達式子式位置選擇模式,使檢索結果初步貼近用戶偏好。在此基礎上,采用模糊集方法以多特征指標對用戶偏好進行建模,并依據用戶行為的隸屬度函數構造用戶對數學表達式的評分矩陣。最后根據協同過濾算法的思想,通過設置閾值產生數學表達式的推薦列表,實現數學表達式的協同過濾推薦。

文獻[22]提出一種基于semi-operator樹生成子樹的層次泛化方法,該方法支持子結構匹配和模糊匹配,其在索引階段構建2個索引文件計算查詢公式與文檔的混合相似度得分,提高了在線查詢效率。文獻[23]在文獻[22]方法的基礎上設計改進的數學信息檢索系統,增加了表達式周圍的文本信息屬性,提高了查詢結果的合理性。

為使用戶可以方便地以數學公式作為查詢語言對科技文檔進行檢索,文獻[24]提出了一種基于數學表達式特征的科技文檔檢索模型。首先通過將公式解析為二叉樹得到數學表達式的子式信息,利用數學表達式及子式構造檢索特征向量;在索引階段,利用所提取的文檔特征向量構建分層結構的索引表;在匹配階段,對文檔向量采用tf-idf進行加權操作,利用余弦相似度對檢索向量和文檔向量進行相似度計算,從而得到一個有序的文檔檢索結果。

文獻[25]提出一個能夠在維基百科中檢索數學公式的工具WikiMirs,基于文本和空間相似性搜索相似的數學公式。該文提出一種從數學公式表示樹生成子樹的層次泛化方法,并根據這些樹在不同層次上的匹配程度計算相似度。

文獻[26]提出MIaS,設計了一個基于MathML表示樹的索引結構來檢索數學表達式,其利用tf-idf權重法對表達式進行排序。文獻[27]則針對線性代數表達式,設計了一種線性代數表達式的索引與匹配方法,根據線性代數表達式的種類對其進行分類,并定義相應的擴充運算,據此構建索引文件,設計線性代數表達式匹配算法,實現靈活的檢索模式,提高檢索結果的相關性。

2 數學表達式骨架提取

公式描述結構[28-30](Formula Description Structure,FDS)用于對數學表達式的描述,更便于建立數學表達式索引和實現數學檢索。因此,本文利用改進的FDS解析算法對LaTeX格式數學表達式進行分析,并提取數學表達式的結構信息。

2.1 FDS提取算法

數學表達式每個節點上的信息存儲在FDS向量(Symbol,Level,Operator,Flag)中,其中:Symbol為表達式的當前符號;Level表示當前符號所在的層次信息,主基線層次為0,其余層次在上一層次的基礎上加1;Operator表示當前符號是否為運算符,如果是運算符,值為1,否則為0;Flag表示當前符號的空間位置,對應over、superscript、subscript、under、inclusion、upper left(ul) 和lower left(ll)7種情況,Fcode為Flag的值,分別對應1、2、3、4、5、6、7。部分表達式符號空間位置關系如表1所示。

表1 部分表達式符號空間位置關系

例如,LaTeX公式“[x=frac{{-bpmsqrt{{b^2} -4ac}}} {{2a}} ]” 對應的原型公式為:

(1)

其FDS解析數據見表2。當Fcode為0時,表示該節點位于主基線層。

表2 式(1)的FDS信息

由于本文設計的索引結構不需要存儲表達式的所有節點信息,因此有必要對原有的FDS算法進行修改,如算法1所示。

算法1FDS解析算法

輸入LaTeX數學表達式

輸出數學表達式的FDS信息

步驟1將隱式運算符關鍵字添加到現有運算符字典中。

步驟2遞歸遍歷LaTeX表達式,查找運算符字典,確定每個關鍵字節點長度,并為每個節點分配Level編號。

步驟3依次分析每個關鍵字節點,并記錄該節點的Level、Operator和Fcode信息。

步驟4如果Operator為1,則保留該節點,否則舍棄。保留的節點構成了表達式的FDS信息表。

上述算法的主要過程是線性掃描LaTeX格式的數學表達式,以一層循環為主,循環體內包含選擇語句對每個關鍵字進行判斷,若為運算數則返回循環條件對下一個關鍵字進行判斷;若為運算符則提取其信息。對一個長度為n的LaTeX表達式,共需執行n次元操作,算法的時間復雜度為O(n)。

除了存儲關鍵字本身,字典還存儲關鍵字的類型,這些類型之間用“#”分隔。根據關鍵字的類型,可以判斷當前關鍵字是否為運算符,然后由運算符判斷當前關鍵字的層次信息。算法修改后獲取的式(1)的FDS信息如表3所示。可以看出,原有信息表中Operator字段值為1的節點全部保留,為0的全部舍棄。此外,將隱含的指數符號“^”視為運算符添加進來,層次與標志位均與其指數位相同。“^”作為一種隱含符號,與層次的變化有關,其他像“ab”中的乘法將不包括在內,因為它不會導致左右2個節點的層次變化。

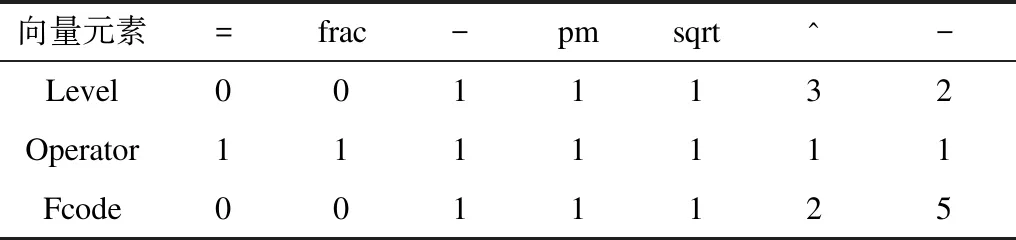
表3 算法修改后式(1)的FDS信息

2.2 公式骨架提取

數學表達式的結構由運算符組成,運算符決定了數學表達式的基本運算含義。考慮以下2個公式:

a2+b2=c2

(2)

x2+y2=z2

(3)

雖然構成上述2個表達式的運算數不同,但結構與含義實際上是完全相同的,其一般形式如下:

i*+j*=k*

(4)

其中,“*”表示指數,不限于等于2。為便于觀察,將式(2)和式(3)以二叉樹的形式描述并提取它們的骨架,分別如圖1～圖3所示。顯然,式(2)和式(3)除了構成表達式的運算數不同以外,運算符及其所在層次是相同的,2個表達式具有完全相同的結構。因此,式(2)和式(3)互為相似表達式。

圖1 式(2)的二叉樹

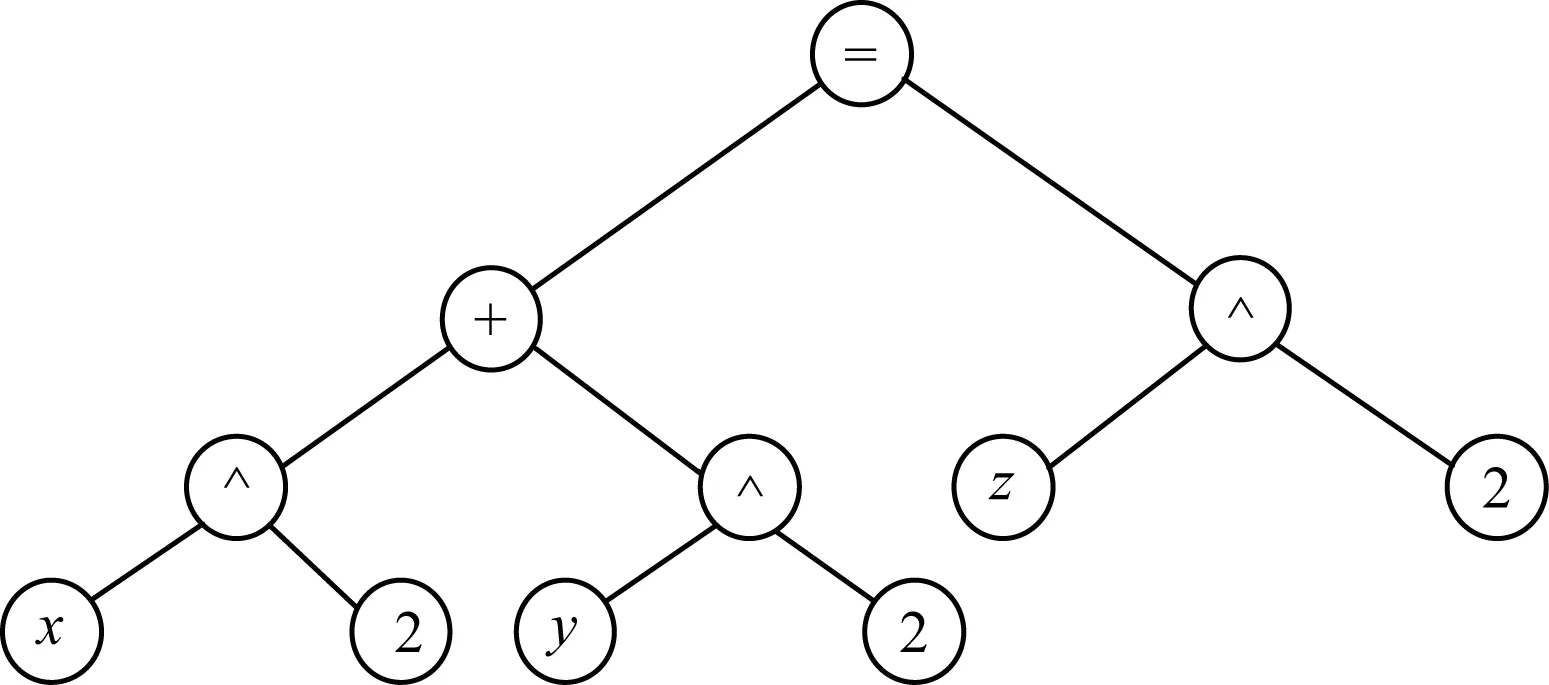
圖2 式(3)的二叉樹

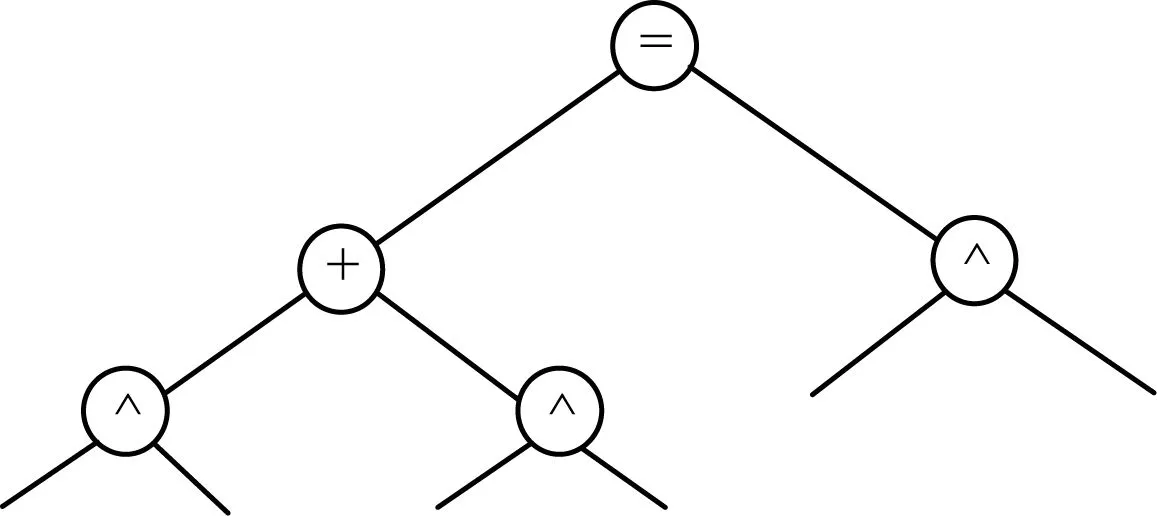
圖3 式(2)和式(3)的骨架樹

本文的研究目標是檢索出具有完全相同或是部分相同結構的相似表達式,其中部分相同是指2個表達式的結構至少具有一個在同一層次相同的運算符。

3 數學表達式索引結構設計與匹配

3.1 運算符與骨架存儲結構設計

在對數學表達式的結構(以下簡稱為骨架)建立索引之前,首先對單個運算符進行結構化設計,除了考慮構成骨架的運算符本身以外,還需要考慮運算符在表達式中的層次。

定義1每個運算符與其層次組成一個S-L對(S:Symbol,L:Level),其中,Symbol表示當前運算符本身的符號,Level表示當前運算符的層次。單個運算符的存儲結構如圖4所示。

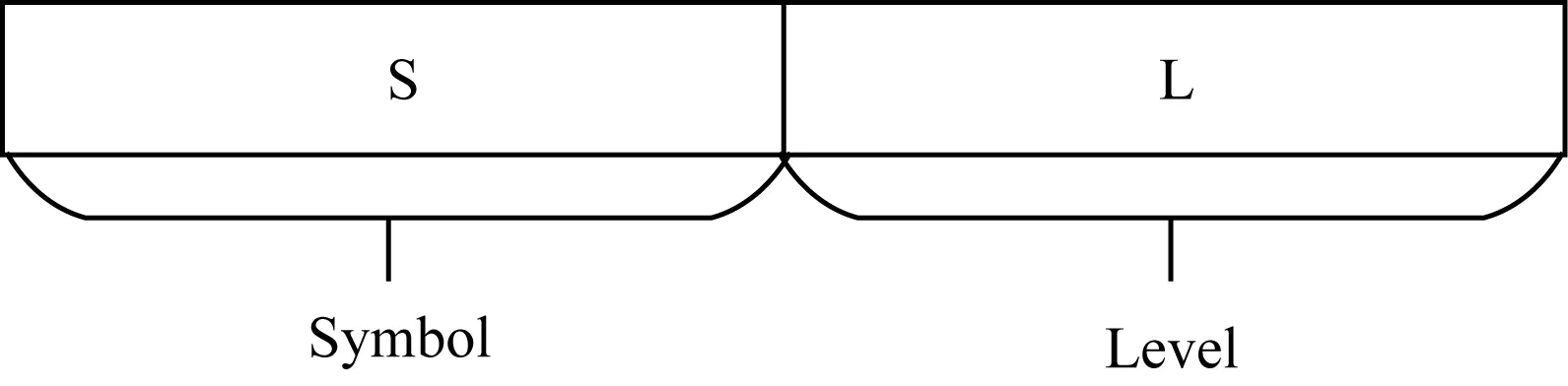
圖4 單個運算符的存儲結構

對于一個完整的表達式,假設共有N個操作符,將表達式所有的單個操作符存儲結構連接起來即可得到表達式的完整骨架存儲結構,如圖5所示。由于N的取值不同,因此不同表達式的完整骨架結構是不等長的。

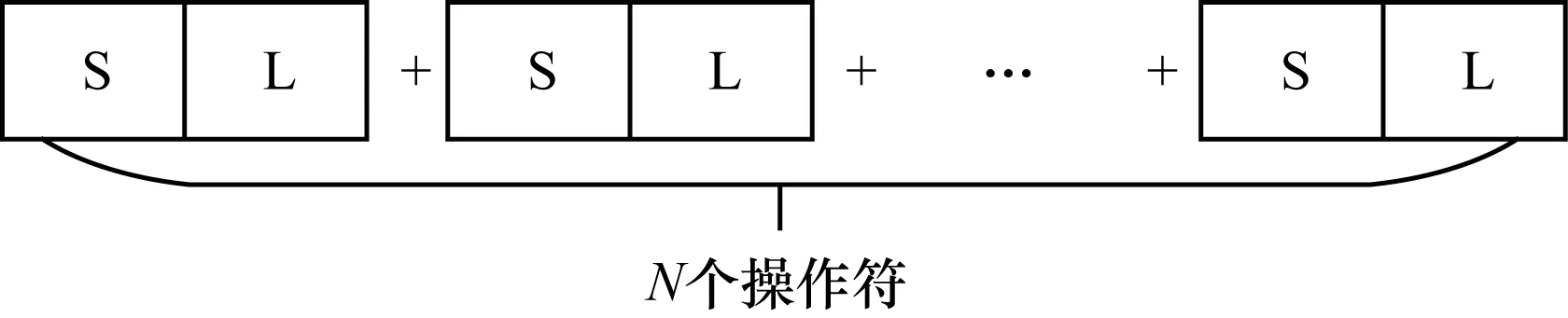
圖5 完整骨架存儲結構

3.2 數學表達式索引結構

定義2一個完整的數學表達式具有如下形式的索引結構:expIndex:{expId,fileId,expCode,expInfo},其中,expId為表達式的序號,fileId為當前表達式所在文檔的編號,expCode為表達式的骨架結構編碼,expInfo為LaTeX形式的表達式本身。

定義3含有表達式的文檔索引結構形式為fileIndex:{fileId,fileName},其中,fileId為文檔的編號,fileName為當前文檔的名稱。在檢索時,首先提取待檢索表達式的expCode,然后在數據庫中檢索是否有相同或相似的expCode與之匹配,若匹配結果不為空,即可根據檢索結果表達式中的fileId找到對應的fileName。

3.3 數學表達式匹配算法

定義4設O為任意表達式F的所有S-L對的集合,sl1,sl2,…,sln為O的元素,記為O={sl1,sl2,…,sln},其中,sli(1≤i≤n)分別為F的第i個S-L對,n為S-L對的個數。

設S為數據集中全部表達式S-L對的集合,O1,O2,…,Om為S的元素,S={O1,O2,…,Om},其中,m為表達式的個數,S的子集記為Si(1≤i≤n)。

算法的執行步驟數與目標表達式的長度成正比,表達式的長度越長,骨架結構就越長,從而n也就越大,執行的步驟也越多。如圖6所示,可見式(1)的骨架結構為(=/0)+(frac/0)+(-/1)+(pm/1)+(sqrt/1)+(^/3)+(-/2)。

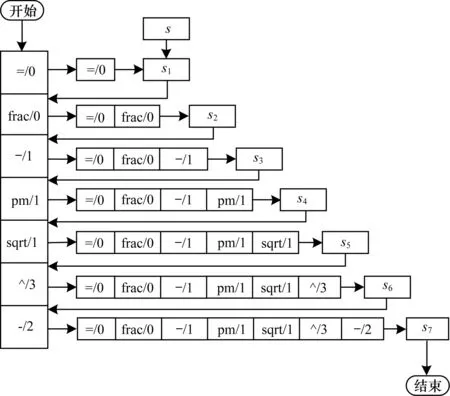
圖6 式(1)檢索過程

數學表達式匹配算法描述如下:

算法2數學表達式匹配算法

輸入LaTeX數學表達式

輸出與目標表達式相似的表達式集合

步驟1輸入待檢索的目標表達式F,利用算法1獲得F的所有S-L對的集合O。

步驟2從O中提取sl1,并在S中檢索出所有包含sl1的表達式,構成集合S1。

步驟3從O中提取sl2,并在S1中檢索出所有包含sl2的表達式,構成集合S2。

……

步驟n+1從O中提取sln,并在Sn-1中檢索出所有包含sln的表達式,構成集合Sn,即與目標表達式相似的表達式集合。

算法步驟1的時間復雜度為O(n),步驟2是第1次從S中提取運算符,因此,復雜度為O(m),從步驟2到步驟n+1,因為集合Si逐漸變小,所以每步的復雜度均小于O(m),又因為n遠小于m,所以算法的總時間復雜度小于O(n)+nO(m),即小于nO(m)。

4 實驗結果與分析

4.1 實驗數據與環境

本文實驗從ntcir_12_mathir_wikipedia_corpus數據集中獲得31 742個文檔,其中包含519 588個數學表達式。編程語言為C#,采用C/S模式,實驗環境為Intel(R) Core(TM) i7-7700 CPU,3.6 GHz,內存為8 GB。操作系統是Microsoft Windows [version 10.0.17134.407]。

4.2 索引大小與查詢響應時間

表4、表5分別列出了本文實驗索引文件以及文獻[25]索引文件的大小,圖7顯示了隨著公式數量的增加索引文件大小的變化情況。

表4 本文實驗索引數據

表5 文獻[25]索引數據

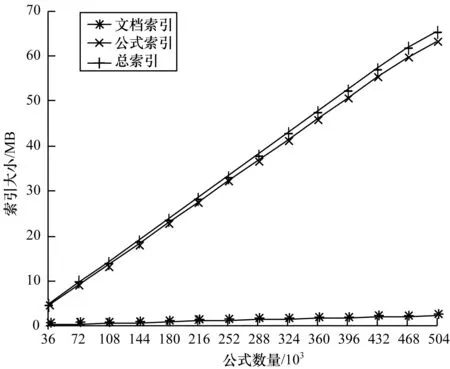
圖7 索引大小與公式個數的關系

隨著文檔和公式數量的增加,文檔和公式索引的大小逐漸增大,但增速較低。本文方法只對運算符建立索引,放棄了運算數,大幅減小了索引文件的大小,節省了存儲空間。與表5所示的文獻[25]索引相比,本文索引較為節省空間。同時由圖7可知,最初公式索引和總索引2條曲線幾乎重合。文檔索引曲線一直在水平軸附近,與其他2條曲線不同,變化緩慢,公式個數則與3個索引曲線之間存在線性函數關系。

對不同結構的表達式進行檢索實驗,結果如表6所示,其中平均檢索時間是指10次檢索時間的平均值,均在可接受范圍內。

表6 部分表達式檢索情況

由表6可以看出:目標表達式結構越簡單,骨架結構越簡單,結果表達式越多,時間開銷越低;目標表達式的結構越復雜,結果表達式就越少,所需的時間也就越長。

4.3 個例研究

對式(1)的部分檢索結果如表7所示。由于查詢結果數量較多,表中只列出前15個查詢結果(本文排序方法的第一步是找到最接近目標公式長度的公式。如果有2個長度相同的結果公式,則ID較小的排在前面)。可以看出,除了能夠檢索出與目標表達式完全相同的表達式外,本文方法還可以檢索出具有相同結構但運算數不同的表達式,例如第68 421個和第248 575個表達式,這樣即可消除一般運算數的影響。

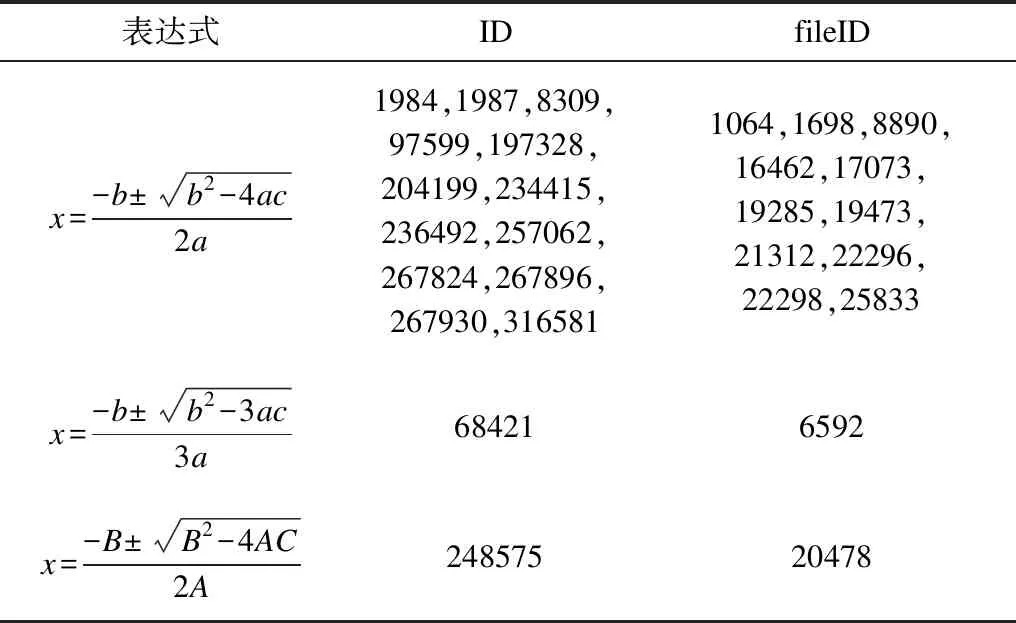
表7 式(1)部分檢索結果

4.4 對比實驗

表8給出了WikiMirs 和本文系統檢索結果的前5個查詢結果。

表8 2種方法的Top-5查詢結果

5 結束語

本文通過引入公式描述結構,提出一種基于運算符信息的數學檢索方法,其由FDS分析、索引和匹配3個主要步驟組成。將數學表達式輸入到FDS程序中獲得運算符信息,在此基礎上建立數學表達式索引,并通過匹配算法找出與目標表達式相似的數學表達式。實驗結果表明,該方法能夠檢索相似的表達式,具有較高的檢索效率,并且不受一般運算數的影響。由于本文方法主要面向表達式,未考慮表達式在文檔中的重要性,因此下一步將在表達式和文檔之間添加關系屬性,以檢索出滿足用戶需求的文檔。此外,還將優化其索引結構,加快檢索速度。