二階多智能體系統(tǒng)參數(shù)自適應(yīng)的有限時間一致性算法
崔 艷,李慶華
(山西師范大學(xué) 物理與信息工程學(xué)院,山西 臨汾 041000)
0 概述
近年來,多智能體系統(tǒng)的分布式協(xié)同控制逐漸成為控制領(lǐng)域的研究熱點,其在實際生活中有很多應(yīng)用,如多機(jī)器人編隊控制[1]、無人機(jī)編隊飛行控制[2]和水下自動駕駛車[3]等。一致性是多智能體系統(tǒng)分布式協(xié)同控制的基本問題[4-6]。在衛(wèi)星群的同步運行、多飛行器飛行、多自主機(jī)器人探測器等實際問題中,系統(tǒng)需要在有限時間內(nèi)實現(xiàn)一致收斂,因此,研究在有限時間內(nèi)系統(tǒng)的快速收斂具有重要意義[7-8]。
在一致性問題研究中,收斂速度是一個重要的性能指標(biāo)。文獻(xiàn)[9]指出代數(shù)連通性決定了多智能體系統(tǒng)的一致收斂速度,文獻(xiàn)[10]通過增大代數(shù)連通性提高系統(tǒng)的收斂速度,上述研究說明,代數(shù)連通性提高可以加快收斂速度。文獻(xiàn)[11]考慮最優(yōu)頂點配置,使生成圖的代數(shù)連通性達(dá)到最大,并將任意2個智能體間的權(quán)重作為距離構(gòu)造函數(shù)。文獻(xiàn)[12]將半正凸函數(shù)的解作為鄰接矩陣元素,提高系統(tǒng)的收斂速度。然而,上述工作都是基于合適的拓?fù)浣Y(jié)構(gòu)進(jìn)行分析,并沒有討論如何利用智能體間的控制協(xié)議來提高收斂速度,因此不具備自適應(yīng)的特點。此外,與漸近一致相比,有限時間一致具有響應(yīng)快、準(zhǔn)確性高和魯棒性好等優(yōu)點,鑒于此,文獻(xiàn)[13]對一階多智能體系統(tǒng)中的有限時間一致性問題進(jìn)行研究。文獻(xiàn)[14]將非線性系統(tǒng)參數(shù)化,僅利用每個智能體與其相鄰智能體之間的局部相對位置狀態(tài)信息,提出分散有限時間自適應(yīng)一致性算法,使系統(tǒng)達(dá)到一致。文獻(xiàn)[15]通過選擇適當(dāng)?shù)淖钚【仃嚩囗検?在離散時間系統(tǒng)中給出一致性算法。文獻(xiàn)[16]將智能體之間位置與速度的差值作為反饋系數(shù)函數(shù),提出控制協(xié)議,但系統(tǒng)的收斂速度較慢且反饋系數(shù)為固定值。文獻(xiàn)[17]分析了自適應(yīng)反饋系數(shù)在一致性算法中的作用,但并沒有明確提出確定系數(shù)的方法。
本文針對二階多智能體系統(tǒng)提出一種反饋系數(shù)自適應(yīng)的有限時間一致算法。該算法利用相鄰智能體之間的位置差值和速度差值作為反饋系數(shù)來預(yù)測飛行器多智能體下一時刻的狀態(tài)。
1 預(yù)備知識
有向圖G=(v,ε,A)表示多智能體系統(tǒng)的通信結(jié)構(gòu)。其中,v={v1,v2,…,vn}稱為G的節(jié)點集,ε∈v×v稱為邊緣集,A=[aij]是G的鄰接矩陣。在圖G中,從節(jié)點vi到節(jié)點vj的有向邊表示為eij=(vi,vj)∈ε。邊的鄰接元素為正,即eij∈ε?aij>0且有aij=0,無向圖的鄰接矩陣具有對稱性。
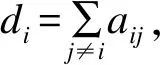
2 實際系統(tǒng)模型與協(xié)議設(shè)計
具有n個飛行器的二階動態(tài)系統(tǒng)如下:
(1)
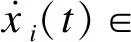
定義1對于式(1)所示的多智能體系統(tǒng),如果存在一個停息時間T0∈[0,+∞),則滿足式(2)時,二階系統(tǒng)達(dá)到有限時間一致[16]。
?i,j=1,2,…,n
(2)
本文研究有限時間內(nèi)的二階多智能體系統(tǒng)一致性,并提出以下控制協(xié)議:
(3)
為預(yù)測下一時刻飛行器的狀態(tài)并加快收斂速度,利用飛行器間的位置差值與速度差值,設(shè)計協(xié)議ui(t)中的參數(shù)bij和cij的計算公式,具體如下:
(4)
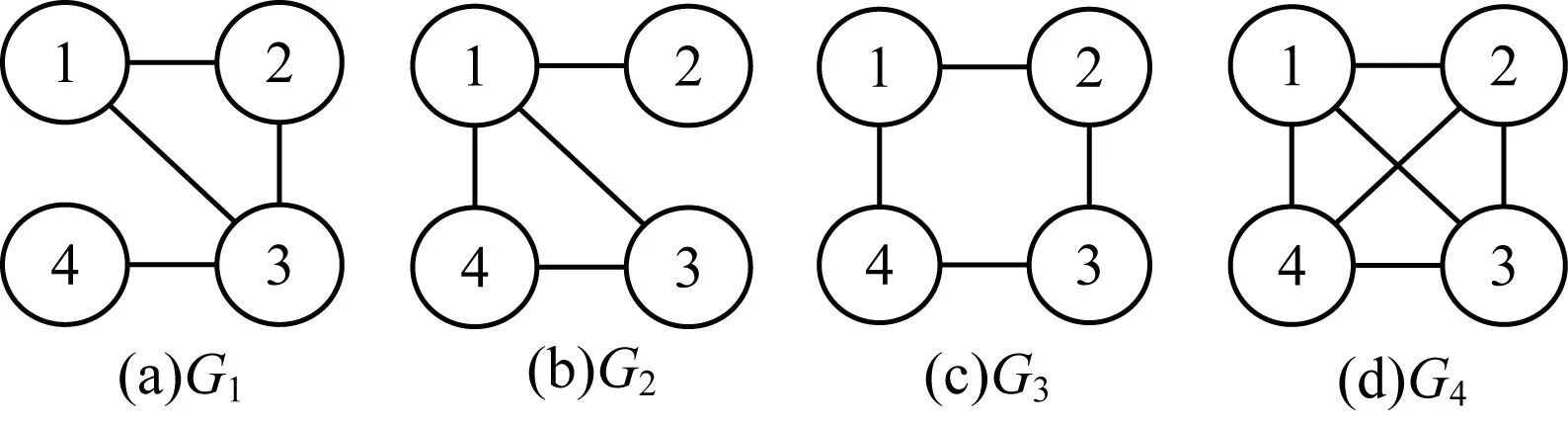
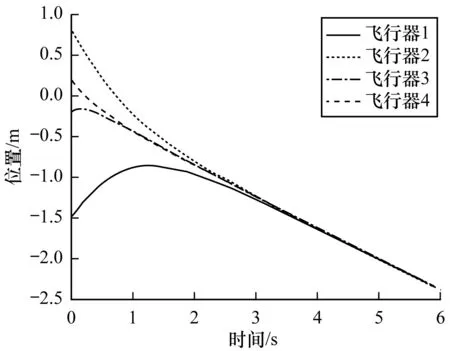
其中,|xj-xi|和|vj-vi|分別表示2個飛行器之間的位置差值與速度差值,0 定義2非線性系統(tǒng)的定義如下: (5) 連續(xù)向量流f(x)=[f1(x1),f2(x2),…,fn(xn)]T,與帶有擴(kuò)張的(r1,r2,…,rn)ri>0的度是齊次的,對于任意的ε>0,有如下公式: fi(εr1x1,εr2x2,…,εrnxn)=εκ+rifi(x),i=1,2,…,n (6) 定義3式(5)所示的系統(tǒng)是齊次的,如果其向量流也是齊次的,并且滿足如下公式: (7) (8) 定理1對于n個飛行器構(gòu)成的多智能體系統(tǒng)(即式(1)),G是無向連通的,存在協(xié)議參數(shù)bij和cij為正時,式(3)協(xié)議可以使系統(tǒng)達(dá)到有限時間一致。 證明誤差定義如下: (9) (10) 記mij=2-βij,nij=2-λij,則有如下公式: (11) 由式(1)、式(4)和式(9)可知: (12) 取Lyapunov函數(shù)V=V1+V2+V3,其中: (13) 對Lyapunov函數(shù)求導(dǎo),得到以下公式: (14) (15) (16) (17) 下面證明系統(tǒng)可在有限時間內(nèi)達(dá)到一致。令: ψn(t),ψn+1(t),ψn+2(t),…,ψ2n(t)]T 則式(12)可以改寫為如下形式: fi(εr1ψ1,εr2ψ2,…,εrnψn,εrn+1ψn+1,…,εr2nψ2n)= εrn+iψn+i=εR2fi(ψ)=εR1+κfi(ψ)=εri+κfi(ψ), i=1,2,…,n 且有: fn+i(εr1ψ1,εr2ψ2,…,εrnψn,εrn+1ψn+1,…,εr2nψ2n)= εR2+κfn+i(ψ)=εrn+i+κfn+i(ψ), i=1,2,…,n,j=1,2,…,n 由上述分析可知,ψi→0,ψn+i→0,故γ>0,存在t0>0,說明ψi(t)與ψn+i(t)是有界的,具體過程如下: 綜上所述,由引理2可知,式(3)控制協(xié)議可在有限時間內(nèi)實現(xiàn)一致性收斂。 注釋1文獻(xiàn)[16]中提出的一致性協(xié)議如下: (18) 當(dāng)系統(tǒng)未達(dá)到收斂狀態(tài)時,存在以下情形: (19) 由注釋1可知,這是一種實際可操作的參數(shù)確定方法,而本文的參數(shù)設(shè)計方式可實現(xiàn)對不同二階飛行器智能體輸入狀態(tài)的自適應(yīng)調(diào)節(jié)。 注釋2由于本文Lyapunov函數(shù)求導(dǎo)后小于文獻(xiàn)[16]中Lyapunov函數(shù)求導(dǎo)的結(jié)果,因此本文一致性控制算法的收斂速度更快。 由于外界擾動等因素的影響,無法保證網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)始終保持不變,因此考慮切換拓?fù)淝樾尉哂兄匾饬x。 (20) 引理3考慮以下非線性系統(tǒng): (21) 證明取Lyapunov函數(shù)V=V1+V2+V3,其中: 由于切換拓?fù)渲猩婕暗拿總€拓?fù)涫沁B接且未改變的(證明過程與定理1類似),由引理3可知,系統(tǒng)是有限時間穩(wěn)定的。實例說明過程類似于固定拓?fù)涞姆治觥?/p> 飛行器的發(fā)展給人們的日常生活帶來了極大的便利,越來越多的人愿意接受并使用這些新產(chǎn)品。飛行器在植保、快遞、搜救、航拍以及巡檢方面的普及速度非常快,而其一致性追蹤在實際生活中更是應(yīng)用廣泛。一致性追蹤需要多個飛行器協(xié)同合作,可以在有限時間內(nèi)更快速高效地完成高強(qiáng)度工作,方便人們的日常生活。未來,飛行器將越來越多地取代傳統(tǒng)的作業(yè)方式,其發(fā)展前景也非常令人期待。 針對多智能體系統(tǒng)的研究主要包括多智能體的一致性、編隊控制、聚集等方面的問題。多智能體系統(tǒng)通過控制相鄰飛行器之間的位置與速度,在有限時間內(nèi)實現(xiàn)一致性追蹤,并預(yù)測下一時刻飛行器的狀態(tài)。 本節(jié)通過實例給出具體分析。以包含4個飛行器的多智能體系統(tǒng)為例,各飛行器之間的通信拓?fù)浣Y(jié)構(gòu)如圖1所示。其中,拓?fù)浣Y(jié)構(gòu)的所有非零連接權(quán)值均為1,假設(shè)4個飛行器位置的初始狀態(tài)為x(0)=[-1.5,0.8,-0.2,0.2]T,速度的初始狀態(tài)為v(0)=[0.9,-1.2,0.4,-1]T。 圖1 多智能體系統(tǒng)的拓?fù)浣Y(jié)構(gòu)Fig.1 Topological structure of a multi-agent system 選取圖1(d)作為固定拓?fù)浣Y(jié)構(gòu),利用相鄰飛行器之間位置與速度的差值作為一致性反饋系數(shù)bij和cij,并提出式(3)所示的一致性協(xié)議,同時定義位置與速度之間的誤差進(jìn)行仿真。圖2和圖3分別給出所有智能體的位置和速度狀態(tài)信息,可以看出,最終4個飛行器的位置與速度都趨于一致,共同完成工作。圖4和圖5分別給出每個飛行器的位置和速度與平均值之間的誤差,可以看出,最終位置誤差趨于一致。綜上所述,4個飛行器能夠在有限時間內(nèi)達(dá)到一致跟蹤,且達(dá)到一致所用的時間較短,因此,其協(xié)同工作完成任務(wù)的效率較高。 圖2 固定拓?fù)浣Y(jié)構(gòu)位置仿真曲線Fig.2 Simulation curve of position in a fixed topologicalstructure 圖3 固定拓?fù)浣Y(jié)構(gòu)速度仿真曲線Fig.3 Simulation curve of speed in a fixed topologicalstructure 圖4 固定拓?fù)浣Y(jié)構(gòu)位置誤差仿真曲線Fig.4 Simulation curve of position difference in a fixedtopological structure 圖5 固定拓?fù)浣Y(jié)構(gòu)速度誤差仿真曲線Fig.5 Simulation curve of speed difference in a fixedtopological structure 考慮切換拓?fù)涞那樾?4個飛行器之間的通信信息關(guān)系如圖1所示,其切換順序為(a)→(b)→(c)→(d)→(a)。在各飛行器之間進(jìn)行信息交換,應(yīng)用本文在切換拓?fù)湎碌囊恢滦詤f(xié)議,即式(20)進(jìn)行仿真,可得到切換拓?fù)淝樾蜗?個飛行器位置與速度的狀態(tài),如圖6和圖7所示。可以看出,最終飛行器的位置與速度能在有限時間內(nèi)實現(xiàn)一致跟蹤。圖8和圖9分別為每個飛行器的位置和速度與平均值之間的誤差,可以看出,最終誤差趨于一致。綜合以上分析可得,在切換拓?fù)淝樾蜗?即4個飛行器之間的信息交流的軌跡發(fā)生變化時,多智能體系統(tǒng)能夠在有限時間內(nèi)達(dá)到一致跟蹤,且達(dá)到一致的速度較快。切換拓?fù)淝樾慰紤]了復(fù)雜網(wǎng)絡(luò)之間的信息交換,且其方式更加靈活,因此,切換拓?fù)涞那樾卧趯嶋H應(yīng)用中更為普遍和重要。 圖6 切換拓?fù)浣Y(jié)構(gòu)位置仿真曲線Fig.6 Simulation curve of position in a switching topologicalstructure 圖7 切換拓?fù)浣Y(jié)構(gòu)速度仿真曲線Fig.7 Simulation curve of speed in a switching topologicalstructure 圖8 切換拓?fù)浣Y(jié)構(gòu)位置誤差仿真曲線Fig.8 Simulation curve of position difference in a switchingtopological structure 圖9 切換拓?fù)浣Y(jié)構(gòu)速度誤差仿真曲線Fig.9 Simulation curve of speed difference in a switchingtopological structure 本文提出一種二階多智能體系統(tǒng)參數(shù)自適應(yīng)的有限時間一致性算法。利用位置和速度的差值作為反饋系數(shù),實現(xiàn)二階系統(tǒng)參數(shù)的自適應(yīng)一致,通過構(gòu)造Lyapunov函數(shù)并利用齊次理論,分析系統(tǒng)在有限時間內(nèi)達(dá)到穩(wěn)定的條件。仿真結(jié)果表明,該算法能夠使多智能體系統(tǒng)在有限時間內(nèi)實現(xiàn)一致跟蹤,且收斂速度較快。下一步將針對具有干擾和不確定性的高階多智能體系統(tǒng)進(jìn)行一致性問題研究。3 相關(guān)定義和引理
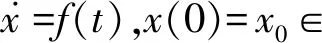
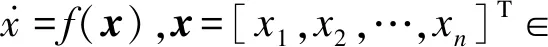
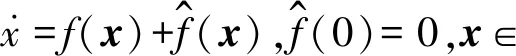
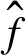

3.1 固定拓?fù)淝樾?/h3>
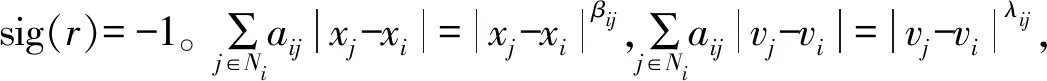
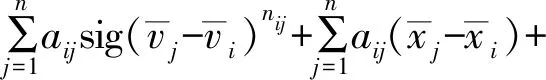
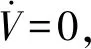
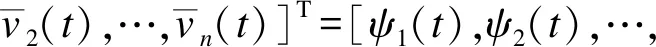
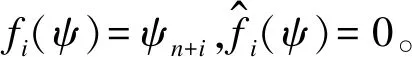
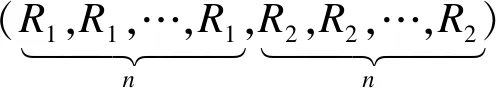
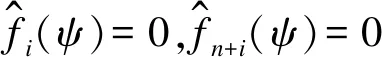
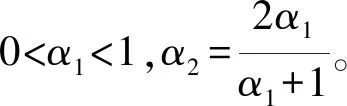
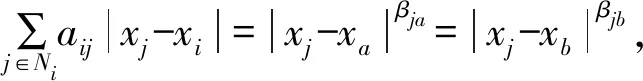
3.2 切換拓?fù)淝樾?/h3>
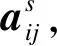
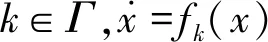
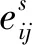
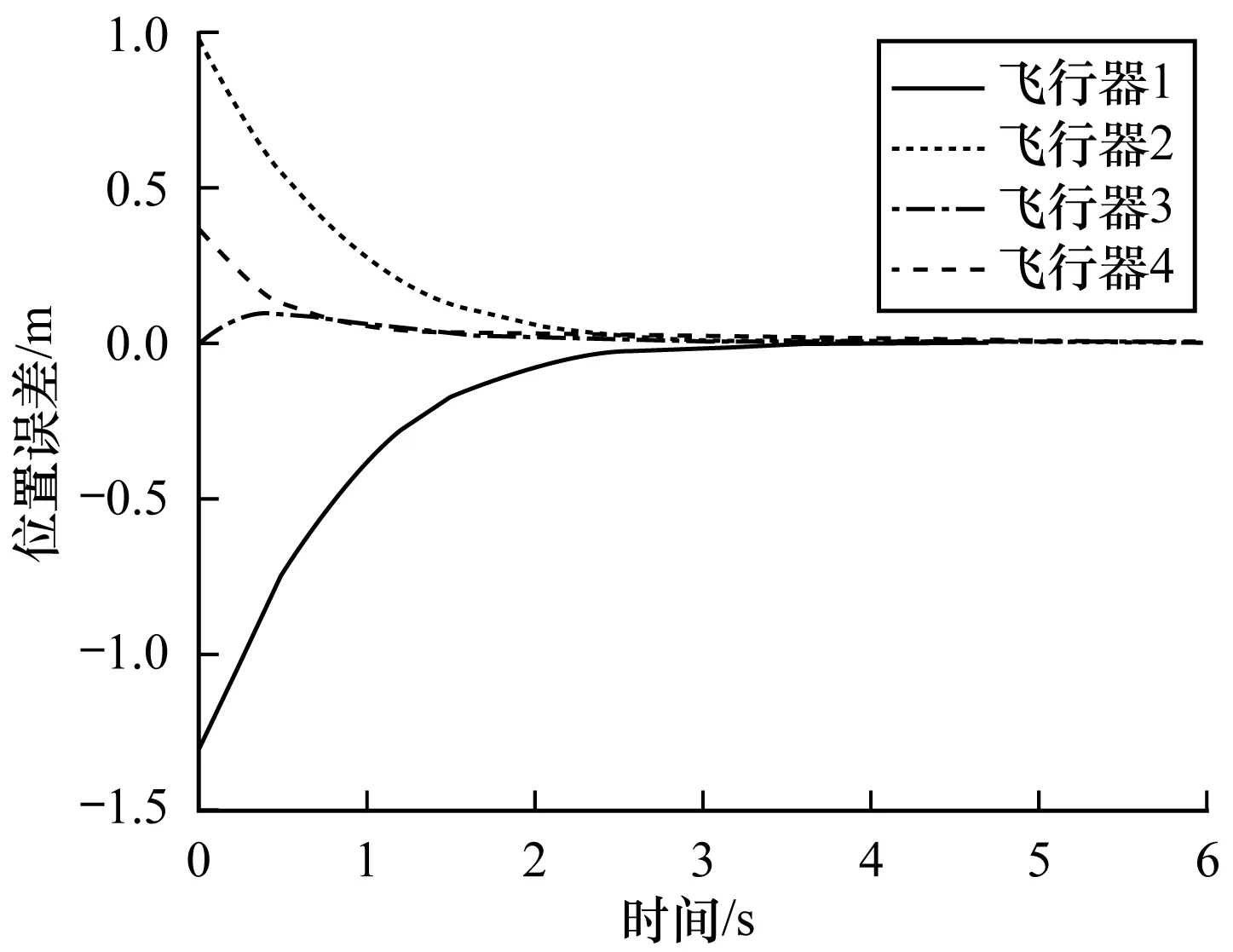
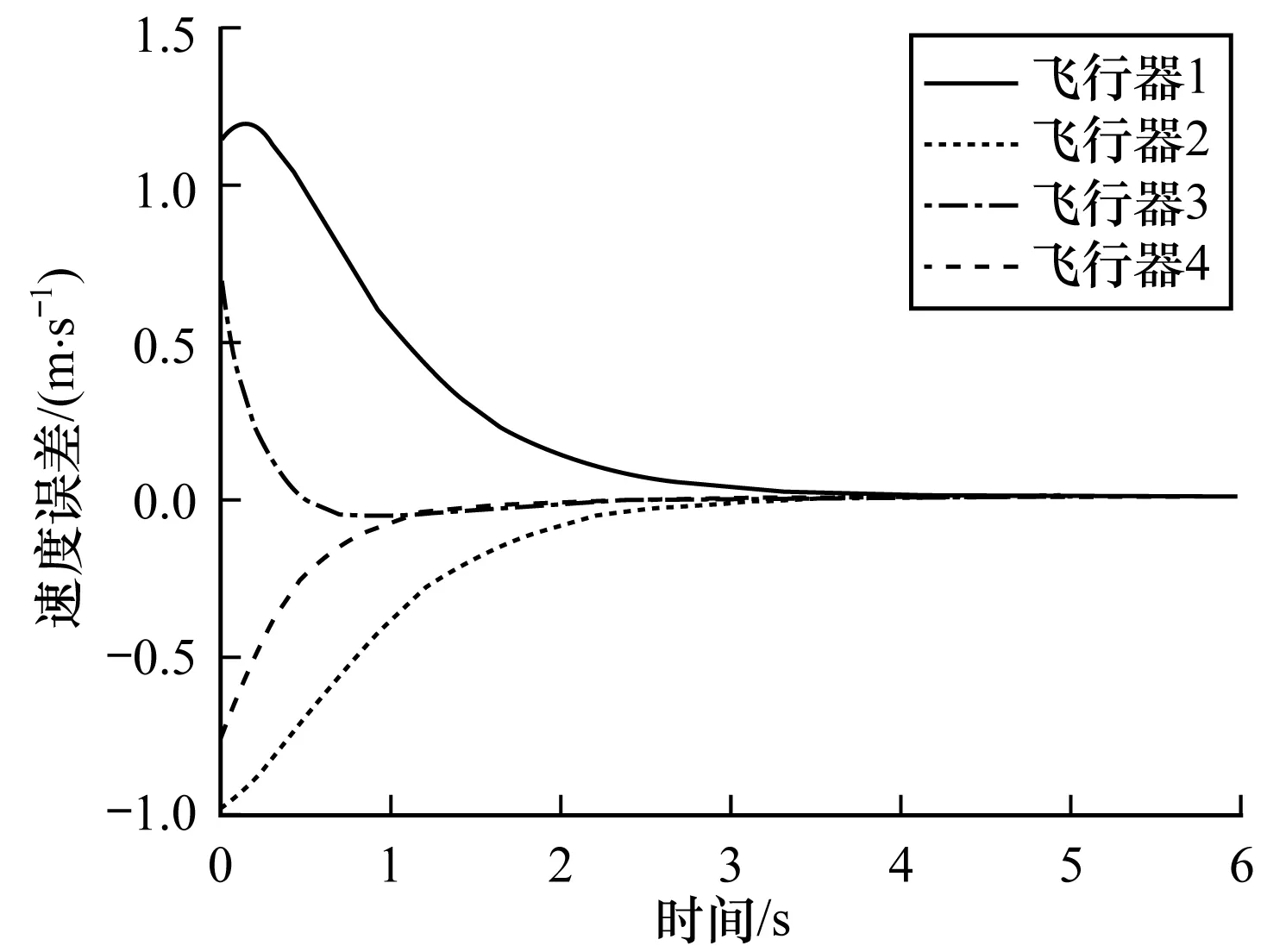
4 仿真實例分析
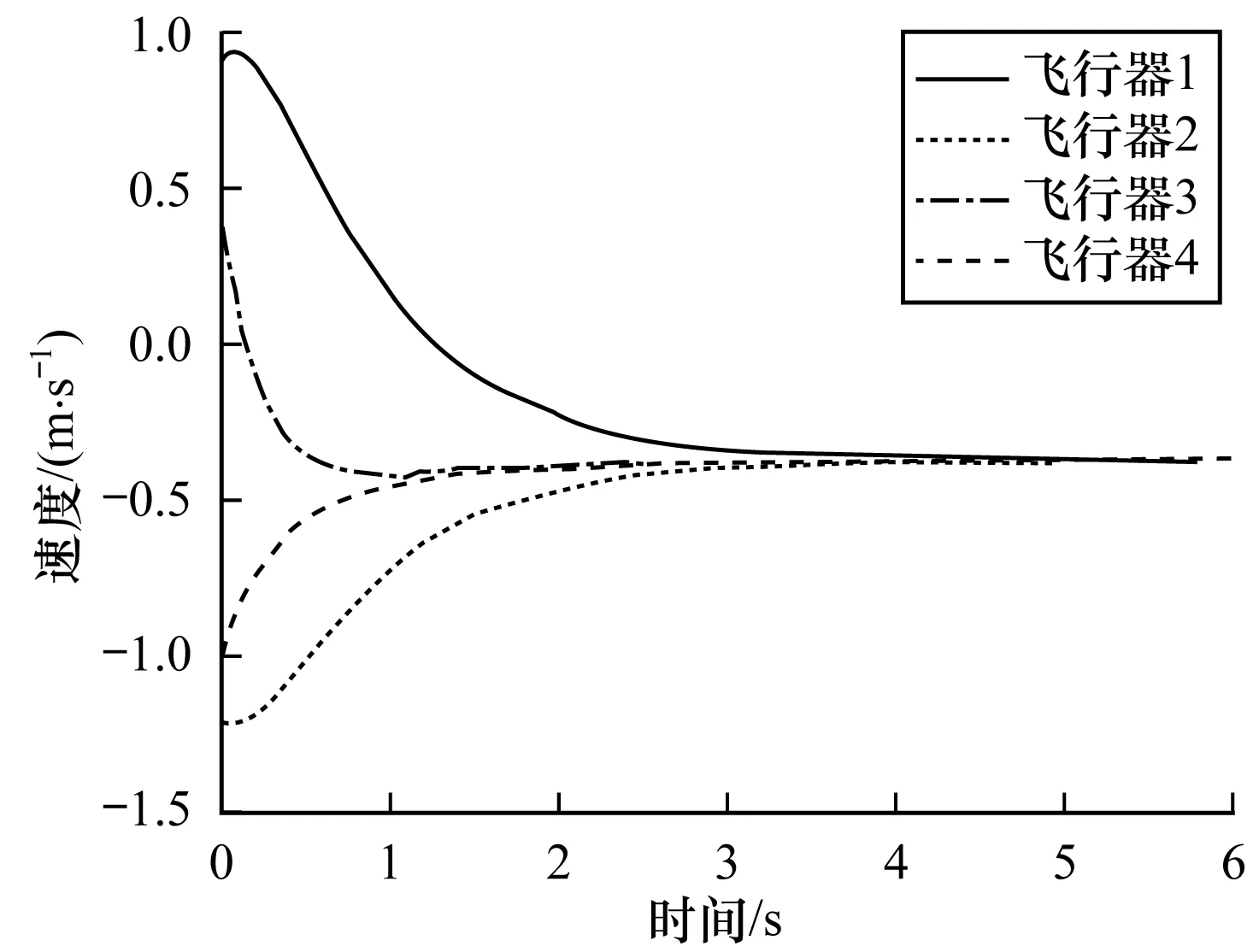
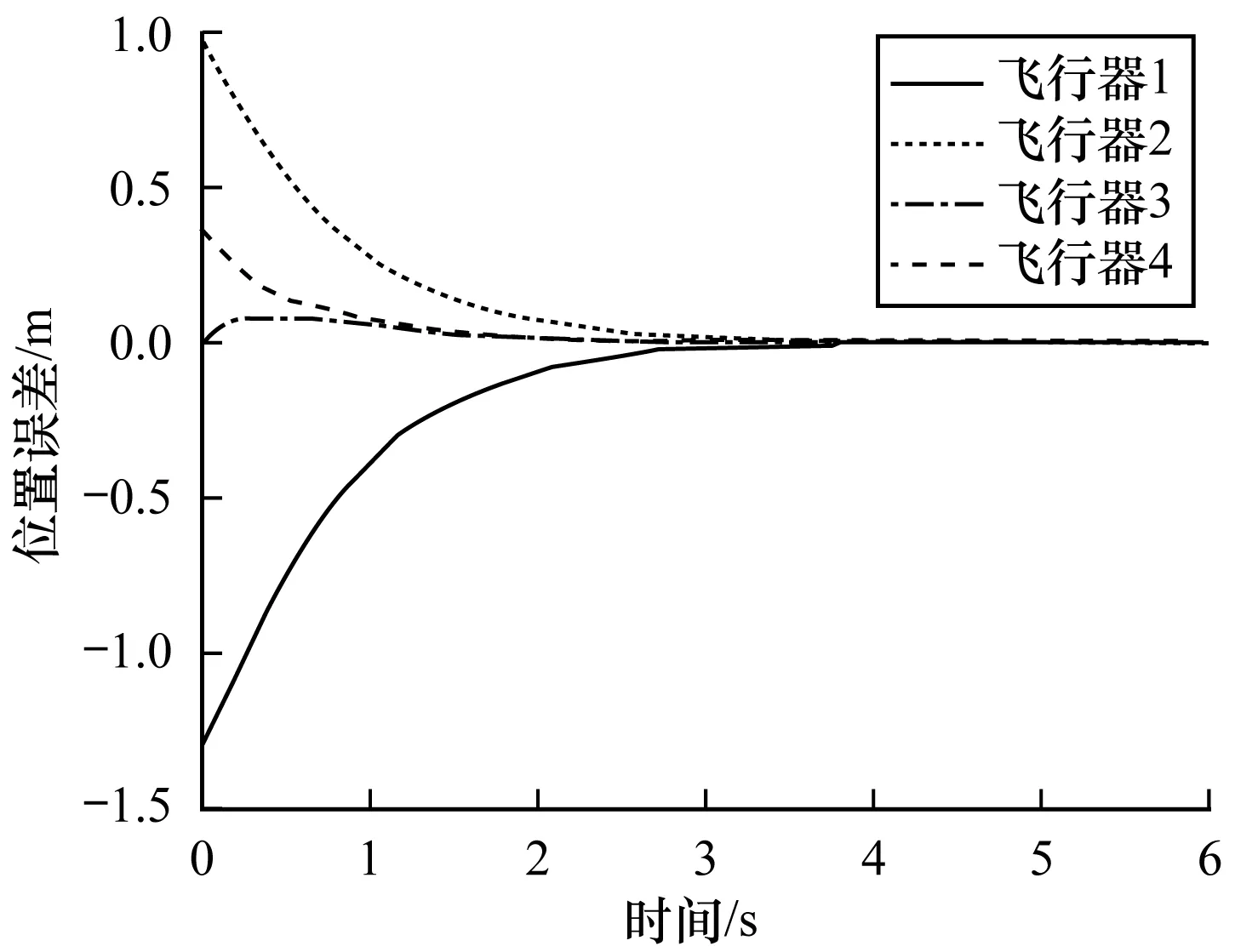

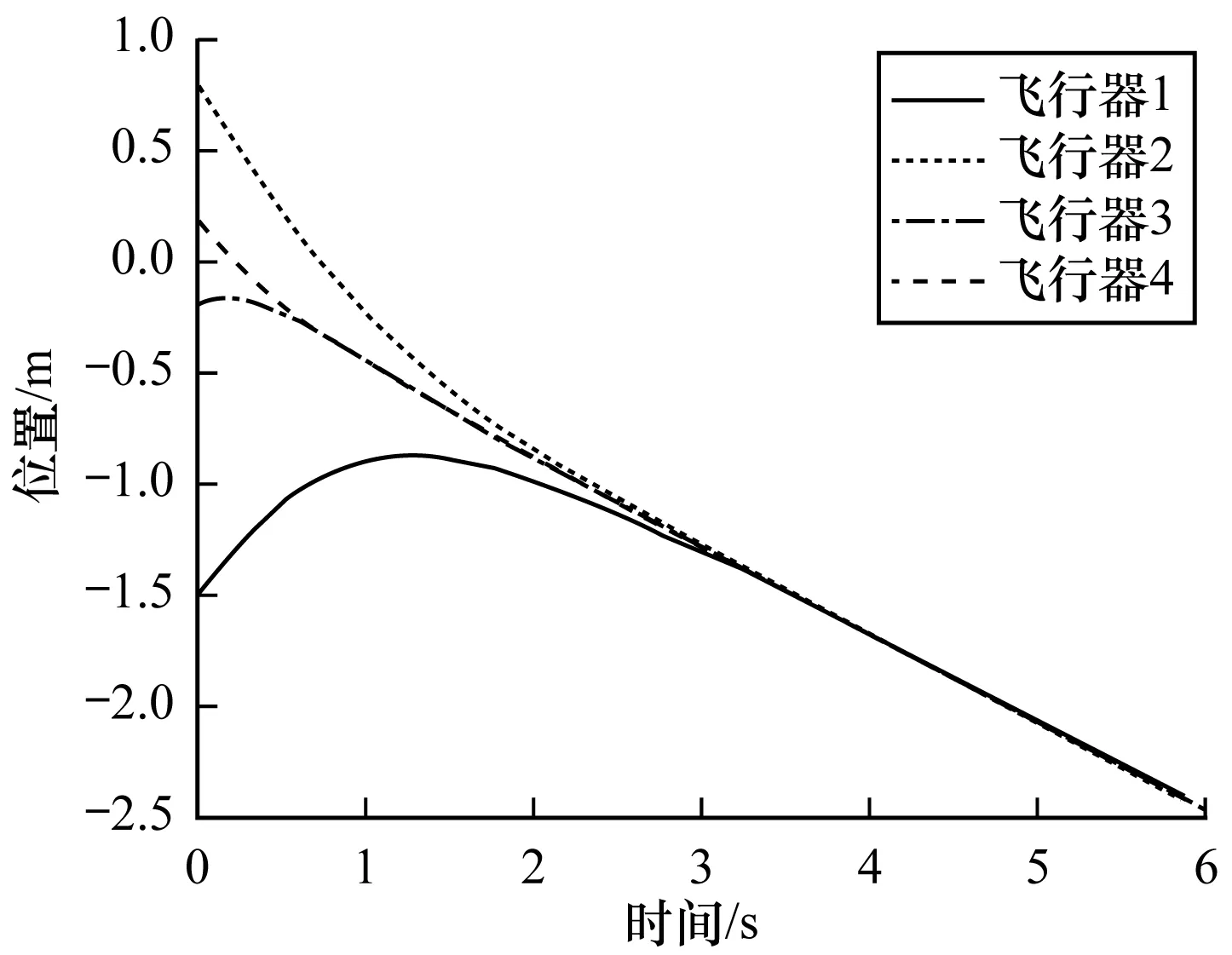
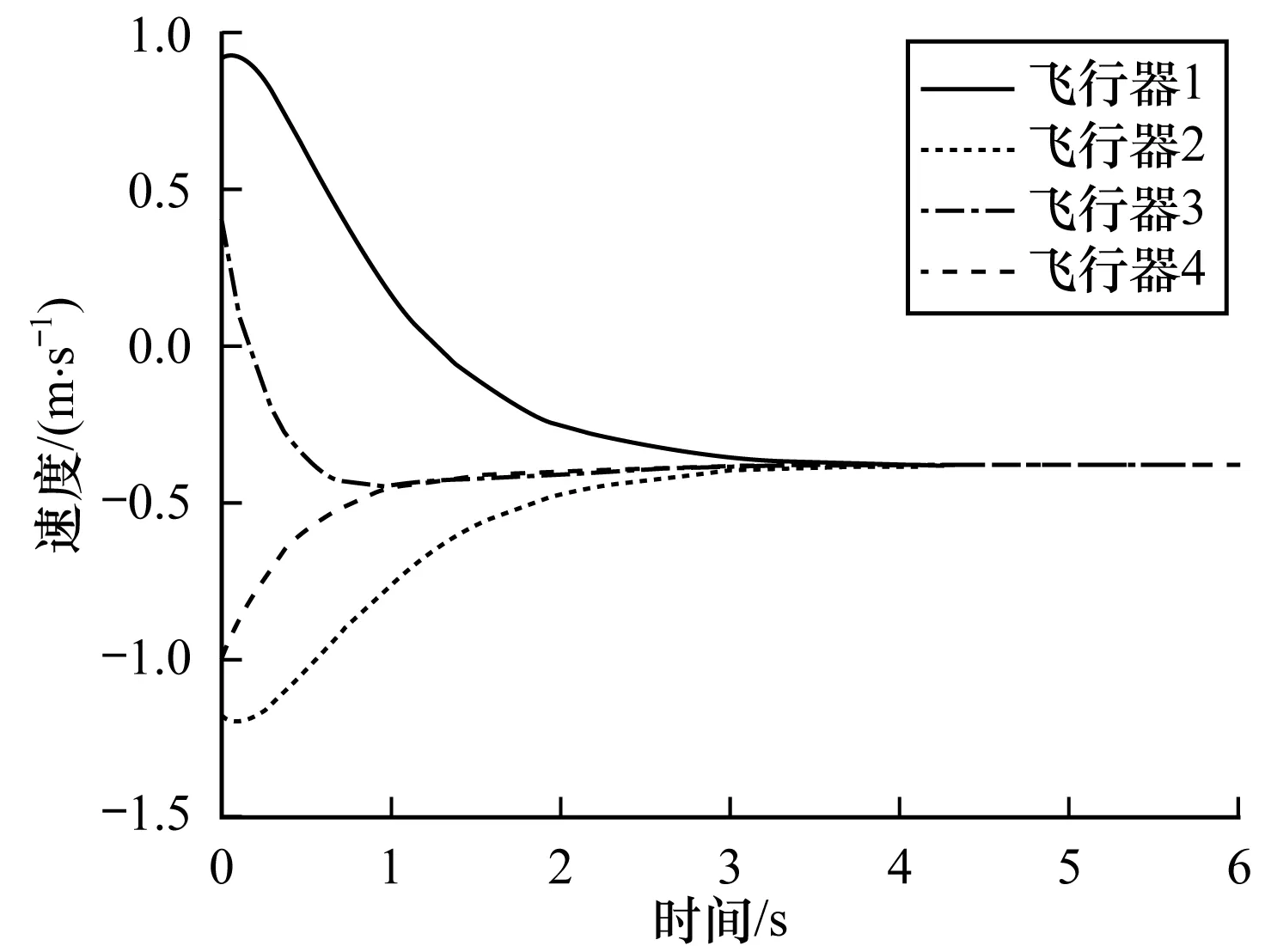
5 結(jié)束語

