空間軸對稱滲流的阻力系數法研究
朱璟赪,何思遠2,,彭天馳, 劉 韜
(1.河海大學 港口海岸與近海工程學院,南京 210098;2.西安大略大學 工程學院,加拿大 倫敦 N6A3K7;3.上海市政工程設計研究總院(集團)有限公司,上海 200061; 4.山東省交通規劃設計院有限公司,濟南 250031)
滲流計算分析方法可以歸納為基于經驗公式或解析解的簡化計算法、以有限元法[1]為主的數值分析法、室內[2]或現場試驗分析法等3類。簡化計算法采用基于萊恩法改進的直線比例法(又稱滲徑系數法)[3]、或基于丘也加夫法發展的改進阻力系數法[4]進行近似計算。
滲徑系數法,是一種沿著建筑物地下滲流輪廓線,按比例展開換算為等效水平滲徑長度,認為滲透水頭沿程均勻損失,以此進行滲流計算的簡便方法。該法沒有考慮地基滲流深度、防滲墻位置[5]等因素的影響,因此計算精度較低,適合在初步估算滲流時應用。
改進阻力系數法將閘基滲流區域按等勢線劃分為(進)出口段、水平段、內部垂直段等3種基本區段,確定基本段阻力系數,可求得各段水頭損失、滲透壓力、平均坡降,驗算地基滲透穩定性。該法避免了滲徑系數法的缺點,計算精度較高,是一種常用的簡化算法。
R.N.大衛登可夫等[6]用分段法研究了板樁基坑中的平面對稱滲流,給出了相應的阻力系數圖表。何良德等[7]研究表明,船閘閘室寬度越窄、閘墻底板或防滲設施深度越大,橫截面出流寬度的影響愈發顯著。對于等級較低、閘室寬度較小、水頭較大的船閘,應充分考慮閘室寬度的影響,防止低估出口段坡降值,不利于滲流穩定性。
在橋梁墩臺[8]、房屋建筑[9]、港口翻車機房[10]中,經常遇到圓形或類圓形基坑滲流分析問題。本文基于阻力系數法的基本原理,建立了軸對稱空間滲流阻力系數的局部計算模型,借助ABAQUS軟件計算結果繪制了進口段、出口段阻力系數曲線,通過算例驗證了本文方法的合理性和有效性,將阻力系數法應用于空間滲流分析,可提高圓形基坑工程的滲流量、滲透水頭損失、出口段坡降的計算精度。
1 軸對稱情況下的阻力系數
三維滲流量為
(1)
式中:Q為滲流量,m3/s;A為滲流斷面面積,m2;v為滲流流速,m/s;k為土壤滲透系數,m/s;J為水力梯度,又稱坡降;h為滲透水頭,m;l為滲徑長度,m。
在平面滲流問題中,可取單寬滲流量表示
(2)
式中:q為單寬滲流量,m2/s;a為單寬斷面積,m。
(3)
式中:ξ為滲流阻力系數,ξ=l/a,無量綱。在均質地基中,ξ只與滲流區域幾何形狀有關,是邊界條件的函數,與滲透系數絕對值無關。
設滲流區域可按等勢線劃分成n個串聯的典型區段,則由各區段流量相等q=qi=qj,分擔水頭hi之和等于總水頭H,可得
(4)
(5)
式中:hi為各區段水頭損失,m;ξi為各區段滲流阻力系數;H為滲流總水頭,m。
式(5)可表示為
(6)
式中:μ為滲流的流量系數,等于總阻力系數的倒數。
式(6)代入式(4)得
(7)
式中:ζi為各區段水頭分配系數,與各區段阻力系數成正比。
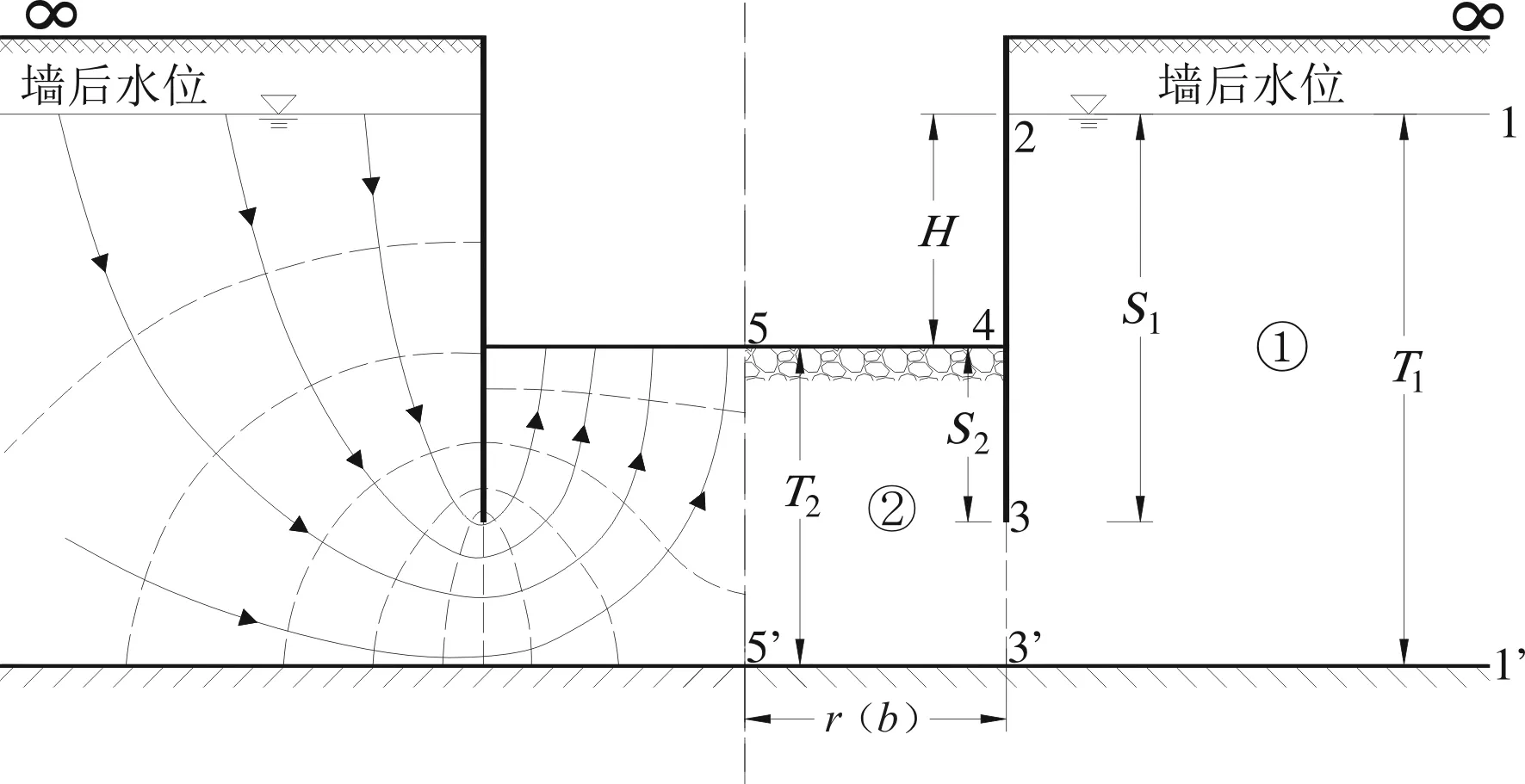
圖1 阻力系數法計算對稱板樁滲流示意圖Fig.1 Schematic diagram of symmetrical sheet pile seepage by resistance coefficient method
均質地基對稱平面滲流如圖1所示,r(b)為基坑半寬或半徑。S1為墻后水位至樁底深度,S2為板樁入土深度,T1為墻后地基透水深度,T2為基坑底下地基透水深度。假定板樁底下垂線3-3′為等勢線,將半橫斷面分為2個區段:墻后進口段①與墻前出口段②,阻力系數分別為ξ1、ξ2。
(8)
(9)
軸對稱滲流時,圖1中r(b)為板樁的圍護半徑,取單位弧長的滲流量q為
(10)
式中:Q為圓形基坑總滲流量;q為單位弧長滲流量;r為圓形基坑半徑;a為單位弧長斷面積。
同理,對于均質地基軸對稱滲流,也可分為墻后進口段、墻內出口段阻力系數。圖1中,區段①進口線1-2相對于T1可近似認為無窮長,區段②出口線4-5為平面滲流的寬度b或為軸對稱滲流的半徑r。
2 阻力系數的數值解
利用ABAQUS軟件分別建立圓形基坑進口段①、出口段②的軸對稱穩定滲流有限元計算模型,如圖2所示。只考慮基坑滲流的作用,不考慮土體的固結變形,設置土體為全約束。在1-2、4-5添加孔壓為0的邊界條件,3-3′添加梯形分布的靜水壓力邊界條件,使得透水面為等勢面,保持勢差等于1 m。其余不作孔壓邊界設置,默認為不透水邊界。
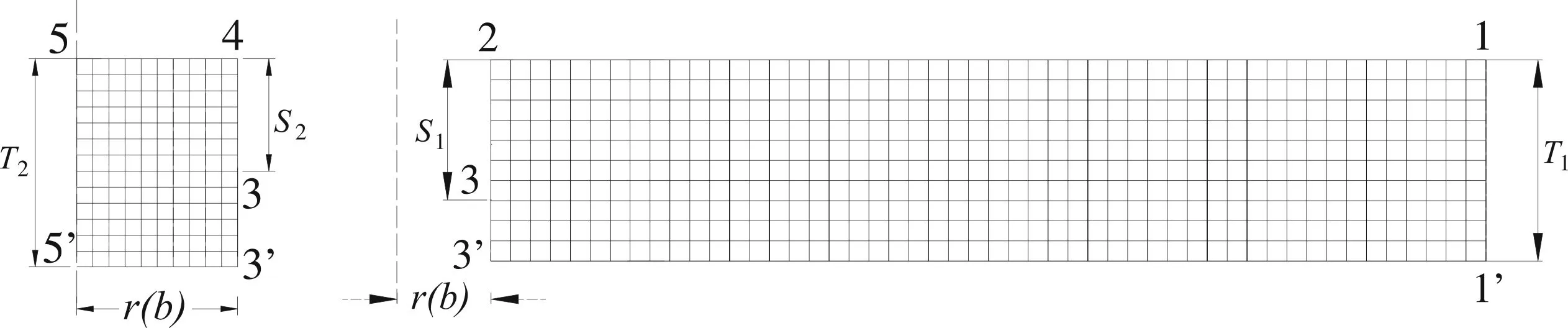
2-a 出口段ξ2 2-b 進口段ξ1圖2 進口段ζ1、出口段ζ2計算模型Fig.2 Computation model of ζ1 of inlet section and ζ2 of outlet section
采用正方形單元剖分模型。ξ1計算模型為了消除1-1′邊界條件對滲流的影響,1-2寬度取地基深度T1的5倍,豎向T1分為100層單元,水平向500列單元,在坐標系中調整2-3′與對稱距離r,模擬不同的T1/r,定義透水邊界3-3′高度,模擬不同的S1/T1。ξ2計算模型豎向T2分為100層單元,根據S2/T2調整水平列數,定義透水邊界3-3′高度,模擬不同的S2/T2。
由于進口段、出口段阻力系數ζ1、ζ2需要計算大量的工況,操作較為繁瑣,故利用ABAQUS的腳本語言Python進行參數化建模,進行穩態滲流計算分析。分別提取各種S1/T1與T1/r組合、S2/T2與T2/r組合下的總流量Q,按式(10)計算單寬流量q,再由式(9)求得ζ1、ζ2。
為了簡潔本節下文S、T的下標省略。典型的進口段ζ1計算模型等勢線見云圖3,典型的出口段ζ2計算模型等勢線見云圖4。


T/r=0.5T/r=5T/r=0.5T/r=53-aS/T=0.23-bS/T=0.8圖3 ζ1計算模型部分等勢線云圖Fig.3Partialisopotentiallinecloudmapofζ1calculationmodel


T/r=0.5T/r=1T/r=2T/r=5T/r=0.5T/r=1T/r=2T/r=54-aS/T=0.24-bS/T=0.8圖4 ζ2計算模型部分等勢線云圖Fig.4Partialisopotentiallinecloudmapofζ2calculationmodel
阻力系數ζ1、ζ2繪制成圖5、圖6或表1、表2所示,便于圓形基坑進行滲流計算時查用,T/r>10后,可以利用表1、表2的相應值外推求得。


5-aζ1~S/T5-bζ1~T/r6-aζ2~S/T6-bζ2~T/r圖5 阻力系數ζ1曲線Fig.5Curveofresistancecoefficient(ζ1)圖6 阻力系數ζ2曲線Fig.6Curveofresistancecoefficient(ζ2)
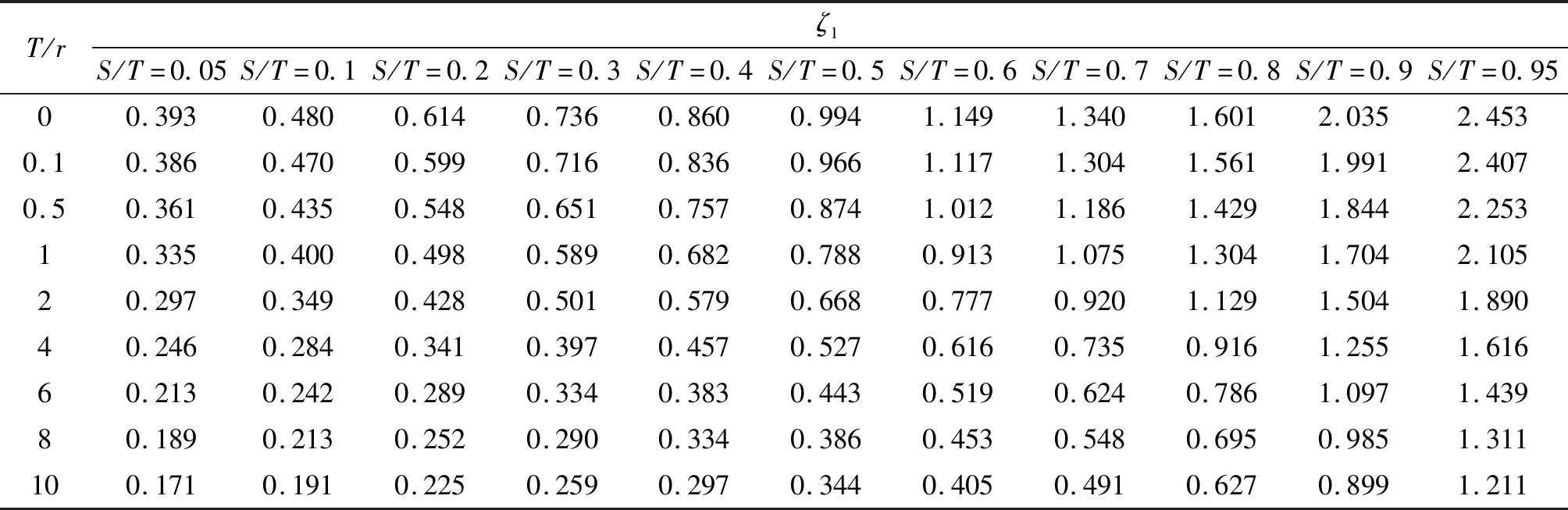
表1 進口段阻力系數ζ1表Tab.1 ζ1 of inlet section
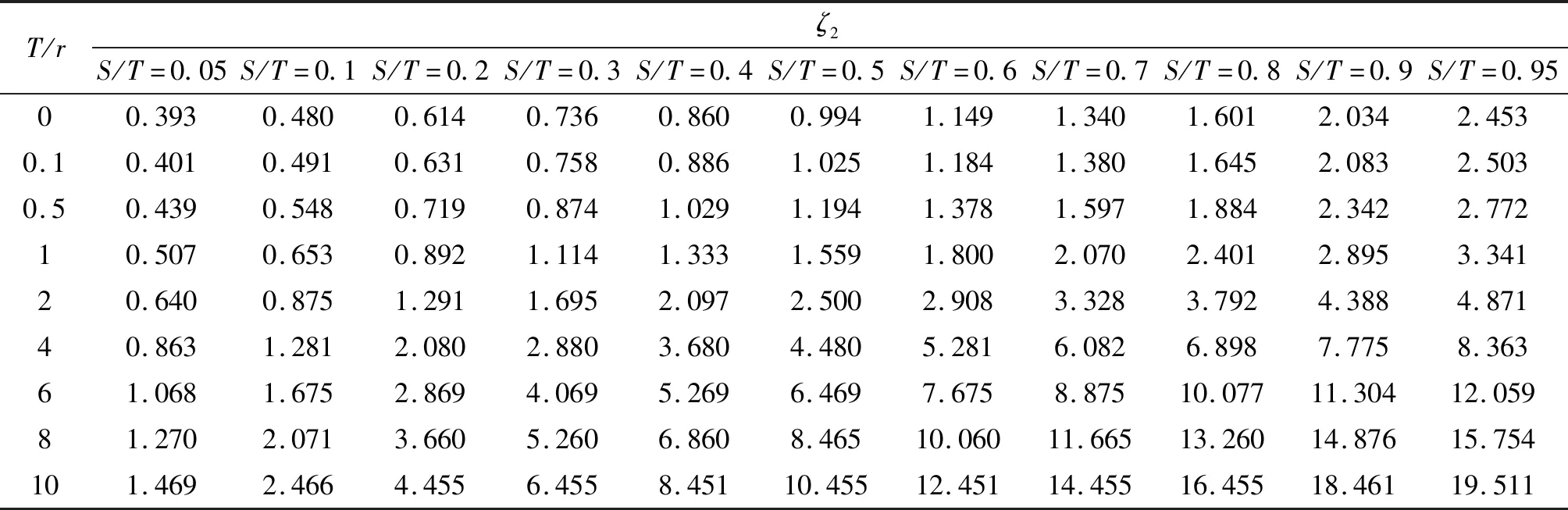
表2 出口段阻力系數ζ2表Tab.2 ζ2 of outlet section
總體來看,當T/r為定值時,阻力系數ζ1、ζ2變化規律一致。隨著S/T的增大,入滲厚度比(T-S)/T越小,此時墻體埋深相對地基計算深度越大,滲流路徑越長,阻力系數ζ逐漸增大。當S/T>0.90后,ζ曲線斜率急劇增大。理論上講,S/T=0時ζ=0,S/T=1.0時ζ=+∞。
當S/T為定值時,阻力系數ζ1、ζ2變化規律正好相反,ζ1隨著T/r增大而減小,ζ2隨著T/r增大而增大。進出口的T/r、S/T對應相同時,ζ1≤ζ2。當T/r=0,即相對半徑r/T=+∞,ζ1=ζ2。當T/r≤0.1,即r≥10T時,r相對T而言,可近似認為半徑無窮大,ζ(T/r=0.1)與ζ(T/r=0.0)的誤差在3%以內。
為便于說明,記平面滲流的進口段、出口段阻力系數[7]為ψ1、ψ2,對比分析可知,T/b=0(b=+∞)、T/r=0(r=+∞)時,ψ1=ψ2=ζ1=ζ2。事實上,b>10T、r>10T時,ψ、ζ已幾乎相等。
3 算例驗證
某翻車機房圓形基坑[11]的內徑為76 m,墻體厚1.3 m,墻體頂高程為6.5 m,底高程為-24.0 m,墻高30.5 m。坑底高程-12.65 m,透水層底高程-50.5 m,坑外水位5.5 m。r=38 m,T1=56 m,T2=37.85 m,S1=29.5 m,S2=11.45 m,S1/T1=0.527,S2/T2=0.300,T1/r=1.474,T2/r=0.996,查表1和表2內插可得ζ1=0.763,ζ2=1.112,計算的ζ=1.874,μ=0.534,ζ2=0.593。
運用ABAQUS有限元軟件[12]建立圓形基坑的軸對稱滲流分析整體模型,為了消除邊界效應的影響,模型總半徑228 m是內徑的6倍,墻后土體向外延伸190 m,約為土體厚度的3.4倍。土體單元采用軸對稱四節點孔壓單元。等勢線云圖如圖7所示,根據有限元計算結果換算得μ=0.509,ζ=1.966,ζ2=0.559。圖7表明,墻底下垂線并不是一條等勢線,但該垂線的勢差較小,約占總勢差的10%,這是引起μ計算誤差4.9%,ζ2計算誤差6.1%的主要原因。


7-a有限元模型7-b等勢線圖圖7 有限元整體模型與等勢線圖Fig.7Equipotentiallineoffiniteelementmodel
R.N.大衛登可夫等[6]進行了28次圓形基坑滲流的室內試驗,研究的參數范圍0.02 R.N.大衛登可夫由于當時沒有軸對稱阻力系數圖表,建議查閱平面分段法圖表,μ折減0.8倍、ζ2放大1.3倍。圖8、圖9中計算值總體對比來看,軸對稱μ接近平面μ,軸對稱ζ2明顯大于平面ζ2,分別對比來看,軸對稱滲流的單寬流量系數μ、水頭分配系數ζ2分別是平面滲流的0.72~1.01倍、1.08~1.42倍。如坑內外S1=S2、T1=T2,兩者的比值分別為0.53~1.0倍、1.0~1.33倍。 圖8 流量系數μ對比Fig.8Comparationofflowcoefficient(μ) 圖9 水頭分配系數ζ2對比Fig.9Comparationofwaterheaddistributioncoefficient(ζ2) (1)基于阻力系數法基本原理和分段原則,針對圓形基坑滲流特點,建立了阻力系數的軸對稱局部計算模型,給出了一系列圖表可供查用,可確定相應基本段的阻力系數,計算流量系數、出口段分配系數,用于滲流穩定性驗算;(2)T/r越小或S/T越大時,墻底下垂線的勢差越小,越接近等勢線的假設,分段阻力系數法計算精度越高。流量系數μ、水頭分配系數ζ2計算值偏于安全的,誤差一般在30%以內,平均約8%;(3)與平面滲流分段阻力系法[7]對比表明,軸對稱滲流與平面滲流的單寬流量系數μ比值、水頭分配系數ζ2比值變化幅度較大。對圓形基坑滲流不建議采用平面滲流計算。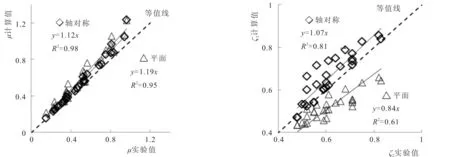
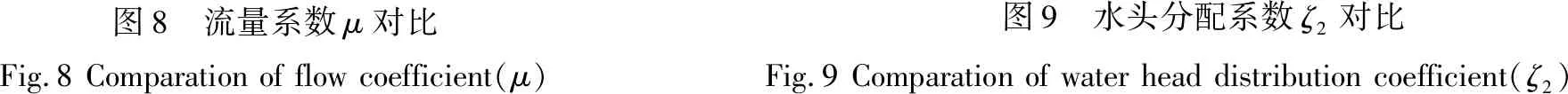
4 結論

