多軌跡段平滑過渡的前瞻插補算法①

王旭浩,張 華

(浙江理工大學 機械與自動控制學院,杭州 310018)

數控系統通常采用連續直線或圓弧對加工路徑進行逼近來完成插補.因多軌跡段的銜接處存在過渡拐角尖銳的特點,所以對離散小線段加工時,采用首位速度為零的加減速控制方式,但該方法使整個插補過程中的速度方向連續突變,即驅動軸的頻繁啟停會影響運動定位的精度.針對以上問題,張曉輝等[1]建立拐角曲線過渡模型,保證軌跡銜接處的平滑性,該算法使加工效率得到有效的提升,但不能保證加工精度;Fan 等[2]采用了基于樣條曲線插補的軌跡規劃算法,此算法參數約束少且計算速度快,但存在軌跡形狀隨速度變化而不可控的缺點.許健等[3]提出一種基于有限項正弦級數的新位置規劃算法來提高路徑過渡的速度,但速度比例參數過大會使得過渡速度很小,不利于保持速度相對穩定.關于速度規劃技術在插補算法中的應用,Hu 等[4]采用梯形加減速控制前瞻的進給速度,但存在速度和加速度曲線過渡不平滑的問題;Cao 等[5]將多路徑段細分為直線段和圓弧小線段,并對直線和圓弧軌跡的銜接處進行建模,由軌跡的位移約束條件規劃銜接點的最優速度,但前瞻處理速度時,采用對稱S 形加減速控制算法,該算法在規劃初末速度不同的路徑段時缺乏靈活性;冷洪濱等[6]采用三次多項式曲線代替復雜的S 形曲線進行速度規劃,在加減速過程中實現了加加速度的連續,但加加速度在加減速的始末位置仍然存在突變的情況.為了進一步減少系統的柔性沖擊,王允森等[7]采用了四次多項式加減速算法、寧培志等[8]采用五次多項式加減速算法,但上述算法需要大量的時間進行參數的計算,實現較復雜;史中權等[9]提出了一種加速度自適應調整的前瞻處理算法,該算法在加速度的規劃上更具靈活性,但在軌跡的拐角處未考慮平滑過渡的問題.

基于以上研究現狀,提出了一種多軌跡段平滑過渡的前瞻插補算法.該算法通過建立圓弧過渡模型進行相鄰軌跡段的銜接,并基于非對稱S 形加減速算法進行前瞻速度規劃.本文基于速度曲線擬合構造了一種新型柔性加減速算法,并基于此算法對插補運算中的歸一化因子進行求解,使加速度過渡更加平穩.最后將算法在Matlab 端和伺服系統中均進行驗證,結果表明,該算法可以使多軌跡段平滑過渡,有效優化電機運動的平穩性,提高末端執行器的精度和效率.

1 相鄰軌跡段的圓弧過渡模型

對于連續軌跡而言,任意兩直線段的連接處選用建立圓弧模型來進行拐角的平滑過渡處理[10].該算法可以根據特征點的坐標和半徑調節等參數規劃出過渡圓弧的圓心坐標、圓弧轉接點坐標和拐角等參數.

如圖1 所示,Qn,vn,rn(n=1,2,3,···)(下同)分別為初始設定的路徑目標點、速度和過渡圓弧半徑;QTn,vTn,On分別是圓弧轉接點、轉接點速度和圓心;Kn為兩圓弧轉接點連線的中點;αn和ln分別為拐角大小和角平分線;dn為分割后的小路徑段的長度.

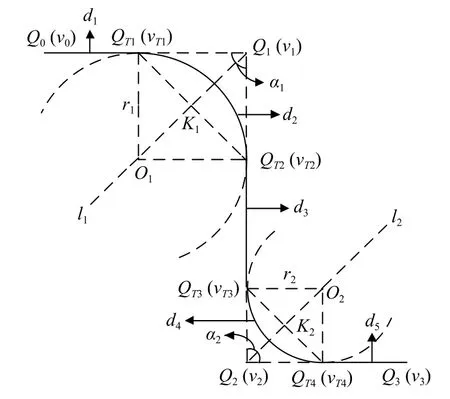
圖1 相鄰軌跡段的圓弧轉接模型

由Q0,Q1,Q2構成的路徑段轉接模型為例進行求解,設Q1坐標為(x1,y1,z1),拐角α1存在如下函數關系:

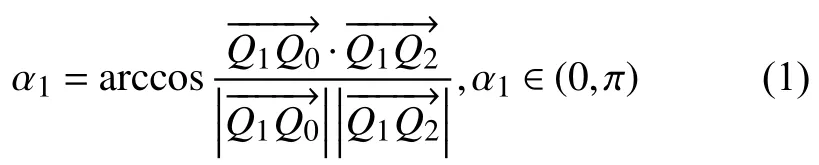
由幾何關系可得:

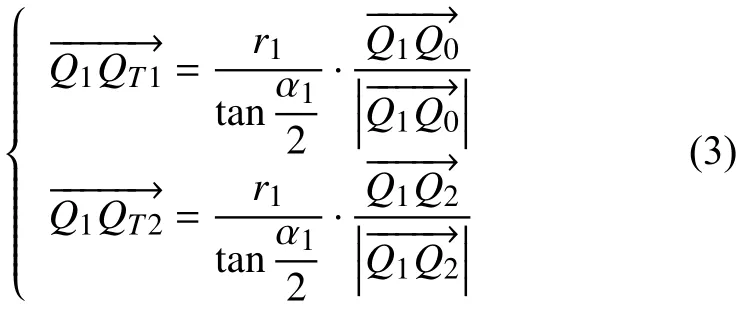
由上式可計算得出QT1的坐標(xT1,yT1,zT1)為:

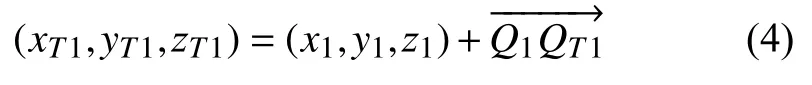
同理可以求得QT2的坐標值.由Q0和QT1的坐標可求得直線長度d1的值,因K1為QT1QT2的中點,可得:

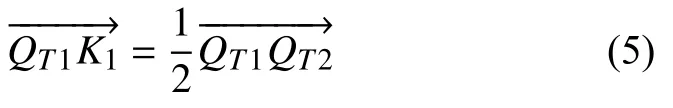
由式(5)可求得K1點坐標.由圖1 中的幾何關系可得:

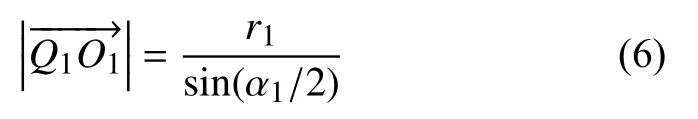
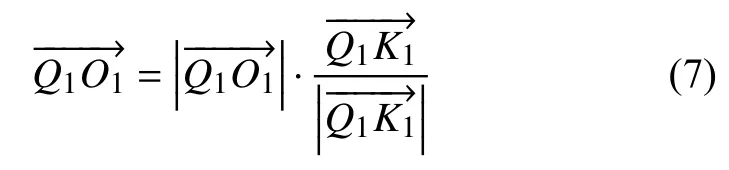
將式(6)帶入式(7)可求得O1點坐標.圓弧轉接模型的所有參數均求解完畢,剩余轉接模型可以此類推.

2 新型柔性加減速控制算法

傳統的余弦加減速算法通過余弦函數來計算出加速、勻速和減速段的執行時間和位移,該算法采用的余弦函數的計算量較直線函數要大,并沒有充分利用三角函數加減速算法和直線形加減速算法在軌跡規劃階段計算結果一致的特點來簡化計算.對此提出一種新型柔加減速控制算法,在軌跡規劃時,將直線形加減速算法代替余弦算法對加速段、勻速段和減速段的執行時間進行求解,即在插補控制時,將當前插補周期帶入余弦加減速函數中進行曲線擬合[11].此算法能使速度和加速度的過渡更加連續平滑,并減少傳統余弦加減速算法的計算量.

2.1 計算加減速段的執行時間

由圖2 知,vs為初速度,vm為勻速運行時的速度,ve為末速度,設a 和d 分別為加速段和減速段的加速度.加速段時間Ta和運行位移Sa可分別表示為:

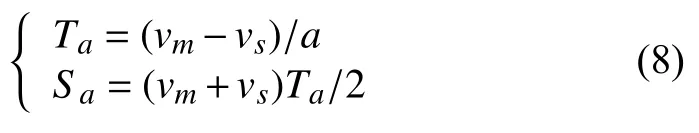
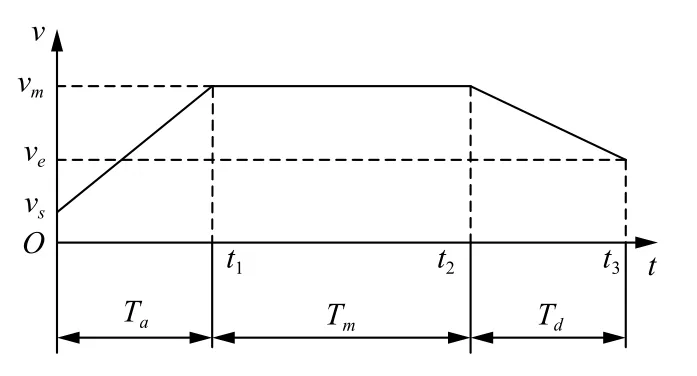
圖2 直線形加減速算法速度曲線

減速段的時間Td和運行位移Sd可分別表示為:

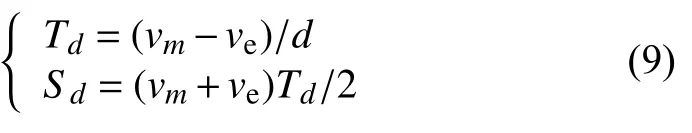
勻速段的運行位移Sm和執行時間Tm可分別表示為:

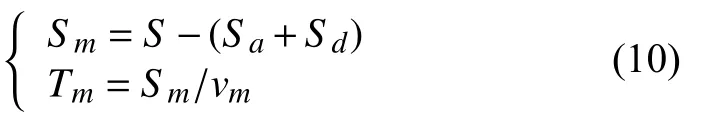
由圖2 可知:

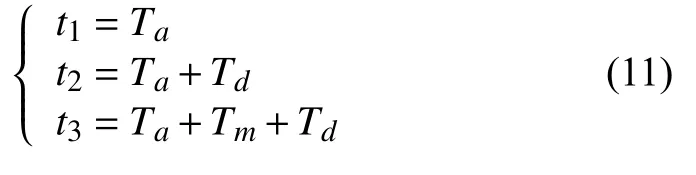
2.2 構造各速度段的位移函數

由余弦加減速算法構造加速段的速度時間函數:

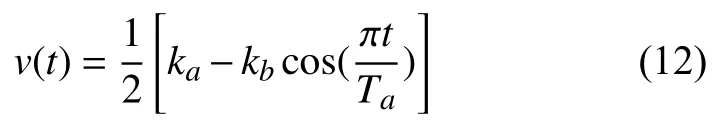
上式中,t /Ta∈[0,1],ka和kb的取值分別為:

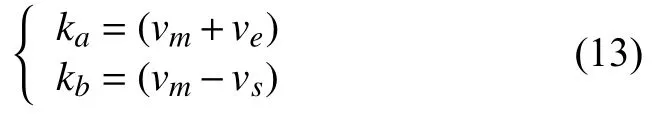
因三角函數無限可導,所以聯立式(12)和(13)連續求導得到的加速度和加加速度均連續且有界,從而提升系統的平穩性.各速度段位移函數S(t)如下：

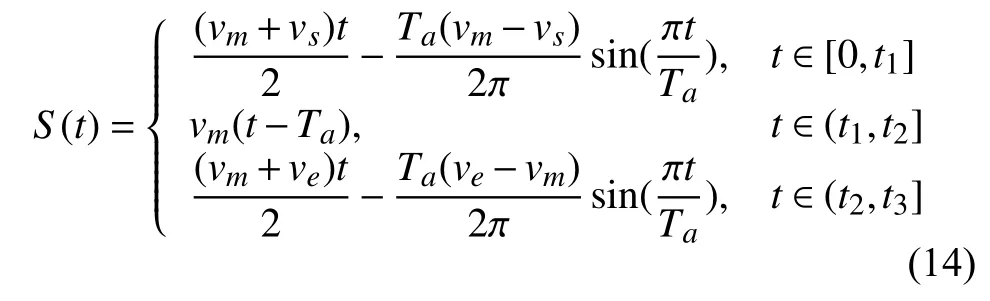
將式(8),(9)和式(10)的計算結果,帶入到(14)式中,擬合出各階段對應的新位移函數:

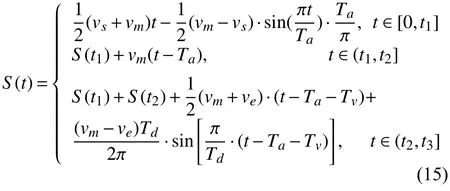
對式(15)中的各段位移函數S(t)分別求導即可得出系統對應不同階段的速度函數:

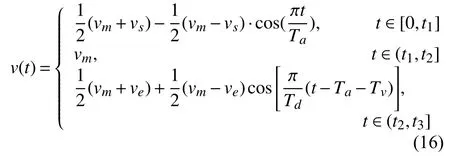
同理,對速度函數v(t)求導可得系統各段的加速度函數:

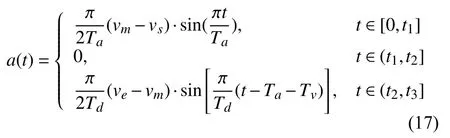
系統的穩定性分析:取式(15)～(17)中加速段的位移、速度和加速度函數構造一個非線性系統:取其李雅普諾夫函數V 為:

可知V 正定.沿系統的任意軌跡:令V 對t 求導:

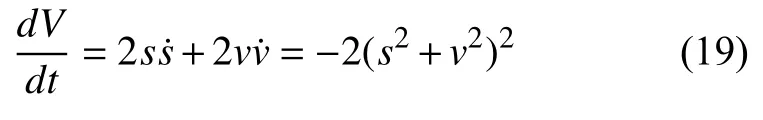
顯然上式是負定的,由李雅普諾夫穩定性定理可知:該系統是漸進穩定的.

由式(15),對各個階段位移函數積分可得:

將上式與式(8)～(10)對比可知,式(20)的結果與直線形加減速算法中的位移公式相同.這就很大程度上簡化了速度前瞻和軌跡規劃時的運算量.

2.3 基于Matlab 的仿真對比

(1)在Matlab 程序中設定同一組參數,即位移為50 mm,初速度為0 mm/s,末速度為8 mm/s,最大速度為40 mm/s,最大加速度為110 mm/s2.對傳統余弦算法和新型柔性算法的運算效率進行仿真對比.得到的運動學曲線如圖3,各速度段執行時間如表1.

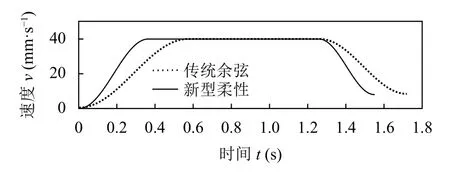
圖3 余弦算法與新型柔性算法的速度曲線

表1 兩種算法各速度段的運算時間(單位:s)

由圖3 和表1 所示的仿真結果表明:同一組參數約束下,新型柔性算法運算總時間更短,可有效減小原余弦加減速算法的運算量,提升運算的實時性.

(2)對新型柔性加減速算法、直線形加減速算法及傳統7 段S 形加減速算法進行仿真,得到的運動學曲線對比如圖4 所示.

由圖4 可知:相較于直線形加減速算法,新型柔性加減速算法的速度過渡更加平滑;相較于傳統7 段S 形加減速算法,新型算法的加速度過渡的平滑性得到有效改善,算法構造的過程更簡潔;新型加減速算法的速度曲線根據給定的參數約束條件不同而呈現非對稱的狀態,滿足多路徑段規劃時的外界約束要求.

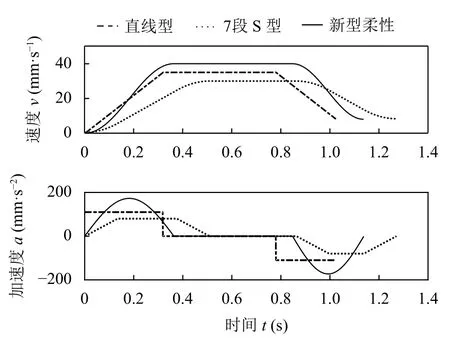
圖4 3 種加減速算法的運動學曲線對比圖

3 前瞻插補算法設計

前瞻控制技術的兩個關鍵點是加減速控制和連續軌跡段間的銜接速度處理[12,13],算法設計如下.

3.1 加減速控制算法

軌跡規劃中的速度控制部分由非對稱S 形加減速算法[14,15]進行規劃,該算法的運動學曲線如圖5 所示.

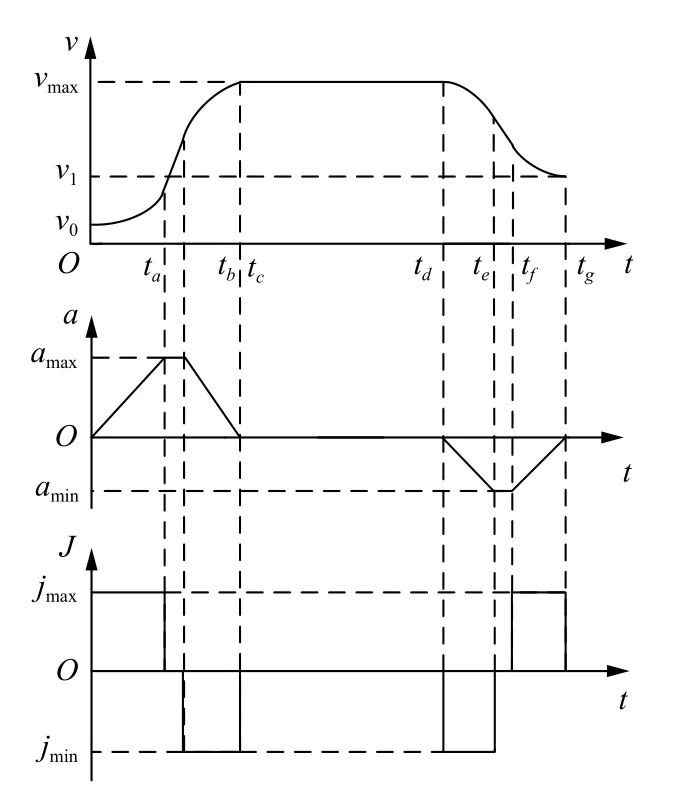
圖5 非對稱S 形加減速算法的運動學曲線

由圖5 所示的運動學曲線可知,時間ta～tg將整個速度曲線分為加加速、勻加速、減加速、勻速、減減速、勻減速和加減速7 個階段;v0,vmax,v1分別為初速度,設定最大速度和末速度;amax和amin分別是加速度的最大值和最小值;jmax和jmin分別代表加加速度的最大值和最小值.下節將按照非對稱S 形加減速算法對連續軌跡的細分小線段進行速度的規劃.

3.2 軌跡銜接速度處理

以圖1 中Q0Q1QT3構成的拐角為例,由非對稱S 形加減速控制方法將軌跡段中的直線段Q0QT1和QT2QT3進行加減速規劃,對銜接圓弧QT1QT2做勻速處理.為了使末端執行器高效率運行,將圓弧段的速度規劃為相鄰直線段的可達最大速度vlim.具體如下:

若滿足:

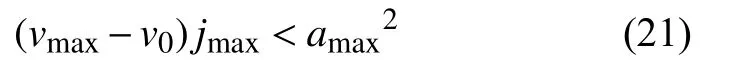
則加速段的時間Tsa可以求為:

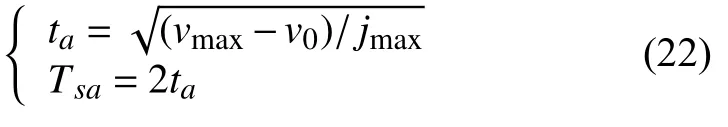
否則按下式求解:

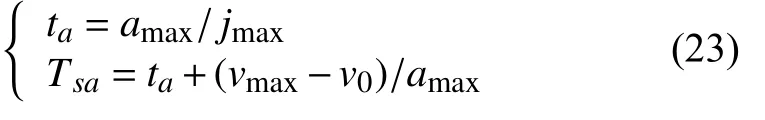
若滿足:

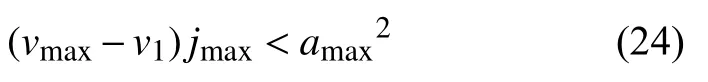
則減速段的時間Tsd按下式求解:

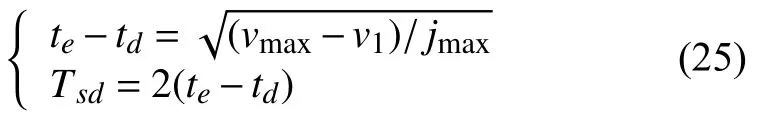
否則按下式求解:

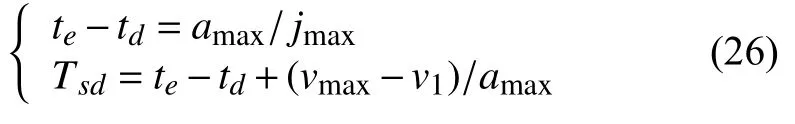
勻速段時間Tsv可求解為:

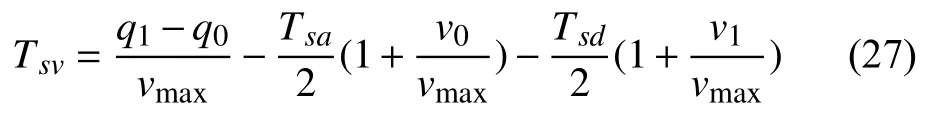
上式中,q0和q1分別代表初末位置;若Tsv＞0,即存在勻速段,則系統的限制最大速度vlim取vmax;若Tsv≤0,則vlim＜vmax.

加速直線段Q0QT1的速度與時間如下函數關系:

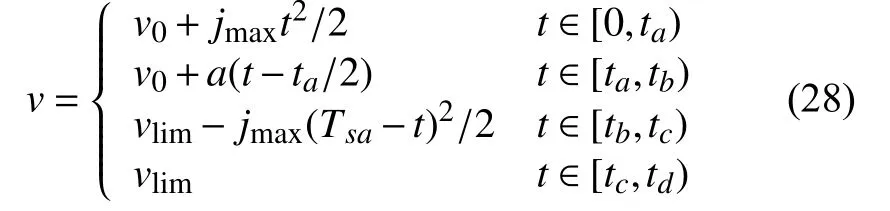
減速直線段QT2QT3的速度時間存在以下函數關系:

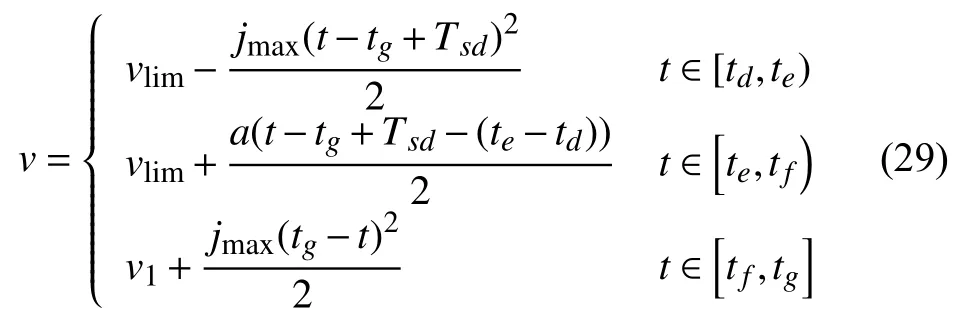
將兩直線段中間的銜接圓弧QT1QT2的速度規劃為vlim,至此,連續軌跡段間的銜接速度規劃完畢.

3.3 位置插補

以Q0QT1段為例,設起始點Q0的坐標為(x1,y1,z1).中間插值點的位置坐標(x,y,z)可以表示為:

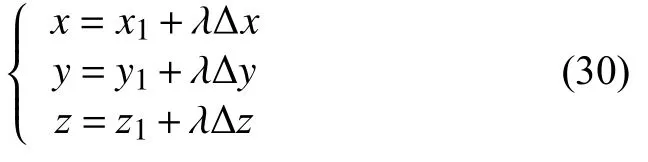
式中,λ 為歸一化因子,(△x,△y,△z)代表首末位置間的增量.故插補問題轉變為對歸一化因子λ 的求解.傳統的插補算法基于拋物線過渡的方式對歸一化因子進行求解,但規劃得出的速度和加速度曲線的并不連續,這會加劇系統振蕩.本文將采用新型柔性速度規劃算法來進行歸一化參數的求解.

為簡化算法,根據第2 節內容將新型柔性加減速算法的速度做對稱處理.設加速階段的時間為T1,位移為S1,勻速階段末端的時間為T2,位移為S2,總的運動時間為Tsum,總位移為Ssum.設末端執行器在勻速運動時的線速度為v2,基于直線形加減速算法求解各段速度的時間時,設加速度和減速度的值為a_n,則可以計算出加速階段的時間和位移分別為:

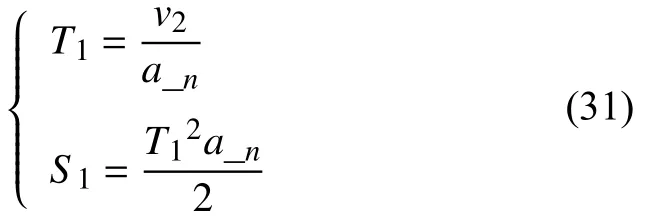
總時間Tsum為:

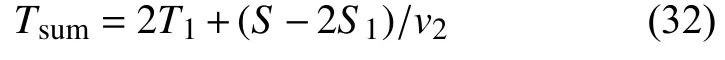
將位移、時間和加速度參數進行歸一化處理:

上式中,S1λ,T1λ,T2λ,aλ分別是S1,T1,T2,a_n的歸一化參數,結合新型柔性型速度規劃算法的位移公式,對歸一化因子λ 進行求解:

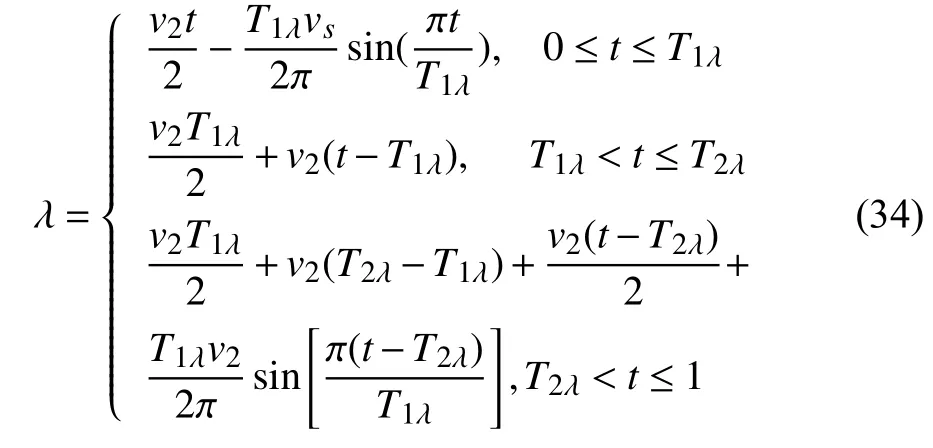
上式中,t 代表當前時刻,且t=i/N,(0≤t≤1),i=1,2,3,···,N,其中N 代表總的插值點數,通過下式來計算：

式中,Pn是插值參數,用于增加插值點數;X 和Y 在直線插補中分別表示末端執行器的總位移和線速度;在圓弧插補中分別表示末端執行器的圓心角和角速度.每個插值點的時間值,都有一個λ 與之對應,且0≤λ≤1,結合式(30)即可得到各個插值點的位置坐標.

3.4 插補算法流程

插補算法流程如圖6.

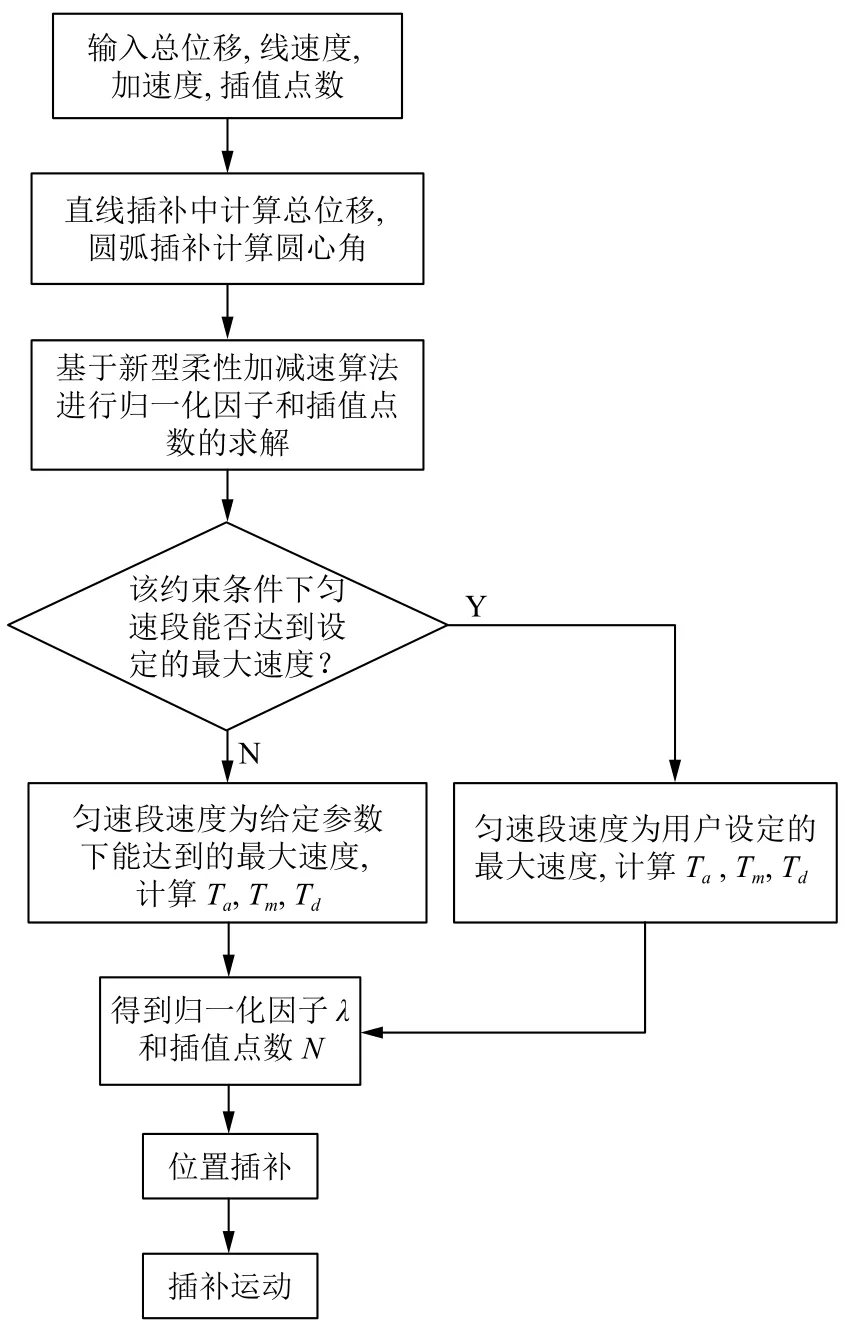
圖6 插補算法流程圖

4 實驗測試與結果分析

4.1 基于Matlab 的多段軌跡過渡實驗

設定目標曲線是由9 條線段組成的連續軌跡,給定如表2 的位置坐標、過渡圓弧段的速度參數及其半徑參數;設定系統允許的最大加速度amax=600 mm/s2,最大加加速度jmax=3000 mm/s3,插補周期為0.002 s,將以上參數初始化并進行空間插補運算,對比傳統算法和平滑過渡前瞻算法得到的軌跡效果及運動學曲線.

表2 實驗一給定實驗參數

方法一:傳統算法采用多軌跡段初末速度為零的加減速控制方式.由方法一規劃的空間軌跡效果如圖7 所示;其的運動學曲線如圖8 所示.

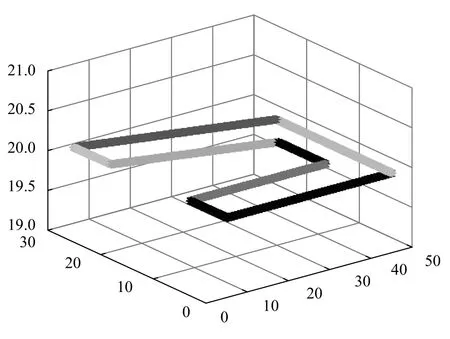
圖7 傳統算法規劃的空間軌跡

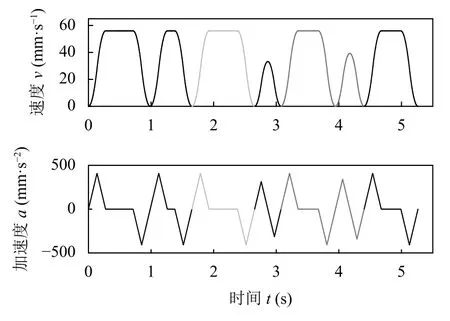
圖8 傳統算法規劃的速度和加速度曲線

由圖8 中的速度曲線可知,傳統的控制方式存在頻繁啟停的問題,容易引起振動并對運動軸造成沖擊.基于方法一計算得到的總執行時間為5.2636 s.

方法二:采用多軌跡段平滑過渡的前瞻算法,過渡圓弧半徑設為r=3 mm,其余參數同方法一.由方法二規劃的空間軌跡效果如圖9 所示;其運行學曲線如圖10 所示.

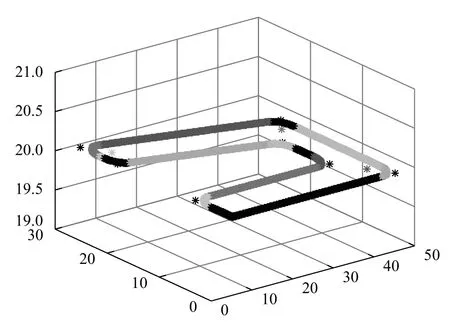
圖9 平滑過渡前瞻算法規劃的空間軌跡

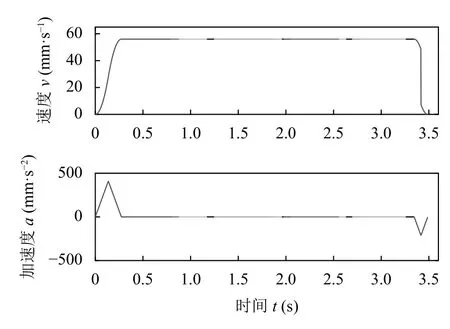
圖10 平滑過渡的前瞻算法規劃的運動學曲線

對比圖7 和圖9 可知,由方法二規劃得到的軌跡輪廓過渡的更加平滑;對比圖8 和圖10 可知,速度前瞻插補算法將過渡圓弧的速度規劃為相鄰直線段能達到的最大速度,提升了末端執行器速度的連續性和平穩性;基于方法二計算得到的總執行時間為3.4877 s,相較于方法一,該算法將執行效率提升近33.8%.

4.2 基于工控機的測試與分析

實驗平臺(如圖11)的上位機采用研華的工控機,處理器是intel(R)Core(TM)i5-4460,CPU 頻率是3.20 GHz,系統內存為8 GB.上位機軟件TwinCAT 通過EtherCAT總線實現TwinCAT 和伺服驅動器的實時通信,并可以完成人機界面的搭建.按表3 將規劃后的位置坐標下發給伺服驅動器,速度和加速度數據由機械手末端電機的編碼器進行采集,并在上位機界面中實時顯示.

在上位機軟件中進行程序編寫和設定參數.設定最大加速度amax=600 mm/s2,最大加加速度jmax=3000 mm/s3,插補周期為0.002 s.實驗通過限制拐點處不同的最大速度來檢驗加減速控制的平穩性,并分析過渡圓弧的半徑參數對于插補效率的影響.由編碼器采集的三組半徑參數對應的數據繪制而成的速度和加速度曲線分別如圖12 和圖13 所示.

表3 初始化參數

由圖13 可知,在設定最大加速度為600 mm/s2時,電機的最大加速度為378 mm/s2,表明本文前瞻算法在速度的約束下,對加速度做出了自適應的調整,證明了算法的可行性;由圖12 和圖13 可知,當拐角半徑參數設定為1.6 mm 時,系統的運行時間為6.9251 s;當半徑設定為4.2 mm 時,系統的運行時間為6.8409 s;當半徑設定為7.3 mm 時,系統的執行時間為6.7273 s,系統的執行時間隨設定半徑參數的變化而變化.

圖11 實驗平臺示意圖

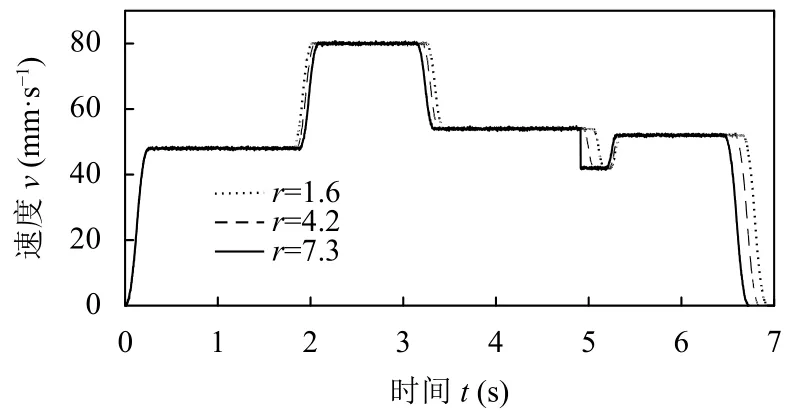
圖12 規劃的速度曲線

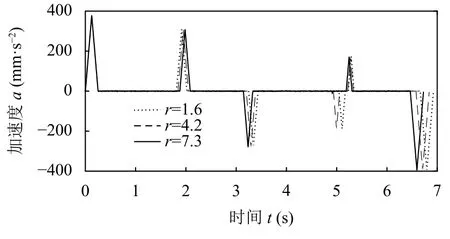
圖13 規劃的加速度曲線

本實驗結果表明:

(1)在不同的速度約束下,前瞻插補算法可以自適應調整速度和加速度,保證了速度過渡的平穩性;

(2)因多軌跡段之間靠圓弧銜接,所以每段軌跡規劃的初末速度不必減小為零,即不存在電機頻繁啟停的問題,有效的提升了加工效率,驗證了該前瞻算法的對每小段軌跡銜接速度處理的有效性和優越性;

(3)本文算法對參數設定進行了簡化,用戶可在上位機界面設定半徑參數對目標軌跡做理想的修形處理,也可根據插補效率隨過渡圓弧半徑參數的不同而不同的特點,設定最優的半徑參數來使系統的加工效率最大化;給定的速度和加速度參數可作為算法應用硬件平臺的最大限制速度,進而防止軌跡形狀因速度變化而出現不可控的缺點.

5 結論

多軌跡段平滑過渡的前瞻插補算法能夠使插補輪廓曲線更加圓滑,有效解決了傳統多軌跡段初末速度為零的加減速控制方式帶來的頻繁啟停問題,并且用戶可以調節半徑參數對軌跡進行修形處理;該算法采用的速度前瞻技術可以規劃出多軌跡段銜接圓弧的最優速度,并實時計算下一插補周期的執行速度,使末端執行器的運動具有連續性,有助于提高機床的實際運行效率;在插補算法的設計中,相較于基于拋物線過渡和傳統余弦過渡的插補算法,基于新型柔性加減速控制算法的空間插補算法對于速度和加速度的連續性均有穩定的提升,適用于精度要求較高的場合.