自調節步長果蠅優化的自適應密度峰值聚類①

鄧然然,李 偉,楊榮新

(長安大學 信息工程學院,西安 710064)

聚類是一種常用的屬于無監督學習的數據處理方法,由聚類所挖掘出的信息可以為進一步深入地分析數據提供理論基礎[1].聚類采用定量數學思想,按照數據間的相似程度將其歸到幾個群,其結果滿足各個群內相似性較強,而各群體之間相似性較小的特點.同一組樣本有時會因為不同的目的、數據輸入方式、所選的分群特征或數據屬性,形成不同的分群結果.聚類是數據挖掘的重要手段[2],聚類算法分為:劃分聚類、層次聚類、密度聚類、網格聚類、圖論聚類等[3].

快速峰值算法是2014年6月Rodriguez Alex 在Science 上提出的一種新型聚類算法,該算法能自動選出樣本的類中心,而且能克服一般方法對數據要求的缺陷,可以實現對非球形數據進行高效聚類[4].該算法選定聚類中心:1)較大的局部密度,即中心點相鄰點的密度值均小于該點;2)與其他密度更高的點之間的“距離”較大.DPC算法原理簡單、聚類高效[5],在各個領域都有廣泛的應用[6,7],例如應用于高速公路收費數據分析[8]及異常事件挖掘[9]等.然而,通過聚類算法的評價[10],DPC算法的缺點也十分明顯,需要根據經驗值設定參數截斷距離;需要根據計算出的局部密度以及距離兩個值生成用于選擇聚類中心的決策圖,并人為在其中選取這兩個值都較大的點為聚類中心.這種選擇存在較高的主觀性與不穩定性,嚴重影響后續非中心點的分配、優化以及噪聲點的發現[11].

現今為止,已有多種改進的DPC算法,例如:K 近鄰密度峰值聚類[12-14],結合K 近鄰的概念重新定義截斷距離和局部密度的度量方法,避免截止距離的人為設置;基于果蠅算法的密度峰值聚類[15-17],利用果蠅優化算法得到最優截止距離,進而完成對局部密度和與密度更高的點的距離的計算;布谷鳥優化的密度峰值快速搜索聚類算法[18],利用布谷鳥優化截止距離,引入余弦相似度原理,將方向與實際距離相結合,能夠更好的劃分邊界區域內的數據點;除此之外,還有熱擴散密度峰值聚類[19]、自適應聚合策略優化的密度峰值聚類算法[20]等等.但是現有的改進算法仍有改進的余地.

果蠅優化算法(Fruit fly Optimization Algorithm,FOA)是一種新的群體智能方法[21,22],通過迭代搜索尋找最優解.與此同時,已有諸多學者致力于改進FOA算法,例如新型改進果蠅優化算法[23]、改進的變步長果蠅優化算法[24]、改進步長與策略的果蠅優化算法[25]等.但是果蠅優化算法還存在許多不足.

本文引入改進的自調節步長果蠅優化算法[26],該算法根據當前濃度差值變化率,對步長進行相應調整,用過迭代計算,得到最佳截止距離.本文以更高的效率與準確率的得到這一關鍵參數,并計算密度與距離的乘積,根據乘積值自適應的選出備選聚類中心,再從備選聚類中心中,以同一類僅有一個中心為原則選出真正的聚類中心,然后對其他非中心數據點進行分配,最后通過類的邊緣區域對聚類結果進行優化.

1 算法原理

1.1 密度峰值聚類算法

DPC算法主要分3 個步驟進行:計算距離矩陣、選取聚類中心、剩余點的分配及優化.

1.1.1 計算距離矩陣

密度峰值算法的輸入為待處理數據點的距離矩陣,即每個點之間相似性.在進行距離計算之前,首先將原始數據的不同字段進行標準化處理,使各維度的數據具有相同的量級;然后計算數據間的距離,最后輸出距離矩陣.本文選取歐幾里得方式來計算距離d (xi,xj),并輸出為若干行、三列的矩陣,其中前兩列表示兩個數據點的序號,第三列為前兩列表示的兩個數據點之間的距離,例如矩陣的第1 行為:1 號數據、2 號數據、1 號2 號數據間的距離,第2 行為:1 號數據、3 號數據、1 號3 號數據間的距離,以此類推,與此距離矩陣即為快速峰值算法的輸入.

1.1.2 聚類中心的選擇

聚類中心的特征是局部密度大而且與其它密度更大的點相距很遠.

某點的局部密度 ρi是以截止距離為半徑的圓內的點的個數:

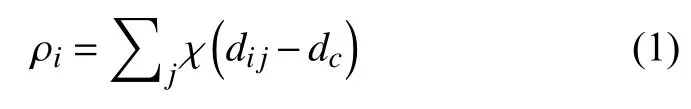
式中,i 與 j為兩個互異的數據點,當a 小于0 時,χ(a)=1,反之χ (a)=0.dij為i 點與 j 點之間的距離,dc為截止距離,由用戶根據經驗值設定.一般而言 dc的選取原則為:將距離 δi按遞增方式進行排序并編號,找出所有距離個數的1%～2%所對應的序號,將dc設置為該序號對應的距離值.

某一數據的δi值被定義為:

對于密度最高的點,由于不存在更高點,故將其δi值定義為該點與其余所有的數據之間距離的最大值.

計算出各點的這兩個量之后,將所有的數據點以ρ 和 δ 作為兩個維度進行可視化輸出,所輸出的圖形稱為決策圖.

1.1.3 非聚類中心點的分配及優化

在找到聚類中心之后,確定類的數量,然后合理分配剩余點.分配原則是:每個剩余點逐個被分到與其距離最近的有較高密度的點所在的類簇,且此操作以單步執行,直到把所有的點全部分配到對應的類為止.

一般的聚類方法優化都是以使目標函數在每一次的迭代中達到最優為原則而實現的.本文提出的算法中優化的方法為:先為每個類劃分一個邊界區域,邊界區域的定義是分配給某一類簇的點距離另一類簇的點的距離小于截止距離 dc;接著在每個邊界區域內找出密度最高的點并標記其密度為 ρb,遍歷類內的各個點,密度大于ρb的點被分到類內,反之被標記為噪聲.

1.2 自調節步長果蠅優化算法

1.2.1 果蠅優化算法

FOA 模仿果蠅搜尋食物源,果蠅通過嗅覺可以輕易的捕捉到范圍內目標源散發的氣味,然后利用其視覺進行追蹤,不斷的更新果蠅群位置,逐漸靠近目標源.算法的主要步驟如下:

1)初始化種群:

果蠅數量為 Size_num和算法所需循環執行總次數Max_times.在確定活動區域中隨機給定果蠅群體一個起點Start_X,Start_Y.

2)給每個果蠅個體隨機的方向與距離,用嗅覺尋找食物:

3)計算果蠅到坐標原點的距離 Di以及味道濃度判別值Si:

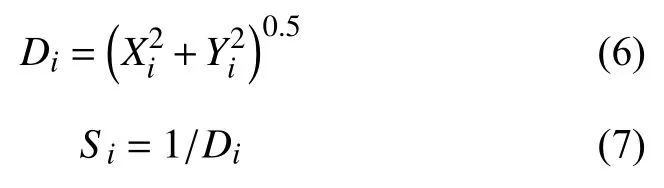
4)將濃度判別值 Si帶入判定函數 Function(Si)求出其Smell_i,此處判定函數為使用果蠅優化算法對某一函數求解最優解時的判定函數,根據實際被求解函數而定:

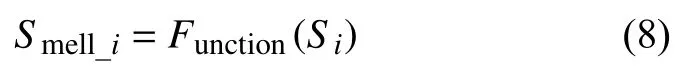
5)找出群體中濃度最優的果蠅(本文以最小值為最優解):

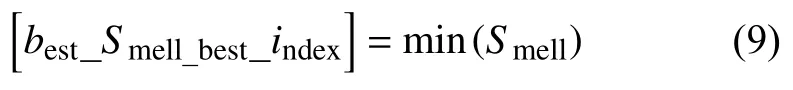
6)保留最佳濃度值Smell_best與其坐標,果蠅群體根據視覺飛往最優位置:

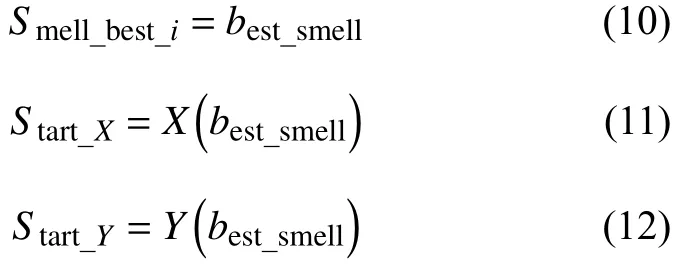
7)迭代尋優:重復步驟2)、3)、4)、5),判斷:Smell_best_i ＜Smell_best_i-1,如果上式取值為真,則轉到步驟6),否則繼續迭代進行優化.

1.2.2 自調節步長果蠅優化算法(SFO)

傳統的FOA算法的搜索半徑是固定不變的,即每一代果蠅以固定步長隨機在尋找食物.在算法迭代開始時,較大的步長有利于全局搜索尋優,而且可以有效的跳出局部最優.但是,尋優后期,較大的步長會導致較弱的局部搜索,可能會錯過最佳值,同時收斂精度也會減小.較小的步長雖然可以提升收斂度,但是在迭代前期降低了尋優速率.傳統的FOA算法難以權衡全局搜索能力和局部探索能力,自調節步長果蠅優化算法根據濃度差值變化率的大小對步長進行動態更改;并且在改變步長過程中引入指數與三角函數機制,使步長變化具有非均勻性和隨機性.在迭代初期為了加快全局搜索速率,適當增加步長值,迭代后期為了能讓算法能對局部進行精細搜索,適當減小步長值,該算法針對原果蠅算法的全局尋優速率慢和局部收斂精度不高而做出了改良.算法的主要改進步驟如下:

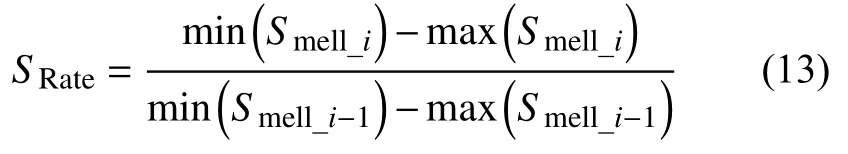
本文將最小值設為最優值,將最大值設為差值.由圖1 可以看出果蠅尋優迭代前期的濃度差值變化率變化較大,需要適當增加步長加快全局尋優,而隨著進入迭代后期,濃度差值變化率變小,逐漸趨近于1,并穩定在0.7～1.3 的范圍內,說明果蠅群體距離食物源已經非常靠近,濃度波動較小,這時需要減小步長,以提升精確度.

2)步長改進:根據SRate的 取值范圍,對步長進行相應的修改:

如果SRate≤0.7 或 者SRate≥1.3:

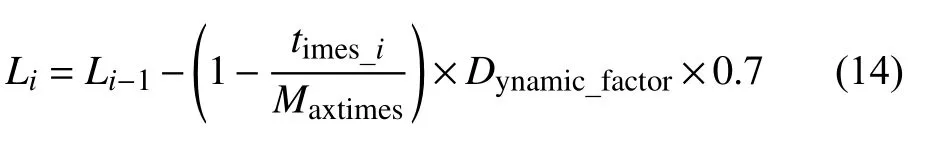
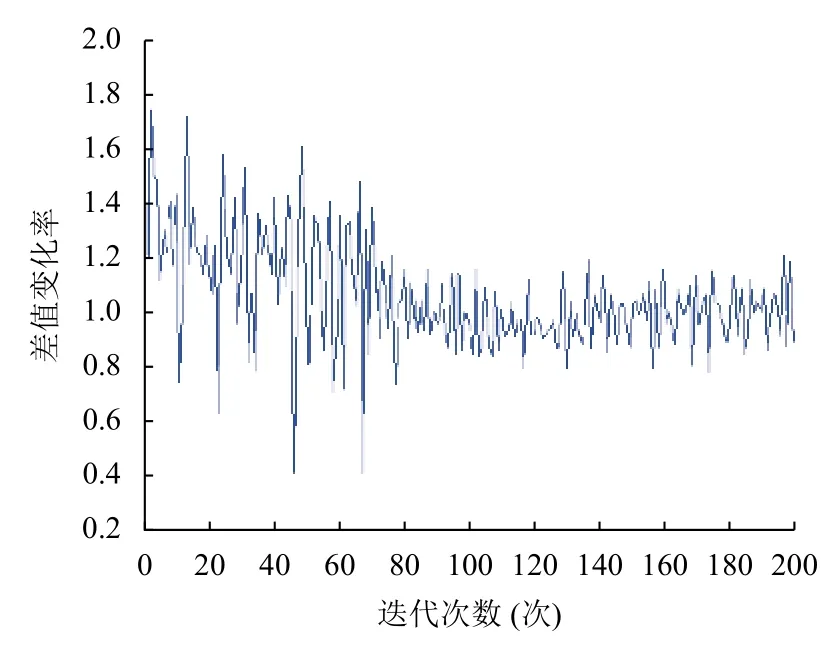
圖1 濃度差值變化率

步長調節因子:

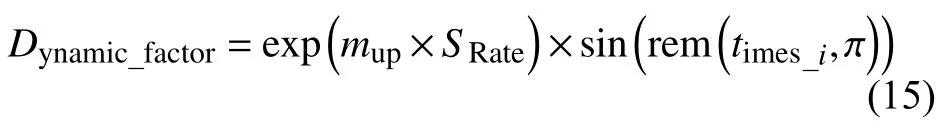
如果0.7 ＜SRate＜1.3:

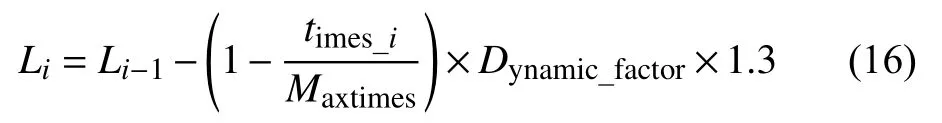
步長調節因子:

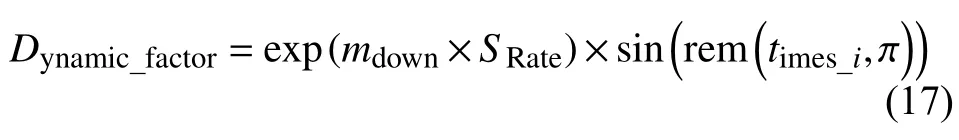
式中,Li與Li-1分別為當前果蠅尋優迭代步長和上一次果蠅尋優迭代步長;mup和mdown分別在不同所屬濃度差值變化率時所采用的步長動態變化參數,需要增大步長時采用 mup(取值大于1,本文取1.3),需要減小步長時采用mdown(取值為(0,1),本文取0.7);times_i為當前執行算法所處的運行次數;Maxtimes為算法所需循環執行次數的最大值.根據每次求的濃度差值變化率 SRate,確定其所屬范圍,對步長進行相應的修改.

圖2 為步長調節因子在取值連續的情況下所顯示的結果.指數機制可以使步長變化具有非均勻性,在果蠅尋優迭代過程中,如果濃度變化較大,那么要適當增加步長,非均勻變化的步長相對于原果蠅算法中的固定步長更容易捕捉到最優值,有利于全局搜索.

3)果蠅個體位置計算:

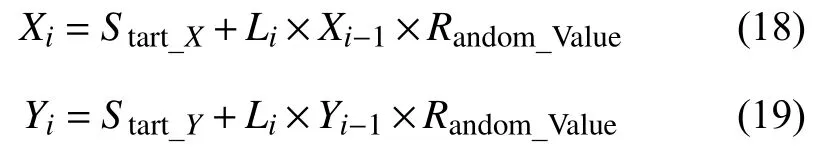
當濃度差值變化率較小時,濃度變化率比較穩定,這時候果蠅迭代尋優可能進入兩種狀態,第一種狀態是進入迭代后期,要適當的減小步長進行局部探索,第二種狀態是果蠅尋優迭代陷入局部最優化,那么引入三角函數機制是利用三角函數變化的特性,使得步長變化隨機,提高了算法跳出局部極值的能力.

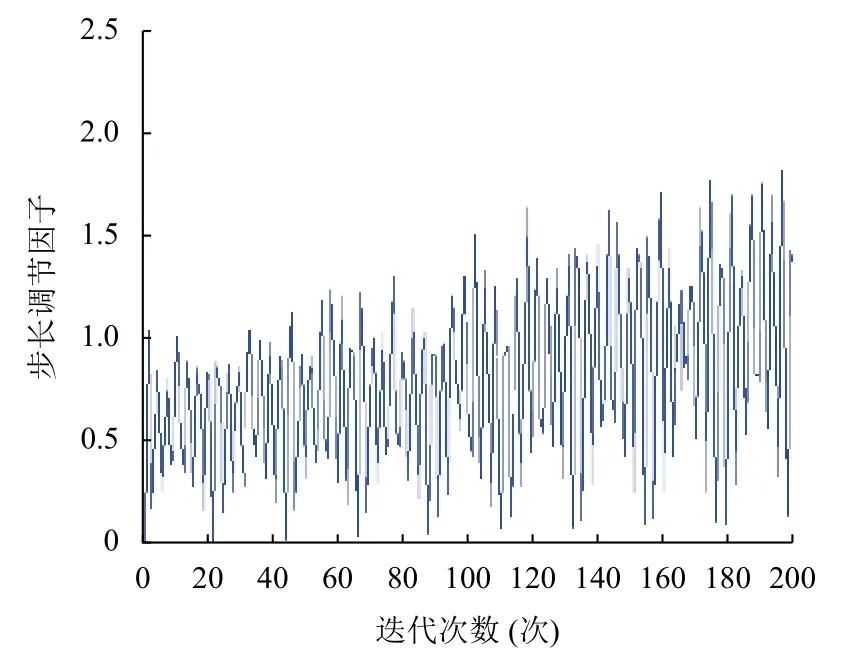
圖2 步長調節因子變化曲線

在同樣設置種群規模為20,最大迭代次數為1000 時,對比FOA 和SFO 的測試性能,采用平均值代表平均精度值,方差代表測試穩定性.對于不同的測試函數,FOA 在多數猜測是函數下未能達到理想精度,容易陷入局部最佳,SFO算法均達到了目標精度,且方差相對較小,證明本文算法具有更好的穩定性和優越性.

1.3 基于自調節步長果蠅優化的自適應密度峰值聚類算法

1.3.1 信息熵

信息熵為系統不穩定性的度量.已知空間中的數據集 D ={x1,x2,···,xn}包含n 個數據,每個數據的密度函數值為:

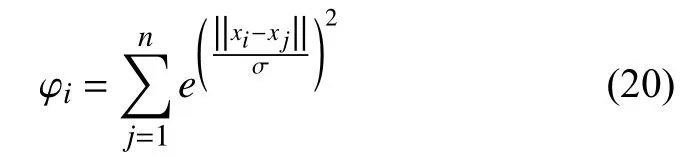
則密度估計可以定義為:

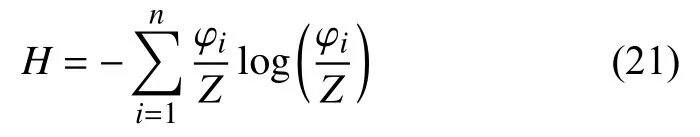
1.3.2 基于自調節步長果蠅優化的自適應密度峰值聚類

對小規模數據集進行聚類時,密度峰值聚類算法采取指數方式計算數據密度,計算公式如下:

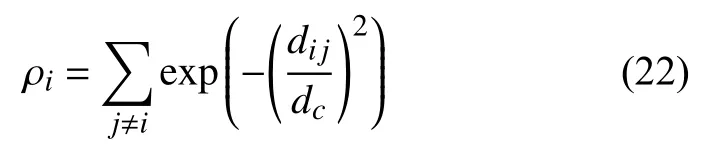
對比式(20)、(22)發現,如果選擇高斯核函數進行每個數據點密度的計算,截斷距離參數dc與σ 具有的意義是統一的,優化 σ本質上就是對截斷距離參數dc的優化.而且,若將整個數據集看成一個系統,一個好的聚類結果是系統最穩定,數據間關系確定性最好的狀態,因此,以信息熵最小值為判定依據,利用FOA算法的全局尋優特性,對 σ進行優化,優化后得出的σ 值即為最優的截斷距離參數dc.

將式(21)所示的信息熵函數作為自調節步長果蠅優化算法的濃度判定函數 Function(Si)進行優化,求出最優 σ值,即截斷距離dc.按式(1)～(3)計算得到ρi和δi后,自適應的選擇聚類中心.

聚類中心的 ρi和 δi兩 個值都較大,本文引入γi

則 γi較大的點,就很有可能是聚類中心;換言之,聚類中心的 γi一定較大,可以先挑出 γi值較大的點,在從中去選擇真正的聚類中心.將 γi值按降序排序.定義臨界點 P ,表示γ[1～P]與 γ[P～n]變 化程度最大的點,本文用γi值降序排列圖的斜率來表示其變化程度,則P 服從以下條件:

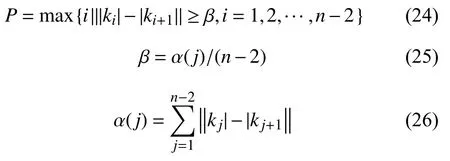
式中,ki表示第i 個點和第i +1個點之間的線段的斜率;α(j)表示在γi值降序排列圖中兩個鄰居點的斜率差的總和;β表示斜率差的平均值;i是斜率差大于等于均值β的點中序號最大的點及臨界點.

那么聚類中心就可能存在于式(27)表示的范圍內,稱這個范圍內的點為偽中心.

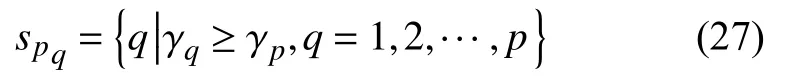
在同一范圍內存在多個偽中心,因此需要將同一范圍內多余的偽聚類中心排除.在密度峰值算法中,聚類中心與密度點更高的點相距較遠,因此,本文取同一區域中的第1 個偽中心作為聚類中心,判斷其他的偽中心到該點的距離,若小于d (xi,Nk(xi))則將其消除;如果大于,則將其作為新的聚類中心.在聚類過程中自適應的根據實際數據選出聚類中心,聚類中心個數即為最終聚類數目.

1.4 算法流程及復雜度分析

1.4.1 算法流程

?

1.4.2 算法復雜度分析

假設果蠅群體大小為S,最大迭代次數為M,個體濃度跟新計算量為O(1),計算濃度差值變化率所需的時間復雜度為O(M),并且動態調整步長的時間復雜度為O(M),所以計算最優截止距離部分的時間復雜度為O((N+2)*M).假設由自調節步長果蠅優化的自適應密度峰值聚類算法(Adaptive Density Peak Clustering based on Fruit fly Optimization of Self-adjusting stepsize,SFO-ADPC)處理的數據集有N 個數據點,則存儲每個數據點與其他點的距離的時間復雜度為O(N2),計算每個數據點的局部密度及距離所需的時間復雜度為O(2N),計算邊界區域需要的時間復雜度為O(N2).綜上,本文所提算法的時間復雜度為O((N+2)*M+(N+1)*N).

2 實驗與結果分析

2.1 實驗數據集

為測試所提SFO-ADPC算法的準確性和有效性,本文選擇了5 個人工數據集和5 個常用于聚類測試的真實數據集.表1 中為本文所用數據集,包括環形、月牙形、聚集、火焰、螺旋形、Iris、Wine 和Soybean 數據集.5 個人工數據集的數據分布情況如圖3 所示,圖中數據點橫縱坐標均為數值,無具體物理意義,故無單位.

聚集和火焰數據是典型的聚類算法性能測試數據,環形、月牙形和螺旋形數據為測試算法能否準確地對非球形數據聚類的典型數據集.Iris 是鳶尾花卉數據集,其中有150 個樣本,屬于3 個類別,每個類別有50 個樣本,每個樣本具有4 個屬性,即花萼長寬以及花瓣長寬.3 個類別分別為Setosa,Versicolour 和Virginica.Wine 是酒數據集,有178 個樣本,每個樣本有13 個屬性,屬于3 個類別,每個類別數量不同.Soybean 數據集是大豆疾病數據集,包含47 個數據,每個數據包含35 個屬性,分為4 類,是線性可分的,其所有屬性都可作為分類屬性.Ecoli 數據集是大腸桿菌數據,由336 個樣本組成,每個樣本有7 個屬性,分為8 類.Seeds 數據集包含210 個樣本,每個樣本有7 個屬性,每個樣本分為3 個類.

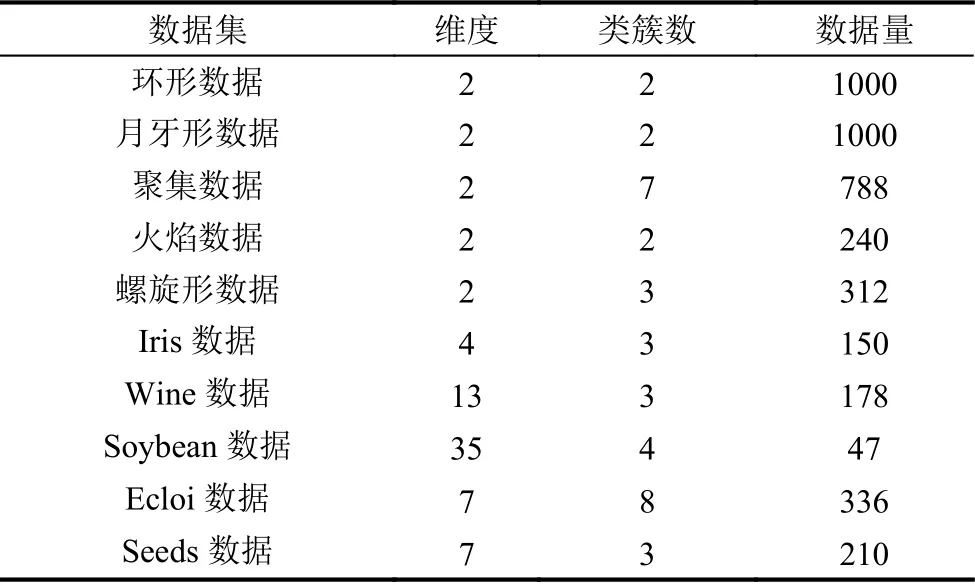
表1 實驗數據集

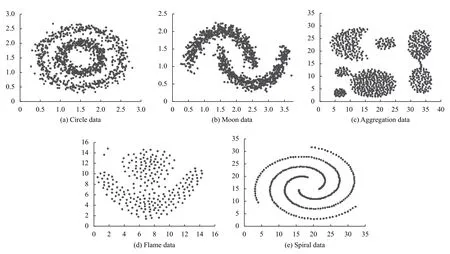
圖3 原始數據集

2.2 實驗數據集

本文主要使用兩個評價指標來測試所提的算法:內部輪廓系數(Silhouette)和外部F 值(F-measure).

1)Silhouette 指標

對于其中的一個樣本點 i來說,需要計算兩個量:a(i)與 b (i),

那么i 向量輪廓系數就如下式:

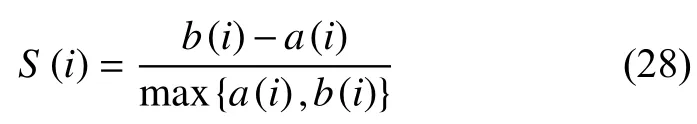
a(i)i:向量與同一類中每個點的不相似性的平均值.

b(i)i:向量與其他類的點的不相似性的最小平均值.

使用所有數據S 平均值評估簇的緊密性和可索引性.S 介于-1 和1 范圍內,對于同一數據集,S 越大聚類越好.

2)F-measure 指標

F-measure 是一種結合準確率和召回率的外部評估指標.對于真實類 Pj與聚類所產生的類Ci,分別定義準確率P (i,j)和召回率R (i,j).其表示為:

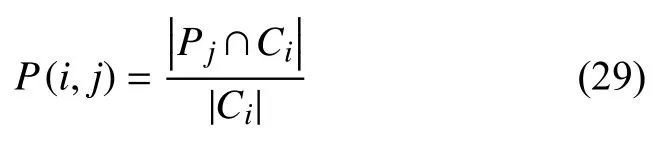
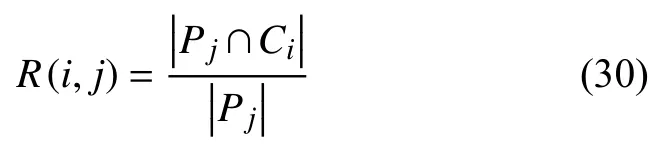
P(i,j)和R (i,j)的都介于0 和1 之間,且兩者的數值大小與相對應的正確率和召回率成正比.

相應的F-measure 指標計算:

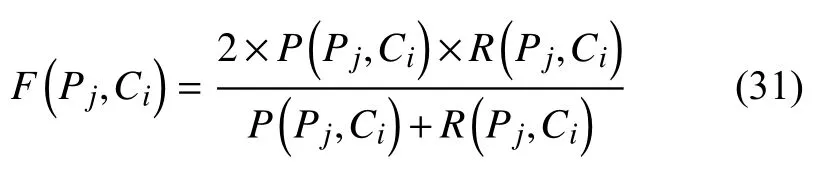
將各類F-measure 指標作平均則可以求出最終Fmeasure 值,其表示為:

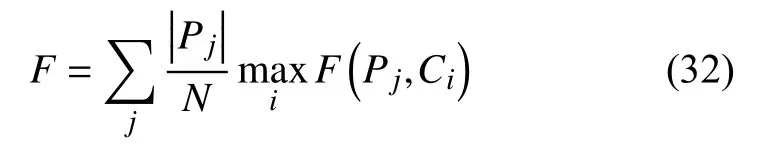
上述公式中N 為數據總個數,計算所得F-measure值越大,則算法準確程度越高.

2.3 實驗結果與分析

本文將所提算法SFO-ADPC 與FODPC、DPC、DBSCAN、K-Means 在數據集上比較.圖4 中分別為K-Means 在環形、月牙形、聚集、火焰、以及螺旋數據集上的聚類結果,圖5 中分別為DBSCAN 在環形、月牙形、聚集、火焰、以及螺旋數據集上的聚類結果,圖6 中分別為DPC 在環形、月牙形、聚集、火焰、以及螺旋數據集上的聚類結果,圖7 中分別為FODPC在環形、月牙形、聚集、火焰、以及螺旋數據集上的聚類結果,圖8 中分別為SFO-ADPC 在環形、月牙形、聚集、火焰、以及螺旋數據集上的聚類結果.

圖4 K-Means算法聚類結果

測試算法中使用的數據集分布大多為非球形的,K-Means 無法準確對其進行聚類,同時,聚集數據集雖然是球形分布的,但由于樣本量分布不均勻,K-Means仍然無法達到最好的聚類效果.DBSCAN 可以有效地對測試數據集進行聚類,但其參數確定過程較為繁瑣,不同的數據集的聚類參數相差較大,用戶需要花費大量的時間用于調參.

DPC 及其改進算法可以有效對非球形數據進行聚類,同時聚類的準確率大大提高,FODPC 及本文提出的SCFO-ADPC 給出了更好的截斷距離,克服DPC 需要人工設置截斷距離的缺陷;同時,本文算法提供的截斷距離更好,提升了聚類準確率.并且,本文所提算法能夠自適應的選擇聚類中心,改善了原始DPC算法需要手動選取聚類中心的缺陷.

表2 中列出了上述5 種算法在5 個人工數據集及5 個真實數據集的聚類效果評價得分.

圖5 DBSCAN算法聚類結果

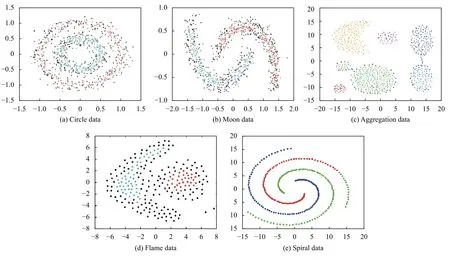
圖6 DPC算法聚類結果

圖7 FODPC算法聚類結果

圖8 SCFO-ADPC算法聚類結果

上述5 種聚類算法應用于實際數據時,SCFO-ADPC的準確率及召回率更高,本文所提算法能有效的對任何形狀的數據進行聚類,對于具有較高維度的數據集也可有效進行聚類,并且聚類效率及效果有一定提高.

表2 聚類結果評價

3 結語

本文提出了一種基于自調節步長果蠅優化的自適應密度峰值聚類算法(SCFO-DPC).SCFO-DPC算法通過可自調節步長的果蠅優化算法得到最佳截止距離,解決了需要根據人工設置截止距離參數的問題,并且得到的參數優于其他優化算法;能夠自適應的選擇聚類中心,有效的解決了人工選擇聚類中心為聚類算法帶來的不穩定性.通過測試,SCFO-DPC算法在對人工數據集、UCI 真實數據集的處理上具有相當大的優越性,比FODPC、DPC、DBSCAN 和K-Means算法更準確有效,且受人為影響更少.