庫區邊坡地震-滲流耦合數值模擬

蔣曉君，周柯軍，葛萬明，楊 帆

(1.無錫市太湖閘站工程管理處，江蘇 無錫 214023，2.無錫市惠山區陽山鎮水利農機服務站，江蘇 無錫 214023，3.無錫市水利設計研究院有限公司，江蘇 無錫 214023，4.無錫市泓利工程監理有限公司，江蘇 無錫 214023 )

地震是危害邊坡穩定的關鍵性因素[1-3]，地震-庫水位共同作用下，壩體與壩基會產生超孔隙水壓力[4-5]，使得壩體與壩基的有效應力急劇減小，導致地面噴砂冒水、沉降不均勻、地基失效、滑坡等一系列災害[6-9]，因此，對庫區邊坡動力-滲流耦合下的邊坡力學相應的認知是正確把握地震災害機理及防治地震邊坡失穩的關鍵。

國內外學者對地震-滲流耦合下的邊坡穩定展開了一定的研究工作，主要集中于理論、試驗及數值模擬上，理論方面：楊長衛[10]等利用Hilbert-Huang變換，提出SV波作用下巖質邊坡地震穩定性的時頻分析方法；肖世國[11]等基于限分析上限定理，推導了黏土土坡永久位移的計算方法；高科[12]基于突變級數理論，對邊坡的地震穩定性進行了綜合評定。試驗方面：葉海林[13]采用大型振動臺，對邊坡動力破壞特征進行了室內試驗研究；張澤林[14]對黃土-泥巖邊坡動力相應進行了離心機試驗。數值模擬方面：范昊天[15]利用離散元軟件PFC對含軟弱夾層邊坡地震作用下的破壞規律進行了數值模擬；李源亮[16]建立了邊坡的節理有限元模型，對其不同參數進行了敏感性分析。但是以上研究多針對邊坡失穩最終形態或者邊坡某點的應力狀態進行分析，較少對地震-滲流耦合下的孔壓，位移及安全穩定評價進行全面分析。

本文基于某堤壩工程，利用巖土軟件Geostudio中的SEEP/W，SLOPE/W及QUAKE/W模塊，實現了堤壩滲流-地震耦合計算，重點研究了地震作用下的浸潤線，超孔壓，特征點位移，永久位移及動力穩定性，研究成果為全面認識堤壩滲流-地震動力穩定性規律提供了一定的參考。

1 計算理論

1.1 非飽和滲流原理

非飽和滲流微分方程可以表達成為公式(1)：

(1)

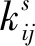
1.2 地震動力分析方法

動力作用下土體趨向軟化，因此，可以利用G/Gmax來刻畫等效線性模型中的現象如公式(2)～(4)：

(2)

K(γ，PI)=

(3)

(4)

其中，G為地震作用下的土體瞬時剪切模量，Gmax為0應變時的剪切模量，γ為土體容重，PI為塑性指數，n(PI)為和塑性指數有關的函數。

地震中的動水壓力是周期N的函數，NL是特定土體在特定地震條件下造成液化所需施加的應力周期數，孔隙水壓力比γu與N/NL有關，如公式(5)所示：

(5)

其中，孔壓可以表達成為公式(6)：

μ=γu×δ(static)

(6)

式中：μ為動孔隙水壓力，γu是孔隙水壓力比，δ(static)是有效靜態圍壓。

1.3 地震-滲流耦合下的動力穩定計算理論

根據抗滑穩定的定義，邊坡的動力安全系數可以表達成為公式(7)：

K=

(7)

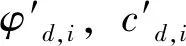
2 計算模型及邊界條件

2.1 計算模型

計算模型選擇某水庫堤壩，壩高44 m，壩基厚度取為10 m，壩基寬度為350 m，壩頂寬為16 m。該堤壩壩殼料為黏質砂，壩內為中密砂，而壩基材料則為花崗巖。該堤壩的正常蓄水位為33 m，下游設置排水。一共設置18個監測點來監測壩體內部的孔隙水壓力、位移變化規律，分別標號為1#～18#，相應位置見圖1紅點標注。整個模型一共劃分為1612個節點，1689個單元。

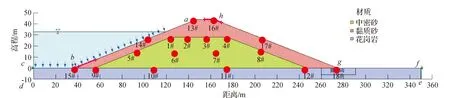
圖1 計算模型及模型網格

2.2 邊界條件

對模型進行滲流應力分析需要知道滲流及應力初始條件，滲流初始條件為邊界abcd33 m水頭計算所得的穩定滲流場作為整個模型滲流計算的初始條件，應力初始條件則是cd、fe固定x向位移，de固定xy向位移下的地應力平衡結果作為整個工況下的初始應力場。

邊界條件設置如下，滲流邊界為：abc為33 m定水頭邊界，gf為排水邊界，其余邊界為不透水邊界。進行地震動力計算邊界為：de為固定xy向位移邊界，cd，fe則為固定y向邊界。

3 計算參數設置

不同材料的非飽和滲流參數根據VG模型進行估算，材料物理力學參數如表1所示，滲透系數函數及體積含水率函數如圖2所示。土體的動力參數采用非線性模型，動力特性如圖3所示。地震波的時程曲線見圖4。

表1 材料物理力學參數

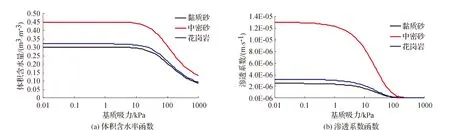
圖2 土-水特征曲線函數

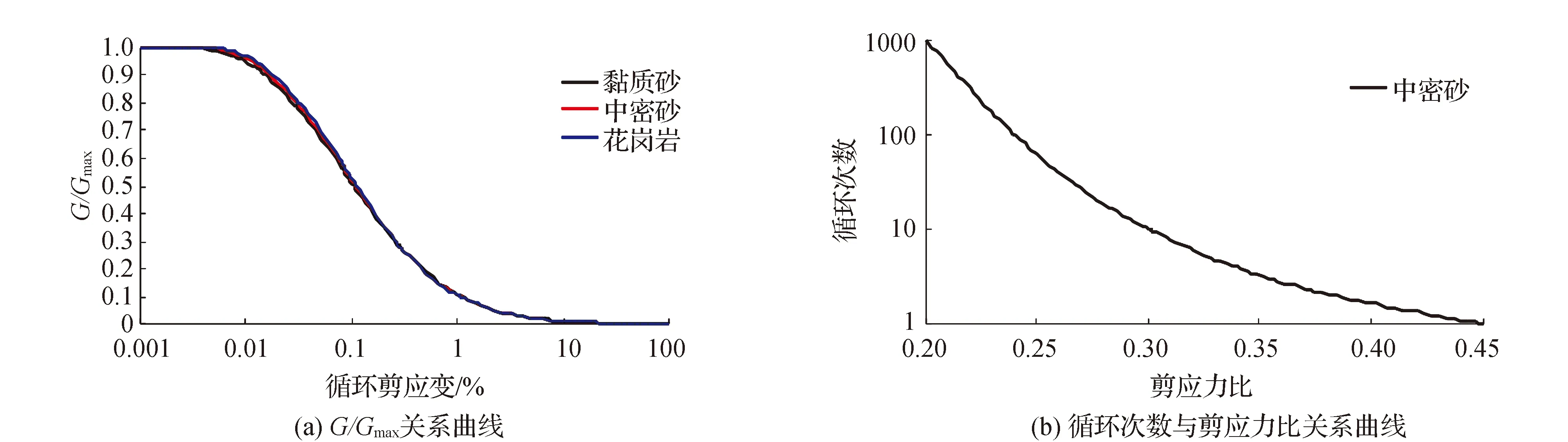
圖3 土體動力特性曲線

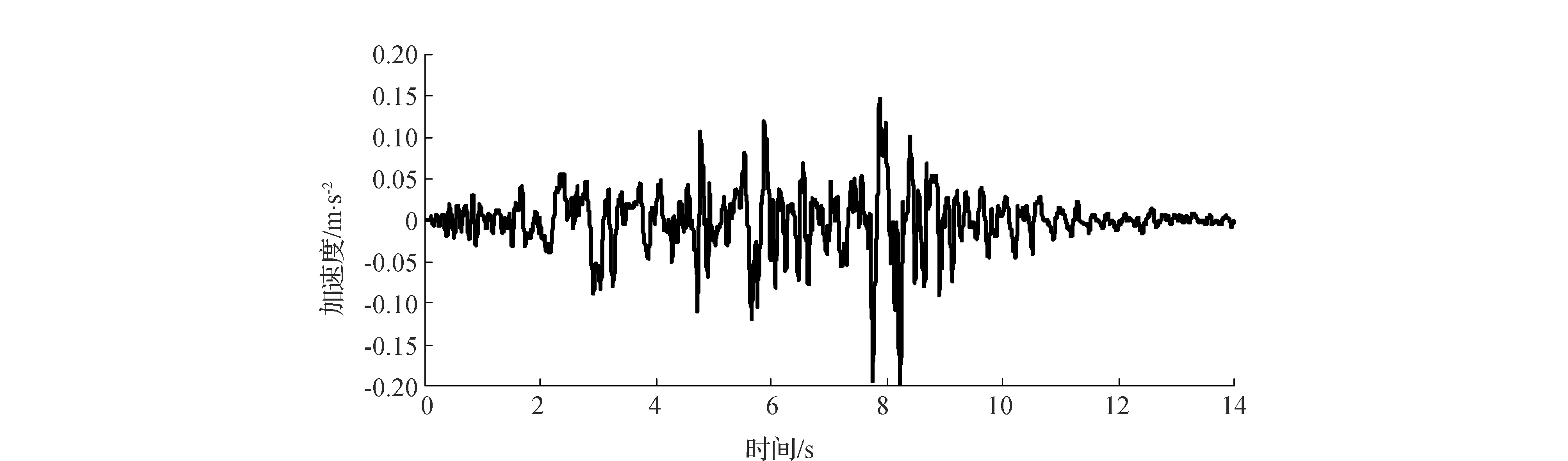
圖4 地震加速度時程曲線

4 結果分析

4.1 動孔壓分析

圖5為監測點1#～12#的超孔隙水壓力隨時間的變化規律。其中監測點1#～4#代表中密砂的上部，監測點5#～8#代表中密砂的中部，而監測點9#～12#代表中密砂的下部。

圖5 中密砂不同監測點的超孔壓變化規律

由圖可見：隨著地震的持續，堤壩內部超孔壓呈現不斷上升的趨勢。對于中密砂上部監測點，不同監測點(1#、2#、3#、4#)的超孔壓的增量分別為80.1 kPa，55.6 kPa，10.2 kPa及29.8 kPa，可見對于上部監測點而言，監測點越靠近上游，超孔隙水壓力的數值越大。

對于中密砂中部監測點而言，當監測點位于上游側(監測點5#、6#及7#)，超孔壓增幅不大，分別為38.2 kPa，19.2 kPa及61.1 kPa，而位于下游側的監測點8#孔壓增幅最大為128.1 kPa，且位于下游側的監測點在地震未結束時超孔壓便已經達到最大并在隨后的地震過程中保持不變。

對于中密砂下部監測點，超孔壓的增幅明顯低于上部與中部。位于上游側的監測點9#超孔壓增幅最大，為38.8 kPa，而其他監測點(10#、11#、12#)的超孔壓增幅最小，分別為16.1 kPa、3.7 kPa和17.0 kPa。

4.2 位移量分析

選取如圖1所示的13#～16#測點進行位移監測，堤壩在地震作用下的位移變化規律如圖6所示。

由圖可見：對于上下游測點而言，監測點高程越高，水平向的位移變化幅度越大，位于壩體上部的監測點13#和14#的水平向位移在地震過程中的變化比底部監測點大，在3.3 s達到最大值，約為12 cm。壩頂處的水平位移最大，上游壩腳處的水平位移最小。但是上下游測點的水平位移變幅差別不大。

堤壩上游側豎向位移變幅要大于下游側，但是豎向位移的變幅要遠小于水平位移變幅。頂監測點13#的最大豎向位移為0.06 m，出現在8.6 s；14#為0.0304 m，出現在9.1 s；15#為0.0056 m，出現在8.3 s。輸入加速度的最大值出現在8.22 s，可知壩體最大豎向位移滯后于輸入加速度最大值。豎向位移隨時間的變化曲線與輸入加速度較為接近，但是有滯后效應。下游側土體豎向位移變化規律與上游側相似，豎向位移最大值都是壩頂>壩中>壩腳，但是最大值小于上游側；壩頂、壩中和壩腳最大值分別為0.037 m、0.035 m和0.015 m。

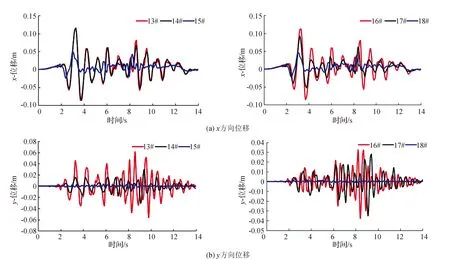
圖6 堤壩上下游不同測點的位移變化規律

4.3 安全系數變化規律

地震作用下的上下游壩坡的安全系數變化規律如圖7所示。

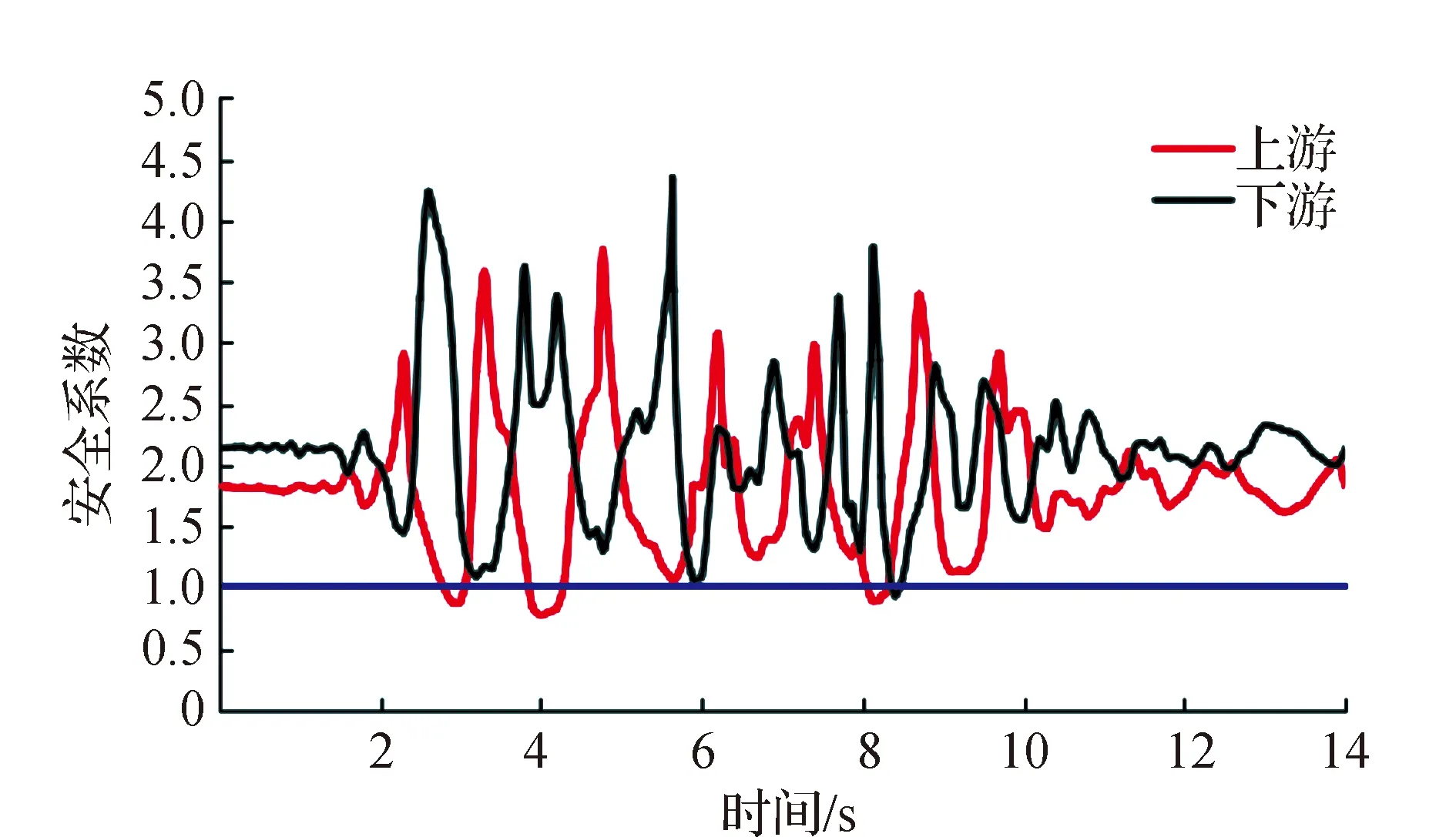
圖7 堤壩動力安全穩定及永久位移

由圖可見：上下游壩坡在地震過程中均出現小于1的情況，但是上游壩坡最小安全系數為0.82，要小于下游壩坡的0.91，表明在地震過程中上游壩坡更容易失穩，結合動壓力與后移量分析可知，地震過程中的上游側的超孔壓較高，有效應力較低，容易發生液化失穩，因此上游側的安全系數較低。

5 結 論

(1)地震作用下堤壩內部浸潤線具有一定變化，主要升高部位在于中密砂內部，而在黏質砂部位浸潤線的變化幅度則不大。

(2)堤壩內部中密砂上部及中部的有效應力變化劇烈，下部變化幅度較小，且臨近上游側的上部地震過程中發生液化失穩。

(3)上下游壩坡在地震過程中均出現小于1的情況，上游壩坡最小安全系數為0.82，下游壩坡最小安全系數為0.91，表明地震過程中上游壩坡更容易失穩。