含分布式電源配電網絡重構遺傳算法優化研究

賈文宇

（華北水利水電大學，河南 鄭州 450045）

0 引 言

配電網重構是一種基于系統運行狀態，經優化網絡拓撲來提高網架運行效率與電能質量的舉措。現階段，學者在研究配電網優化問題上大多采用數學優化理論算法[1]。其中GA具有簡單、便捷、收斂性佳以及全局搜索能力強等優點而被廣泛應用于配電網重構問題的求解中[2]。但是常規的GA無法針對配電網的結構特性進行編碼和遺傳操作，這在一定程度上會產生大量不可行解，進而弱化搜索效率。此次研究針對上述問題提出一種應用于含分布式電源配電網重構的GA優化方式，在優化GA編碼方式的基礎上，將機會約束檢驗融入到生成種群和交叉變異等流程中，以此求解含不確定性的配電網重構問題，進而為運行工作者的調度決策提供借鑒。

1 含不確定性的配電網重構模型

1.1 最大供電能力的機會約束模型

配電網最大供電能力指標即配網在達到節點電勢差約束與支路容量約束條件下所輸出的最大負荷[3]。目標函數如下：

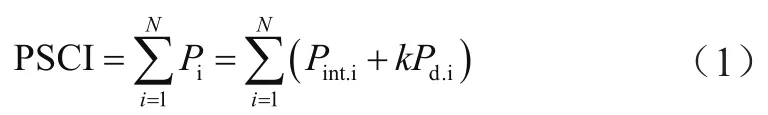
式中，N代表節點個數；Pi代表各節點最大負荷；Pint.i代表節點i的同步負荷；Pd.i代表節點i的負荷增長基數；k為負荷增長系數。為了客觀的對比優化結果，將最大供電能力等效為最大供電倍數K，進一步定義K=1+k[4]。

供電能力計算的約束條件如下：

式中，Uimin、Ui以及Uimax分別代表節點i的電勢差、下限以及上限；I1和I1max分別代表l流過的電流及其上限；f(Ps)和f(Pw)分別代表光伏和風電的出力概率密度函數；Ps、Psmax、Pw以及Pwmax分別為抽樣得到的光伏、風電輸出功率及上限[5]。

此次研究采用重復潮流法計算供電能力，在潮流計算的過程中，將分布式電源等效為PQ節點，在此基礎上經正態分布體現節點負荷的不確定性。含分布式電源與負荷等不確定因素，所得供電能力機會約束模型為：

式中，Pr即分布式電源等效特定節點負荷；K為不確定信息下的最大供電倍數；Kmargin表示供電能力安全閾值；α為預設供電能力機會約束置信水平。

1.2 含供電能力和分布式電源出力機會約束的配電網重構模型

將統計模擬得到的最大供電倍數K基于降序進行排列，依附于預設的置信水平可以獲得供電能力安全閾值Kmargin，以此數值最優為重構目標，構建的目標函數為 max。

在重構的過程中，一定要達到下述約束條件：

式中，Pr為支路供電能力安全閾值；Pi和Uj分別表示不確定狀態下支路i的功率和節點j的電勢差；Pimax和Ujmax分別表示支路i允許功率極值與節點j允許電勢差極值；α、β1以及β2分別表示供電能力、支路容量以及節點電勢差的置信水平；N1和N2分別表示網架支路和節點總量；g即各重構完成的配電網架結構；Qi為各網架支路節點功率；G為各輻射狀連通網架集合。

2 GA優化及其應用流程

因為配電網具有閉環設計和開環運行的特性，所以在重構時要從根本上確保所有個體的輻射和連通性。因此，在應用于配電網重構領域時要對GA實施進行下述優化[6]。

2.1 初始種群生成策略

針對常規問題，一般的編碼方法大多是通過二進制數對全部開關進行編碼，也就是通過0和1去體現聯絡開關和分段開關的開合狀態，此方案的特點是編碼便捷和容易操作[7,8]。不過此方法并未考慮配電網的運行特點，會造成算法運行時產生大量不可行解，更有甚者會直接影響計算效率[9]。此次研究的編碼方法中，針對某個含b個節點和l條支路的配電網架，將組成符合網絡拓撲約束網架的各支路編號整合到集合N1，將其他支路編號整合到集合N2，連結N1和N2即可形成新個體。經這種將網架樹枝和連枝分別編碼的方法，能夠確保初始種群內的所有個體都具備輻射性與連通性，因此確保算法求解的可行性要求。生成流程如下：

（1）設置N為所有備選線路集合，N1和N2即空集合，D表示網架變壓器所在節點集合；

（2）從N中找出全部帶有D中節點的支路，在此基礎上隨機抽取一條作為新增線路；

（3）將流程（2）抽取的支路整合到N1之中，如果N1線路組成的網架無法達到輻射性要求，那么將此支路整合到N2，反之將此支路的末節點加入D；

（4）重復流程（2）和（3），在N線路已全部加入N1和N2后停止，對新個體實施各項機會約束檢驗，如果達到標準即可加入初始種群，反之回到流程（1）；

（5）在初始種群中個體數量達到預設值的情況下算法結束。

2.2 交叉操作流程

為了從根本上確保初始種群中的個體在交叉操作后仍達到拓撲約束要求，對交叉操作算法實施下述優化。（1）從初始種群內以輪盤賭形式選擇兩條染色體作為父、母代；（2）在特定長度區間中隨機選擇一個染色體交叉點，將處于父代交叉點前的全部支路編號加入子代染色體的集合N1；（3）刪除母代染色體內所有和子代染色體相同的支路編號；（4）將母代染色體內其它支路編號逐一整合到子代染色體，每次整合都要對“環”進行檢查，如果達到輻射性要求即可加入集合N1，反之加入N2；（5）對構造的子代染色體實施各項機會約束檢驗，如果達到約束要求，則交叉操作完成，反之回到流程（1）。在進行交叉算法時，首先選取父代部分輻射狀支路加入到子代染色體，在此基礎上從母代內選取不重復的支路逐一加入到子代染色體。通過上述方式所形成的子代個體內包含了父母代的信息，而且拓撲結構達到連通輻射性要求。

2.3 隨機機會約束檢驗方法

在進行遺傳操作時，要對算法中的個體實施電勢差、功率以及供電能力機會約束檢驗[10]。此次研究采用統計模擬檢驗機會約束條件，流程如下。（1）已明確置信水平α，對于初始種群和重構時所生成的某個個體，設ξ=(ξ1,ξ2,ξ3,…ξn)為n維的隨機向量，ξ1,ξ2,ξ3,…ξn分別表示分布式電源和各節點負荷所滿足的概率分布；（2）從n維隨機向量ξ內隨機生成一組抽樣值θ1,θ2,θ3,…θn，也就是分布式電源出力和各節點負荷的一組單次計算抽樣值；（3）對此時的個體實施確定性潮流計算，進一步檢查電勢差、功率有無越限，通過重復潮流法計算此狀態下最大供電能力倍數K，如果K≥Kmargin，同時各節點電勢差和支路功率不越限，即可明確事件成立；（4）擬定試驗次數為S，S′即所有試驗次數中事件成立的次數，如果S′/S＞α，即可認為達到置信水平α，隨機機會約束條件成立，此個體為可行解。

2.4 算法流程

GA優化整體流程如下。（1）選擇GA初始參數，其中包括種群大小以及變異概率等；（2）生成滿足連通輻射性的網架加入種群；（3）依附于光伏電池、風機以及負荷的概率密度函數實施統計模擬，在此基礎上對種群中染色體進行機會約束檢驗，如果未達到標準則重新生成并替換；（4）將統計模擬得到的供電能力結果根據降序進行排列，依附于置信水平獲取染色體適應值；（5）通過輪盤賭的方式選擇兩條父代染色體，對父代染色體實施交叉操作生成一條子代染色體，此染色體同樣達到拓撲約束要求，在此基礎上依附于設定的變異概率對此染色體實施變異操作；（6）和流程（3）相似，對子代實施機會約束檢驗，同時計算子代適應系數，如果沒有達到機會約束或適應系數較之原種群沒有提高，則返回流程（5）；反之將子代加入種群替換適應系數較低的染色體；（7）在種群中全部染色體都相同的情況下，即可證實算法已收斂。

3 算例分析

筆者通過IEEE-33節點配電網系統進行驗證。IEEE-33節點網架拓撲結構見圖1。初始網架的整體負荷為3 715 kW+j2 300 kvar。在節點8與24分別接入光伏發電系統與風力發電系統，風機切入風速為4 m/s，額定風速為12 m/s，切出風速為25 m/s，額定功率為400 kW。光伏系統整體面積為10 000 m2，光電轉換效率為0.14。

圖1 初始網架拓撲

3.1 含分布式電源的配電網重構結果分析

在通過GA求解模型的情況下，初始種群大小擬定為20，變異率擬定為0.1，統計模擬次數N為5 000。取各約束條件的置信水平為0.8，設置不同的分布式電源，得到的重構結果如表1所示。

表1 網絡重構結果

通過表1能夠得到以下結論。在重構方案中，無分布式電源方案供電能力增加6.05%，而接入光伏系統和風機的方案供電能力分別增加7.25%與5.15%，由此可證，在重構的過程中加入供電能力機會約束能夠在一定程度上深化配電網供電能力，同時接入分布式電源對供電能力的改善更為顯著。在不同類型分布式電源同時接入配電網的情況下，供電能力達到最優，由此可證，采用此次研究所提出的重構方法對含多種分布式電源的配電網實施重構，能夠在一定程度上增加網絡的供電裕度，同時可以加強配電網的利用率以及安全性。

3.2 置信水平對優化方案影響分析

在光伏系統和風機同時接入的情況下，分別取不同的置信水平對模型實施求解，重構結果如表2所示，其中置信水平為0.8狀態下的收斂曲線如圖2所示。

表2 網絡重構結果

圖2 置信水平為0.8的收斂曲線

通過表2的重構結果，得到以下結論。（1）在配電網同步接入多種分布式電源的情況下，重構結果的供電能力會隨著約束條件置信水平的提高而降低，由此印證對機會約束要求越高，方案的供電能力就越低。（2）低置信水平下的重構結果盡管具有較高的供電能力，但無法體現全局狀態，且出現極端狀況的概率較高，實際應用性偏低。而提高置信水平導致供電能力降低，對重構結果的安全性會產生影響，所以置信水平不宜過高。（3）總的來說，在多種分布式電源同步運行的狀態下，可選擇置信水平0.8作為參考數值，此時重構結果兼顧了置信水平和供電能力的要求，具有較強的適用性。

4 結 論

此次研究融合了機會約束理論，構建含供電能力機會約束的配電網重構模型，分析了配電網負荷和分布式電源出力的不確定性，從根本上避免了確定性負荷下重構結果過于保守的問題，優化方案更為豐富，且具有更高的適應性。此外，此次研究GA優化可以依附于配電網運行特性，規避不可行解，深化算法效率，在此基礎上明確負荷和分布式電源出力的隨機性，加強了方案對不確定性的適應度。算例結果表明此次優化算法的有效性，進一步印證了它適用于不確定性配電網重構問題。算例結果顯示，經筆者所提方法實施重構，能夠從根本上加強配電網供電能力。在配電網同步接入多種分布式電源的情況下，置信水平越高，優化方案的供電能力就會隨之降低，所以要依附于實際運行需求進行有針對性的設定與調整。