固定翼無人機電磁彈射用直線感應電機設計與研究*

劉希軍 朱新宇 高麗霞 劉小涵

中國民用航空飛行學院 航空工程學院，四川 廣漢 618307

目前，固定翼無人機起飛方式主要有火箭助推起飛、軌道彈射起飛、地面滑跑起飛、空中投放起飛、車載發射起飛、垂直起飛和手拋起飛等。較為常見的方式為火箭助推和氣液壓彈射技術。火箭助推方式在無人機起飛過程中，釋放大量的化學染料、煙塵和火光，成本較高，安全性能較低。氣液壓彈射技術經濟適用性較好，但其結構管路復雜，占地面積大，設備維護復雜性高[1]。

隨著電磁加速技術研究的不斷提升，越來越多的研究傾向于采用電磁彈射驅動固定翼無人機加速起飛。電磁彈射驅動效率高，精度高，加速均勻，維護方便[2]。相較于其他助推驅動而言，電磁驅動裝置不存在無效載荷，動力源成本低，耗能更少，噪音更小，且不會對環境造成污染。

針對無人機電磁彈射研究主要有線圈彈射和直線電機2種方式，相較而言，采用直線感應電機作為電磁驅動裝置，可通過改變設計參量改變電磁推力輸出，推力輸出更大更平穩，精度高，可控性強，設備更易于維護。通過對無人機起飛運動學分析，優化設計無人機起飛用長初級直線電機，驗證固定翼無人機彈射起飛的可行性。

1 無人機起飛運動學分析

采用電磁加速系統在預定的長度距離內，將固定翼無人機瞬間加速，并使其速度值達到無人機起飛規定標準。無人機發射簡化受力模型如圖1所示。

圖1 無人機發射簡化受力模型

假定被加速的輕型固定翼無人機及其載荷質量不超過40kg，彈射軌道長度5m，無人機要在0.36s內從0km/h加速到100km/h，加速過程中無人機自身動力系統不做功，直線感應電機提供恒定的電磁推力輸出，用于無人機的加速起飛牽引動力。

由牛頓第二定律對運動學過程表示為

(1)

(2)

(3)

式中，vt、Ls和t分別為固定翼無人機加速末速度、軌道長度以及加速時間；F、M和a分別為無人機沿軌道方向受到合力、無人機及動子滑塊總質量以及無人機的加速度。

其中，無人機沿軌道彈射方向合力為

F=Fem-(Ff+Gsin(θ))

(4)

Fem為直線電機產生的電磁推力；Ff為無人機彈射過程中受到的阻力；G為無人機及動子滑塊總重量；θ為發射角度，發射角度小于60°可調。

固定翼無人機在起飛彈射加速過程中，由于前部空氣被壓縮，機身兩側面空氣摩擦，以及尾部空間部分真空等因素，導致加速了過程空氣阻力。

無人機所受空氣阻力大小與其速度平方成正比，速度越大，所受空氣阻力越大。無人機所受空氣阻力為：

(5)

式中，C為阻力系數，其值的大小主要和運動物體的形狀、光滑程度以及迎風面物體的面積有關，無人機的風阻系數約為0.2～0.4；ρ為空氣密度，干燥空氣密度為1.293g/l；S0為物體迎風面的面積；v為物體與空氣的相對運動速度。

以固定翼無人機及其載荷質量40kg、發射角30°計算，所受空氣阻力相對于電磁推力較小，暫且忽略，欲使無人機在5m內加速到100km/h，則直線感應電機至少提供3.09kN的電磁推力。固定翼無人機加速過程具體指標如表1所示。

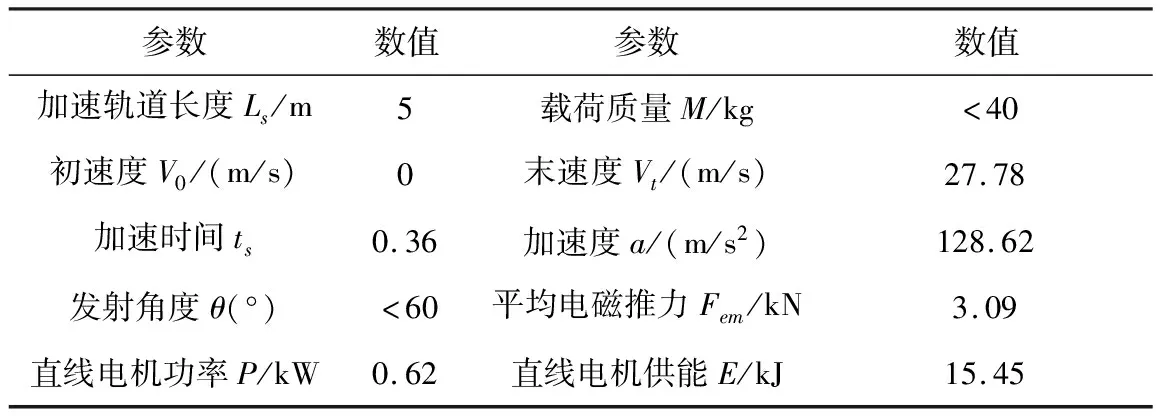
表1 無人機加速主要技術指標

2 直線感應電機數學模型建立

固定翼無人機起飛驅動用直線電機采用長初級無槽直線感應電機，其結構圖如圖2所示。電機的定子采用無齒槽的結構，這種方式可以增大定子繞組截面積，并減小磁場的齒諧波影響[3]。次級為鋁板或銅板，減小質量，降低制造和運行成本，且有利于進行高速大推力運動。

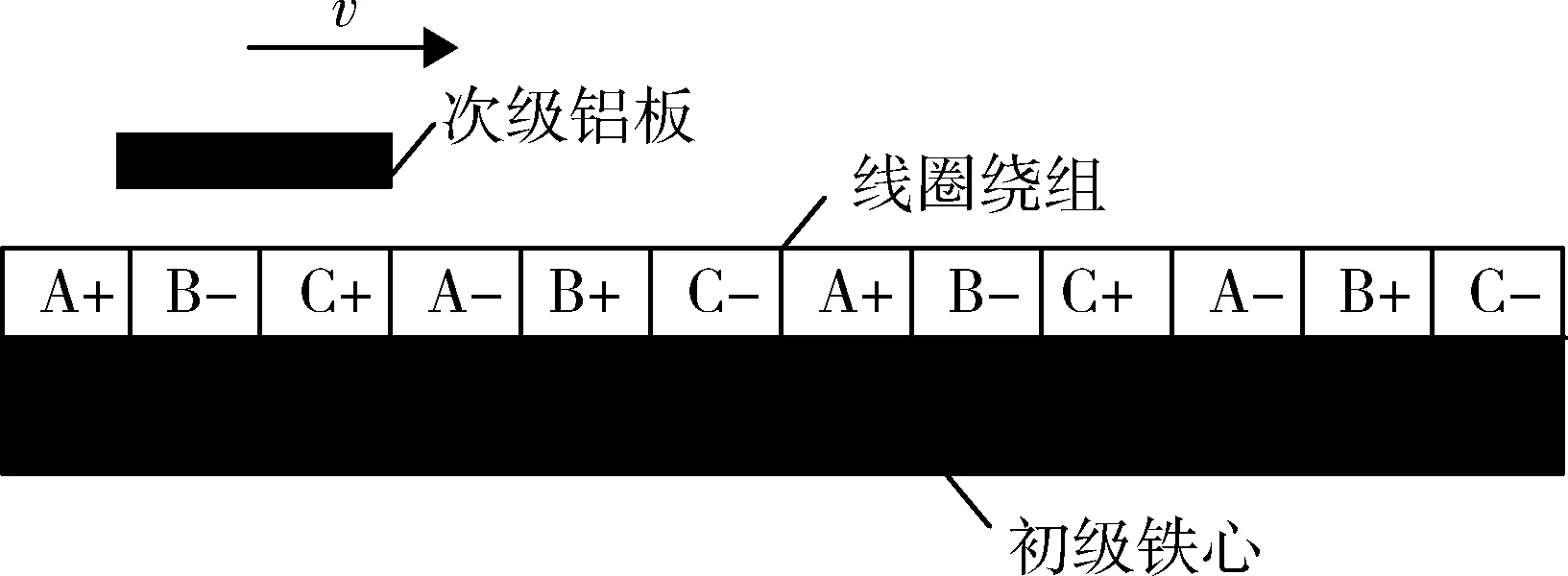
圖2 無槽直線感應電機結構圖

由于直線感應電機初級鐵心及繞組兩端開斷，這種特殊結構使得直線電機中存在邊端效應問題，影響氣隙磁場，衰減推力輸出，邊端效應對電磁推力的輸出影響不可忽略。在無人機加速過程中，可采用控制直線感應電機的定子的電流及滑差頻率，從而完成電機電磁推力輸出的優化控制。

考慮邊端效應對長初級無槽直線感應電機的影響，建立直線感應電機T型等效電路，推導電機電磁推力輸出表達式，通過等效電路可以計算出直線感應電動機相關的機械特性。考慮邊端效應的長初級直線感應電動機的等效電路如圖3所示。

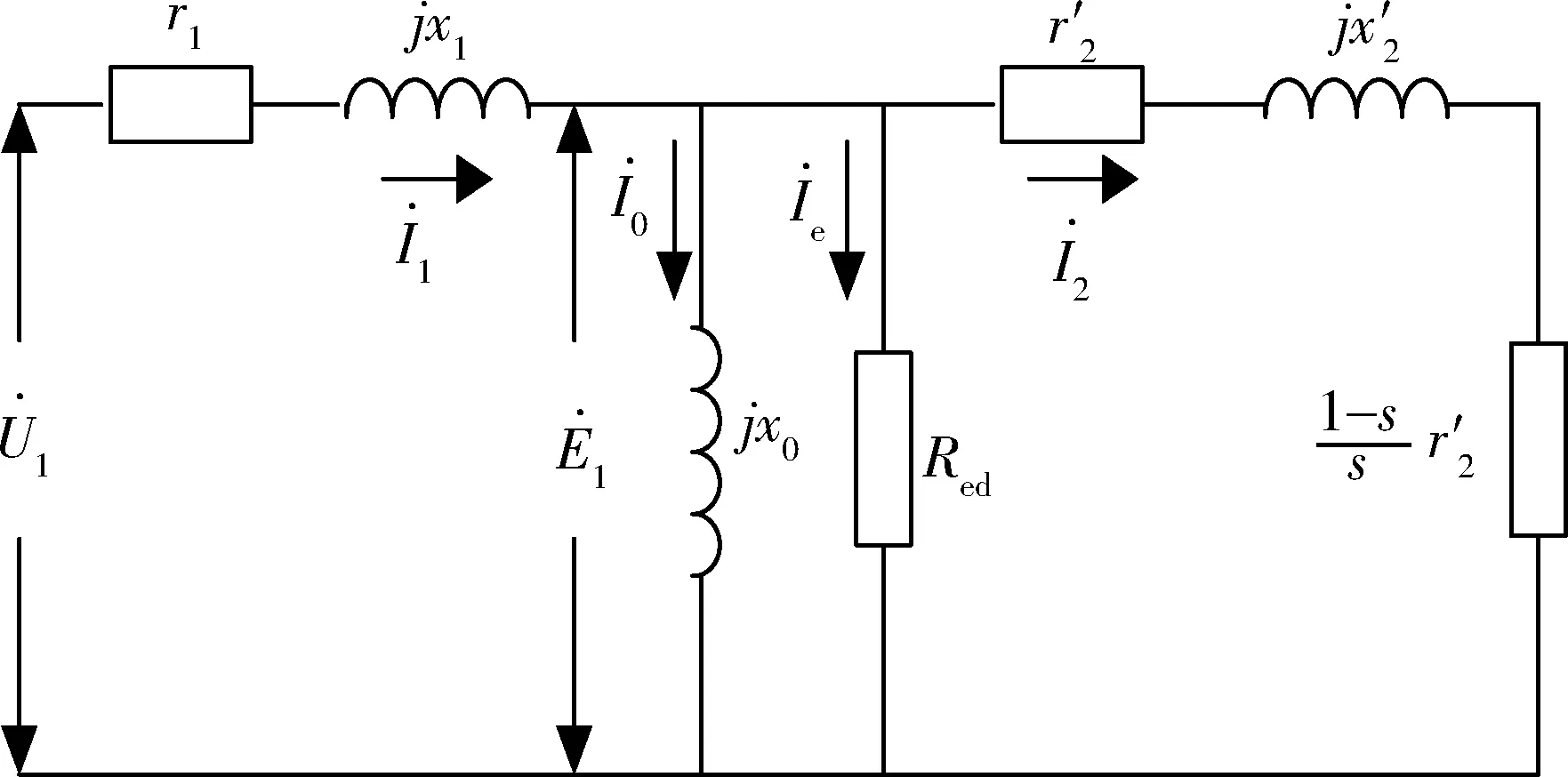
圖3 考慮邊端效應的直線電機等效電路圖

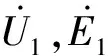
(6)

式中：

(7)

ρa為次級電阻率；la為次級導體寬度；ω1為初級相串聯匝數；p為直線電機極對數；da為次級導體厚度；τ為直線電機極距。當電機結構參數確定后，邊端效應等效電阻Red僅與滑差率s相關。

3 直線感應電機推力分析

采用基爾霍夫定律計算分析考慮邊端效應的無槽單邊直線感應電機等效電路。由基爾霍夫電壓定律可得：

(8)

(9)

(10)

由基爾霍夫電流定律可得：

(11)

根據考慮端部效應的直線感應電機等值電路和基爾霍夫定律，推導無人機起飛驅動用直線電機電磁推力輸出：

(12)

(13)

整理式(12)和(13)可得電磁推力輸出：

(14)

額定頻率f1，滑差頻率fs與滑差率s存在關系：

fs=s·f1

(15)

因而可通過控制滑差頻率，改變所需電機的動力輸出。

在驅動過程中，通過控制滑差頻率控制直線感應電機的電磁推力輸出，即保持電機初級繞組電流值恒定不變，亦可通過控制滑差頻率控制氣隙磁場及渦流場，進而實現電磁推力輸出的控制。

根據無人機加速運動學性能指標要求，設計彈射用直線感應電機尺寸，進而確定等效電路各參數值。

(16)

式中，kr1為電阻增長系數，取kr1=1；ρ為繞組導線電阻率；lav為初級繞組平均半匝長度；S1為初級繞組導線截面積。

忽略氣隙基波漏電抗，則初級繞組漏電抗x1為：

(17)

式中，lδ為電機初級鐵心疊厚；q1為電機每極每相槽數。

(18)

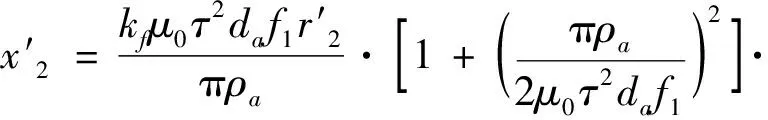
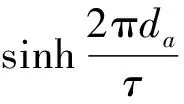
(19)

kdp為基波繞組系數[4-5]，kdp=1；da為次級鋁板厚度；kf為集膚效應系數[6]，忽略集膚效應，則kf=1。

勵磁電抗x0為:

(20)

式中，μ0=4π×10-7H/m為真空磁導率；δe為電磁氣隙。

4 直線電機參數設計及分析

根據固定翼無人機加速起飛設計指標要求，設計一款加速驅動用無槽型單邊直線電機，用于提供無人機在起飛階段的電磁推力輸出。設計加速驅動電機部分尺寸參量如表2所示。

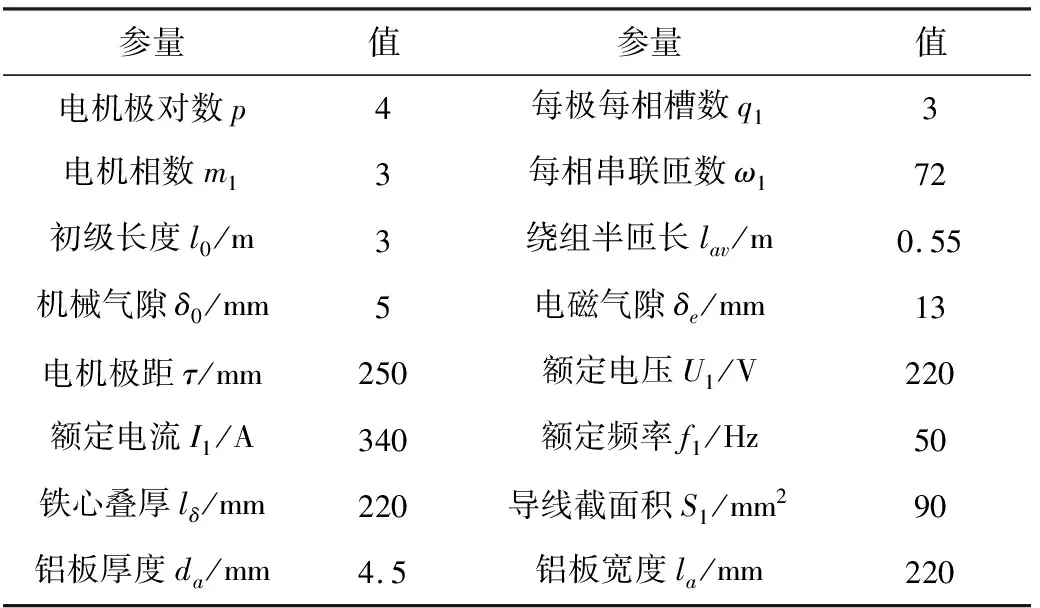
表2 無槽單邊直線感應電機設計部分參量

電機極距的變化將影響電機電磁推力的輸出。增大極距有利于增大基本行波推力，但極距的增大會造成端部漏抗和損耗的增加。同樣，直線電機極距不易過小，過小的極距不利于電磁推力的輸出，又會增大氣隙磁場基波漏抗。通常，加速用長初級直線感應電機極距的取值范圍為τ=0.2～0.5m。

適當增加電機極數有利于減小端部極所占總比重，進而減小縱向端部效應的影響。然而，當直線電機的長度和極距確定后，電機的極數必然受到制約。通常，直線電機極數取值為p=4～8。

傳統型直線電機均采用齒槽結構，對于大功率電磁加速用長初級直線感應電機，無齒槽的設計方式，有利于增大定子繞組截面積，亦可以有效的消除氣隙磁場齒諧波[7-9]，每極每相槽數取值為q1=1。

電磁加速用大功率直線感應電機常采用單條式繞組，每相串聯的匝數與供電線電壓成正比，和供電頻率成反比。調整每相串聯匝數可以保證直線電機輸出被加速物體所需的電磁推力的輸出。

初級鐵心寬度的選取通常和直線感應電機的極距τ相關聯，初級鐵心寬度的取值范圍為la0=(1.5～3.5)τ。

為了減小橫向端部效應，直線電機次級寬度應略寬于初級鐵心寬度，橫向每邊伸出長度應大于τ/π，因而，次級導體的寬度選擇為la=la0+2τ/π。

根據直線電機次級導體板所承受的剪切應力和導體板寬度，確定次級導體的長度值[10]。

直線電機次級導體板的厚度選取同樣與電磁推力相關。厚度太小會減小行波推力輸出，而厚度過大時，端部效應越發明顯。加速用直線感應電機的次級板導體厚度通常選取為da=3～5mm。

懸浮氣隙值對直線感應電機電磁推力輸出影響明顯。無人機加速系統用直線電機的機械氣隙為5mm，電磁氣隙13mm，分析無人機運動速度20m/s時，電磁氣隙和直線電機推力的關系如圖4所示。

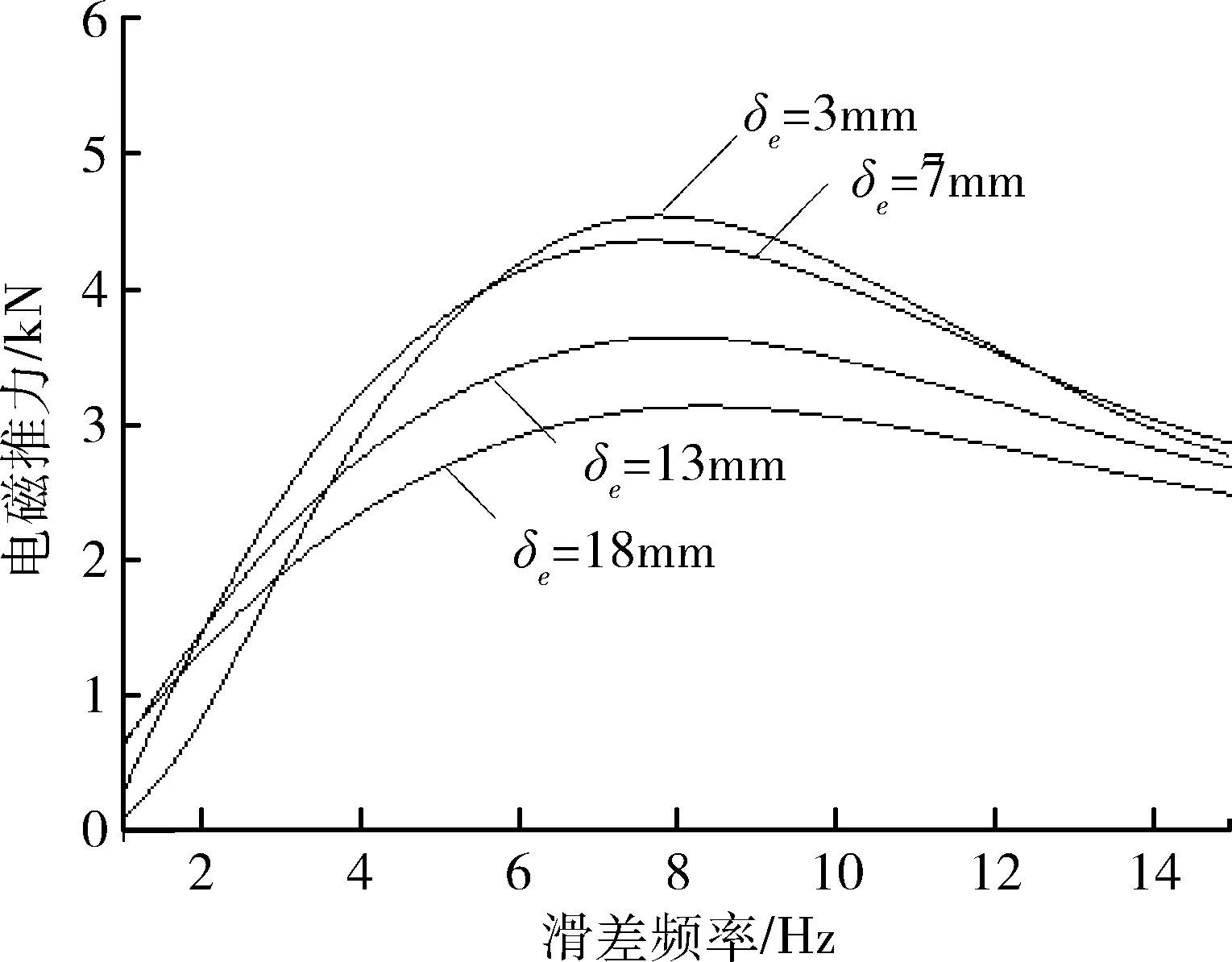
圖4 不同電磁氣隙下滑差頻率與電磁推力關系

通常，設計直線電機時應盡量減小氣隙長度，氣隙長度的大小與電磁推力輸出成反比。如圖所示，這種關系在滑差頻率大于7Hz時尤為明顯。

由于受到實際加工工藝的限制，以及熱膨脹的制約，電機氣隙長度不宜過小，氣隙長度過小會增加空間諧波磁場產生的附加損耗和脈振推力。

當滑差頻率大于14Hz時，不同氣隙下的推力輸出值趨于恒定且近似相近。

5 直線感應電機控制分析

固定翼無人機加速驅動用直線感應電機參數設計完畢后，對直線電機的控制方式進行仿真驗證。建立直線感應電機模型，仿真驗證理論分析計算的有效性。不同滑差頻率下，無人機加速過程中，運行速度與電磁推力輸出關系如圖5所示。

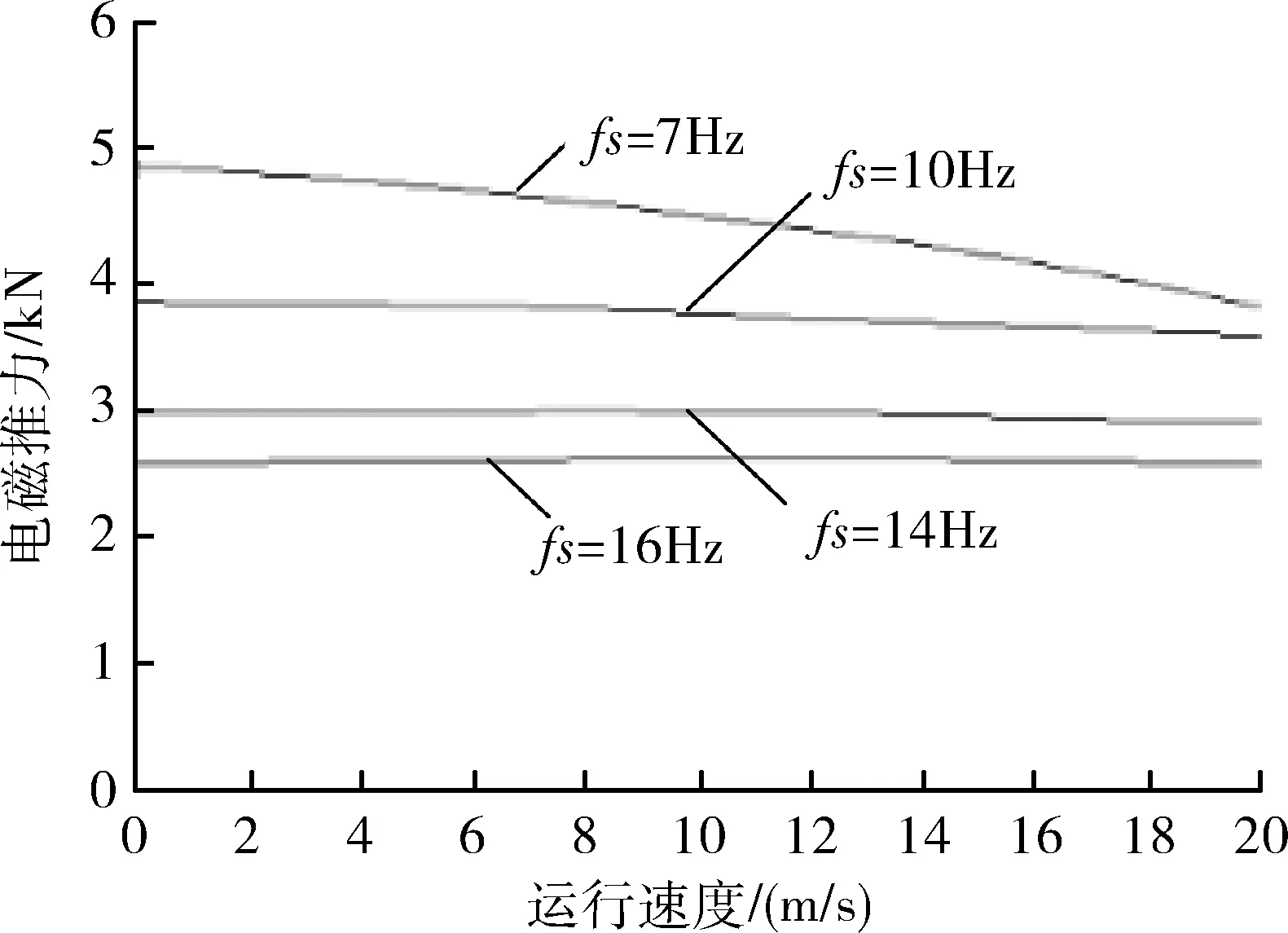
圖5 不同滑差頻率下運行速度與電磁推力關系

固定翼無人機起飛加速過程中，選取的滑差頻率越小，對應的電磁推力輸出越大。保持滑差頻率恒定，驅動用直線感應電機電磁力輸出隨無人機運行速度的增大基本保持不變，且滑差頻率取值14Hz左右時，電磁力輸出值受速度影響最小。

不同運行速度下，固定翼無人機加速過程中，滑差頻率和直線電機推力的輸出關系如圖6所示。

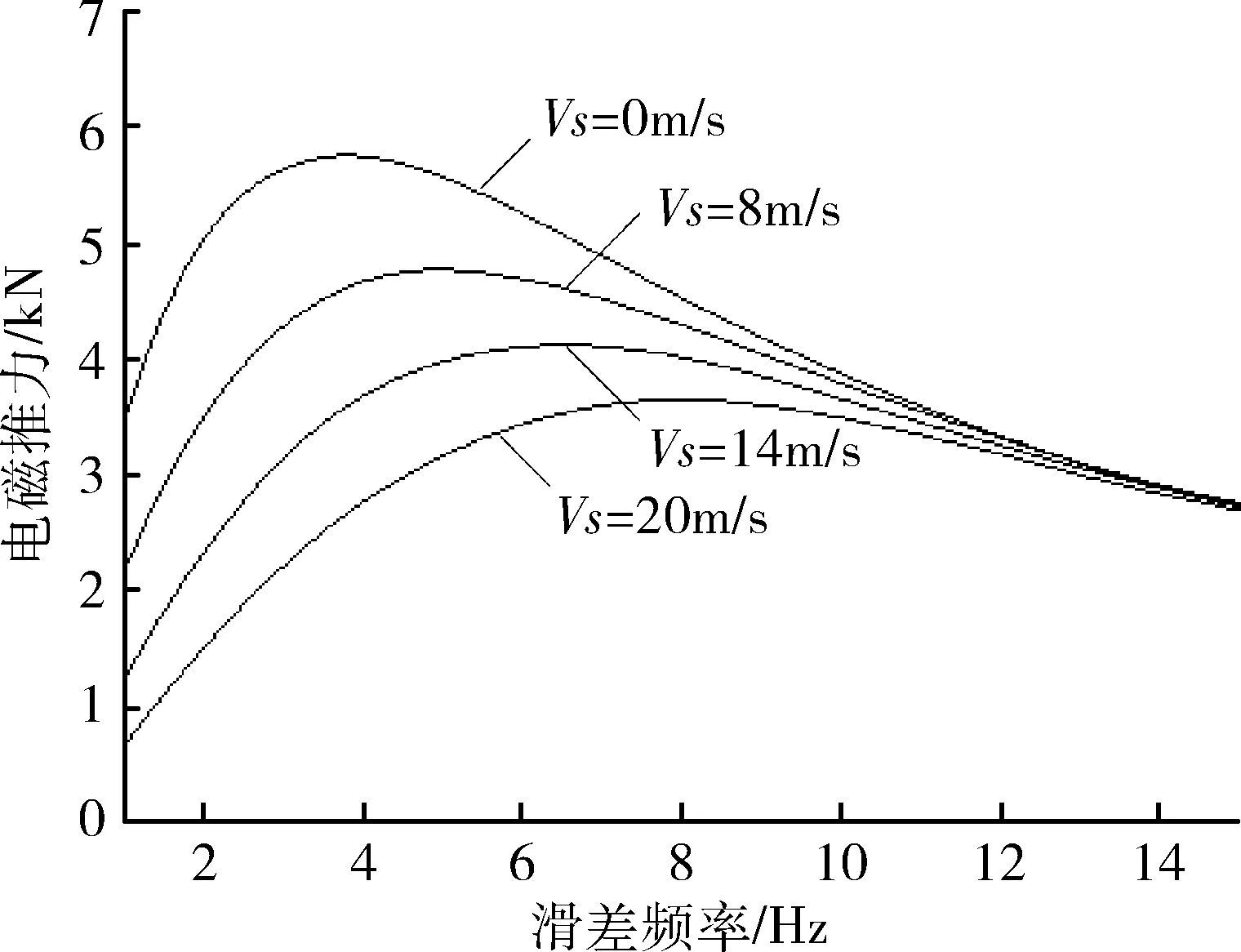
圖6 不同運行速度下滑差頻率與電磁推力關系

滑差頻率較低，速度不同，對應的電磁推力輸出亦不相同；滑差頻率較高，電磁推力輸出基本不隨速度的改變而改變。通過調節滑差頻率可以實現更大的電磁推力輸出，但同時過高的滑差頻率會增大驅動系統的功能損耗。磁懸浮列車用直線感應電機，滑差頻率取值13.69Hz時[11]，系統功耗最低。本加速系統采用滑差頻率取值14Hz完成固定翼無人機的加速彈射。

6 結論

隨著對固定翼無人機起飛加速要求的不斷提高，傳統型的起飛方式已經逐漸無法滿足無人機的起飛加速需求。本文研究了一種利用無槽式長初級直線感應電機作為驅動的電磁彈射加速方式。分析了無人機加速起飛的運動學過程，并根據起飛要求計算直線電機所需的電磁推力值，并以此為基礎設計一款用于加速系統用的直線感應電機，完成無人機的加速起飛。

直線感應電機的控制方式采用恒電流-滑差頻率控制，仿真分析不同滑差頻率對電磁推力輸出的影響，優化系統控制方式，減小驅動系統的功耗，完成固定翼無人機起飛需求。