分布式遺傳的船舶航向神經網絡優化控制

鄧華 王仁強 胡甚平 繆克銀 楊永前

摘要：針對海上風浪環境對船舶航行的干擾，利用遺傳神經網絡優化算法設計船舶航向控制器。利用分布式遺傳算法（distributed genetic algorithm，DGA）并結合模擬退火算法對常規遺傳算法（genetic algorithm，GA）進行改進。利用改進的GA對徑向基函數（radical basis function，RBF）神經網絡進行優化。利用優化的RBF神經網絡對系統不確定項進行逼近，并對控制輸入進行補償實現抗飽和控制。利用三階干擾觀測器對外部擾動實時跟蹤并反饋到滑模控制器（sliding mode controller，SMC）設計中。借助SMC設計并結合李雅普諾夫穩定性理論推算出船舶運動控制律，實現船舶運動優化控制。通過實驗驗證了本文設計的控制器性能較現有的模糊PID控制器和神經網絡SMC優越，系統達到穩定的時間短，平均超調量小。

關鍵詞： 船舶運動; 優化控制; 徑向基函數（RBF）神經網絡; 分布式遺傳算法（DGA）; 輸入飽和

Abstract： Aiming at the interference of the sea wind and wave environment on ship navigation， a ship course controller is designed by the genetic neural network optimization algorithm. The distributed genetic algorithm （DGA） and the simulated annealing algorithm are used to improve the conventional GA. The improved GA is used to optimize the radical basis function （RBF） neural network. The optimized RBF neural network is used to approximate the uncertain items of the system， and the control input is compensated to realize the anti-saturation control. The third-order disturbance observer is used to track the external disturbance in real time and feed it back to the design of the sliding mode controller （SMC）. With the help of the design of SMC and the Lyapunov stability theory， the ship motion control law is derived to realize the ship motion optimal control. Experiments show that the controller designed in this paper is of better performance than the existing fuzzy PID controller and the neural network SMC， the stability time of the system is shorter， and the average overshoot is smaller.

Key words： ship motion; optimal control; radical basis function（RBF） neural network; distributed genetic algorithm （DGA）; input saturation

0 引 言

航向跟蹤控制是船舶運動和控制領域的重要研究之一。它與船舶航行的經濟性和安全性[1-2]有關。目前，船舶航向控制以比例積分微分（proportional integral derivative，PID）控制[3]或自適應控制[4]為主，但這兩種控制均不能真正地解決海上風浪頻繁干擾問題和船舶非線性問題。具有模糊模型或自適應參數調整的改進型PID控制可以適應參數變化并減少控制抖動[5]。

一些新的控制理論方法不斷地應用于船舶航向控制，如李雅普諾夫穩定性理論和方法[6]、滑模控制[7]以及以模糊邏輯系統[5]和神經網絡[8-9]為代表的智能控制技術。

神經網絡系統[10]的最重要特征是具有自組織和自學習功能，并具有實時處理大規模并行信息的能力，因此可以有效地解決船舶運動模型的不確定性[4]。融合徑向基函數[8，10]（radical basis function，RBF）神經網絡的滑模控制器（sliding mode controller，SMC）可以有效地應用于具有不確定性的非線性系統（如船舶運動控制系統）的穩定、快速控制。值得注意的是，神經網絡用于運動系統的建模和控制的關鍵是確定神經網絡的結構和連接權重系數[10]。對于最典型的RBF神經網絡，連接權重和閾值等參數的設定主要取決于經驗，因此很容易陷入局部極值[10]。另外，設計控制器時還要考慮船舶控制輸入（轉向角輸入的飽和度）受限[11]和外部干擾兩個問題。

本文通過基于RBF神經網絡的內部輔助補償機制，引入抗飽和控制理論和技術，同時結合擴張觀測器克服外部干擾[12];利用分布式遺傳算法（distributed genetic algorithm，DGA）和模擬退火（simulated annealing，SA）算法對常規遺傳算法（genetic algorithm，GA）進行改進，將改進的GA和RBF神經網絡融入SMC中，設計出具有輸入飽和度的船舶運動抗干擾智能控制器。

1 基本方法

1.1 具有輸入飽和度的船舶運動模型

船舶運動模型有很多類型。常見模型包括整體模型、獨立模型和響應模型[13]。本文選擇響應模型來設計船舶運動控制器：

因此，本文的目的是在外部干擾、船舶模型存在非線性和不確定性及船舶系統輸入受限的情況下，設計一種智能化程度高的船舶運動控制器。

1.2 基于RBF神經網絡的抗飽和設計

采用抗飽和控制技術解決輸入受限的問題。為提高抗飽和性能，采用RBF神經網絡進行內部輔助補償[14]，見圖1。由圖1可知：船舶模型狀態變量的期望值為xd;控制器輸出為v;舵機伺服系統的抗飽和補償為u=v+δ;網絡輸出δ^為輸入飽和補償δ的估計值。

1.3 外部干擾觀測器

通過擴張觀測器[14]對外部干擾進行實時跟蹤估計，并反饋到SMC設計中，可以減少由外部干擾引起的控制抖動。三階干擾觀測器設計如下：

2 RBF神經網絡的優化

2.1 改進GA

RBF神經網絡應用前需要確定網絡參數，以保證網絡的高逼近性能，否則網絡很容易陷入局部極值問題[10]，從而導致控制抖動。本文將GA用于優化RBF神經網絡參數，將其有效地應用于船舶運動控制系統的設計中。

針對標準GA的不足，本文采用DGA。總種群分為幾個子群，每個子群獨立進行遺傳優化。各子群間定期將優良的個體按一定比例進行遷移，以確保各子群共享良好的基因模式，并防止某些子群向局部最優方向收斂。每個子群具有不同的基因模式，并且其遺傳過程具有相對獨立的進化空間，因此它們各自的進化方向是不同的，這確保了搜索的充分性和全局最優收斂結果。

2.1.1 基于SA算法的適應度修正

當使用經典輪盤賭方法選擇個體時，適應性較高的個體被連續選入下一代，而適應性較低的個體被丟棄，從而導致后代與前代之間的差異很小。在遺傳早期易產生早熟問題，而在遺傳后期易產生進化停滯現象。使用SA算法可以改善此問題。

在遺傳進化初期設定較高的溫度，此時具有相似適應性的個體產生后代的可能性也相似。在遺傳進化過程中，隨著溫度逐漸降低，先前相似個體之間的差異會被放大，從而使杰出個體的優勢明顯。

2.1.2 變異概率的改進

自適應變異概率可以根據遺傳進化同步更新。自適應變異方法可以用于在發生過早收斂時自動增加變異概率，從而擴大搜索空間。

2.2 基于改進GA的RBF神經網絡優化

將帶有SA算法的DGA用于確定RBF神經網絡的參數。RBF神經網絡的遺傳優化過程見圖2。將遺傳優化算法與RBF神經網絡計算融合在一起，可以實現閉環在線尋優，一次性完成尋優過程。

3 基于滑模控制的航向控制實現

將上述基于SA算法的DGA優化的RBF神經網絡應用于船舶運動智能控制設計。利用優化后的RBF神經網絡對船舶不確定項進行逼近，以及對控制輸入進行補償，實現抗飽和控制。進一步利用三階干擾觀測器對外部擾動實時跟蹤并反饋到SMC設計中。然后借助SMC設計并結合李雅普諾夫穩定性理論推算出船舶運動控制律，實現船舶運動智能控制。

利用滑模控制技術設計智能控制器，定義如下滑模函數：

4 實 驗

4.1 實驗條件與數據

以文獻[11]中的無人水面艇（unmanned surface vessel，USV）為例開展實驗。實驗中三階干擾觀測器的設計參數為：λ=0.05，k1=6，k2=11，k3=5。SMC設計參數為：c1=5，c2=15，η=0.1。網絡自適應參數為：γ1=15，γ2=15。GA進化總代數為150;子群數量為5;遺傳交叉算子為pc=0.85;變異算子參數pmh=0.5，pml=0.04;SA算法參數T0=100 ℃，Ta（t）=10 ℃。

4.2 性能驗證

在實驗過程中，當優化過程執行次數超過7時，優化過程趨于收斂。為便于數據計算，進行了奇數次實驗。圖3為截取的前9組實驗數據。與GA相比，DGA優化過程收斂更快，目標函數值更小。如表1所示：GA優化的目標函數的平均值為959.22，平均值與中位數的比值為1.006;DGA優化的目標函數的平均值為795（比GA的平均值小17.12%），平均值與中位數的比值為0.978（比GA的平均值小2.78%）。

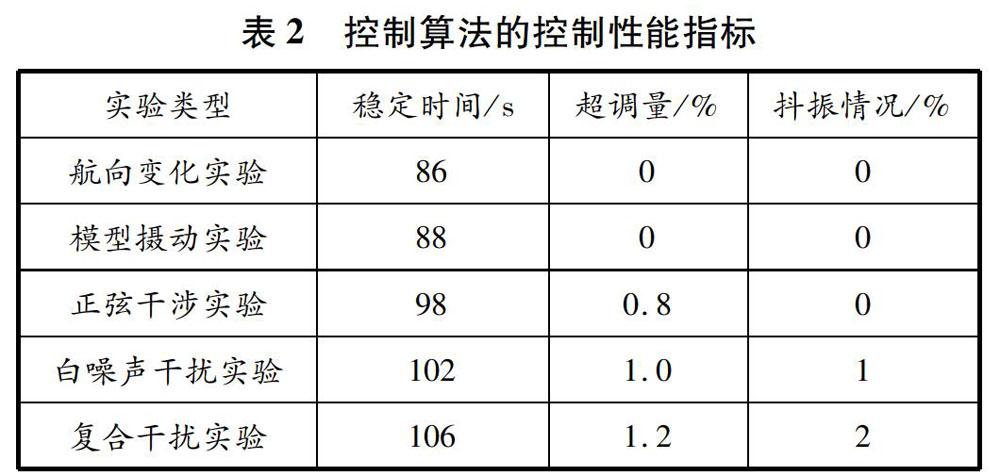
表2為在各種實驗條件下船舶運動控制的具體結果。航向變化實驗中，一階響應模式用于執行跟蹤實驗，振幅為30°，實驗初始值為0°，無干擾;模型攝動實驗與航向變化實驗的區別在于系統參數中增加了擾動項，USV的參數值受到了40%的擾動;正弦干涉實驗與航向變化實驗的區別在于增加了外部正弦波干擾，系統輸出受到振幅為2°、頻率為0.1 rad/s正弦波的干擾;白噪聲干擾實驗與正弦干涉實驗的區別在于外部干擾改為白噪聲，系統輸出受到幅度為0.1的白噪聲干擾;復合干擾實驗與航向變化實驗的區別在于增加了復合外部干擾，USV的參數值受到40%的干擾，且系統輸出受到幅度為0.1的白噪聲干擾。控制性能指標滿足了工程設計要求，驗證了智能控制算法的有效性和實用性。

4.3 對比實驗

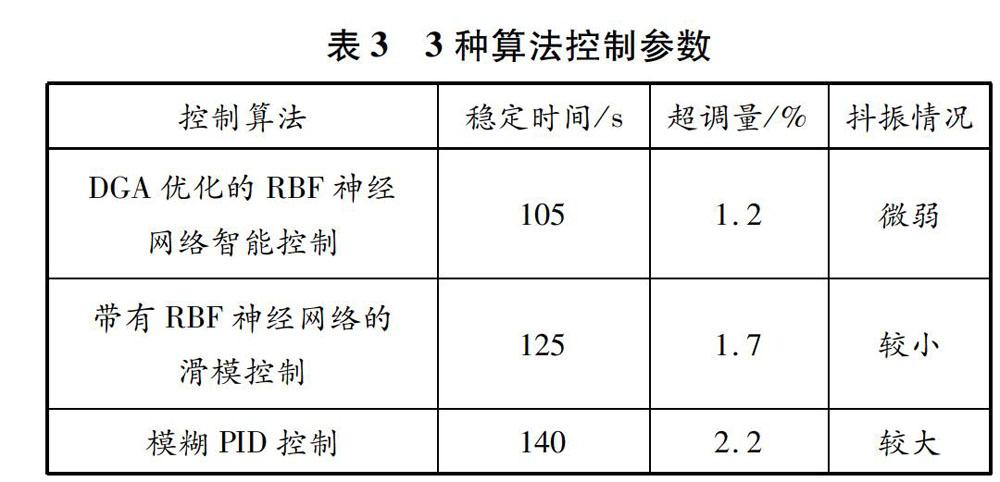
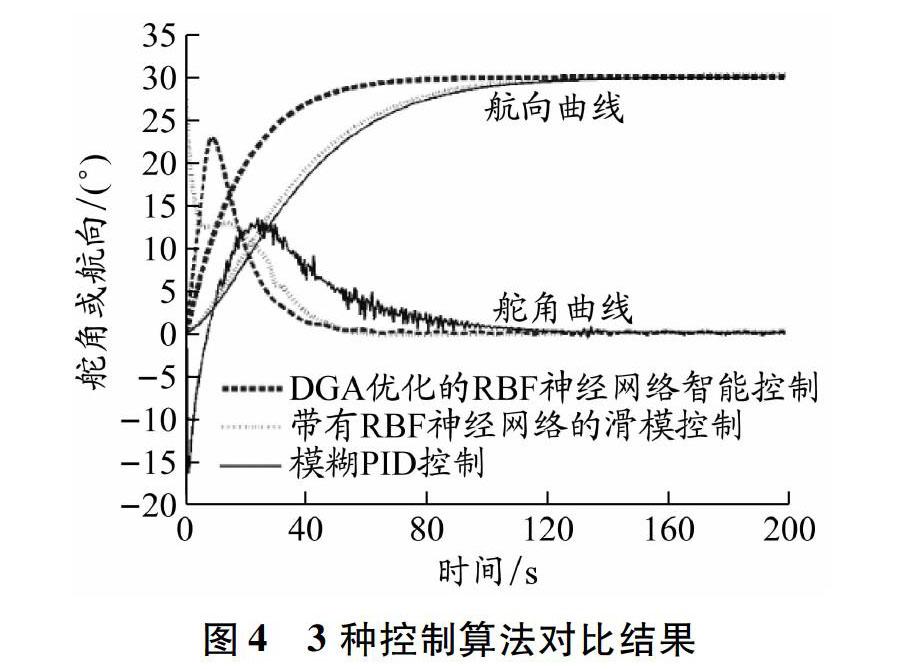
通過與文獻[3]和文獻[11]提出的兩種控制算法進行比較，可以驗證本文設計的智能控制算法的先進性。實驗初始航向為0°，跟蹤航向為30°，外界風浪干擾近似用白噪聲隨機干擾替代，軌跡跟蹤對比實驗結果見圖4，控制參數對比見表3。

4.4 結果比較與驗證

從表3可以看出，模糊PID控制的穩定時間約為140 s，帶有RBF神經網絡的滑模控制的穩定時間約為125 s，本文設計的智能控制的穩定時間約為105 s。與模糊PID控制和帶有RBF神經網絡的滑模控制相比，本文設計的智能控制更加先進，系統達到穩定的時間更短，平均超調量更小。可以看出，由DGA優化的RBF神經網絡的逼近速度更快。

在工程實踐中，抖振越弱，控制系統就越穩定和可靠。因此，DGA優化的RBF神經網絡智能控制算法的控制性能是最好的。

由圖4可知：文獻[3]中不采用抗飽和技術的模糊PID控制輸出最初達到35°，經過一定時間后離開飽和區，抖振較大;文獻[11]中帶有RBF神經網絡的滑模控制輸出在開始時就離開了飽和區，經過小幅振蕩后達到了控制效果，抖振較小;本文設計的智能控制的最大控制輸入小于25°，達到了快速控制的效果，抖振微弱，達到穩定需要的時間也最短。因此，在相同的外界干擾下，DGA優化的RBF神經網絡智能控制算法的穩定時間最短，且抖振最弱。

5 結 論

分布式遺傳算法（DGA）能夠保證搜索的充分性和全局最優收斂結果。將帶有模擬退火（SA）算法的DGA應用于徑向基（RBF）神經網絡的參數優化以提高逼近性能。結合RBF神經網絡及干擾觀測器，利用滑模控制方法設計了船舶運動智能控制算法。實驗結果表明，DGA優化的RBF神經網絡智能控制算法比模糊比例積分微分（PID）控制算法和帶有RBF神經網絡的滑模控制算法更有效。需要說明的是，本文未考慮船舶慣性大造成的輸出延遲問題，今后將針對該問題進行進一步探討。

參考文獻：

[1]MA Liyong， XIE Wei， HUANG Haibin. Convolutional neural network based obstacle detection for unmanned surface vehicle[J]. Mathematical Biosciences and Engineering， 2019， 17（1）： 845-861.DOI： 10.3934/mbe.2020045.

[2]沈海青. 基于強化學習的無人船舶避碰導航及控制[D]. 大連： 大連海事大學， 2018.

[3]馮永孝， 張顯庫. 基于非線性修飾模糊PID的船舶航向保持控制[J]. 船舶工程， 2018， 40（S1）： 202-205.DOI： 10.13788/j.cnki.cbgc.2018.S1.202.