基于記憶效應的社交網絡信息傳播模型

王曉萌， 方濱興， 張宏莉， 王 星

(哈爾濱工業大學 計算機科學與技術學院, 哈爾濱 150001)

0 引 言

在線社交網絡與生俱來的自由性和開放性，使其逐漸成為當代社會信息傳播的重要集散地，社交網絡中的信息活躍性達到了前所未有的程度。隨著國內外大量在線社交網絡服務的涌現以及用戶的參與，針對社交網絡信息傳播分析的相關研究引起了國內外學者的高度關注。研究社交網絡中的信息傳播規律，建立傳播模型，即能從信息傳播的角度對網絡結構、屬性以及突發事件遵循的規律有進一步的認識。

信息傳播模型是信息傳播研究內容的核心，主要任務是分析信息傳播過程中的影響因素，理解、模擬并驗證擴散過程。信息傳播與疾病、文化和行為的傳播是人類社會中常見的現象，很多研究者多借鑒病毒傳播模型[1-2]來研究在線社交絡中的謠言傳播[3-4]。傳統的傳染病傳播模型中的狀態表征存在不足，個體只有感染、易感和免疫三種狀態，許多擴展模型并沒有充分考慮信息傳播的內在機理與用戶的影響力，傳播模擬實驗結論也沒有給出拓撲結構對傳播機理影響的合理解釋。信息傳播具有記憶效應(memory effect)[5]，記憶效應是指人對于同類信息接觸所具有的記憶上的累積特性，即同一類信息的多次冗余接觸會改變人們對其初始看法，這種累積特性會對社交網絡中用戶的轉發行為產生影響。部分在線社交網絡上的實證研究[6]已經驗證的記憶效應在社交網絡信息傳播過程中存在且具有規律性。

以往的傳播模型大都沒有考慮記憶效應這種行為對傳播的影響或考慮不全面。本文中，將同時考慮傳播過程中的記憶效應的興趣累積與時效衰減兩方面，還將兼顧社交網絡中用戶影響力，對在線社交網絡中的信息傳播行為進行詳細的理論建模與數值仿真，有助于深入理解社交網絡中的傳播行為，為輿情研究提供理論基礎。

1 相關工作

社交網絡中記憶效應的研究最早來自于Centola的郵件推薦實驗[5]，Centola將1 528名的注冊用戶以匿名的方式分配到度相同的規則網絡(最近鄰耦合)與隨機網絡[7]中，每個用戶通過郵件的方式對鄰居用戶重復推薦一個健康社區網站，當個體接收到多次郵件推薦后，則更有可能接收該郵件的推薦內容并進行轉發。而在此之前，傳統結論一般認為具有短平均路徑的隨機網絡更有利于信息的傳播，但在線社交網絡存在記憶效應，與此同時還發現相比于平均路徑較短的隨機網絡，具有高聚集系數的規則網絡更有利于行為的傳播與擴散。

隨后，Romero等人[6]對大量Twitter數據進行統計分類，發現不同類型話題傳播過程中記憶效應的的巔峰概率與接受信息次數的關聯關系。文獻[8]對海量新浪微博數據進行統計，發現不同類型的微博在轉發過程中所表征出來的記憶效應曲線存在差異，冗余的信息刺激可能會降低微博的轉發概率。Myers等人[9]認為社交網絡用戶影響力可以近似擬合為一個與信息累積接受次數相關的曝光曲線(exposure curve)。文獻[10]建立了一個興趣積累的記憶效應傳播模型，并討論該模型在小世界網絡上的傳播能力，但該模型只考慮了記憶效應帶來的概率累積一種情況。

相對于之前的研究，本文將整合上述研究者的工作，探究符合記憶效應規律的信息傳播特征，借鑒傳染病模型，重新劃分社交網絡上節點的狀態集，給出傳播動力學方程并在模擬網絡與真實網絡上進行驗證分析。

2 傳播機理與模型

在線社交網絡中，用戶發布或分享的信息會傳遞給該用戶的好友，其好友會依據興趣程度、是否可信、新鮮程度以及傳播源的影響力等因素以一定概率對信息進行轉發擴散。然而信息多次累積會產生記憶效應，對用戶的轉發行為產生影響，研究中給出了2個過程的表征含義可分述如下。

(1)興趣累積。在社交網絡中，愛好、謠言以及一些信息真實性辨識度不高的信息在傳播過程中一般表現出興趣累積的記憶效應，即接收到同類信息刺激越多，用戶越易產生轉發行為。如圖1中所示“事件一”[8]的傳播概率隨著被推薦次數的累積而增加，近似呈現指數式遞增。

(2)時效衰減。即時性強的突發新聞，社交網絡用戶越少接觸，則轉發的意愿越強烈。若社交網絡用戶在某一時刻收到多次轉發，則用戶的興趣度就會隨時間衰減，不易再產生轉發意圖。如圖1中即時性很強的新聞“事件二”[8]，轉發該條微博的用戶一般初次收到就轉發，隨接觸次數增多轉發概率便逐步遞減。

本節將首先提出一種涵蓋以上兩種記憶效應表征的統一模型，兼具興趣累加與時效衰減兩種特點。該模型中，信息要經過興趣累積過程，傳播概率在多次接觸后會達到峰值，而當經歷了時效衰減過程，傳播概率逐漸降低，概率函數性質符合圖1中曝光度曲線。在此基礎上將在線社交網絡節點劃分為4種狀態，其狀態間的轉移概率以及傳播過程如圖2所示。本節中涉及到的縮寫和符號的含義見表1。

圖1 新浪微博中信息傳播的記憶效應

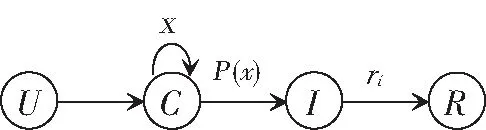
圖2 狀態轉移示意圖

表1 相關符號含義

Tab. 1 Related symbol meaning

符號(縮寫)含義G社交網絡拓撲V整體拓撲點集E整體拓撲邊集P(x)收到信息第x次后轉發的概率α累積效應峰值β傳播轉發過程中所能達到的巔峰概率ri節點i由傳播態轉為疲勞態的概率Ci節點i的個體影響力強度deg(i)節點i的度R終態時網絡中疲勞態的數量b影響力差異系數

2.1 節點狀態

社交網絡形式化描述為G=(V，E)，其中G代表社交網絡，V是點的集合，表示社交網絡上的用戶，E為邊的集合(無向邊)，表示用戶間的好友關系。借鑒SIR模型的思想，將社交網絡中節點的類型拓展為4種狀態，每一時間步，每一個體處于如下4種狀態之一：

(1)未知態U(Unknown)。不知道消息的人群，類似于SIR模型中的易感人群。

(2)積蓄態C(Cumulative)。用戶聽到了這個信息，但是由于不確定信息的準確性或者已經變得不感興趣而不愿意傳播。

(3)傳播態I(Infected)。個體確認了該消息并將該信息擴散給其鄰居。

(4)疲勞態R(Resistant)。個體傳播了信息后失去繼續傳播該類話題興趣的人群，相當于SIR模型中的免疫態。

2.2 狀態間遷移概率

(1)傳播概率。假設積蓄態節點轉變為傳播態節點的概率服從如圖1所示的曝光度曲線，曲線方程定義如下：

(1)

其中，x為截止到t時刻，個體累計接收到的信息次數，反映了信息傳播的記憶性特征；P(x)為用戶第x次接收到其鄰居轉發的信息后選擇轉發的概率；β∈(0,1]為該類型信息最流行時的傳播概率峰值，稱之為巔峰概率；α∈N*為P(x)=β時的轉發次數，稱α為累積效應峰值。

當累積峰值α=1時，所對應的信息類型為具有時效衰減性質的即時新聞，接觸次數越多用戶越易失去轉發興趣，傳播概率方程退化為式(2)：

P(x)=βx·exp(1-x),

(2)

(2)恢復概率。社交網絡信息傳播過程中的另一個重要因素就是用戶影響力，影響力大的用戶發布的信息往往具有較長的持續時效。影響力越大，用戶對其鄰居施加的持續影響力越大，相對應模型中傳播態變為疲勞態的時間就越長，其函數關系如式(3)所示：

ri=exp(-b·Ci),

(3)

其中，ri為節點i由傳播態變為疲勞態的轉移概率，b∈[0,)為影響力差異系數，用于刻畫不同用戶節點間影響力差異程度。當b=0時，用戶間影響力不存在差異，ri=exp(0)=1，傳播態節點只對鄰居節點轉發一次信息便失效，每條邊只使用一次，類似于信息快速更新的微博網絡。Ci為節點i的影響力強度，這里研究采用直接反映社交網絡用戶人際關系的點度中心度(degree centrality)來表示節點直接影響力；deg(i)為節點i的度，則節點i的影響力強度如式(4)所示：

Ci=deg(i)，

(4)

將式(3)帶入式(2)得：

ri=exp(-b·deg(i)).

(5)

2.3 傳播建模

模型中，假定傳播過程開始前網絡上所有節點均處于未知狀態。當社交網絡上的用戶發布或轉發信息的同時，會擴散給其所有的好友，即隨機選取一個種子節點，這個種子節點在每次給其所有的鄰居發送信息后都以ri的概率置為疲勞態。在每個時間步內，如果一個節點(未知態或積蓄態)收到信息，都將立刻變為積蓄態，并以概率P(x)變為傳播態，這里x是指個體已經接收到信息的次數。當x≤α時，P(x)的值隨信息接收次數x的增加而單調遞增，并在x=α時達到最大。當x>α時，P(x)的值隨信息接收次數x的增加而單調下降。因此，轉發概率的大小不僅依賴接收信息的次數，也取決于信息本身的特性。如果一個節點在某個時間步內轉變為傳播態，就將在下一個時間步把信息發送給其所有的鄰居，同時以概率ri變為疲勞態。如果一個處在積蓄態的節點，在當前的時間步沒有接收到任何信號，無論已經接受到信息的次數x為多大，都將不會發生任何狀態上的改變。詳細步驟如下。

輸入: 網絡拓撲G=(V，E)、巔峰概率β、累積峰值α

輸出: 終態的疲勞態節點集R

Step1將所有N個節點初始化為未知態。

Step2從N個未知態節點中隨機選取一個節點置為傳播態。

Step3所有傳播態節點向其所有鄰居轉發消息，這些鄰居節點中處于未知態的節點變為積蓄態，曝光度x=1；積蓄態個體曝光度x=x+1。

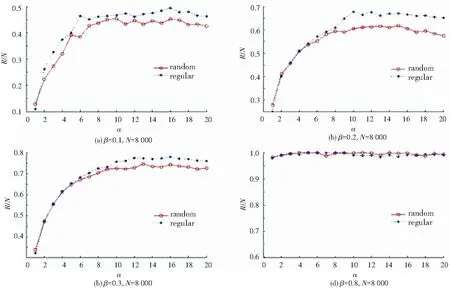
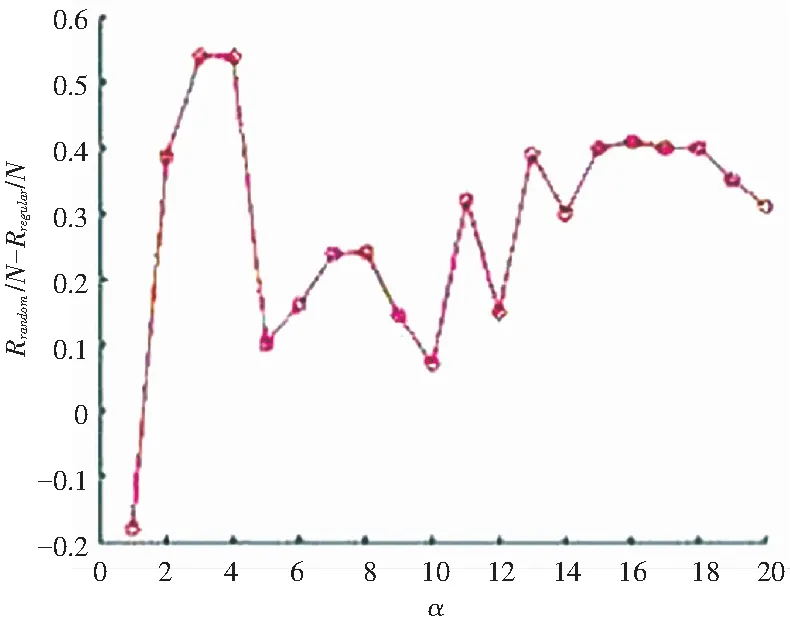
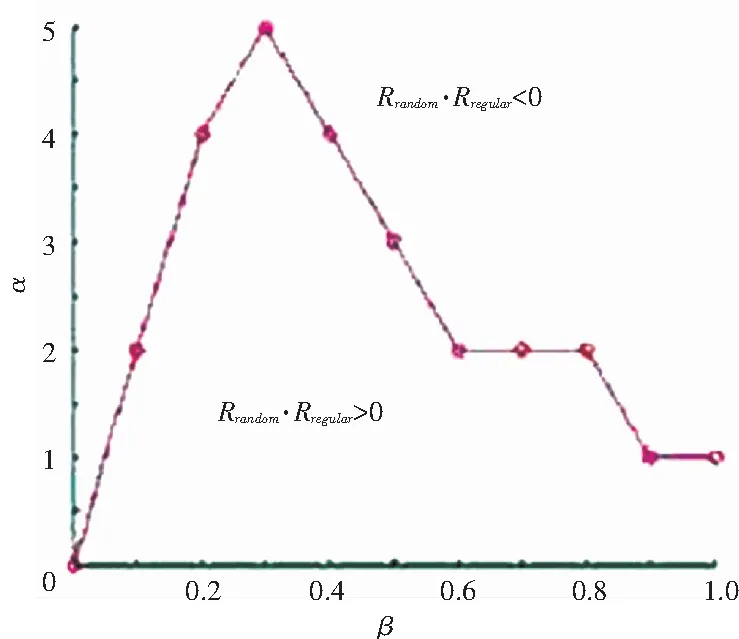
Step4檢查所有積蓄態節點，若隨機數random[0,1]

Step5檢查所有傳播態節點，若隨機數random[0,1]

Step6循環Step 3～Step 5，直至網絡中不存在傳播態節點。

3 仿真實驗

3.1 數據集

在線社交網絡中存在許多高聚集性的社區，朋友圈等。社區內部緊密相連，類似規則網絡。而不同的社區間又通過一些共享用戶隨機地鏈接在一起。這使得在線社交網絡兼具高聚集系數與短平均路徑。已有模型如BA模型[11]、WS模型[12]及一些拓展模型，這些模型雖然宏觀上表述了在線社交網絡的小世界現象與無標度特性，但都不能完全表征在線社交網絡的拓撲特征。Centola的電子郵件實驗從宏觀的角度說明了相比于具有較短平均路徑的隨機網絡，高聚集系數的規則網絡更有利于行為在人際社會中的傳播。為了驗證這一結論，研究將首先在規則網絡與隨機網絡兩種均勻網絡拓撲上驗證本文模型的傳播演變過程。

此外，本文選取國內較流行的大學生社交網絡人人網的用戶數據作為非均勻網絡數據，該網絡上的節點為注冊用戶，用戶間的好友關系表示為邊。研究建立了一個基于網頁解析方式的爬蟲程序，首先選取多個同一所學校的用戶作為種子節點，遞歸地爬取每個種子用戶的好友關系，及其好友的好友關系。然后將爬取得到的多個好友網絡進行拼接與去重，并且對不屬于種子節點注冊學校的其它節點以及邊的關系進行刪除，最終得到一個包含8 102個節點、45 776條邊的的最大聯通子圖。各網絡的拓撲參數見表2。

表2 各網絡的結構參數

3.2 仿真結果

分別選取節點數N=8 000，平均度k=11的規則網絡與隨機網絡，影響力差異系數b=0.2，迭代次數T=500。圖3中列出了隨著巔峰概率β取不同值時，規則網絡與隨機網絡上疲勞態節點的比例隨累積峰值α變化的情況，對每組數據的結果都是進行500次獨立重復模擬求均值得到的。當累積峰值α=1時，對應具有時效衰減類型記憶效應的即時新聞，由圖3(a)～(c)可以看出，當α=1，β取0.1，0.2，0.3時，隨機網絡的R值均略大于規則網絡，這是由于規則網絡的聚集性強，時效衰減的效果更容易積累，阻礙了傳播。同時，研究還可以觀察到，隨著峰值概率β的上升，規則網絡與隨機網絡的擴散規模均呈現增加趨勢。當β=0.8時，圖3(d)中規則網絡與隨機網絡的傳播規模都幾乎覆蓋了全部節點。由此可以認為，當峰值概率的值上升到一定程度時，聚集系數與平均路徑長度這兩個網絡拓撲特征已不能左右信息的傳播，信息都將擴散至全部網絡。

疲勞態節點密度差值比例與α的變化關系如圖4所示。由圖4可見，當β=0.1，N=8 000，累積效應峰值α>1時，規則網絡的傳播范圍Rrandom均大于隨機網絡的傳播范圍Rregular。聯合圖3(a)進一步分析可發現，1<α<5時，Rregular-Rrandom呈明顯遞增趨勢，規則的傳播優勢更加明顯；當5≤α≤10時，Rregular-Rrandom呈現波動性變化；當α>10后，Rregular-Rrandom幾乎維持不變。

此外，可以從圖3中發現，總是存在臨界值αc，使得當1≤α<αc時，Rrandom>Rregular；α>αc時，則Rrandom≤Rregular。保持節點數量N=8 000不變，臨界值αc相對于巔峰概率β變化規律如圖5所示。

圖3 疲勞態節點最終密度隨累積峰值α變化的關系

圖4 疲勞態節點密度差值比例與α的變化關系

Fig. 4 The relationship between the ratio of the difference in fatigue state node density andα

圖5 臨界值αc隨巔峰概率β的變化關系

Fig. 5 The relationship between the critical valueαcand the peak probabilityβ

由圖5可以看出αc隨著β先增大后減小，當β=0.3時，maxαc=5。這說明當記憶效應呈現出興趣累積特征時，若這種特征不明顯，隨機網絡也有可能比規則網絡更適合傳播，而Centola的規則網絡優于隨機網絡的結論在這種場景下并不適用。

除了傳播過程中的巔峰概率α與累積效應峰值β外，另一個重要的影響因素是網絡的規模N。研究中保持巔峰概率β=0.1，網絡平均度k=11不變，在100～8 000間不同網絡規模N上分別對α=1，α=10，α=20這三種取值進行實驗模擬。如圖6所示。研究分析發現當N≤500時，隨機網絡總是優于規則網絡。這是由于規模小的網絡，節點彼此間收到信息次數差異不明顯。而在網絡規模N>500后，α=10與α=20對應的曲線總體上都呈現上升趨勢。這是因為網絡規模N上升，隨機網絡的聚集系數/N隨之下降，而規則網絡聚集系數恒定的優勢逐漸顯現出來，這使得單個節點的信息接收次數更易積累，這與Centola的行為傳播實驗結論是一致的。

在線社交網絡的度分布是不均勻的，分別選取人人網數據集中度最大的節點kmax=221與度最小的節點kmin=1為初始傳播節點。當α=1，N=8 102時，在線社交網絡中處于疲勞態R的節點占總數量N的比值隨時間變化情況用R(t)/N表示，如圖7所示。可以發現，網絡規模均為N=8 102時，在線社交網絡上的信息傳播速度要快于隨機網絡與規則網絡，這是由于社交網絡中存在一些度較大的節點，使信息得以快速擴散。還可以發現，初始節點的選擇對信息傳播的規模存在影響，度較大則達到的最終傳播規模更大，但這種規模并沒有超越隨機網絡，而是介于隨機網絡與規則網絡之間，這說明在聚集系數低的隨機網絡上記憶效應更不容易累積。

圖6 疲勞態節點數量差值比例與網絡規模的關系

Fig. 6 Relationship between the ratio of the difference of fatigue state nodes number and the network scale

圖7 初始節點度最大與度最小情況下的傳播情況

Fig. 7 Propagation of the maximum degree and the minimum degree of initial node

4 結束語

本文首先討論了在線社交網絡上信息傳播的記憶效應，及其不同表征過程。然后針對社交網絡上傳播行為的記憶效應與個體影響力對傳統傳染病模型進行改進，并在此基礎上設計提出了基于記憶效應的在線社交網絡傳播模型。再由模擬網絡與人人網數據集合搭建的實驗網絡中對信息傳播進行仿真，實驗結果表明，該模型能夠表征在線社交網絡的傳播特性，并且信息在不同結構網絡上的傳播效果存在差異，對此可表述如下。

(1)具有時效衰減特征的信息在隨機網絡上進行傳播更廣，拓展了Centola的實驗結論。

(2)謠言、愛好等具有興趣累加類型記憶效應的信息更容易在規模較大規則網絡上傳播，如學校的在線社區，且這種趨勢會隨著網絡規模與累積峰值的增大而更加顯著。

本文研發提出的模型針對的是單一信息的獨立傳播，而真實社交網絡中信息是多種類且并行傳播的，會產生互相影響，從而與獨立信息的傳播規律不同。研究多信息傳播的規律并建立驗證模型將是今后的研究方向。