雙軌火箭橇全時程動力學仿真分析研究

顧凱旋，龔明生，王磊，熊闖

(1.航空工業航宇救生裝備有限公司 試驗部，襄陽 441003) (2.北京航空航天大學 固體力學研究所，北京 100143)

0 引 言

火箭橇是在專用的軌道上，推動滑車高速前進以獲取模型試驗測試數據的大型地面動態試驗系統。由于這種試驗技術能夠模擬飛行狀態，已成為現代武器所有地面試驗設備中比較有效的一種特殊試驗手段[1-3]，可以解決飛機、導彈、宇航飛行器及其他武器或機械設計在研制過程中有關高速度、高加速度可能帶來的許多技術問題。然而火箭橇的振動問題，往往過載都超過500g，這對于試驗的準確性和安全性都有較大的影響[4-5]。因此，研究火箭橇的振動問題具有理論意義和實用價值。

雙軌火箭橇在載重方面優于單軌火箭橇，但是雙軌火箭橇由于軌道不平順所引起姿態振動的理論分析研究工作也遠遠要復雜于單軌火箭橇。當前針對火箭橇動力學響應的研究正處于起步階段，S.I.Gerasimov等[6]對橇軌之間的橇軌接觸變形及運動穩定性進行了分析；D.J.Laird等[7-8]對高速火箭橇滑靴-滑軌撞擊過程進行了仿真分析，并建立了二維平面下滑靴-滑軌的交互耦合模型；J.H.Zhang等[9]對火箭橇剛柔耦合模型的動力學分析進行了研究。相比而言，國外動力學分析方法較為成熟且發展了相應的分析軟件，而國內目前針對火箭橇動力學分析的理論還不完善。王健等[10]對火箭橇軌道不平順功率譜密度進行了分析；董治華等[11]對火箭橇減振系統進行了分析；楊珍等[12]對單軌火箭橇的載荷預示技術進行了研究；張雨詩等[13]對火箭橇軌道系統有限元建模及振動特性進行了研究。然而以上研究均是對火箭橇系統的各個子模塊進行了研究，針對火箭橇系統的動力學分析理論仍然匱乏，尤其是針對雙軌火箭橇，關于其動力學分析的研究鮮有報道。系統地研究雙軌火箭橇振動行為，分析其在試驗各時刻的振動響應，是火箭橇理論研究與試驗領域亟待解決的重大問題。

本文針對雙軌火箭橇系統，建立橇軌-滑車系統的動力學分析模型。首先對真實模型進行模態分析，通過優化方法，采用梁單元建立橇車三維實體模型的簡化模型。在此基礎上，推導綜合考慮阻尼、橇軌間隙以及不平順度的火箭橇運動動力學方程并進行求解。在已有的研究經驗基礎上，以期進一步豐富火箭橇動力學分析理論。

1 滑車模型簡化

滑車模型復雜，動力學計算規模巨大。在分析時需要對其進行必要的模型簡化，在保證模型動力學特性基本不變的前提下，降低模型的復雜程度，從而提升計算效率。

根據滑車的模型圖，對其進行網格劃分，得到滑車有限元模型如圖1所示。根據其幾何特征，得到其簡化模型如圖2所示，其中，各部分均采用梁單元來模擬。

圖1 雙軌火箭橇滑車有限元網格模型Fig.1 Finite element model of two-track rocket sled

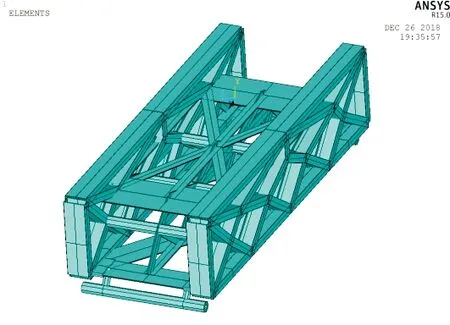
圖2 雙軌火箭橇簡化模型Fig.2 Simplified model of two-track rocket sled

對簡化模型進行修正，得到簡化模型與真實模型前5階頻率對比如表1所示。簡化模型與真實模型前5階模態振型也基本一致，因此，對模型的簡化取得了較好的效果。

表1 簡化模型與真實模型頻率對比

2 動力學計算分析

2.1 計算輸入

由于火箭橇-滑車的振動主要為垂向及側向的振動。對于航向，火箭橇存在大范圍剛體運動與小量級的結構振動，小量級振動變形較小且不影響關注問題的結果，故可忽略，因此可將火箭橇的航向運動簡化為剛體運動。根據實測數據得到滑車航向速度曲線如圖3所示。

圖3 航向速度曲線Fig.3 Curve of course speed

根據測點位置對軌道不平順值進行測量，對于不平順表達的輸入參數只需獲得實際的軌道不平順值與監測點間隔。根據軌道不平順數據能夠得到任意位置軌道的不平順值及其斜率。軌道不平順值d的計算公式和軌道不平順斜率kd的計算公式分別為

(1)

kd=d/l1

(2)

式中：dn+1為當前滑塊位置后一個軌道監測點的不平順監測值；dn為當前滑塊位置軌道前一個監測點的不平順監測值；l1為當前滑塊位置距離前一個觀測點的長度；L為監測點間隔長度。

2.2 橇-軌碰撞接觸力計算

在火箭橇動力學仿真中，采用L-N非線性接觸力模型計算軌道與橇車滑塊之間的橇-軌接觸力。L-N非線性接觸力模型可寫為如式(3)所示：

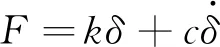
(3)

橇-軌碰撞接觸力求解流程如圖4所示，接觸力計算流程如下：

(1) 由橇車的航向運動確定當前時刻橇車各滑塊在軌道中的位置和橇車的運動速度；

(2) 由滑塊當前位置確定軌道不平順值和不平順斜率，進而確定橇車滑塊與軌道接觸狀態；

(3) 由上述步驟判斷得出接觸變形和接觸變形速率，調用式(3)所示的接觸力模型即可計算當前時刻的橇-軌碰撞接觸力。

圖4 橇-軌碰撞接觸力求解流程Fig.4 Flowchart of solution of skid-rail collision contact

2.3 動力學仿真計算方法

綜合考慮橇車的垂向振動、橫向振動和航向剛體運動，火箭橇的振動的有限元方程可寫為

(4)

阻尼矩陣C采用瑞利阻尼模型，即：

C=αM+βK

(5)

式中：α及β的取值根據文獻[14]所給方法求得；簡化模型的總體質量矩陣M和剛度矩陣K利用ANSYS提取。

(6)

(7)

式中：γ和δ是按積分精度和穩定性要求決定的參數。

當γ=1/4和δ=1/2時，Newmark方法退化為常平均加速度法這樣一種無條件穩定的積分方案。此時，Δt內的加速度為

(8)

Newmark方法中的時間t+Δt的位移ut+Δt是通過滿足時間t+Δt的運動方程得到的。

從公式(7)可得：

(9)

根據

(10)

(11)

全時程動力學求解流程如圖5所示，求解步驟為：

(1) 初始化計算，設定計算總時間T，計算時間步長Δt。設置當前時間步為t=0(即初始時刻)，獲取航向運動初始位置、速度和加速度，垂向和橫向運動初始位置、速度和加速度。

(2) 由t時刻航向運動得到航向的位移，速度與加速度。

(3) 由t時刻滑塊的航向位置，結合軌道不平順值和不平順斜率，得到當前的接觸變形與接觸變形速率。通過調用橇-軌碰撞接觸力計算模塊，判斷滑車各個滑塊與軌道的碰撞接觸情況并計算當前時刻垂向和橫向的橇-軌碰撞接觸力。

(4) 由當前運行時間t、橇車航向速度以及橇-軌碰撞接觸力確定橇車當前時間步的其他各項外載荷輸入條件。

圖5 動力學仿真計算流程Fig.5 Flowchart of the dynamics simulation calculation

(5) 通過調用Newmark數值積分方法求解橇車動力學方程(即式(5))，得到t+Δt時刻橇車的垂向和橫向位移、速度以及加速度響應。

(6) 令t=t+Δt，判斷t是否大于總時間T，若t≤T，則返回步驟(2)繼續進行動力學仿真計算，否則結束計算。

2.4 動力學計算結果

取航向速度最大段結果進行分析，本文僅給出了其中一個滑塊的結果，其余三個滑塊的結果基本相同。滑塊處垂向碰撞接觸力、垂向過載及功率譜密度曲線如圖6～圖8所示。

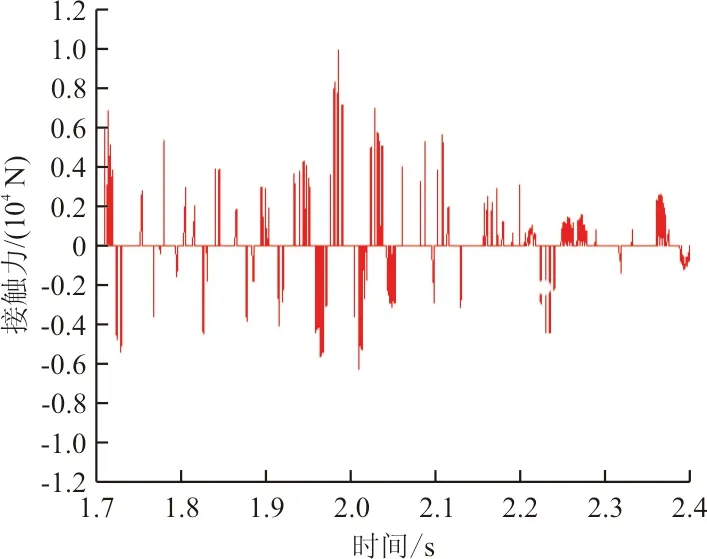
圖6 碰撞接觸力曲線Fig.6 The curve of the collision contact force

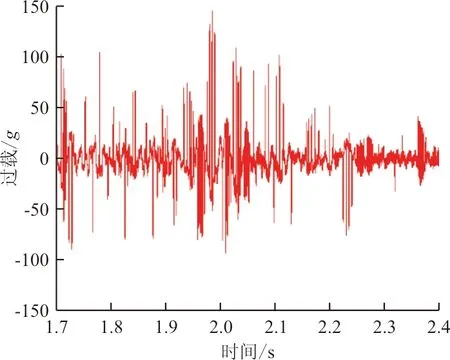
圖7 滑塊垂向過載曲線Fig.7 Vertical overload curve of the slider

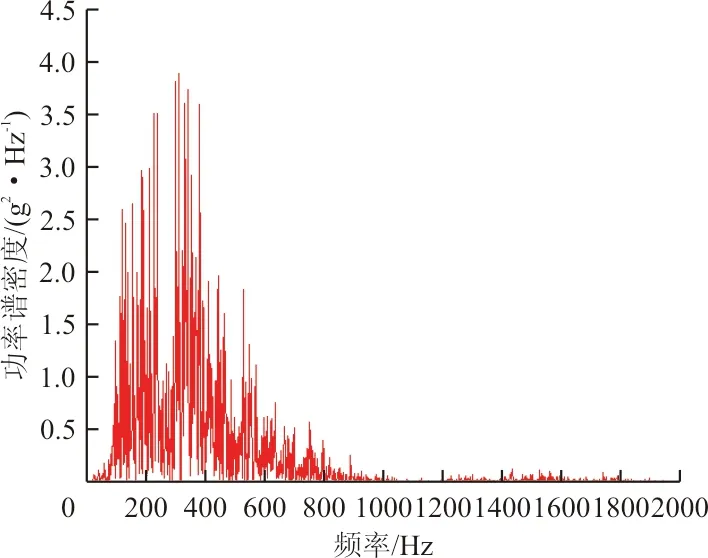
圖8 滑塊垂向加速度功率譜密度曲線Fig.8 Vertical acceleration power spectral density curve of the slider

由于本文所計算的車體未進行試驗，采用速度基本相同的火箭橇振動響應的試驗結果進行了對比，試驗數據如表2所示。

表2 火箭橇試驗振動響應結果

從上述結果可以得到以下結論：

(1) 滑塊處過載曲線峰值出現在滑車運行速度較大的時刻。由于滑車速度快，單位時間內滑靴所經歷的軌道不平順變化較大，使得滑靴與軌道的碰撞接觸力增大。因此隨著滑塊航向速度的增大，過載也變大。其峰值過載為140g，與速度基本相同的火箭橇試驗實測得到的130g基本吻合，說明計算所得的數據有一定的可信性。

(2) 各測點振動能量主要集中在0～800 Hz，1 000 Hz以后振動非常微弱，與速度基本相同的火箭橇試驗實測結果基本一致，驗證了本文所提出方法的正確性。

3 結 論

(1) 本文采用梁單元對真實模型進行了簡化，通過對比簡化模型與真實模型的前5階頻率及模態振型，表明簡化模型復雜度低，計算效率高。

(2) 推導了考慮阻尼、橇軌間隙以及不平順度的火箭橇運動動力學方程組，并通過數值方法對雙軌火箭橇系統進行了全時程動力學響應求解。仿真分析結果與速度基本相同的火箭橇試驗實測結果基本吻合，驗證了本文采用的仿真分析方法的合理性。

本文所采用的仿真分析方法可用于試驗前對雙軌火箭橇進行動力學分析，對試驗結果有提前的預判。在計算中模型簡化以及計算參數的設定會帶來計算誤差，因此，該仿真分析方法僅僅能得到一個量級正確的粗略結果，要得到火箭橇系統精確的動力學響應，還是要借助試驗。