轉換問題視角，拓展思維的廣度和深度

唐志忠

(江蘇省常熟市中學 215500)

“山窮水復疑無路，柳暗花明又一村”是指在前進道路上遇到重大挫折，甚至陷入絕境時，只要有新的發現，就會迎來巨大轉折，甚至出現新的奇跡.在生活中，如果矛盾的雙方能換位思考，即從對方的立場來思考，那么矛盾就會迎刃而解.在高中數學教學中，也會出現類似問題.如某個問題比較繁復而難以解答時，若能適時轉換視角，重新審視問題，問題往往會迎刃而解，這就是轉換視角的益處.

思維的廣度和深度是思維的兩個重要特性.培養學生思維的廣度要強化一題多解,重視一題多變.訓練學生思維的深度,要培養學生追根溯源的習慣,并注重知識的系統性.本文通過案例談談轉換視角拓展思維方向、廣度和深度的方法，望對讀者起拋磚引玉的作用.

1 從參變量的地位著手，展現思維的廣度

案例1設不等式mx2-2x-m+1<0對任意的m∈[-2,2]都成立，求x的取值范圍.

本題提供了四種解法，從中可以看出交換參變量的優勢所在.

方法1 分類討論

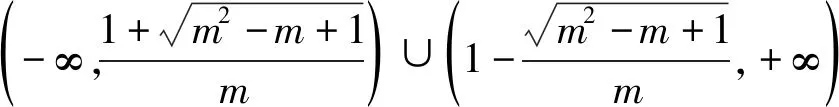
學生做到這里,往往不知道如何找到同時屬于上述三個集合的x的取值范圍.

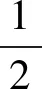
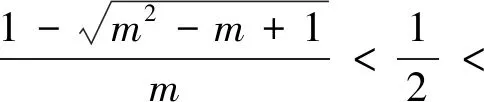
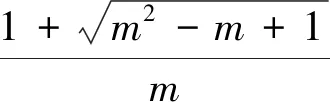
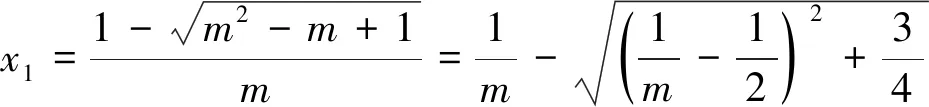
方法2 變量分離

原不等式可化為m(x2-1)<2x-1.

當x=1時不等式恒成立；當x=-1時不等式不成立.

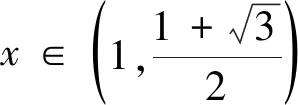
方法3 數形結合

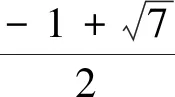
方法4 交換參變量的位置，把m看作主元

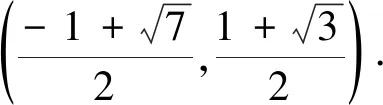
上述四種方法中，學生往往首選方法1，但此法計算比較復雜，且容易考慮不全面；方法2同樣是變量分離后進行分類討論，比方法1簡單一些；方法3對思維要求比較高；而方法4通過轉換參變量的地位，拓展思維的廣度，達到了節省時間、化繁為簡的目的.通過比較四種方法，學生普遍覺得方法4最好：通過視角的轉化，豐富了知識，開闊了視野.

2 從問題的對立面著手，體現思維的方向

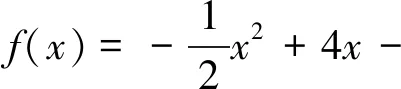
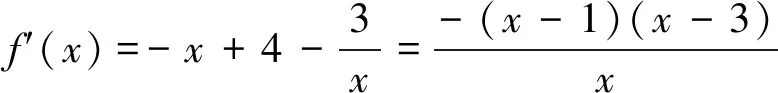
3 從問題的數學本質視角著手，拓展思維的深度

案例3(江蘇省2017高考第20題)已知函數f(x)=x3+ax2+bx+1(a>0,b∈R)有極值，且導函數f′(x)的極值點是f(x)的零點(極值點是函數取極值時對應的自變量的值).

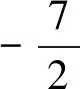
解析 (1)(2)略.

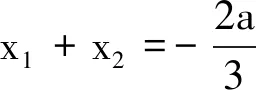
“轉換視角天地寬”，轉換數學問題的視角能讓學生從不同角度探究問題，能夠加深學生對問題本質的認識、拓展思維方向、拓寬思維廣度、拓深思維深度，對培養學生邏輯推理素養、形成靈活應用知識解決問題的能力、培養學生的創造力具有重要的意義.