基于STM32的步進電機動態加減速控制

何昌俊， 楊自棟， 閆珍奇， 曾 恒

(浙江農林大學 工程學院， 浙江 杭州 311300)

步進電機是一種可將電脈沖信號轉變為角位移或線位移的開環控制元件。工作時，每輸入一個脈沖，電機轉軸即可轉過一個相應的步進角，具有精度高、運行可靠及無累計誤差等優點，因而被廣泛應用于數字控制系統中。理論上，步進電機的工作狀況只和脈沖數和脈沖頻率相關。在實際中，隨著脈沖頻率的升高，步進電機轉矩隨之降低，當頻率高到一定程度時，電機提供的轉矩在一個脈沖周期里不能使電機轉過一個步進角，此時電機將發生失步或堵轉，所以步進電機存在一個最大工作轉速。在步進電機速度發生突變時，若脈沖頻率變化不合理，電機提供的轉矩在一個脈沖周期里不能使電機轉過一個步進角或超過一個步進角，電機將會發生失步、堵轉或過沖，為此可以在步進電機變速時引入一個合理的加減速過程以解決這個問題。

常見的步進電機加減速控制方法主要有：直線型加減速曲線、指數型加減速曲線和S型加減速曲線。直線型加減速曲線在加速、勻速和減速過程中不能光滑過渡，主要適用于控制系統處理速度較慢且對升降速過程要求不高的場合；指數型加減速曲線的平滑性好，運動精度高，但在加減速的起點存在加減速突變；S型加減速曲線的加速度和速度曲線具有連續性特性，能夠保證步進電機在運動過程中速度和加速度沒有突變，減小沖擊，從而提高步進電機的平穩性[1-2]。課題組根據ARM的STM32F103ZET6芯片，提出一種基于七段加減速S曲線的改進S曲線加減速算法，將其用于步進電機的動態調速中，提高步進電機運行時的穩定性和可靠性。

1 步進電機加減速S曲線

步進電機加減速S曲線，指的不是某一特定的算法，而是對加減速曲線呈S型算法的統稱。常用的S型曲線主要有2種：一種是引入Sigmoid函數曲線作為加減速的速度曲線；另一種是在加減速階段引入加加速度來控制加速度，以防止加速度突變出現柔性沖擊而影響步進電機的平穩運行。

1.1 Sigmoid曲線

Sigmoid函數在生物學和信息工程學中是常見的函數。將Sigmoid函數圖像向右平移a個單位，可作步進電機加速段的速度S曲線圖，函數的表達式為式(1)，其導函數曲線可作步進電機S曲線的加速度曲線圖，函數表達式為式(2)。圖1所示的是a取5時Sigmoid曲線圖和其導函數曲線圖。

(1)

(2)

由圖1(b)Sigmoid導函數曲線圖可以看出，步進電機在加速階段，加速度沒有突變且沒有拐點，整條加速度曲線光滑。說明Sigmoid函數做加減速S曲線可使電機避免加速過程出現剛性沖擊和柔性沖擊，有利于電機的加減速過程的平穩工作。但是在Sigmoid函數里含有ex項，當計算機處理這類函數時要花費遠超加法和乘法運算的時間，故在STM32微控芯片上計算Sigmoid函數需要更長的時間。當芯片計算函數值的時間超過變頻的時間時，會導致加速曲線出現不可預測的變化，從而導致電機運行的不平穩。

1.2 引入加加速度的S曲線

引入加加速度的加減速S曲線一般可分為包含加加速段、減加速段、勻速段、加減速段和減減速段的5段加減速控制曲線，以及包含加加速段、勻加速段、減加速段、勻速段、加減速段、勻減速段和減減速段的7段加減速控曲線。常見的5段加減速曲線圖如圖2(a)所示；常見的7段加減速曲線圖如圖2(b)所示。

由圖2(a)的加速度曲線圖可以看出，在加、減速階段，加速度圖存在拐點，拐點的存在可能在運動中會引起柔性沖擊。7段加減速曲線是基于5段加減速曲線的改進，由圖2(b)和圖2(a)加速度曲線圖對比可知，在完成同樣的加速過程的情況下，若加速時間相同，7段加速曲線中的最大加速度會更小，運行更穩定；若最大加速度相同，7段加速曲線會用更短的時間完成加速過程，即7段加速度曲線能更好地兼顧效率和平穩性。但7段加減速曲線，在加速度曲線上仍舊存在拐點，而且分段區間增多，控制算法變復雜，會影響實時控制系統的運算效率[3]。

2 構造7段加減速S曲線并優化

課題組針對7段加減速S曲線加速階段中加速度存在拐點和加速階段分段區間多，影響實時控制系統運算效率的問題，提出一種基于多項式擬合S加減速曲線的方法，在保留7段加減速曲線的優異加減速性能的同時，消除7段加減速曲線中加速度存在的拐點，使加速段或減速段成為單一的函數曲線。因此，課題組采用了大于三次多項式擬合加減速階段的速度曲線。這樣既可以保證速度曲線和加速度曲線連續可導，又能避免電機在運行過程中出現柔性沖擊。

2.1 構造7段加減速S曲線

從圖2(b)可知，曲線圖上存在6個拐點，并以此為分界線。0～T1時間段內，速度由起始v0加速至拐點T1，加加速度a′為常數z，加速度a由0逐漸增加；T1～T2時間段，速度恒定增加，加速度為最大加速度amax；T2～T3時間段，速度減速增加，加加速度a′為常數-z，加速度a由amax逐漸減到0；T3～T4時間段,速度為恒速；T4～T5,T5～T6和T6～T7為減速段，與加速段類似，加速度變化為負值。

加速段S曲線方程如下：

1) 0～T1時間段內

加加速度為z(z>0)，加速度和速度方程分別為：

a=zt;

(3)

(4)

2)T1～T2時間段內

加速度為最大加速度，加速度和速度方程分別為：

a=amax;

(5)

(6)

3)T2～T3時間段內

加加速度為-z，加速度和速度方程分別為：

a=amax-z(t-T1);

(7)

(8)

4)T3～T4時間段內

速度為恒定值。

減速段T4～T5,T5～T6和T6～T7與加速段一致，可看作加速段的逆過程[4]。

2.2 優化7段加減速S曲線

對構造出的加速S曲線在隔開拐點處均勻取點，該取點方式可以更好地優化拐點處的函數曲線，采集的點集用數組的方式表示，記作pi(xi,yi)。對采集的數據點用多次多項式擬合，即對采集的數據點集做線性回歸處理。

2.2.1構造優化模型

對擬合的近似曲線進行假設，其假設的線性回歸模型的函數表達式為

(9)

式中：hθ(x)表示擬合曲線的函數值，θj表示函數多項式系數。

采用均方誤差(MSE)作為線性回歸模型的損失函數。損失函數的表達式為

(10)

式中：J(θ0，…，θn)表示均方誤差，hθ(xi)表示在點xi處擬合曲線的函數值。

損失函數式(10)表示線性回歸模型(擬合曲線上)的點與采集數據點偏差值的平方和，可用來描述線性回歸模型與數據點集之間的差異。如果損失函數J(θ0，…，θn)=0，表示完全沒有差異，則說明此線性回歸模型完全描述數據之前的關系。如果需要找到最佳擬合的線性回歸模型，就需要使對應的損失函數最小;求解最小損失函數的參數組，得到擬合曲線的函數表達式。

2.2.2求解最小損失函數

計算最小損失函數有2種實現方式：①梯度下降求損失函數最小值；②正規方程求解損失函數最小值。

2.2.2.1梯度下降原理

當選擇梯度下降計算損失函數最小值時，開始隨機選擇一個參數的組合(θ0，θ1,…，θn)，計算損失函數;然后尋找下一個能讓損失函數下降最多的參數組合，將該過程迭代，直到損失函數收斂到一個局部最小值。批量梯度下降的算法公式為

(11)

式中：“:=”是賦值符號，表示對左邊變量進行賦值；β表示損失函數每次沿下降方向下降的程度。

2.2.2.2正規方程

求解損失函數最小值，即損失函數極值問題。對損失函數的參數(θ0，θ1,…，θn)求偏導數，令其為零，即可得到滿足條件的參數組(θ0，θ1,…，θn):

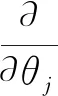
(12)

采用單個方程逐一求解參數組中各參數的值，其求解的效率很低，因此可以采用矩陣的方式進行求解。用列向量θ表示損失函數的參數組(θ0，θ1,…，θn)，用m行n+1列的矩陣X表示m組n+1維的特征向量。用列向量Y表示(y1,y2,…,ym);列向量HθX表示(hθ(x1),hθ(x2),…,hθ(xm));J(θ)表示損失函數的值。擬合曲線的線性回歸模型用矩陣可表示為

HθX=Xθ。

(13)

損失函數矩陣為

(14)

式(14)展開為

(15)

對各參數求偏導,得到

(16)

化簡為

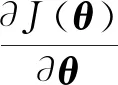
(17)

θ=(XTX)-1XTY。

(18)

式(18)為正規方程的表達式。

3 具體算法的實現

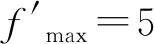
由于擬合曲線采用6次多項式，即擬合曲線只有7項特征，梯度下降和正規方程都能很快求解出損失函數最小值的參數，但相較而言梯度下降更擅長求解多特征的函數(特征值大于10 000)，正規方程更適合求特征值較少的函數。用MATLAB計算正規方程求解得到θ參數的組：

θ0=86.339 127；θ1=245.822 054；θ2=508.687 301；θ3=0.573 600；θ4=-3.256 022；θ5=0.197 272；θ6=-0.003 721。

擬合曲線的方程為

(19)

截取0～22.4 s內的頻率導數擬合曲線，如圖4所示。

4 動態調速

在實際運行過程中，頻率的變化是離散的，需要對曲線離散取值。課題組采用等時間間隔數值的階梯逼近升速S曲線取值，等脈沖數為階梯實際維持長度的方案，示意圖如圖5所示[6-9]。

對于階梯的維持時間的長度有等時長和等脈沖數2種方案。

1) 等時長方案。每個階梯維持相同的時間，它能很好地反映S曲線的特性，但是第1個階梯的脈沖數和最后1個階梯的脈沖數相差很大。步進電機在調速時，步進電機的轉子轉過第1個步進角停下的位置時，轉子會出現一定程度的震蕩。為解決該震蕩，需要增加幾個同頻脈沖使轉子運行平穩，但同頻脈沖過多并不會繼續提高其平穩性。

2) 等脈沖數方案。每個階梯維持相同的脈沖數。在選取了合適的同頻脈沖數后，能對S曲線的性能進一步優化，提高運行的效率。

選取同頻等脈沖數作為階梯維持時間，能在保持近乎相同的性能下，提高運行效率。經試驗測得，5作為同頻脈沖數是一個較合適的值[10]。

取圖5中S曲線與階梯的接觸點為離散的取值點，記為(tk,fk)。k表示S曲線上取的第k個點，fk表示第k個點運行的頻率，tk表示第k個點時間的數值。圖5中Δt表示等時間間隔數值,Δtk表示以(tk,fk)為起點的實際階梯時間維持長度，即圖中第k個灰柱條的寬度。

第k個階梯實際的維持時間為

Δtk=w·tplusek。

(20)

在tk點的實際運行時間為

(21)

式中：tplusek表示第k個點單個脈沖持續的時間；tplusem表示第m個點單個脈沖持續的時間;w表示同一頻率脈沖的個數。

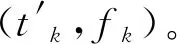
在動態調速過程中，脈沖頻率(速度)增加的數值可以是0～90 000 Hz之間的任意值，所以不可能為每一個調速建立一個S曲線。為了實現范圍調速，可以先建立一個通用的S曲線模型，然后對其進行拉伸、壓縮以對應不同的調速。拉伸和壓縮后的曲線仍會保留大部分原曲線特性。

通過給S曲線函數乘以一個系數ε得到需要的增速，即在縱軸上對實際S曲線進行壓縮[11]。針對不同的增速，可選取相對應的等時間間隔數值Δt和同頻脈沖數，保證動態調速的效率和穩定性。經多次試驗表明，此方法有良好的動態調速性能。

經過試驗發現，可以先獲得某一同頻脈沖數下步進電機不發生堵轉的初速度、增速和等時間間隔數值Δt的臨界關系表。然后取臨界等時間間隔數值Δt′的1/4為穩定等時間間隔數值Δt″，可得到初速度、增速和等時間間隔數值Δt穩定關系表。

將初速度、增速和等時間間隔數值Δt穩定關系圖表作為動態選擇等時間間隔數值Δt的依據，協同優化后的S曲線算法寫入內存，即可作為動態調速控制的核心，實現對步進電機進行平穩的動態調速。

5 結語

課題組通過優化七段加減速S曲線，在保留其優良特性的同時，消除加速度曲線存在的拐點，并將加或減速過程中的3段函數用1段函數替代，降低算法的復雜性，同時精簡了代碼。基于優化后的S曲線，采用等時間間隔數值的階梯逼近升速S曲線取值，等脈沖數為階梯實際維持長度的方案用于實際控制步進電機。經試驗得到初速度、增速和等時間間隔數值Δt使電機平穩運行的關系。試驗表明，采用本研究所述方法，步進電機在指定的范圍內能進行平穩的動態調速。