同軸結構球形液滴的尺寸效應和電場動力學
馬 鶴,陳思博,吳金兵,周 璇,張志東*
(1.河北工業大學 應用物理系,天津 300401;2.河北工業大學 電子信息工程學院,天津 300401;3.天津市材料器件重點實驗室,天津 300401)
1 引 言
聚合物分散液晶(Polymer Dispersed Liquid Crystal,PDLC)廣泛應用于許多電光器件中,如智能窗、光學開關、生物傳感器和微激光器[1]等。PDLC由分散在光學透明聚合物薄膜中的向列相液晶球形微滴組成。液晶球形微滴中液晶分子排布通常有如下幾種構型:雙極(Bipolar)結構、扭曲雙極(Twisted bipolar)結構、同軸(Concentric)結構、徑向(Radial)結構、軸向(Axial)結構、逃離徑向(Escaped radial)結構以及扭曲徑向(Twisting of the radial)結構。影響液晶分子排布的因素主要有邊界條件、彈性常數比值、微滴尺寸以及外場作用等[2]。液晶在球形有限幾何限定條件下的排布方式已經得到了學術界的廣泛關注[3-7]。例如:球形液滴表面邊界條件由沿面邊界條件(表面錨定方向垂直于徑向方向)改變為垂面邊界條件(表面錨定方向沿徑向)時,內部結構由雙極結構(Bipolar)變為徑向結構(Raidal)[3];在保持k24(Frank理論中的鞍形彈性常數)不變時減小微滴半徑,雙極(Bipolar)結構演變為徑向(Radial)結構[4]。該結果表明隨著半徑減小,表面能作用相對增強,k24項在彈性能、體能、表面能的相互競爭中逐漸占據優勢,促使液晶分子內部結構發生變化。當k22(Frank理論中的扭曲彈性常數)很小時,出現扭曲雙極(Twisted bipolar)結構[6]。
當液滴表面為垂面邊界條件時,液滴通常具有徑向結構和軸向結構,這些構型已被深入研究[8],本文不再進一步討論。對于沿面邊界條件,常見的結構為雙極結構和同軸結構。雙極結構同時具有展曲和彎曲形變,并且在k33/k11>1(k11、k22、k33分別為Frank理論中的展曲、扭曲、彎曲彈性常數)的液晶微滴中實現[9]。同軸結構中只存在彎曲形變,沿球心的直徑位置存在一條線缺陷,該結構在k33/k11<1的范圍內可存在。由于大多數向列相液晶材料滿足k33/k11>1,同軸結構通常很難在實驗中觀察到。Drzaic[10]發現了k33/k11<1的液晶材料, 并且該材料的彈性常數也符合扭曲雙極結構出現的判據k11>k22+0.431k33[11],所以該材料形成的液晶微滴易出現扭曲雙極結構,而不是同軸結構;在具有極小彎曲彈性常數k33的溶致液晶微滴中,可觀察到具有純彎曲變形的同軸結構,其中心軸處存在一條線缺陷[6]。然而,之前已有大量的理論研究表明:由于缺乏具有小彎曲彈性常數k33的熱致液晶,在熱致液晶系統中很少能觀察到同軸結構[6,11]。最近,楊登科[12]等人通過添加CB7CB減少液晶材料k33和k11的比值至0.632,實現了從雙極結構到穩定同軸結構的轉變。在熱致液晶中實現同軸結構,激發了我們對該結構進行理論研究的興趣。
PDLC(通常具有雙極結構)在沒有外加電場的情況下,由于各向異性的液晶微滴與聚合物網絡的折射率不均勻,光在通過系統時會發生散射,所以不透光。當在薄膜上施加電場時,液晶微滴中雙極軸重新排列,系統可透光。PDLC薄膜在外電場影響下的光學特性以及液晶微滴在外場存在時雙極軸重新排列的動力學過程已經得到了很好的解釋[13-14]。同時,在電場作用下,液滴內部也會存在結構重新排列的現象[15],本文主要探究電場作用下同軸結構微滴內部結構重新排列的動力學過程。液晶分子重新排列發生在幾微秒到十分之一秒的大范圍時間尺度內。這些研究中的動力學復雜性歸因于液滴大小和形狀,以及液滴內指向矢重新排列前后的差異。
本文基于Landau-de Gennes理論,研究半徑、電場對同軸結構液晶微滴的影響,采用與液滴中心軸平行的電場方向,主要研究電場作用下結構轉變的動力學過程。
2 幾何模型
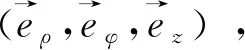
在球形液滴中,液晶分子的排布具有軸對稱性,即與φ無關,所以我們可以用半球的截面來描述整個球體的結構,此時液滴中過球心的中心對稱軸與坐標系的z軸重合。球形液滴表面采用沿面各向同性弱錨定邊界條件,中心軸采用自由邊界條件。
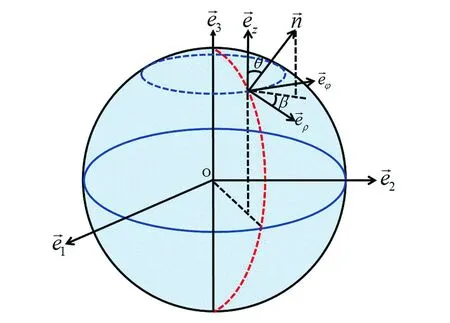
圖1 球狀結構示意圖Fig.1 Schematic diagram of spherical structure
3 理論方法
相較于Frank理論,Landau-de Gennes理論對向列相液晶系統中線缺陷和表面缺陷的描述更為精確,因此本文使用Landau-de Gennes理論進行研究。根據Landau-de Gennes理論,序參數張量Q可以表示液晶系統中分子在空間的有序程度。序參數張量Q[16]在主軸系中可以表示為:
(1)
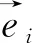
Q是對稱無跡張量,滿足Qij=Qji,trQ=0。系統處于各向同性相時,Q為零張量。系統處于單軸態時,Q的3個本征值中有兩個相等,另一個本征值對應的本征矢為指向矢,此時Q可以寫為:
(2)
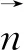
(3)
由于Q具有對稱性和無跡性,所以Qρφ=Qφρ,Qρz=Qzρ,Qφz=Qzφ,Qρρ+Qφφ+Qzz=0。系統處于雙軸態時,Q,3個本征值各不相同,雙軸性參數β2確定雙軸性大小:
(4)
雙軸性參數β2反映了三維空間中Q的不均勻性,其取值范圍為[0,1]。當β2=0時,系統處于單軸態,當β2=1時,系統處于最大雙軸態。在本征坐標系中,存在tr(Q3)=3detQ,聯系式(4),發現當detQ=0時,即3個本征值中至少有一個為0時,得到β2=1。
在有外加電場的液晶系統中Landau-de Gennes理論的總自由能表示為:
(5)
其中:液晶微滴的體積為V,Fbulk為本體自由能密度,Fbulk只依賴于序參數張量,不依賴于其空間變化率,其具體表達式為:
(6)
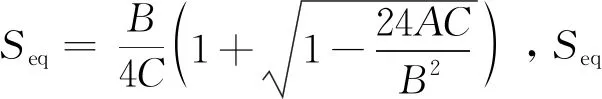
Felastic為液晶取向序的不均勻引起的彈性自由能密度,依賴于序參數張量Q的空間變化率,僅考慮Q及其導數的二次項,Felastic具體表示為:

(7)
Li與Frank理論中的展曲彈性常數k11、扭曲彈性常數k22、彎曲彈性常數k33之間存在關系為[17]:
(8)
電場引起的自由能密度表示為:
(9)
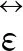
(10)
其中:εi=(ε‖+2ε⊥)/3為平均介電常數,εa=(ε‖-ε⊥)/Seq表示平均各向異性。本文選用正性液晶材料進行模擬計算,即εa>0,此時,正性液晶分子趨于與電場E平行的方向有序排列。本文只考慮介電作用,Fdielectric可以表示為:
(11)
柱坐標系下各向同性弱錨定表面自由能密度表達式為:
(12)

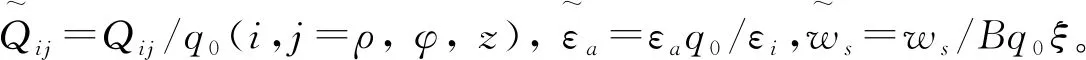
(13)
(14)
(15)
(16)
利用張量Q無跡處理和泛函的約束變分得到該體系約化后的歐拉方程[20]。在柱坐標系為
(17)
使用松弛迭代方法對液晶系統進行數值模擬,利用動力學方程,讓序參數張量Q在一定的初始狀態下隨時間演化,得到其平衡態結果。
動力學方程如下:
(18)
其中:Γ=6D*/[1-3tr(Q2)]2,D*是向列相的轉動擴散系數。約化后的動力學方程為:
(19)
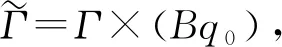
(20)
弱錨泊的邊界條件方程為:
(21)
上式約化得到的方程為:
(22)
對于球形液滴可以表示為:
(23)
本文模擬過程中體系數選取了液晶材料5CB[16]的各項系數為:A0=0.195×106J/m3,B=7.155×106J/m3,C=8.82×106J/m3,D*=0.35 m2N-1s-1,彈性系數選取楊登科[12]實驗中彈性系數k11=9.5×10-12N,k22=8×10-12N,k33=6×10-12N,對應到Landau-de Gennes理論中可以得到L1=33.387 5×10-12N,L2=14.657 9×10-12N,L4=-53.457 7×10-12N,對應的相干長度ξ約為4.8 nm,約化溫度設定為則序參數約化后為介電各向異性Δε=6.4(ε⊥=5.4)。計算可得電場約化參數為E0=33.7 V/μm。設定錨定強度系數w=10-4J/m2,約化后的錨定強度為
4 結果與討論
4.1 同軸結構球形液滴
在沿面錨定以及單一彈性常數近似(k11=k22=k33)作用下,球形液滴通常為雙極結構。楊登科[12]等人通過改變彈性常數比值,即減小k33/k11比值至0.632,出現穩定同軸結構。取半徑為3 333ξ(約16 μm),且彈性常數和邊界錨定符合k33/k11=0.632的球形液滴進行模擬,得到該同軸結構的精細結構,指向矢示意圖如圖2(a)、(b)、(c)所示。

(a)三維同軸結構示意圖(a)Concentric configuration in 3D representation
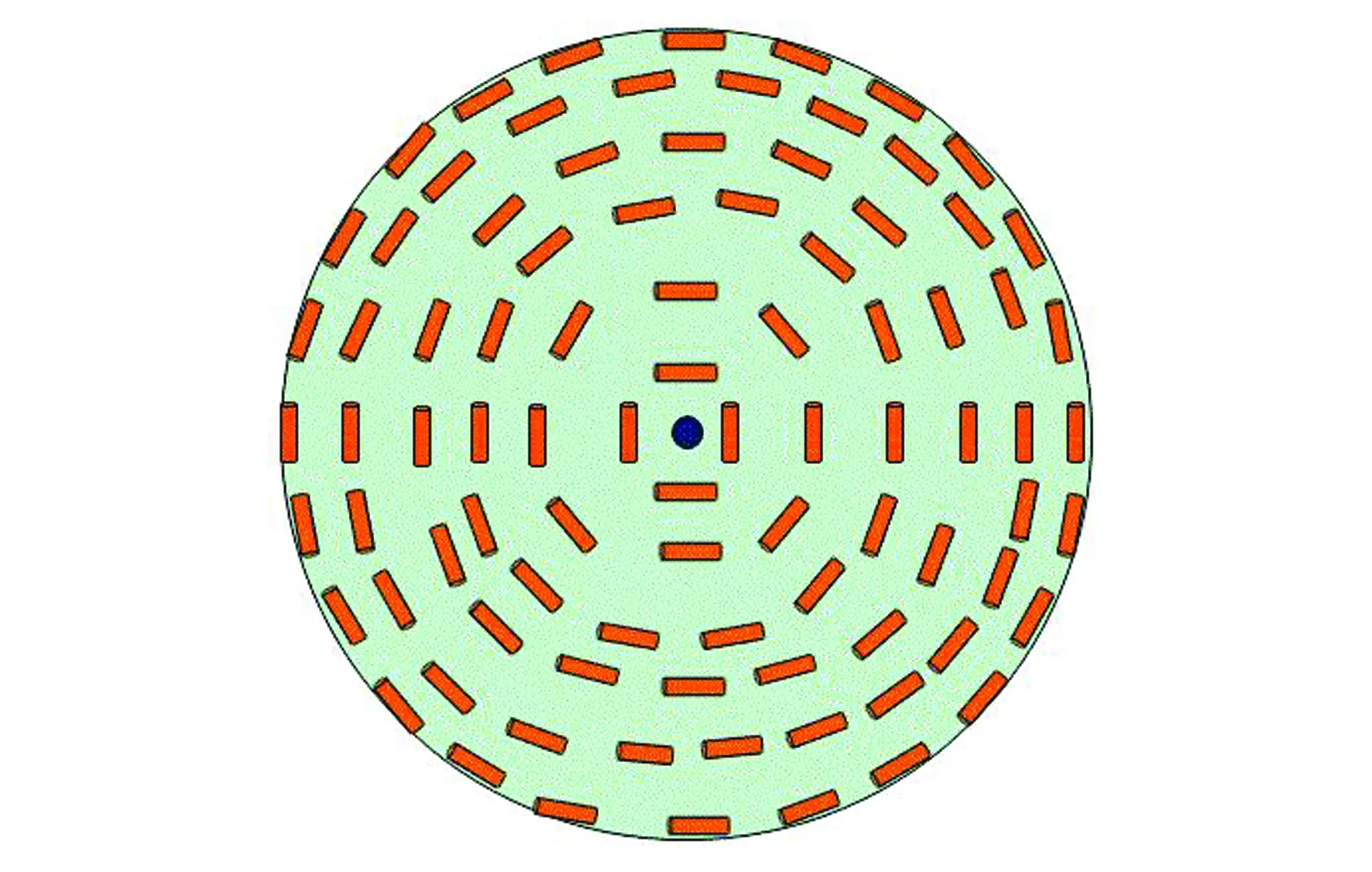
(b)赤道面截面圖(b)Cross section diagram of the equatorial plane
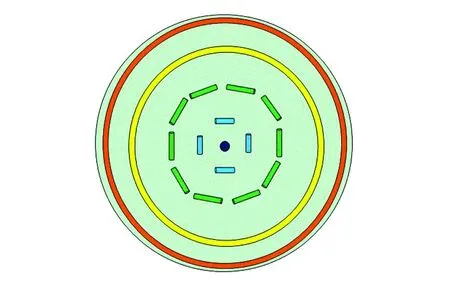
(c)距離兩極1/4位置截面圖(c)Cross section diagram of the position 1/4 away from the two poles
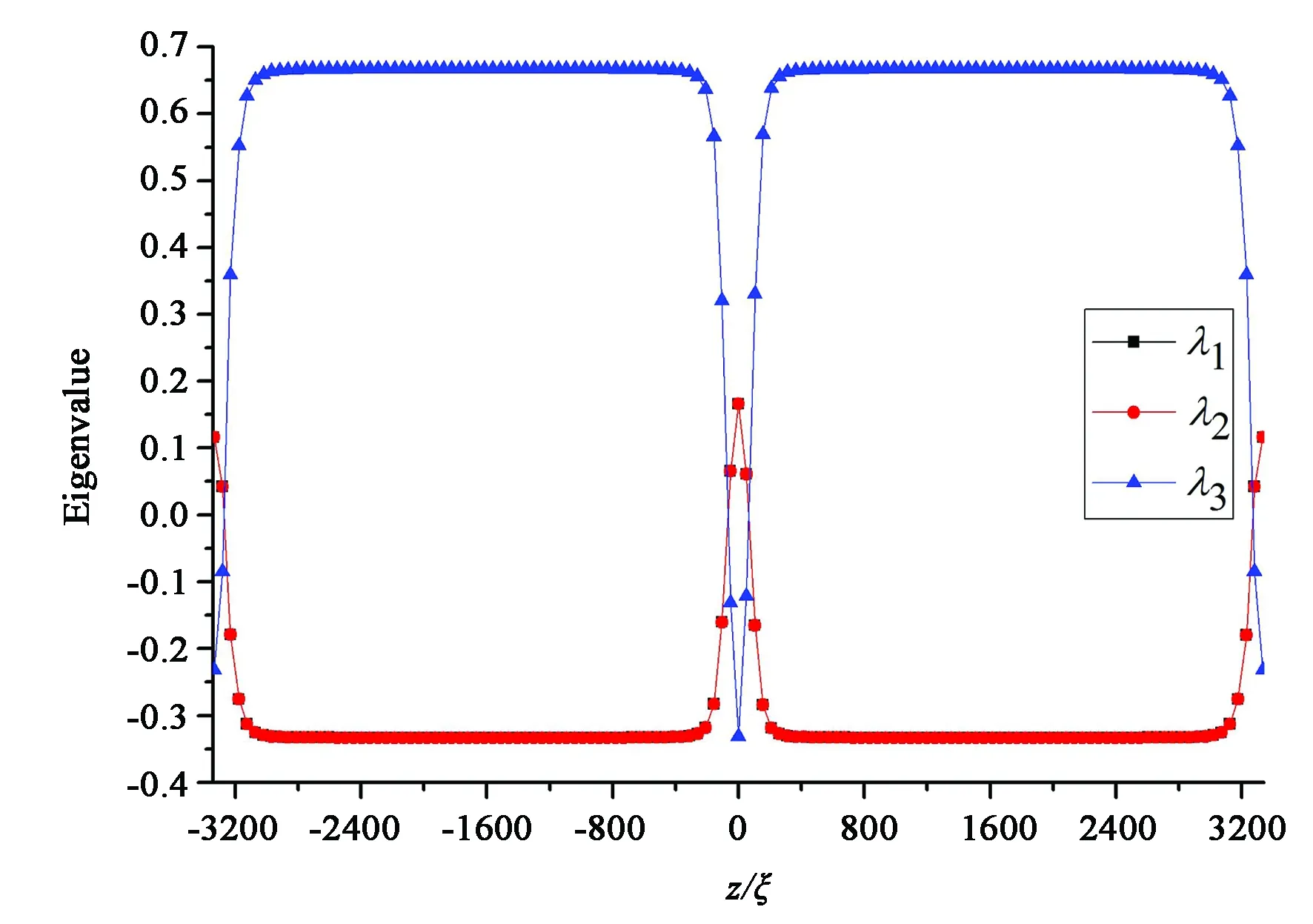
(d)中心軸處本征值(d)Eigenvalues at the center axis
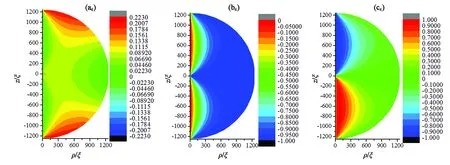
圖2中心軸處指向矢沿z方向排列,以赤道面分為對稱的上下兩部分,指向矢主要分布在φ-z平面內,在上下兩部分內,隨著位置ρ增加,指向矢出現φ分量且該分量逐漸增大。值得注意的是,指向矢從沿z方向轉動到沿φ方向的轉動過渡區域較小,該結構外部指向矢均沿φ方向排列。在赤道面上,除中心核處指向矢沿z方向,其余部分指向矢沿φ方向排列。該結構赤道面截面圖與楊登科[12]等人得到的俯視圖相同,如圖2(b)所示。圖2(c)為距離兩極頂點1/4位置的截面圖,隨位置ρ增加,指向矢z方向分量減小,外部指向矢沿φ方向。圖2(d)表示沿中心軸z方向指向矢的3個本征值分布圖,中心軸全部處于單軸態,在兩端點和中心核處本征值λ1=λ2,λ3<0,且根據指向矢情況可判斷在上下兩頂點與中心核處分別存在缺陷:兩端各存在一個彎曲點缺陷,中心核存在線缺陷。圖3(a)、(b)、(c)分別為指向矢在ρ、φ、z三個方向分量等高圖。
圖3(a)顯示該結構指向矢并非全部分布在φ-z面內,其在球中心核附近具有微小ρ分量。從圖3(a)可以看出沿z=0上下半圓中數據正負相反,顯示液滴沿著赤道面上下半球的手性相反,所以,一定存在同樣條件下的另一種異手性結構如圖4所示。圖3、4所示的兩種結構沿赤道面上下手性正好相反。
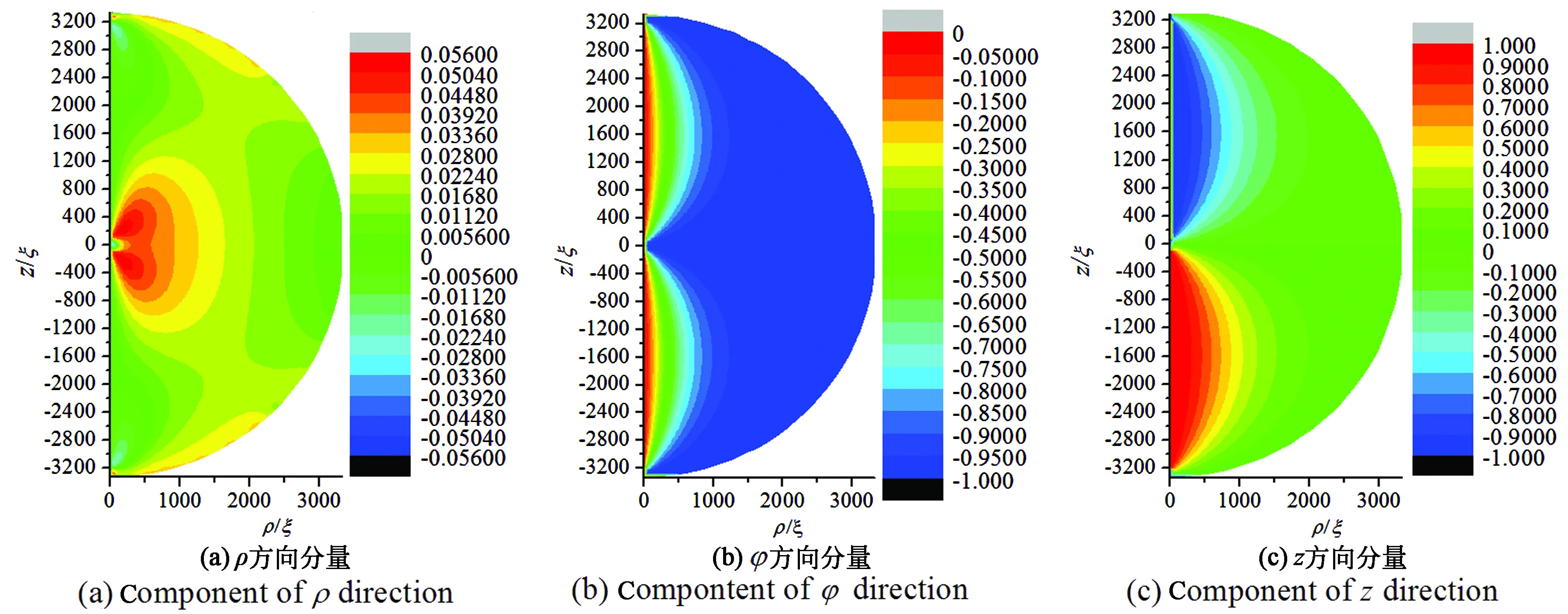
圖3 半徑為3 333ξ時同軸結構指向矢在ρ、φ、z三個方向分量等高圖。Fig.3 Contour diagram of axial structure pointing vector in ρ,φ,z directions with the radius of 3 333ξ.
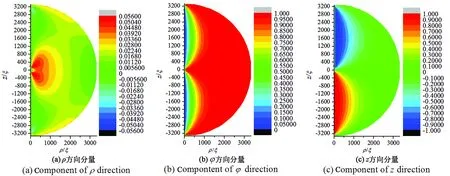
圖4 與圖3結構手性相反的同軸結構的指向矢在ρ、φ、z三個方向分量等高圖。Fig.4 Concentric configuration which is opposite to the chirality of the structure in Fig.3 points to the contour diagram of components in the directions of ρ,φ,z.
4.2 尺寸效應
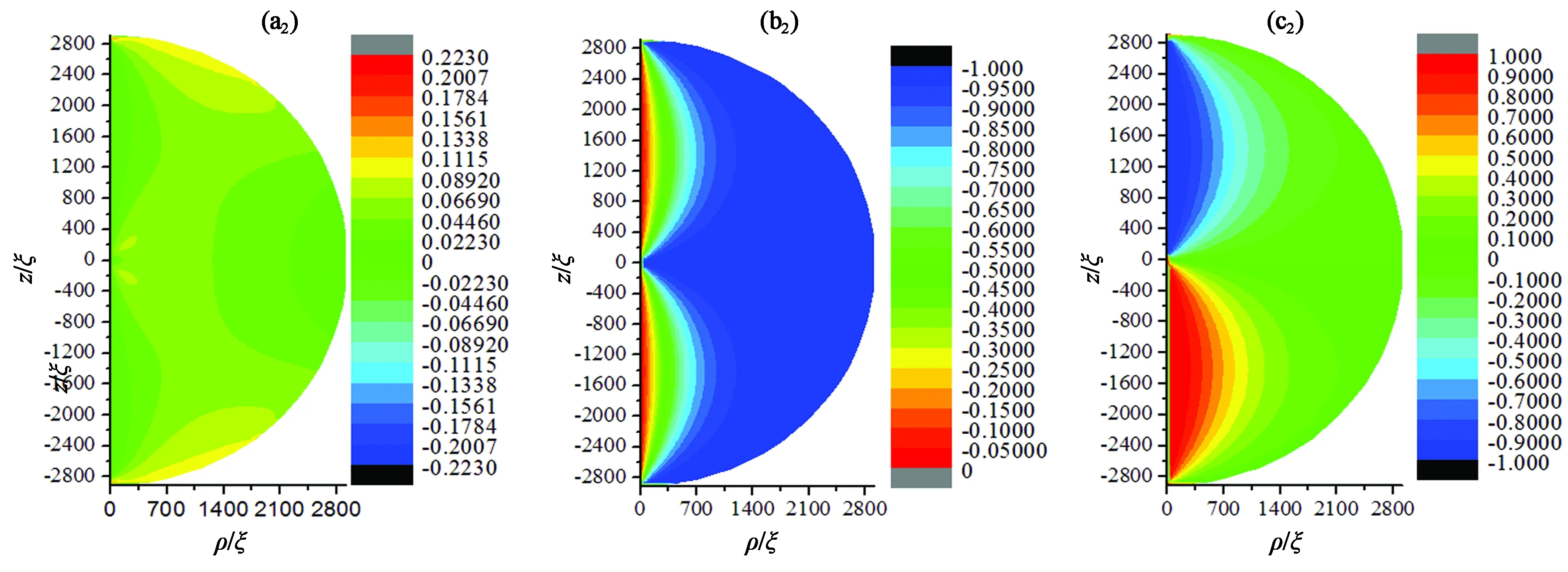
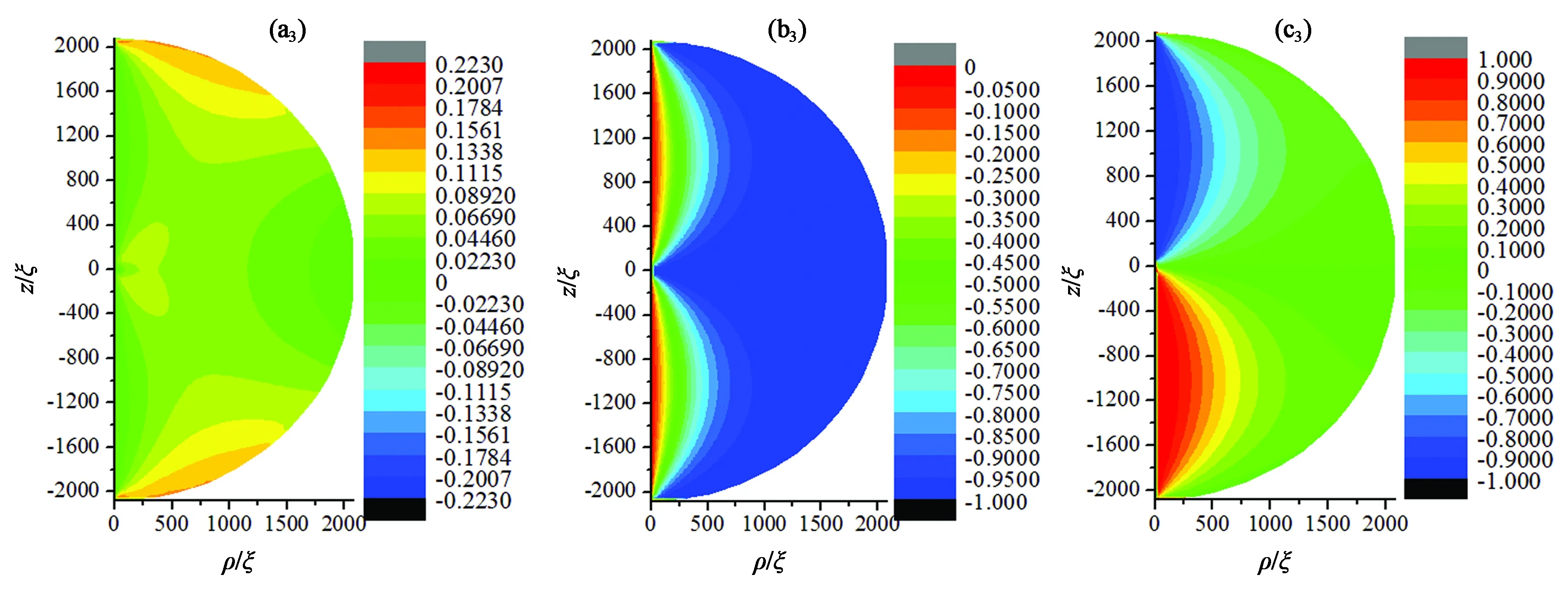
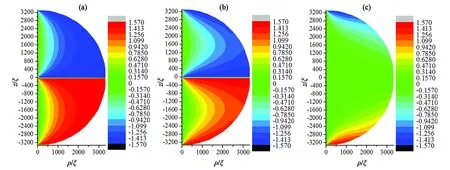
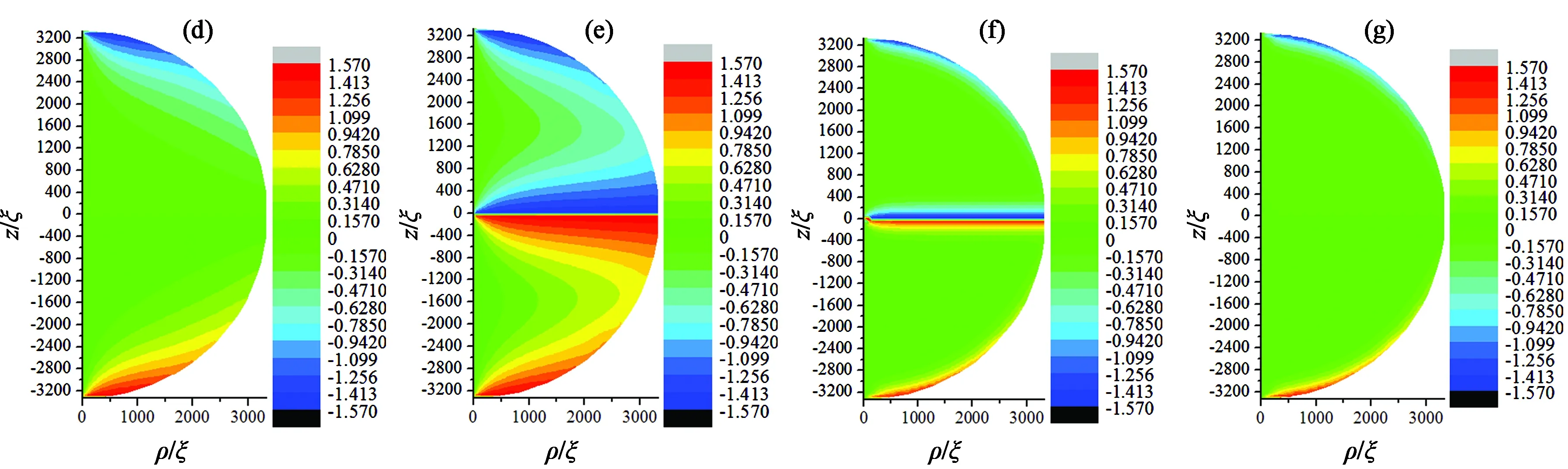
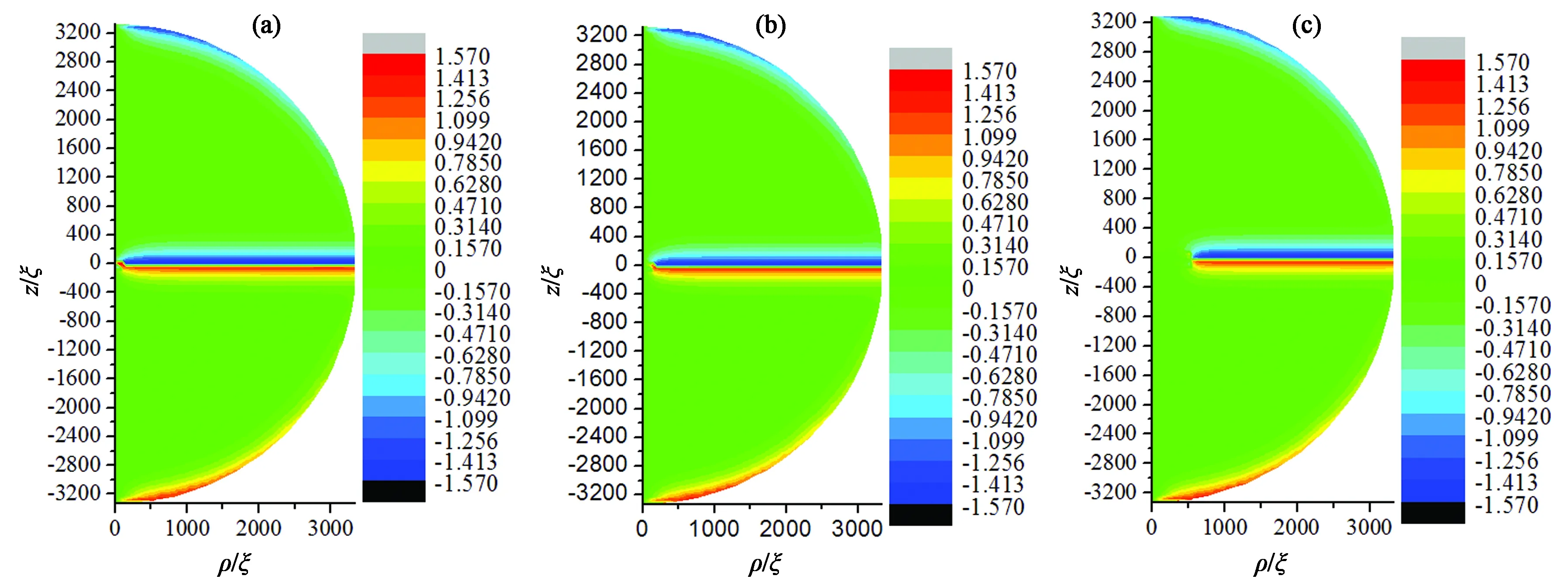
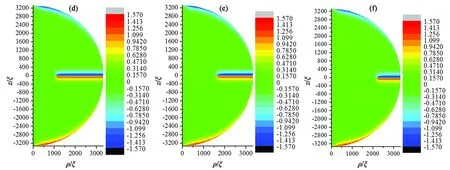
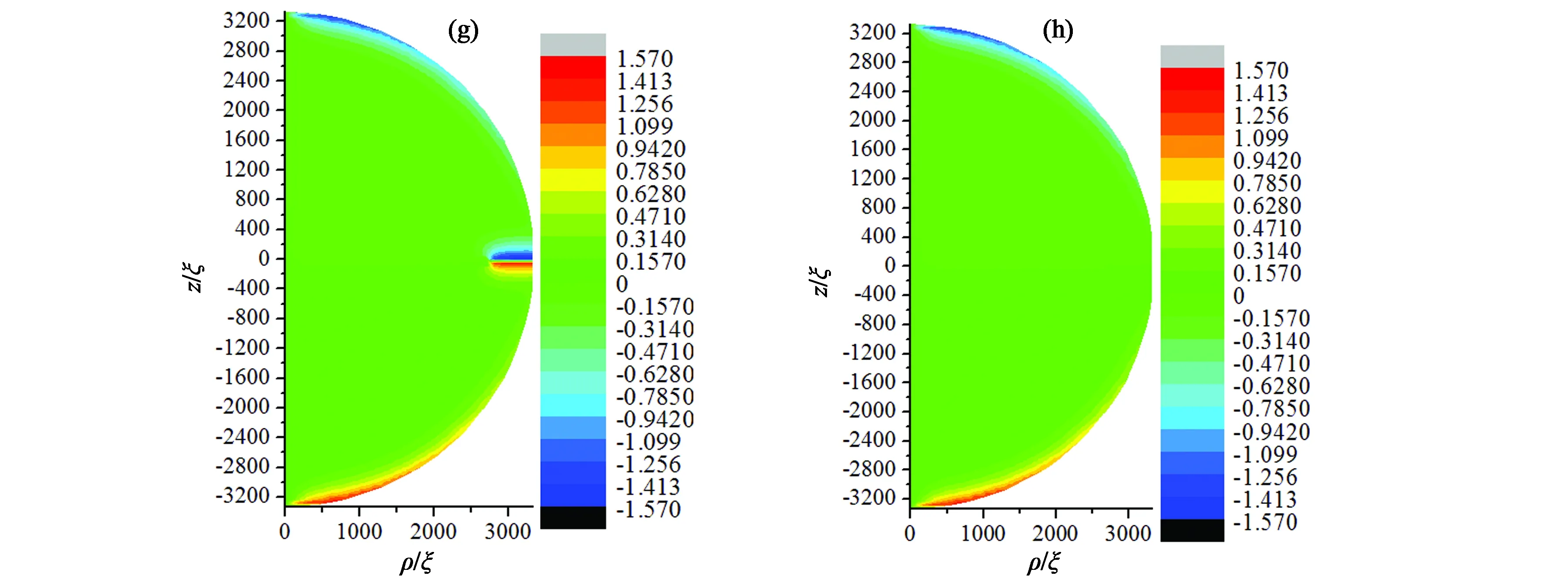
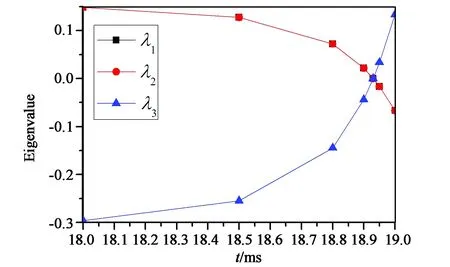
在彈性常數(k33/k11=0.632)和邊界條件(各向同性弱錨定)不變的情況下,選取半徑為3 333ξ(約16 μm)、2 917ξ(約14 μm)、2 083ξ(約10 μm)、1 250ξ(約6 μm)、1 083ξ(約5.2 μm)、1 042ξ(約5 μm)、208ξ(約1 μm)的球形液滴,觀察半徑誘導的結構變化。如圖5所示,半徑分別為3 333ξ[(a1), (b1), (c1)]、2 917ξ[(a2), (b2), (c2)]、2 083ξ[(a3), (b3), (c3)]、1 250ξ[(a4), (b4), (c4)]時球形液滴內部結構的三分量等高圖。當1 083ξ 通過二分法可得系統結構、能量與尺寸的關系如表1所示。r≤1 063ξ(約5.1 μm)時,雙極結構穩定存在;1 083ξ(5.2 μm)≤r<1 354ξ(6.5 μm),同軸結構和雙極結構能量相同,二者為雙穩態;r≥1 354ξ(6.5 μm),同軸結構穩定存在。 圖5 半徑分別為3 333ξ,2 917ξ,2 083ξ,1 250ξ指向矢在3個方向分量等高圖。(a1) ,(b1) ,(c1) r/ξ = 3 333;(a2), (b2), (c2) r/ξ = 2 917;(a3),(b3), (c3) r/ξ =2 083;(a4), (b4), (c4) r/ξ = 1 250。Fig.5 Contour maps of pointing vectors in three directions with radiis of 3 333ξ, 2 917ξ, 2 083ξ and 1 250ξ, respectively. (a1) ,(b1) ,(c1) r/ξ=3 333; (a2), (b2), (c2)r/ξ= 2 917,(a3),(b3), (c3) r/ξ=2 083; (a4), (b4), (c4)r/ξ= 1 250. 表1 結構、能量與尺寸的關系Tab.1 Relationship among structures, energy and radius 4.3.1 半徑為3 333ξ(16 μm)時電場誘導的結構轉變 選取半徑為3 333ξ(約16 μm)的穩定同軸結構球形液滴,施加沿z方向電場,探究外電場對系統結構的影響。當系統存在電場影響時,此時液滴內電場能、彈性能、表面能相互競爭,通過記錄不同電場下極角θ變化,探究液晶系統的兩次結構轉變過程。首先為第一次結構轉變。如圖6(a)、(b)所示,當0≤E/E0≤0.002 4,隨著電場強度增大,微滴以赤道面為對稱面上下對稱的兩部分內極角為0的區域向邊界擴大,即沿中心軸方向排列的液晶分子范圍擴大。繼續增大電場,如圖6(c)、(d)所示,第一次結構轉變出現。當0.002 7≤E/E0≤0.003時,3種能量達到一種特殊的平衡而出現類似于雙極結構的構型。此時,逐漸增強的電場能使更多液晶分子沿z軸排列,但是邊界表面仍能對液滴結構產生影響,所以在液滴上下兩極附近液晶分子仍沿φ方向排列,其余部分沿z方向排列。如圖6(e)、(f)所示,當0.003 3≤E/E0<0.013 4時,上述特殊平衡被打破,電場能逐漸占據主導位置。球體上下對稱部分指向矢沿中心軸方向,赤道面附近指向矢沿φ方向。電場強度越大,赤道面附近指向矢沿φ方向區域越小,上下兩極附近的液晶分子在ρ-z面內沿球面排列。電場強度由E/E0=0.013 4增加到E/E0=0.013 5時,第二次結構轉變完成,出現如圖6(g)所示結構,由于錨定作用的存在,邊界處指向矢沿面排列,其余部分指向矢沿中心軸方向排列,該結構與圖6(c)、(d)中所示結構相似,不同之處在于該結構指向矢只分布在ρ-z平面內,而圖6(c)和圖6(d)所示結構中,兩極附近指向矢沿φ方向扭曲。下面探究第二次結構轉變的詳細過程。 圖6 給半徑為3 333ξ (約16 μm)的同軸結構施加不同電場時,其指向矢對應的極角示意圖。(a) E/E0=0;(b) E/E0=0.002 4;(c) E/E0=0.002 7;(d) E/E0=0.003;(e) E/E0= 0.003 3;(f) E/E0= 0.013 4;(g) E/E0= 0.013 5。Fig.6 Polar angle on the ρ-z plane for different E/E0 values applied in concentric structure with d=3 333ξ (about 16 μm). (a) E/E0=0; (b) E/E0=0.002 4; (c) E/E0=0.002 7; (d) E/E0=0.003; (e) E/E0=0.003 3; (f) E/E0=0.013 4; (g) E/E0=0.013 5. 4.3.2 場致結構轉變動力學過程 定義Ec/E0=0.013 4為系統出現新型結構轉變的閾值電場。下面探究在該電場下系統從Ec/E0= 0.013 4增加到E/E0=0.013 5時的結構轉變動力學過程。圖7所示為在電場E/E0=0.013 5下球內液晶分子指向矢對應的極角圖,該圖顯示,隨著所加電場時間增加,球內赤道面附近液晶分子指向矢從中心軸到邊界逐點由φ方向轉變為電場方向z,該現象在以往研究中從未出現。 圖7 電場為E/E0=0.0135時,系統發生最后一次結構轉變的動力學過程。(a) t=10 ms;(b) t=20 ms;(c) t=30 ms;(d) t=40 ms;(e) t=50 ms;(f) t=60 ms;(g) t=70 ms;(h) t=80 ms。Fig.7 Dynamical process of the last structural transformation with E/E0 = 0.013 5. (a) t=10 ms; (b) t=20 ms; (c) t=30 ms; (d) t=40 ms; (e) t=50 ms; (f) t=60 ms; (g) t=70 ms; (h) t=80 ms. 如圖8所示,λ1、λ2、λ3分別為序參數張量Q的3個本征值。當t=0 ms時,中心核(0, 0)處λ1(黑色點線)=λ2(紅色點線),λ3(藍色點線)<0,該點處于沿z方向的負序參數單軸態。施加沿z方向的電場,λ1和λ2減小,λ3增大。當t=18.9 ms時,λ1=λ2=λ3中心核處變為各向同性點。隨著時間增加,λ1、λ2、λ3保持原變化趨勢,中心核處逐漸演變為沿z方向的正序參數單軸態。同時赤道面附近液晶分子指向矢沿著z軸電場方向轉動。通過選取赤道面上特定點(781ξ,0)的指向矢轉動情況,可了解赤道面附近液晶分子指向矢轉動的詳細過程。如圖9所示,當t≤32 ms時,(781ξ,0)處指向矢z方向分量為0,即該處液晶分子與電場方向垂直,沿φ方向排列。當t>32 ms時該點指向矢由于對稱性破缺,由φ方向逐漸向z方向轉動。當電場持續時間為t=40 ms時,液滴內(781ξ,0)處指向矢z方向分量基本為1,此時液晶分子沿電場方向排列。隨著施加電場時間增加,沿z方向排列的液晶分子指向矢區域逐漸向邊界擴大。 圖8 電場為E/E0=0.013 5時,中心核處本征值變化曲線。Fig.8 Profile of eigenvalue in the center for E/E0=0.013 5 圖9 電場E/E0=0.013 5時,(781ξ,0)處指向矢動力學過程。Fig.9 Dynamical process of director at the intersection point of (781ξ,0) with E/E0=0.013 5 本文基于Landau-de Gennes理論,利用松弛迭代方法,研究了穩定同軸結構液晶微滴的兩種精細結構。該結構中心軸處指向矢沿z方向;球體上下兩部分內部液晶分子指向矢從中心軸到邊界處,由z方向轉到φ方向;赤道面上中心核處指向矢沿z軸排列,其余部分指向矢沿φ排列;該結構兩極和中心核處存在缺陷。首先探究了無電場條件下,液晶微滴的尺寸效應。當液晶微滴半徑范圍為5.2 μm ≤r≤16 μm時,同軸結構穩定存在;隨著半徑減小,尺寸效應逐漸明顯,φ、z方向分量稍微減小,ρ方向分量稍微增大。其中當5.2 μm≤r≤6.5 μm時,同軸結構和雙極結構同時存在,為雙穩態。當r≤5.1 μm時同軸結構不穩定,出現雙極結構。 當存在沿z軸方向外電場時,隨著施加的電場強度增加,出現兩次結構轉變。當0≤E/E0≤0.002 4時,沿中心軸方向排列的液晶分子范圍擴大,當0.002 7≤E/E0≤0.003時,體能、彈性能、表面能達到某種特殊平衡,液晶微滴形成類似雙極結構的構型,此時為第一次結構轉變;當0.003 3≤E/E0<0.013 4時,上述特殊平衡被打破,球體上下對稱部分指向矢沿中心軸方向,赤道面附近指向矢沿φ方向,且電場越大,沿中心軸方向的指向矢區域越大。當電場強度達到閾值電場E/E0=0.013 4時,第二次結構轉變出現,出現動力學過程而使系統大部分液晶分子沿z方向排列。重點探究閾值電場E/E0=0.013 4下第二次結構轉變的動力學過程,我們首次在同軸結構內發現:中心核處由沿z方向的負序參數單軸態演變為各向同性態,再演變為沿z方向的正序參數單軸態。中心核處態的改變誘導赤道面液晶分子指向矢通過對稱性破缺實現了動力學過程:從中心軸到邊界逐點向z方向轉動,最終達到單軸態。電場作用下,另一種異手性同軸結構也有對應現象。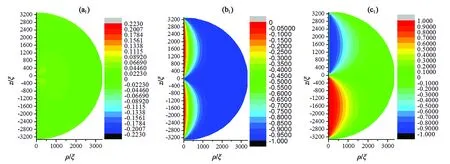

4.3 電場效應

5 結 論

