結合分數階微分及Retinex的NSCT自適應低照度圖像增強

林劍萍，廖一鵬

(1. 陽光學院 人工智能學院，福建 福州 350015;2. 福州大學 物理與信息工程學院, 福建 福州 350108)

1 引 言

低照度圖像對比度較低，細節丟失嚴重，不利于人眼觀察和計算機視覺算法的使用。因此，有效的圖像增強算法對后續圖像分析和圖像理解非常重要。

圖像增強的主流算法包括：直方圖均衡化、Retinex、分數階微分、模糊集理論及多尺度變換等[1-2]。直方圖均衡化的增強算法，整體對比度有明顯提高，但會出現過增強、微弱信息被丟失的情況[3-5]。萬智萍[6]等提出的結合人眼視覺特性與直方圖均衡化的增強算法，改善了圖像的整體視覺效果，但不可避免地出現微弱信息丟失、放大噪聲以及局部信息被弱化等情況。Land[7]等人提出的 Retinex 理論被廣泛用于圖像增強，其中最經典的是單尺度 Retinex(Single scale Retinex，SSR)[8]與多尺度 Retinex(Multi-scale Retinex，MSR)[9]算法，它們均以高斯濾波器作為低通濾波器， 雖然算法簡單，但增強后的圖像光暈現象嚴重，且算法是基于時域的增強方法，處理低照度圖像時會出現細節丟失、邊緣模糊等現象。Elad[10]等提出基于雙邊濾波(bilateral filter)的 Retinex 算法, Wang[11]等提出基于引導濾波(guided filter)[12]的 Retinex 算法， 張詩[13]等提出的基于Retinex的引導濾波變分框架低照度圖像增強算法， 盡管這些濾波器具有一定的保邊平滑能力, 但在維持保邊能力的同時難以做到對圖像充分平滑, 使得照度圖像估計仍然存在偏差。云海姣[14]等人提出了結合直方圖均衡和模糊集理論的紅外圖像增強，克服了過增強和局部信息被弱化等問題，但是在計算能力、去模糊化等方面的效果仍有待加強。國外學者提出多尺度理論后，基于變換域如Wavelet 變換、Contourlet 變換及非下采樣 Contourlet 變換的增強算法大批涌現。在國內，朱國慶[15]等人提出一種基于人類視覺系統的亮度掩蔽和對比度掩蔽特性的NSCT 域紅外圖像增強算法, 該算法能夠有效地對圖像局部和整體進行增強, 同時能夠避免產生過增強現象,但圖像紋理細節還不夠豐富。陳慶利[16]等人提出的基于分數階微分的增強算法，能使紋理細節信息豐富，但整體動態范圍呈現壓縮趨勢，不便于人眼觀察。朱丹丹[17]等人提出了Contourlet變換和遺傳算法相結合的瀝青紅外圖像增強方法，能有效地抑制噪聲,提高清晰度，但會出現“混疊”現象。曹美[18]等人提出的基于非下采樣 Contourlet 變換的增強算法，并結合直方圖均衡化，能有效提高圖像的整體效果，同時能抑制噪聲的放大，但對局部的增強不太理想；Cao[19]等人提出了基于NSCT和分數微分的深度圖像增強與檢測方法，該方法能有效地增強圖像的深度和檢測噪聲，但在處理復雜物體和室外光線情況時仍然是一個挑戰。

針對上述算法的不足，本文結合NSCT變換和改進的Retinex、分數階微分，對低照度圖像進行多尺度增強處理。首先將圖像NSCT多尺度分解，獲得低頻子帶圖像和高頻子帶系數，結合改進的Retinex算法對低頻分量進行增強，提高圖像輪廓的清晰度，擴展其灰度級的動態范圍；然后將高頻經Bayes閾值隔離噪聲后利用自適應分數階微分進行增強，提升圖像的邊緣和紋理細節；最后對處理后的圖像進行NSCT重構，獲取增強后的低照度圖像。將本文算法與其他增強算法進行主觀與客觀的對比和分析，本文算法克服了上述算法存在的光暈現象、模糊現象、細節丟失和“混疊”等現象，改善了圖像整體的視覺效果。

2 NSCT域低照度圖像增強

2.1 低照度圖像NSCT分解

Contourlet 變換能較為理想地描述或表征光滑曲線的邊緣，但不可避免地產生頻譜混疊失真現象。NSCT變換主要是通過一種迭代方式獲得多分辨率、高冗余度、多方向及各向異性的表示方法[20]。在分解和重構過程中，都沒有涉及到下采樣，使其擁有平移不變性。NSCT變換的結構與Contourlet變換類似，如圖1所示。

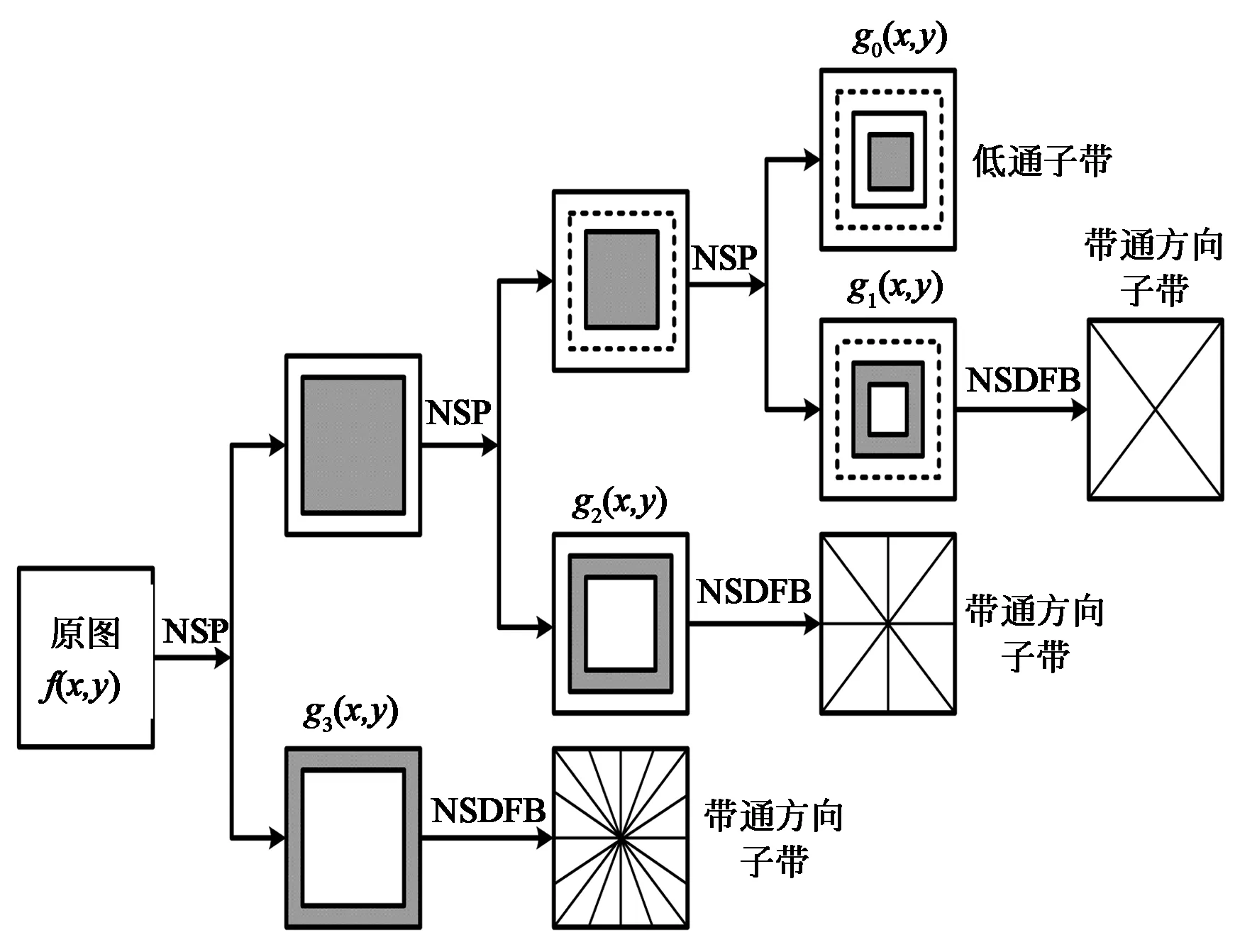
圖1 NSCT變換三級分解結構圖Fig.1 Three-level decomposition structure of NSCT transform

NSCT變換根據獨特濾波構造實現多尺度分解，首先由NSP對輸入圖像進行塔形分解，得到低頻子帶和多個帶通子帶，然后采用非下采樣方向濾波器組(NSDFB)對各個帶通子帶進行多方向分解，得到多個不同方向的高頻子帶圖像，最后得到一個低頻近似圖像和多個不同尺度方向的高頻子帶圖像，而且這些圖像的分辨率都和原始圖像相同。

2.2 低頻子帶改進雙邊濾波Retinex增強

一般情況，待處理圖像經過 NSCT 變換分解得到的低頻分量集中反映的是大量的基本信息，也就是其輪廓，一般不含有噪聲。因此，對低通子帶系數處理的關鍵是要擴展其灰度級的動態范圍。相比于傳統的線性、非線性算法只能增強圖像的某一特征，Retinex 算法可以在顏色恒常、對比增強、動態范圍壓縮等方面達到平衡，增強效果尤為顯著[21]，故本文采用 Retinex 算法并加以改進。

Retinex 模型對理想圖像的定義，可以表述為：

f(x,y)=r(x,y)×i(x,y)，

(1)

式中：f(x,y)為理想圖像；i(x,y)為照度圖像，其根據場景的不同照明程度而變化；r(x,y)為反射圖像，其與場景本身的自然屬性相關，通常體現的是場景的細節特征，與照度分量沒有絲毫的相關性。

Retinex圖像增強的目的就是從待處理圖像f中估計出照度圖像i，同時去除照度分量信息i，從而分解出反射圖像r，消除或降低光照不均的影響，以改善圖像的視覺效果。一般做法是：將圖像轉至對數域，從而將乘積關系轉換為和的關系，如式(2)所示；然后歸一化去除圖像照度分量；將去除了照度分量的圖像求指數，反變換到實數域后輸出。

lg[f(x,y)]=lg[r(x,y)×i(x,y)]=
lg[r(x,y)]+lg[i(x,y)]，

(2)

算法流程如圖2所示。

圖2 Retinex算法流程圖Fig.2 Algorithm flow char of Retinex

一般的Retinex算法在對光照圖像估計時，都會假設初始光照圖像是緩慢變化的，即光照圖像是平滑的，但實際情況并非如此，在亮度相差很大的區域邊緣處，圖像的光照變化是不平滑的，在這種情況下，Retinex算法在此區域會出現 “光暈”現象。

本文對Retinex算法進行改進，具體如下：

借助非線性的雙邊濾波函數估計其照度分量。通過空間鄰域濾波器和值域濾波器進行光照強度的改變，雙邊濾波算法定義為：

(3)

歸一化函數表述為：

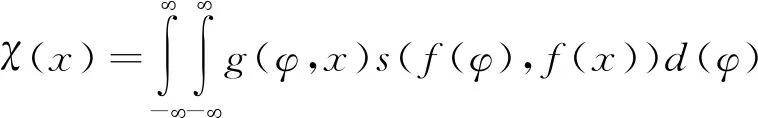
(4)

式中：f(x)表示原始圖像在點x處的灰度值，h(x)表示輸出圖像在點x處的灰度值，g(φ,x)表示臨近點φ與中心點x之間的距離相似程度，s(f(φ),f(x))表示臨近點φ與中心點x之間的灰度相似程度。雙邊濾波的距離相似度和灰度相似度都取參數為歐氏距離的高斯核，具體如下：

(5)

式中，d(φ,x)=‖φ-x‖表示φ與x兩點之間的歐式距離。

(6)

式中，δ(φ,f)=‖φ-f‖表示φ與f2個灰度值之差。

照度分量表示圖像的動態范圍，需對其進行校正。Gamma校正(冪律變換)是一種重要的非線性變換，是對輸入圖像灰度值進行指數變換，可以提高圖像的動態范圍，主要運用在圖像增強，目標檢測及圖像分析等領域。本文采用Gamma校正函數校正照度分量。表示如下：

(7)

式中：γavg′為校正后的照度分量，γ1、γ2分別為兩濾波器的照度，Kavg為自變量Kavg1、Kavg2由人為進行設定。

反射分量中也存在許多重要特征信息，適當的校正可以豐富其層次性，本文利用影響因子對其進行校正，校正公式表述為：

?′=α×?，

(8)

式中：α為影響因子，即增強的倍數，?為反射分量。

改進Retinex算法的實現如圖3所示。先將圖像轉至對數域，借助非線性的雙邊濾波函數進行照度估計，然后利用Gamma校正函數，對輸入圖像的照度分量灰度值進行指數變換，完成照度校正；將去除了照度分量的圖像求指數，反變換到實數域，利用影響因子校正其反射分量；最后將校正過的照度分量和反射分量相乘后輸出。該算法增強了圖像的整體輪廓，擴展其灰度級的動態范圍，克服了光暈和模糊現象。

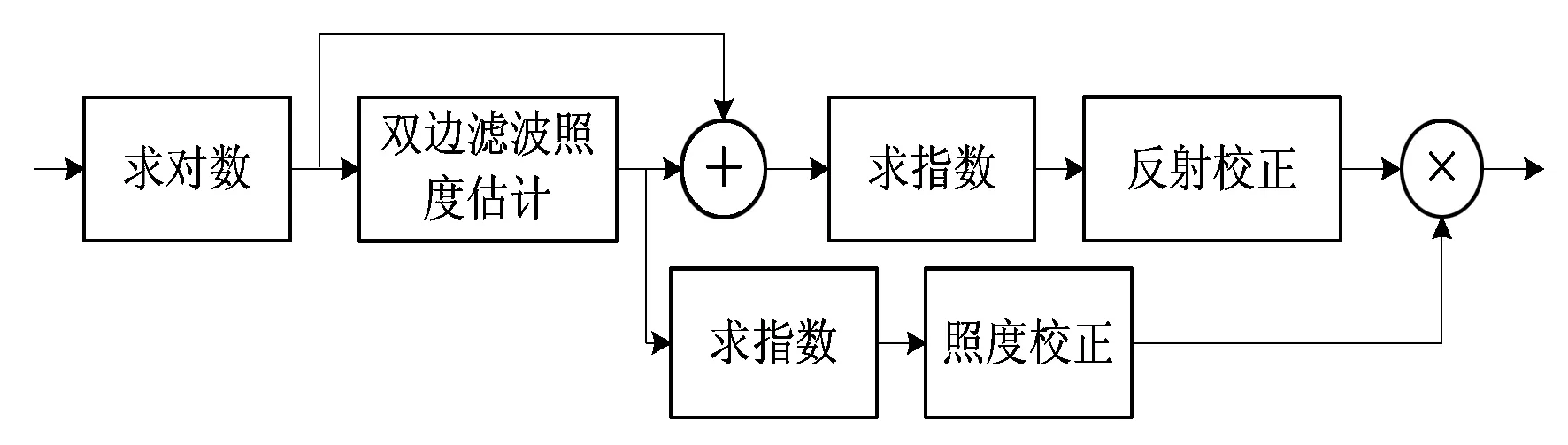
圖3 改進Retinex算法的實現Fig.3 Implementation of improved Retinex

2.3 高頻子帶的自適應分數階微分增強

經過NSCT變換分解得到的高頻方向子帶系數往往包括大部分的邊緣信息、紋理細節及幾乎全部的噪聲。一般情況下，復雜紋理和細節及弱邊緣特征信息出現在子帶絕對值較大的系數間，故需要將其進行保留或增強處理，而噪聲存在于高頻子帶中絕對值較小的系數中，會影響圖像整體效果，需加以抑制。為了達到更為理想的增強效果，將分解得到的高頻子帶系數進行Bayes Shrink閾值處理，不同尺度、不同方向上小于閾值的系數將其置0，對大于閾值的系數進行保留，并對保留后的系數利用改進分數階微分算法做進一步的增強處理。

2.3.1 Bayes Shrink閾值去噪

由Bayes Shrink閾值函數T構造得：

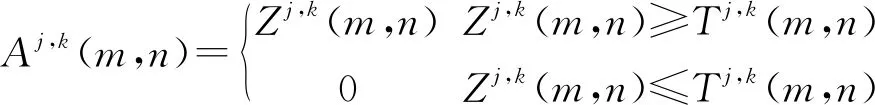
(9)

式中：Zj,k(m,n)為第j尺度、第k方向的NSCT系數，Tj,k(m,n)為局部閾值，其計算公式如式(10)所示：

(10)

式中：σj,k為噪聲的標準差，σz(m,n)為信號的局部標準差，其計算公式如式(11)和式(12)所示：

(11)

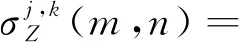
(12)

2.3.2 改進分數階微分算法

目前Riemann-Liouville(R-L)定義、Grumwald-Letnikov(G-L) 定義、Caputo定義是比較經典的分數階微分定義。在數字圖像處理中， G-L 定義得到廣泛的應用，其數學表達式為：

(13)

其中：D表示此式為分數階微積分，GL表示該分數階微分采用Grumwald-Letnikov(G-L)定義，h表示積分時間步長。

若f(t)的持續期t∈[a,b]，將函數持續期間[a,b]按單位間隔h=1進行等分，得到：

(14)

則一元函數f(t)的v階分數階微分差分表達式為：

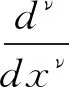
(15)

求取5×5八方向的分數階微分掩膜算子，并疊加得到圖4所示的掩膜。

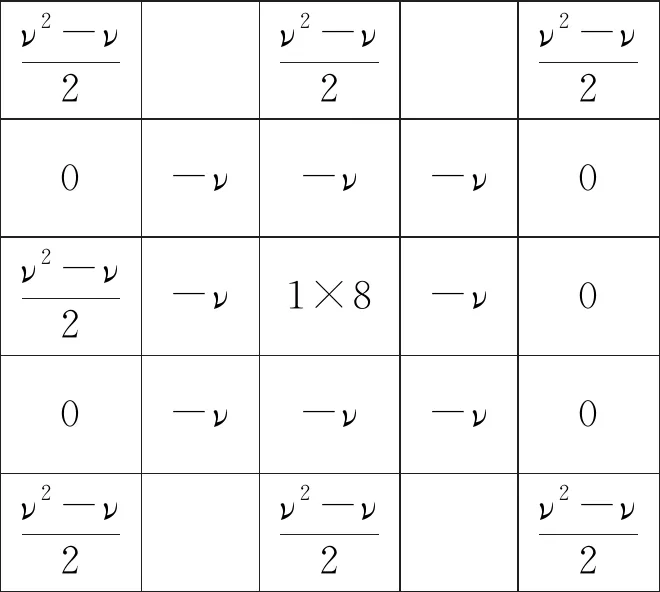
ν2-ν2ν2-ν2ν2-ν20-ν-ν-ν0ν2-ν2-ν1×8-ν00-ν-ν-ν0ν2-ν2ν2-ν2ν2-ν2

圖4 8個方向偏微分疊加后的掩膜

Fig.4 Mask superposed by partial integrals of 8 directions

文獻[22]、[23]證明，相較于整數階微分，分數階微分進行邊緣檢測時，不僅能夠很好提取圖像邊緣信息，而且還能夠對平滑區域的弱邊緣信息有很好的保留。

(1)Otsu算法選取最佳閾值

閾值的選取尤為關鍵，閾值的好壞直接決定了圖像的增強效果。Otsu算法即最大類間方差法，其魯棒性強、實時性和精準性高[24]。但傳統的二維Otsu算法難以精準識別圖像的邊緣和紋理信息。李博[25]等對傳統的二維Otsu算法進行改進，以所選圖像的梯度為對象，關聯像素點與鄰域像素點的信息，同時構建二維直方圖，并借助整體輪廓與邊緣細節的類間方差的極大值獲得最優閾值。

對于待處理圖像f(i,j),L為灰度級數，M(i,j)為像素點(i,j)各方向上梯度平均值的集合統稱，N(i,j)為像素點(i,j)各鄰域梯度的平均值。

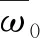
(16)

(17)

上面兩式所對應的均值μ0與μ1分別表述為：

(18)

(19)

由μ0與μ1兩向量構成的二維直方圖的均值μT可表述為：

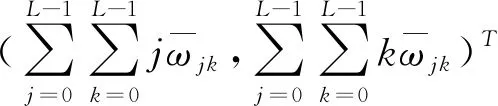
(20)

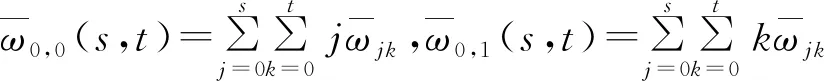
由于分布在對角線位置的數值較小且對最終的結果影響不大，故可忽略不計。因此，類間的散度矩陣SB即最佳閾值，可表述為：

(21)

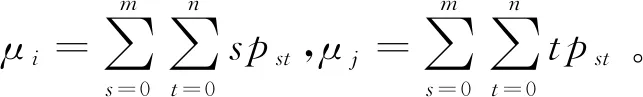
(2)確定最優階數v進行自適應增強

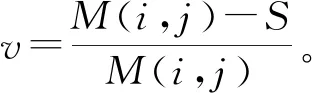
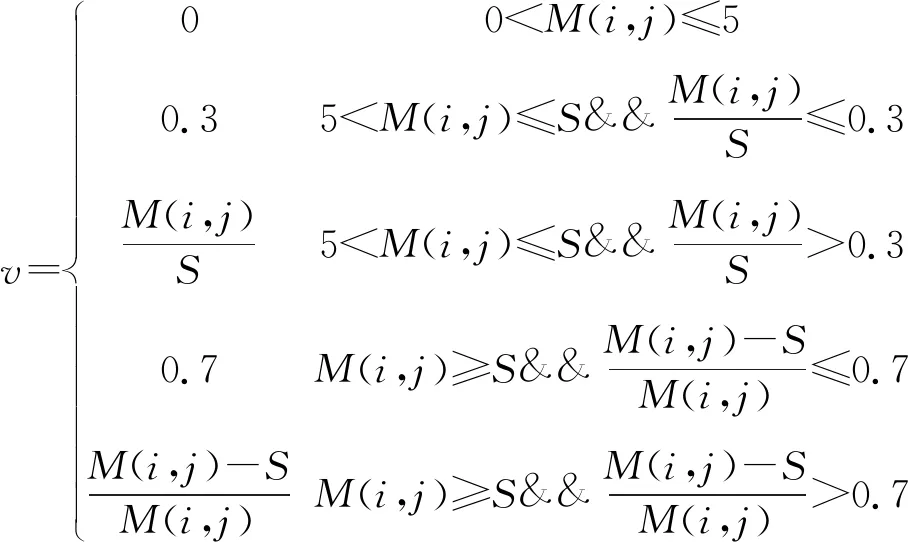
(22)

圖5 自適應分數階微分算法的實現Fig.5 Implementation of adaptive fractional differential algorithms

自適應分數階微分算法的實現如圖5所示。求待處理圖像f(i,j)像素點(i,j)各方向上梯度平均值的集合M(i,j)，像素點(i,j)各鄰域梯度的平均值N(i,j)。利用Otsu算法選取最佳閾值S，再用構造的分數階微分的分段函數優化分數階微分的階數v，再把v代入掩膜算子，從而實現對分解獲得的高頻方向子帶系數進行自適應分數階微分增強。

3 本文算法流程與步驟

綜上分析，文中低照度圖像多尺度增強算法流程如圖6所示，具體實現步驟如下：

Step 1：經配準、校正等預處理后，采用NSCT變換對原始圖像進行多尺度多方向的分解；

Step 2：經NSCT多尺度變換分解后，得到低頻子帶近似分量，并根據雙邊濾波器的特性來估計照度分量，同時反射分量與照度分量借助影響因子α、Kavg來分別進行校正，從而對低頻子帶系數實現改進Retinex算法的增強；

Step 3：求取像素梯度均值M和鄰域梯度均值N，根據二維Otsu算法選取最佳閾值S，并通過式(18)設定的分段函數來優化分數階微分的階數v，從而對分解獲得的高頻方向子帶系數進行自適應分數階微分增強；

Step 4：對處理后的低頻子帶系數和高頻方向子帶系數進行NSCT反變換，從而獲得增強后的圖像。

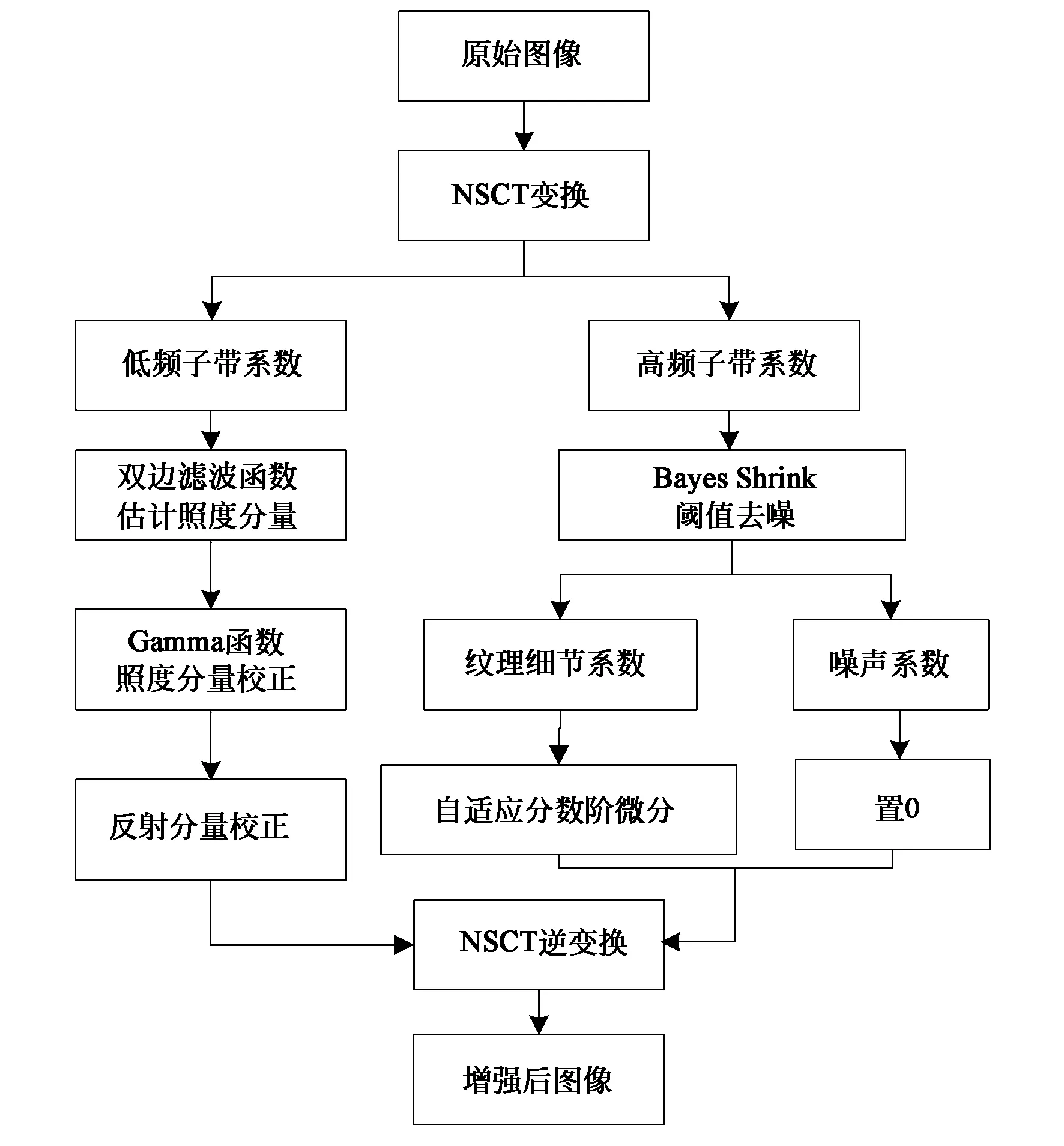
圖6 本文增強算法流程圖Fig.6 Flowchart of strengthened algorithm in this paper

4 實驗仿真結果與分析

本文從Athena攝像機系統注冊的數據庫圖像中，選取不同場景的2幅紅外夜視圖像和2幅低亮度可見光圖像分別進行仿真實驗，如圖7和圖10所示。實驗在臺式機(Windows 10操作系統，CPU：Pentium，RAM：4 GB)上采用Matlab R2016a軟件進行仿真。其中，小波變換采用“db4”小波包進行4層分解，而Contourlet變換以及NSCT變換均采用金字塔濾波器為“9-7”濾波器，方向濾波器組采用“dmaxflat”濾波器，分解的尺度均設定為3級，且每一級分解后所對應的子帶方向數分別為2，4，8。實驗過程中，為了更好地評判所提算法是否具有優越性，本文將此算法與CLAHE(Contrast Limited Adaptive Histogram Equalization)算法、FD(fractional differential，v=0.6)算法、MSR(Multi-Scale Retinex)算法、基于Wavelet變換算法、基于Contourlet變換算法、基于NSCT變換算法、文獻[14]算法以及文獻[15]算法進行對比實驗，首先從人眼視覺感知的主觀角度進行效果描述，再借助對比度(CR)、清晰度(AG)以及信息熵(IE)進行客觀分析。對比度大的圖像通常層次感強，清晰度高，其計算公式為：

(a) 實驗圖像1(a)Experimental image 1

(b) 實驗圖像2(b) Experimental image 2

(23)

其中：δ(i,j)=|i-j|，即相鄰像素間的灰度差，pδ(i,j)即相鄰像素間的灰度差為δ的像素分布概率。清晰度是圖像的平均梯度，可以敏感地反映圖像對細小反差表達的能力，可用來評價圖像的清晰程度，同時反映出圖像中微小細節反差和紋理變換特征。其公式為：

(24)

其中:F為目標圖像，M、N分別為圖像F的行數與列數。

信息熵的定義為：

(25)

對于一幅單獨的圖像，可以認為其各像素的灰度值是相互獨立的樣本，則這幅圖像的灰度分布為p={p0,p1,…，pi…，pL-1},pi為灰度值等于i的像素與圖像總像素之比，L為圖像總像素的灰度級。

4.1 紅外夜視圖像增強效果分析

通過圖8可以發現，圖8(a)相比于原始圖像，好像去了層“霧”，目標行人也較為清晰，但筑臺周邊的沙堆紋理等細節不易識別；圖8(b)中的目標行人還算清晰，筑臺的黑色紋理容易識別出來，但整體對比度偏暗；圖8(c)中的目標行人清晰可見，沙堆紋理也有一定凸顯，但引入了部分噪聲造成沙堆模糊化；圖8(d) ～(f)是基于多尺度幾何變換實現的，取得了一定的效果，紋路也更為細膩，但增強效果還有待進一步提高；圖8(g)和圖8(h)相比于前面幾幅圖，效果更為顯著，其在增強對比度的同時能保留較多的紋路信息。但本文算法(圖8(i))能更有效地改善圖像的動態范圍，灰度色彩更為飽滿，如行人及筑臺黑色條紋清晰可見，彌補了類似過增強、細節丟失、局部信息被弱化及模糊化等不足，更具有豐富的邊緣、細節等特征信息，如筑臺兩側的石頭能清楚地辨識。

圖8 紅外圖像1用不同增強算法的效果對比圖Fig.8 Comparison map of infrared image 1 processed with different enhancement algorithms

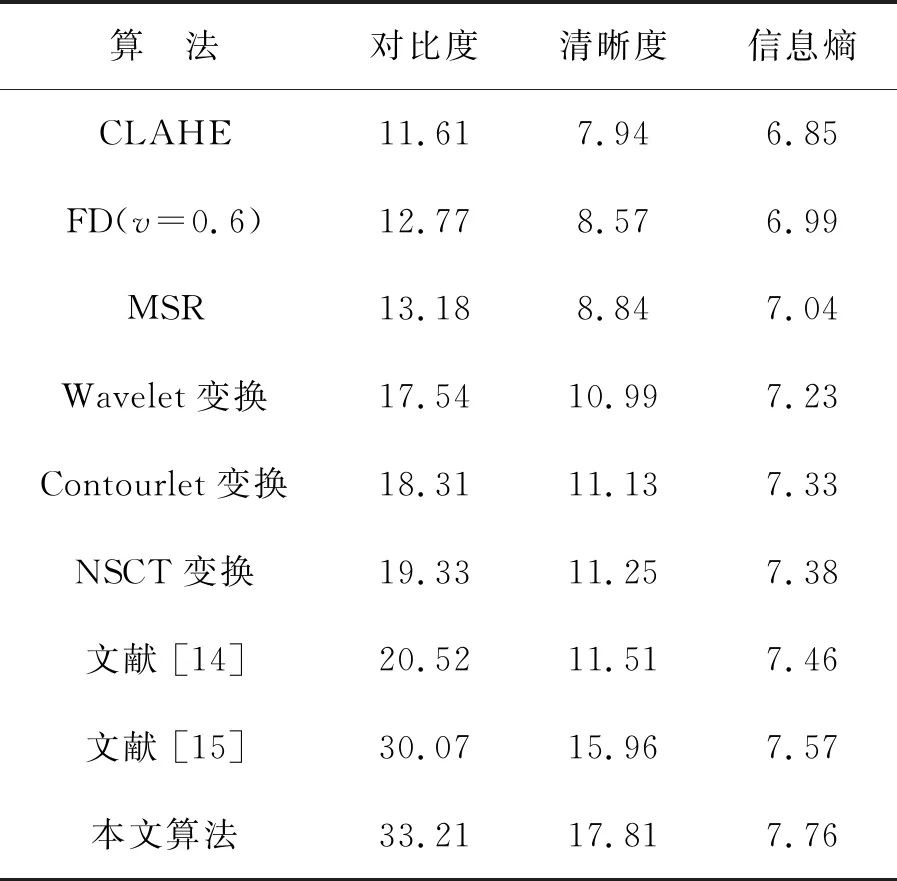
從表1中的數據也可以發現，各種算法的對比度、清晰度及信息熵呈現逐漸提高的態勢，且本文算法的3個評價參數的數值均要高于其他幾種增強算法，相比于增強效果較為顯著的文獻[15]，對比度、清晰度及信息熵分別提高了10.4%，11.6%，2.5%。正好印證了主觀上的效果評價，可以讓圖像看起來更自然，更符合人眼視覺的直觀感受。

表1 各種算法處理實驗圖像1后的客觀數據

Tab.1 Objective data of experimental image 1 processed with various algorithms

算 法對比度清晰度信息熵CLAHE11.617.946.85FD(v=0.6)12.778.576.99MSR13.188.847.04Wavelet變換17.5410.997.23Contourlet變換18.3111.137.33NSCT變換19.3311.257.38文獻 [14]20.5211.517.46文獻 [15]30.0715.967.57本文算法33.2117.817.76

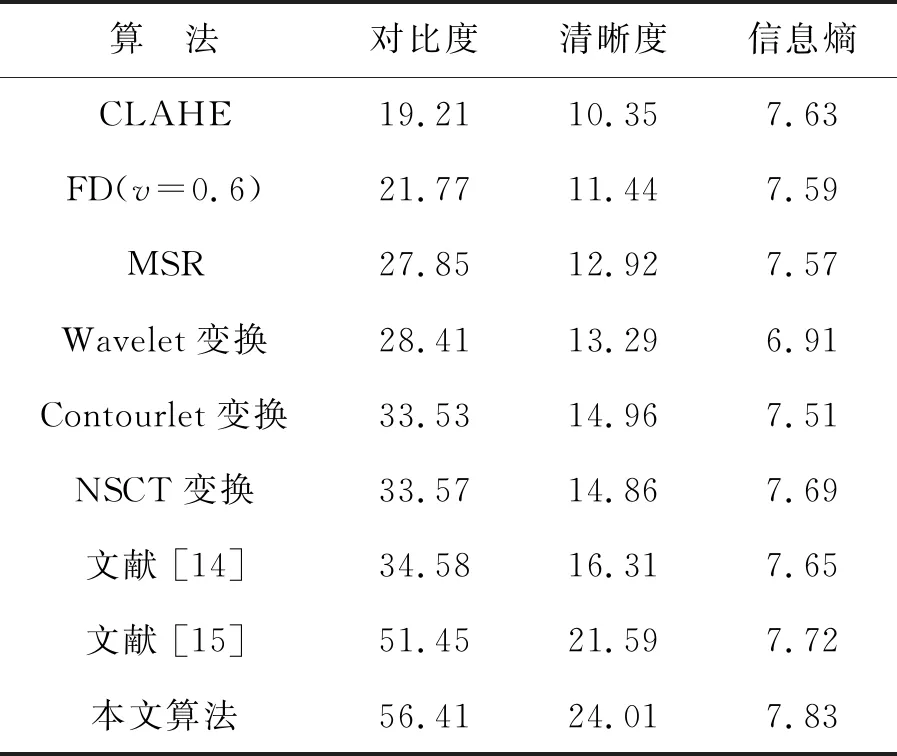
通過圖9可以發現，相比于原始圖像，圖9(a)能較好地去除“白霧”，有一定的增強效果，房屋、樹木及柵欄較清晰，但路面的紋路丟失嚴重；圖9(b)的視覺效果還可以，且比圖9(a)具有更為豐富的路面紋理特征，但整體視覺效果有待改善；圖9(c)中的云層、房屋、樹木以及柵欄清晰可見，路面紋理也有一定的凸顯，但頂部背景信息偏暗；圖9(d)～(f)均取得了一定的效果，紋路也較為細膩，但動態壓縮范圍有待提高；圖9(g)和圖9(h)的路面紋理脈絡較細致，能給人直觀的畫面感。但本文算法(圖9(i))整體效果更為清晰可見，且道路紋理、道路中的白帶及屋頂的烏云邊緣等紋理均能很好地展現給觀察者。從客觀角度出發，表2中的數據可以發現，本文算法的對比度、清晰度及信息熵也均高于其他幾種增強算法，相比于文獻[15]，對比度、清晰度及信息熵分別提高了9.6%，11.2%，1.4%，這對后續的識別、跟蹤及特征提取極為有利。

圖9 紅外圖像2用不同增強算法的效果對比圖Fig.9 Comparison map of infrared image 1 processed with different enhancement algorithms

4.2 低亮度可見光圖像增強效果分析

與紅外圖像增強效果類似，圖10(a)中的原始圖像好像被蒙上了一層紗，草叢中的細節信息也被“白霧”化。處理后，通過圖11可以發現，圖11(a)中的樹叢更為明朗，且飛機也更容易觀察到，與此同時，草叢的弱紋理細節呈現“白霧”化，細節丟失嚴重；圖11(b)能在去“霧”的同時，保留了草叢中的部分細節信息，但飛機、樹叢等特征的亮度偏暗，讓整體圖像看起來不明朗；圖11(c)與圖11(b)相比，有相似的對比度，且紋理特征信息有所體現，但丟失了大部分的微弱信息；圖11(d) ～(f)均取得了一定的效果，草叢紋路也較為細膩，但動態壓縮范圍有待提高；圖11(g)和圖11(h)中的草叢紋理部分脈絡較細致，有一定的“還原”作用，能給人直觀的畫面感，但圖11(g)的樹木看起來不那么真實，會出現“閃爍”的白點，圖11(h)中最右邊的那棵樹偏暗，與實際場景不匹配；本文算法避免了局部信息被弱化和細節不完整，圖11(i)中的草叢更為飽滿，飛機、草叢及樹叢分布看起來更加自然。從表3中數據同樣可以看出，3種參數呈現逐漸遞增的趨勢，且相比于文獻[15]分別提高了13.4%，10.1%，1.5%，這與主觀人眼察覺效果相匹配，進一步印證了本文算法的優秀特性。

表2 各種算法處理紅外圖像2后的客觀數據

Tab.2 Objective data of infrared image 2 processed with various algorithms

算 法對比度清晰度信息熵CLAHE19.2110.357.63FD(v=0.6)21.7711.447.59MSR27.8512.927.57Wavelet變換28.4113.296.91Contourlet變換33.5314.967.51NSCT變換33.5714.867.69文獻 [14]34.5816.317.65文獻 [15]51.4521.597.72本文算法56.4124.017.83

(a) 實驗圖像1(a)Experimental image 1

(b) 實驗圖像2(b) Experimental image 2

圖11 可見光圖像1用不同增強算法的效果對比圖Fig.11 Comparison map of visible image 1 processed with different enhancement algorithms

表3 各種算法處理可見光圖像1后的客觀數據

Tab.3 Objective data of visible image 1 processed with various algorithms

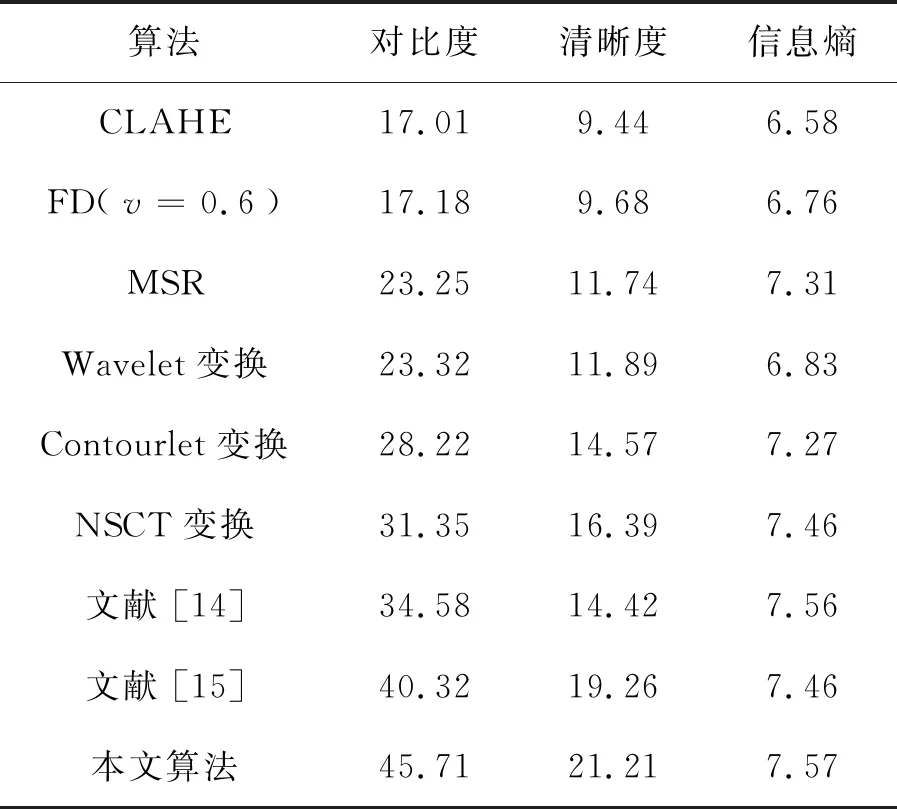
算法對比度清晰度信息熵CLAHE17.019.446.58FD(v=0.6)17.189.686.76MSR23.2511.747.31Wavelet變換23.3211.896.83Contourlet變換28.2214.577.27NSCT變換31.3516.397.46文獻 [14]34.5814.427.56文獻 [15]40.3219.267.46本文算法45.7121.217.57

圖12 可見光圖像2用不同增強算法的效果對比圖Fig.12 Comparison map of visible image 2 processed with different enhancement algorithms

與圖10(a)不同的是，圖10(b)中原始圖像的細節信息較不明顯，如飛機的螺旋槳，由于飛行高度非常高，導致背景區域信息不易識別，如相間的山谷與山峰。通過圖12中不同算法的實驗仿真得知，圖12(a)～(e)對背景信息有一定的增強效果，類似“網狀”條紋能比較清楚地識別出，但機身、螺旋槳等目標信息看起來偏暗，導致整體視覺效果偏差；圖12(f) ～12(h)相比于前面幾種算法，它們均能近似還原飛機的原始模樣，螺旋槳等細節信息也能很好地體現出來。因此，從主觀上看不出本文算法的優勢。通過表4中3個參數的數據得知，本文算法的數據最優，且相比于文獻[15]分別提高了9.5%，6.4%，3.7%，能很好地說明本文算法優于其他算法。

表4 各種算法處理可見光圖像2后的客觀數據

Tab.4 Objective data of visible image 2 processed with various algorithms

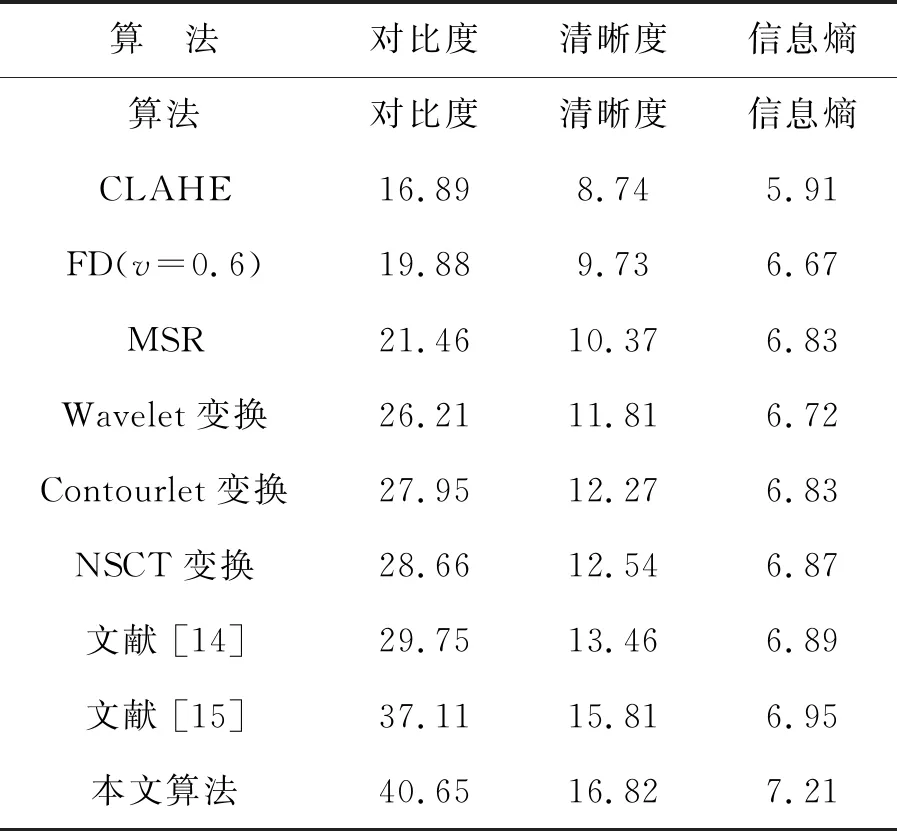
算 法對比度清晰度信息熵算法對比度清晰度信息熵CLAHE16.898.745.91FD(v=0.6)19.889.736.67MSR21.4610.376.83Wavelet變換26.2111.816.72Contourlet變換27.9512.276.83NSCT變換28.6612.546.87文獻 [14]29.7513.466.89文獻 [15]37.1115.816.95本文算法40.6516.827.21

5 結 論

針對Retinex算法處理低照度圖像時會出現細節丟失、邊緣模糊等現象，文中提出了一種基于非下采樣Contourlet變換、結合改進Retinex及分數階微分的圖像增強算法。采用改進的Retinex對低頻子帶圖像進行增強處理，主要做法是引入非線性的雙邊濾波函數估計待處理圖像的照度分量，并對處理后的照度分量及反射分量進行校正操作，消除了“光暈”現象的同時改善了圖像視覺效果。針對傳統固定階次的分數階微分算法存在的諸多缺陷，根據圖像鄰域分布特征，求取像素梯度均值及鄰域梯度均值，通過二維Otsu算法獲得最佳閾值，并通過預設定的分段函數確定最優階數，自適應進行增強處理，使圖像的邊緣、紋理等細節更加清晰。實驗結果表明，本文算法的對比度、清晰度及信息熵均高于其他幾種增強算法，相比于文獻[15]分別提高了10.7%，9.8%，2.3%。本文算法處理后的圖像在細節、邊緣保持等方面都優于其他算法，改善了圖像視覺效果。