積累基本活動經驗 落實數學核心素養

于濤

[摘要]文章以“兩角差的余弦公式”教學設計為例，創新教學活動，從幾何直觀到代數推理，引導學生經歷數學實踐活動和思維活動，積累基本活動經驗，培養數學核心素養，

[關鍵詞]基本活動經驗;核心素養;兩角差的余弦公式

《普通高中數學課程標準（2017年版）》指出：通過高中數學課程的學習，學生能獲得進一步學習以及未來發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗（簡稱“四基”），《課標（2017年版）》將“雙基”提升為“四基”，首次提出基本活動經驗是數學學習的基礎，史寧中教授認為，數學活動既應包含具體身體行動的活動，也應包括數學思維活動，這樣基本活動經驗主要就是兩個經驗：一個是學生的實踐經驗，培養學生的數學直觀：另一個是學生的思維經驗，培養學生會思考問題，因此，數學基本活動經驗滲透在整個數學教學中，成為落實數學核心素養的有效途徑，下面以“兩角差的余弦公式”為例，談談通過恰當創設教學活動，引導學生積累基本活動經驗，培養數學核心素養。

1基本情況

1.1教材內容分析

兩角差的余弦公式是在學習三角函數、向量等知識后，研究的第一個兩個角的三角計算公式，它是研究其它兩角和差公式、倍角公式的基礎，具有承上啟下的作用，從知識生成的過程看，本節課的知識源白天文學的測量問題，涉及幾何圖形的長度、面積、角度等度量問題，從推導公式的過程看，需要應用單位圓等數學模型，聯系三角函數、向量等知識。

1.2學生學情分析

學生在初中學習了用直角三角形定義銳角三角函數，在高中學習了用單位圓定義任意角三角函數，從靜態的銳角到動態的任意角，學生先后學習了兩個重要數學模型：直角三角形和單位圓，但還不能將解決角的問題與應用數學模型相結合，另外，學生在初中學習勾股定理及其證明時，初步體會了將幾何圖形的相互關系（面積關系）轉化為代數表示（勾股定理），具備了一定的直觀想象意識。

1.3教學目標設置

（1）借助勾股定理的證明方法，回顧用幾何圖形的相互關系研究代數關系的基本思路，發展學生提出問題的能力：

（2）結合活動探究，經歷從幾何直觀到代數表示，初步得到兩角（銳角）差的余弦公式，培養幾何直觀素養：

（3）會用任意角的單位圓模型證明兩角差的余弦公式，感悟從具體到抽象、特殊到一般、數形結合等基本思想，培養邏輯推理素養：

（4）通過例題及變式的教學，掌握兩角差的余弦公式，培養數學運算素養：

（5）借助探究性作業，深化基本活動經驗，發展學生的創新意識，

重點：兩角差的余弦公式，

難點：兩角差的余弦公式的生成與推廣過程，

2教學過程

2.1復習回顧，創設情境

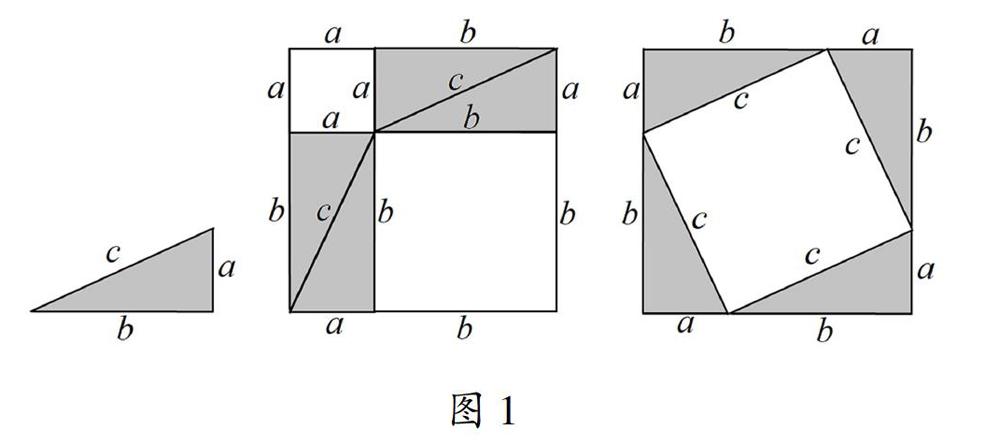
問題1如圖1.說說初中課本勾股定理證明方法的思路和基本思想？

學生：用四個全等Rt△構造出兩個全等正方形，根據兩個圖形中陰影部分和空白部分的面積分別相等，得到a²+b²=c²體現了數形結合的基本思想。

教師：這個方法體現了形數統一，既嚴密又直觀，

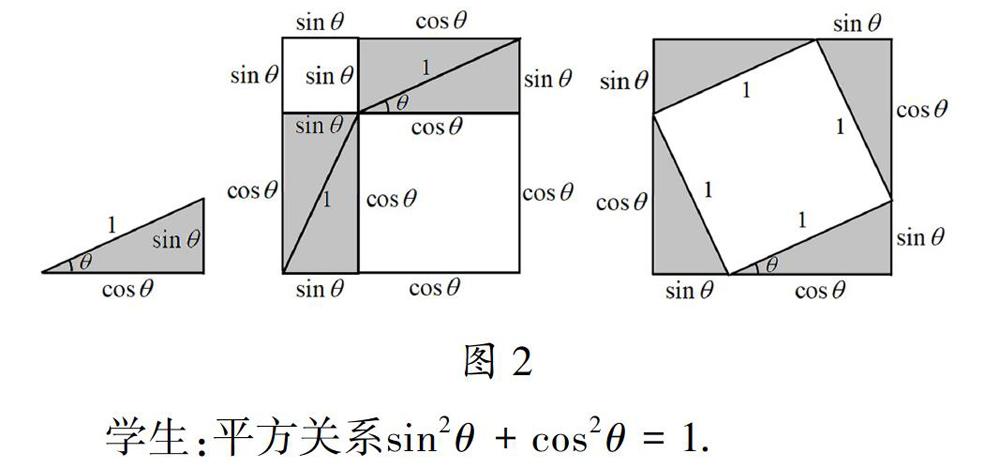
問題2幾何圖形的度量和計算除了長度、面積，還有角度，如圖2.若直角三角形斜邊長為1.其中一個銳角為θ，請仿照勾股定理的證明思路，說出有關θ的等式。

學生：平方關系sin²θ+cos²θ=1

教師：不過這個幾何圖形（圖2）只能證明銳角平方關系，要證明任意角平方關系需要用單位圓模型。

設計意圖

勾股定理的證明是通過對幾何圖形的拼接、割補來證明代數關系的，證明過程重在通過對幾何圖形的度量和計算，將幾何關系轉化為代數表示，是以形證數的典范，以此喚醒學生直觀想象的意識，鑒于幾何度量不僅包含長度、面積，還包含角度，通過相同圖形，不同代數觀測，得到不同的代數表示，培養學生學會用數學的眼光觀察幾何圖形，發展學生提出問題的能力，從長度到角度，用圖1、圖2分別證明勾股定理和平方關系（銳角）的思維過程是類似的，是探究發現兩角（銳角）差的余弦公式的重要活動經驗。

2.2合作交流，探究發現

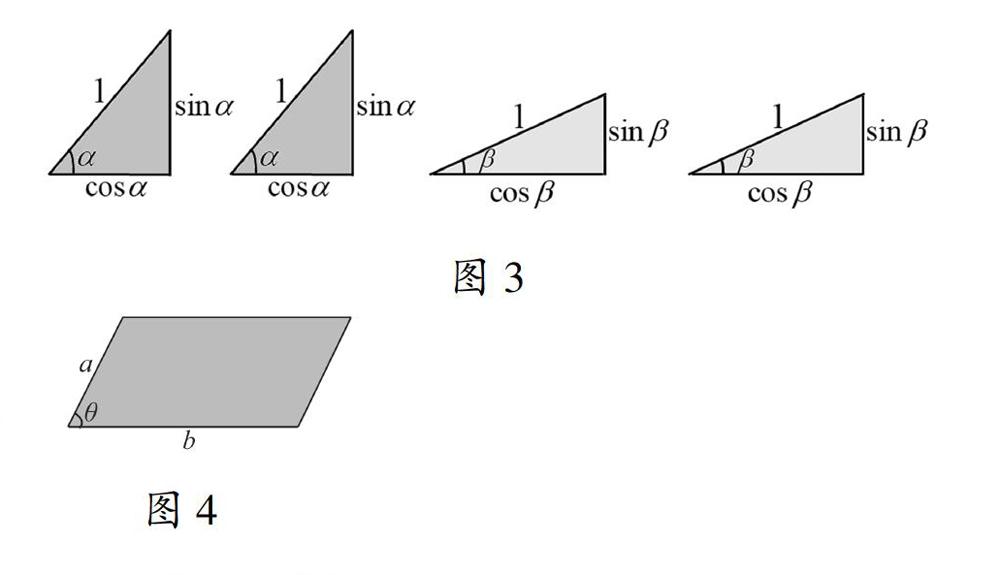
活動：請用兩對斜邊長為1的直角三角形（如圖3），其中一對含銳角α，另一對含銳角β，仿照勾股定理的證明思路，探究有關α與β的等式，（注：學生每人兩對直角三角形，同桌為一組）

公式：平行四邊形面積公式（如圖4）：S□=absinθ

探究結果展示：（請一個小組分享，簡述證明思路）

教師：這個公式就是兩角差的余弦公式，但是只證明了α和β是銳角的情形。

設計意圖

活動的創設是問題2的變式，從四個全等直角三角形的一個銳角的等量關系的發現，到兩組全等直角三角形的兩個銳角的等量關系的探究，讓學生經歷證明勾股定理的思維過程，積累通過幾何圖形發現數學結論的活動經驗，培養學生幾何直觀素養，從一個角到兩個角，讓學生感悟數學問題產生、發展的方法，發展學生發現、提出問題的能力，

2.3推導證明，公式推廣

問題3如何證明對任意角α，β∈R，cos（α-β）=cosαcosβ+sinαsinβ？

教師：我們用直角三角形的三邊關系定義了銳角三角形函數，探究活動用直角三角形拼接幾何圖形證明了兩角（銳角）差的余弦公式，要將其推廣至任意角，說說你的想法？

學生：可以考慮用單位圓模型來證明，

教師：如圖6.分別畫出角α，β的終邊，寫出終邊與單位圓交點A，B的坐標，那么，角α-β如何在圖中表示？（根據學生的回答，出現了兩種思路）

設計意圖按照初、高中學習三角函數定義的順序，先用直角三角形拼接幾何圖形進行公式的探究與發現，再用單位圓模型進行公式的推廣與證明，從具體到抽象、特殊到一般，符合學生的認知規律，對于兩種證明方法，思路一代數多于幾何，緊扣學生學習的最近發展區，聯系向量、誘導公式等知識，發展思維的嚴謹性：思路二幾何多于代數，注重對幾何問題的圖形分析，探索解決問題的思路兩個證明思路注重學生的數學思維活動，從數學直觀向理性思維轉變，培養學生的邏輯推理素養。

設計意圖例1、例2、例3三個例題的設置，從具體角到字母角，再到具體角與字母角的混合，幫助學生理解運算對象的變化，重在鞏固基本知識，變1、變2分別將例2、例3的單個角換成復雜角，重在運算思路的探尋，提升基本技能，強化換元等基本思想，例題和變式形成有機整體，培養學生數學運算素養。

2.5作業布置，拓展探究

（1）將課堂探究圖形中角α的余角記為α，請探究有關α與β的等式。

（2）若將兩對斜邊長為1的直角三角形拼成如圖9所示的矩形，請探究圖9中空白部分菱形面積的含義。

（3）（選做）你還能用這些直角三角形拼出其它常見平面圖形，并根據其幾何關系探究代數關系嗎？

設計意圖探究（1）是課堂活動的延伸，探究結果是兩角（銳角）和的正弦公式;探究（2）給出了第三種矩形的拼接方式，根據標注角的不同，探究結果可能是兩角（銳角）差的正弦公式，也可能是兩角（銳角）和的余弦公式，通過探究（1）（2），啟發學生的思維，幫助學生強化基本活動經驗，為其它公式的學習做好鋪墊，培養直觀想象素養，探究（3）在探究（2）的基礎上，具有較大的開放性，旨在培養學生的創新意識。

3教后反思

3.1實踐活動重數學直觀

關于三角公式的學習，學生往往更關注公式的實用性，忽略對三角公式的理解，因此，本節課的教學設計，從整體教學設計理念出發，將三角知識的學習放置于整個初、高中相關知識的學習中，以學生認知發展規律為依據，圍繞幾何圖形構建實踐活動，其中，在創設情境、探究發現和探究作業等教學環節，探究對象的幾何圖形和代數要素不斷變化，強化和豐富了學生的實踐活動經驗，不難發現，每個幾何圖形都體現著相應代數表示的一種幾何意義，有助于學生加深對公式的理解，積累數學實踐活動經驗，有助于學生數學直觀的培養，發展學生發現數學結論的能力和意識，讓學生自然地學習知識。

3.2思維活動重數學推理

不論是證明公式，還是應用公式，都是用已有數學知識解決數學問題的過程，都應幫助學生發展數學思維，因此，對于公式的推廣與證明，教學中不急于陜速完成，而是通過精心設置問題，引導學生積極思考，遵循最近發展區理論，探尋較為自然的證明思路;對于公式的應用，教學中以題組、變式等方式，題目設置由簡至繁，將解題經驗逐步歸一，構建科學思維體系，積累數學思維活動經驗，就要在教學活動中，引導學生將調動基礎知識、施展基本技能、應用基本思想有機融合，積累解決數學問題的經驗，完善認知結構，發展自動自覺的思維意識。

總之，教學中既要關注實踐活動，也要關注思維活動，它們是基本活動的兩個側面，與其它“三基”緊密聯系，教學過程中，注重幫助學生積累基本活動經驗，就能推動學生思考數學問題，發展數學核心素養。