在“說”中“知其行”

鮑瀾瀾

【摘要】曾經有學者對學習和日常生活中信息交流的情況做過統計：聽占45%，說占30%，讀占16%，寫占9%。這說明，聽和說在信息交流中占有比較重要的地位[1]。文章探討了怎樣才能讓學生“想說”“會說”，從而使學生在學習知識的同時，語言、思維也得到同步發展，更好地實現核心素養下的培養目標。

【關鍵詞】說;言語表達;思維能力

著名的心理學家邵瑞珍在其編著的《教育心理學》中指出：“由于言語表達具有重要的提煉功能，所以思想經過語言的精確表達之后，就增加了意義和遷移的可能性。”[2]據此，我們應該把言語表達看作整個思維過程的一個組成部分。為此，在課堂教學中，我們要創造條件讓學生表達，加強對學生說的訓練，在不同課型與各個環節都要加強對學生進行說的訓練，培養學生的口頭表達能力。下面結合具體教學實踐，從計算教學中、概念教學中、解決問題教學規定知識中來談一談如何讓學生在“說”中“知其行”。

一、計算教學中的“說”

計算題，很多學生會做，但不能規范、有條理地說出來。因此，在計算教學中應重視說的過程，這樣既能幫助學生鞏固所學的計算方法，加強算理教學，又能發展學生思維。在計算教學中，應讓學生說算理、說運算順序和說計算方法[3]，并且對于計算中出現的錯誤，要讓學生說出錯誤的原因等，從而有效進行“說”的訓練，培養學生的表達能力。

1.說算理

計算教學的重點是弄清算理，掌握計算法則。學生是否理解算理，掌握算法，那就要看他能否清楚完整地說出來。只有學生說出來，教師才能收到反饋信息，了解學生的掌握情況，而說算理也是學生深入理解、掌握知識的過程。

例如：在教學二年級下冊“三位數加兩位數”時，先出示“85+143=？”讓學生獨立計算，再引導學生說一說這樣算的理由，從而讓學生講清算理。即：由于85是由8個十和5個一組成的，143是由1個百、4個十和3個一組成的，所以先把5個一與3個一相加得8個一;再把8個十與4個十相加得12個十;十位相加滿十要向百位進1，十位上寫2，向百位進1，百位上原來的1加上十位上進上來的1等于2，結果是228。這樣進行說理訓練，學生的思維越來越有條理性，同時加深了對算理的理解。

2.說算法

在交流算法的過程中，要訓練學生清晰而有條理地說出計算方法，加深對所學知識的理解。例如：在教學三年級下冊“兩位數乘兩位數”時，通過情境圖學生知道了這道題要求訂一份牛奶要花多少錢，就是用28×12，然后讓學生獨立進行計算，并引導學生說一說自己是怎樣計算的。生a：可以先求出10個月要多少錢？即10個28是多少，再求2個月要多少錢？即2個28是多少，然后把兩個積加起來。生b：可以用豎式計算，先用2去乘28得56，再用1個十去乘28得到28個十，因此，應把8寫在十位上，2就要寫在百位上，然后把兩次相乘的積相加。讓學生知道在說的過程中，進一步明確計算乘數時兩位數的乘法要分三步走，前兩步乘，第三步相加，這樣讓學生在反復說的過程中，能夠進一步理解與掌握計算方法。

3.說錯因

教學中，教師經常會感慨：這題做過好多次了，為什么還出錯呢？其實，有時苦口婆心的說教，不如讓學生在糾錯中自評自省。例如：在教學四年級下冊“運算律”之后，練習九有這樣一道練習題：294-36+64。很多學生因為受到加法結合律的思維定式影響，寫出294-36+64=294-（36+64）。對此，老師并沒有做出任何評判，而是讓學生自己發表見解。

生1：我覺得可以簡便計算，這種解法是運用了加法結合律。

生2：我認為不可以簡便計算，因為加法結合律都是幾個數連加，而這里是加減混合運算。

生3：（恍然大悟）對，這道題不能簡便，因為是加減混合運算，所以要從左到右依次計算。

師：那怎樣才可以這樣解答呢？

生1：只有是294-36-64時才可以用294-（36+64）解答，剛才我做錯了。

有一位社會心理學家這樣說：“我們期望學生犯錯誤，因為從錯誤中吸取教訓，便可爭取明天的成功。”這樣讓學生說出錯誤的原因，能讓學生更好地理解算理和掌握法則，同時也促進了學生思維的發展。

二、概念教學中的“說”

小學數學概念有其嚴格的科學性，要遵循辯證唯物主義的認識論及符合兒童的認知規律。在概念教學中進行“說”的訓練，是由直觀認識轉化為理性認識，用既準確又概括的數學語言把各種概念、公式、法則和性質等揭示出來。學生只有形成正確、清晰、完整的數學概念，才能掌握好基礎知識。如果學生連概念本質都說不清楚，數學知識就成了“水中月，鏡中花”。因此，訓練數學語言表達能力，讓學生說出概念和概念的關鍵詞，以及說出公式、法則和性質的具體內容，是概念教學的重要過程。

例如：在教學“比的基本性質”這一課時，就要充分利用學生已有知識，精心安排“說一說”的活動，使學生在聯想、猜測、觀察、對比、類推等過程中總結出概念，鞏固和加深所學新知。

師：同學們，你們能說一說比的性質是什么嗎？

生1：比的前項和后項同時乘或除以一個相同的數（0除外），比值不變。

師：那你們能不能舉例論證說一說比的性質呢？

生2：我是這樣論證的，因為4∶6=4÷6=2/3?，而8∶12=8÷12=2/3，所以4∶6=8∶12。從中可以看出，比的前項和后項都擴大了2倍，比值沒有變化。

生3：我是這樣想的，比的前項相當于除法中的被除數，比的后項相當于除數，比值相當于商，由此推斷出比的基本性質。

生4：根據比與分數之間的關系可以知道，比的前項相當于分數中的分子，后項相當于分母，比值相當于分數值。對比分數的性質，可以得出比的基本性質。

師：同學們說得都很好。

在這個教學片斷中，學生根據商不變的性質和分數的基本性質進行大膽探索交流，讓數學課堂更富含“數學味”。因此，在概念教學中重視“說”的訓練，能提升學生的遷移能力和概括歸納能力。

三、解決問題中的“說”

1.說圖意

出示主題圖，讓學生先觀察，然后要求學生說一說看到了什么？編一個小故事，提一個相關的數學問題，促使學生有話可說。

例如，三年級上冊的“找規律”，教材中出示了一張圖片，我們可以讓學生先仔細觀察圖片，再和學生談話：看了這幅圖，誰能編個好聽的故事給大家聽呢？

生：兔媽媽和兔寶寶們住在美麗的大森林里，它們一起游戲，一起學習，手帕臟了，就洗了晾起來，大灰狼來了，它們一起打木樁做陷阱，相親相愛地生活在一起。

學生編完小故事，老師接著問：從圖中你知道了什么？你想提哪些數學問題？

生：兔子曬了多少塊手帕？用了多少個夾子？

生：有幾個蘑菇？有幾只兔子？

生：有多少塊籬笆？有多少根木樁？

……

數學中的“說”具有舉足輕重的作用，讓學生在情境中去發現，去尋找數學問題，成為一個數學問題的發現者，既符合兒童的心理特點，也能調動學生“說”的積極性，讓學生感受到數學就在身邊，從而有效促進學生積極主動地參與到學習活動中，最終達到核心素養下的培養目標。

2.說思路

在解題時，由于學生掌握的知識程度不同，思維發展水平不同，學生會從不同的角度去思考問題，因此在教學“解決問題”時，可讓學生獨立思考，認真分析，說一說解題思路與方法，通過“說”發展思維，疏通思路。

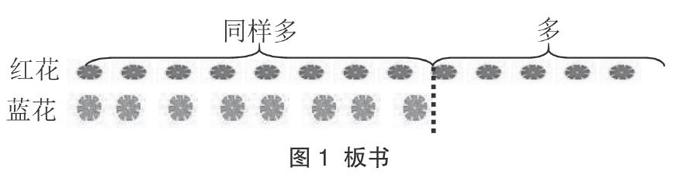
例如，在教學一年級下冊“解決兩數相差多少的實際問題”時，出示：紅花13朵，藍花8朵，紅花比藍花多多少朵？

生1：我是這樣想的，要求紅花比藍花多多少朵，“多”是指紅花的朵數與藍花一個對一個，對完后還多出來的部分就是紅花比藍花多的朵數，所以用減法計算。

生2：我們要求紅花比藍花多幾朵，就可以從13朵紅花里拿掉和藍花同樣多的8朵，剩下的就是紅花比藍花多的5朵，所以用減法計算。

板書形成（圖1）。

課堂中普遍存在一個問題，就是教師將自己的思路直接講給學生聽，而且越到高年級這種現象就越嚴重，導致學生對解題思路還停留在一知半解中。所以，在解決問題教學時，先讓學生獨立思考，明確題中的數量關系，說一說解題思路，從“說”中發展智力，以說促思，讓學生真正理解所學知識，體驗成功的愉悅。

四、規定知識中的“說”

學生的數學學習從某種意義上說，是一種體驗，正所謂“手腦并用聽說寫，心中悟出始知深”[4]。在規定知識教學中，往往都是老師講、學生聽，結果一節課下來，老師講得口干舌燥，學生聽得云里霧里。這就更需要讓學生來說一說，便于學生觀察規律、發現規律和掌握規律。

例如，三年級下冊的“年月日”第二課時“平年閏年”的教學，教師先出示2005年至2016年的2月份月歷卡。

師：觀察月歷卡，根據每年二月的天數，找一找，哪些年份是平年？哪些年份是閏年？并在年份的旁邊用“平”或“閏”標出來。

學生自主判斷，教師巡視指導，指名匯報。

根據學生的匯報，教師板書（圖2）。

師：從2005年開始，大家讀一讀平年和閏年的排列，說說有沒有什么規律呢？

學生讀著讀著，不一會兒全班學生就都有節奏地齊聲讀出來。

師：誰來說一說，有什么規律呢？

生1：平平平閏? ? 平平平閏? ? 平平平閏

生2：它們是按“平平平閏”四個為一周期依次不斷重復出現。

（教師板書圈出：平平平閏）

“語言是思維的外殼”，讓學生以讀助找，并說一說規律，抓住了以上關系，就抓住了本質，不管題目怎么變化，都可以以不變應萬變。當學生能按照“平平平閏，平平平閏……”這樣每四字一頓、有節奏地說出來時，就充分說明學生已經發現了平年和閏年的排列規律，為以后的學習打下了良好的基礎。

總之，在課堂教學中，要注重讓學生張開嘴巴“說”，激發學生“說”的興趣，挖掘學生“說”的動力，使他們想說、愛說、會說，經歷獲取知識的思維過程，把教學建構在核心素養的培養上，讓數學課有一定的“深度”與“厚度”。

【參考文獻】

肖紅梅.精心培養一年級孩子傾聽的良好習慣[J].發現，2018（13）：8.

邵瑞珍.教育心理學[M].北京：高等教育出版社，1999.

陳華忠.加強“說”的訓練，培養表達能力[J].小學教學設計， 2014（02）：7-9.

張秀琴.體驗，展現數學的魅力[J]. 理科愛好者（教育教學版），2009，1（01）：96.