基于二維模型預(yù)測控制的迭代學(xué)習(xí)控制性能評估方法
王永耀,索寒生,王 娟,孫希法
(1.中國石油化工集團有限公司 信息和數(shù)字化管理部,北京 100728;2.石化盈科信息技術(shù)有限責(zé)任公司 信息技術(shù)研究院,北京 100007;3.北京化工大學(xué) 信息技術(shù)研究院,北京 100029;4.北京時代凌宇科技股份有限公司,北京 100012)
為實現(xiàn)工業(yè)生產(chǎn)中的批次過程更好地運行,研究人員在批次生產(chǎn)控制方面做了大量的研究工作,迭代學(xué)習(xí)控制(iterative learning control,ILC)能夠充分挖掘重復(fù)信息,是處理批次過程的有力工具。由于缺乏足夠的維護、設(shè)備老化、傳感器/執(zhí)行器故障等原因[1],控制器的性能會隨著時間的推移逐漸下降,監(jiān)測和評定控制器性能的性能評估技術(shù)應(yīng)運而生[2]。然而,針對迭代學(xué)習(xí)控制的性能評估研究不多;同時,由于批次過程的周期性或重復(fù)性,針對一般系統(tǒng)的性能評估方法不適用。因此,迭代學(xué)習(xí)控制性能評估研究對推動工業(yè)發(fā)展具有重要意義。
1978年,迭代學(xué)習(xí)控制的概念首次出現(xiàn)在文獻[3]中。1984年,Arimoto等[4]首次發(fā)表了ILC方面的研究論文。1990年,Geng等[5]成功地將二維系統(tǒng)理論應(yīng)用于離散系統(tǒng)的迭代學(xué)習(xí)控制的設(shè)計,在此之后大批學(xué)者參照這個思路進行了研究[6]。二維系統(tǒng)是能夠同時在兩個獨立的方向上演化的動態(tài)系統(tǒng)[7],考慮到迭代學(xué)習(xí)控制的更新恰好同時包括時間軸和批次軸,因此可以把迭代學(xué)習(xí)控制作用下的閉環(huán)系統(tǒng)轉(zhuǎn)換成二維系統(tǒng),從而達到簡化研究的效果。
控制性能評估(control performance assessment,CPA)技術(shù)可以有效解決控制性能欠佳的問題,因而在學(xué)術(shù)界和工業(yè)界引起廣泛的關(guān)注[8]。控制性能評估的相關(guān)研究最早可以追溯到1970年[9]。1989年,Harris在最小方差控制的背景下引出名詞性能指標(Harris指標)[10],象征著CPA的興起。大批學(xué)者致力于拓展此領(lǐng)域,并取得了突破性進展。Huang等[11]為簡化最小方差基準計算,提出使用濾波相關(guān)法進行估計。最小方差基準由于過于理想化,其他更貼近實際的性能評估基準被陸續(xù)地設(shè)計出來。Huang等[12]基于線性二次高斯控制器設(shè)計了線性二次高斯(linear quadratic Gaussian,LQG)基準——展現(xiàn)為一條性能權(quán)衡曲線,LQG基準比最小方差控制(minimum variance control,MVC)基準更貼近實際。Zhao等[13]將LQG基準應(yīng)用到先進過程控制的經(jīng)濟性能評估。Julien等[14]提出了模型預(yù)測控制(model predictive control,MPC)基準,已在工業(yè)界有很多成功的應(yīng)用案例,是目前最實用的先進控制方法。
雖然性能評估技術(shù)成果頗豐,但有關(guān)迭代學(xué)習(xí)控制的評估研究報道較少。直到2009年,Chen和Kong的工作[15]彌補了這一缺憾,以最小方差控制為基準對ILC進行性能評估。2013年,F(xiàn)arasat和Huang指出文獻[16]遺漏了確定性性能與隨機性性能之間的耦合關(guān)系,通過把系統(tǒng)劃分為內(nèi)環(huán)控制器和外環(huán)控制器,同時加入權(quán)重系數(shù),提出了一個更全面的方案。2015 年,Wei等[17]選用線性二次高斯基準構(gòu)建了一個全新的評估工具——性能評估曲面。接著,Wang等[18]繼續(xù)對該理論進行深入研究,進一步將一維基準控制器改進為二維基準控制器。隨著迭代學(xué)習(xí)控制在工業(yè)過程中的地位越來越重要,亟需更好的框架來評估其性能。
本研究利用二維系統(tǒng)理論,首次為迭代學(xué)習(xí)控制設(shè)計MPC基準的性能評估策略。針對工業(yè)過程通常模型未知的問題,設(shè)計了閉環(huán)子空間辨識方法,進而得到數(shù)據(jù)驅(qū)動的評估策略。算法可以概括為:根據(jù)測量得到的輸入輸出數(shù)據(jù)構(gòu)造Hankel矩陣,再借助正交三角分解(QR decomposition,QRD)、奇異值分解(singular value decomposition,SVD)等幾何工具計算出子空間矩陣[19],由列子空間與行子空間估計出系統(tǒng)模型參數(shù)。在得到辨識模型后,把迭代學(xué)習(xí)控制作用下的閉環(huán)系統(tǒng)轉(zhuǎn)換成二維模型,進而設(shè)計基于二維MPC基準的控制性能評估策略。設(shè)計方法在注塑過程上進行了仿真測試。
本研究的主要創(chuàng)新在于:為迭代學(xué)習(xí)控制設(shè)計了二維MPC基準的性能評估策略;針對工業(yè)過程通常模型未知的問題,首次設(shè)計了數(shù)據(jù)驅(qū)動的評估策略;對Fornasini-Marchesini(FM)模型參數(shù)的獲取進行了深入研究。
1 子空間辨識
漢克爾矩陣(Hankel matrix):

托普利茲矩陣(Toeplitz matrix):

由于子空間辨識是基于投影的算法,接下來將介紹其中涉及到的正交投影理論:
任意矩陣的行空間映射至矩陣Φ的行空間上的算子記為:
∏Φ=ΦT(ΦΦT)?Φ,
(1)
其中,符號?代指偽逆,在MATLAB中,調(diào)用函數(shù)pinv即可求得。
在此基礎(chǔ)上,可以得到Ψ/Φ=Ψ∏Φ=ΨΦT(ΦΦT)?Φ。
類似地,任意矩陣的行空間映射至矩陣Φ的行空間正交補上的算子記為:
∏Φ⊥=Ι-∏Φ,
(2)
則有
Ψ/Φ⊥=Ψ∏Φ⊥。
借助∏Φ和∏Φ⊥,能夠把Ψ拆分為下列形式:
Ψ=Ψ∏Φ+Ψ∏Φ⊥。
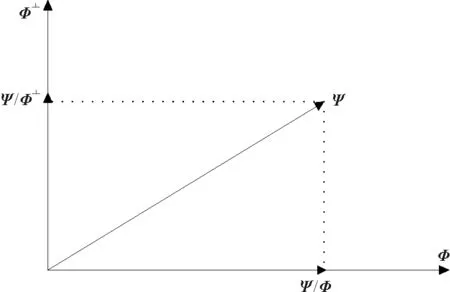
圖1 矩陣正交投影過程的圖像化展示
如圖1所示。
2 二維子空間矩陣
考慮如下批次過程:
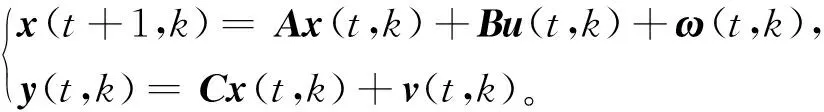
(3)
其中,t=0,1,…,T-1,為時間指標;k=0,1,…,N-1為批次指標;x∈Rn、u∈Rp以及y∈Rm分別表示狀態(tài)、輸入和輸出;ω∈Rn與v∈Rm皆為高斯白噪聲,分別指系統(tǒng)噪聲、測量噪聲。
對于上述批次過程,引入如下形式的迭代學(xué)習(xí)控制律:
∑ILC:u(t,k)=u(t,k-1)+r(t,k)。
(4)
其中,r(t,k)是待設(shè)計的學(xué)習(xí)律。
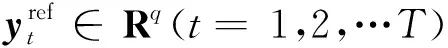
(5)
為了在二維系統(tǒng)理論框架下進行推導(dǎo),定義符號:
(6)
由式(3)~(6),可以得到如下所示的二維系統(tǒng)的典型描述形式——Fornasini-Marchesini(FM)模型:
(7)
(8)
把式(7)簡化成:
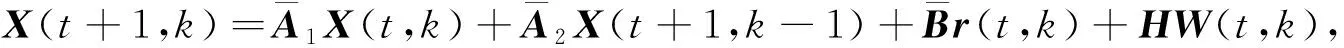
(9)
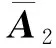
(10)
又注意到A1第二列矩陣塊的元素都為0,所以作下列變形也不會造成影響:
(11)
考慮下列新息模型,可以看出是對式(11)的一般化形式:
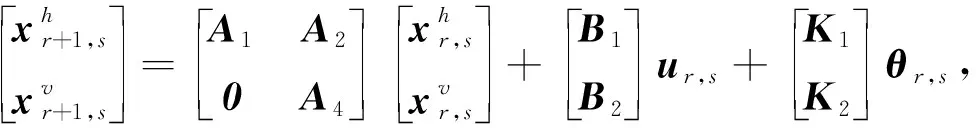
(12)
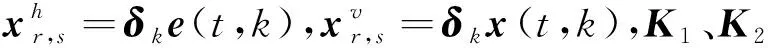
根據(jù)Ramos等學(xué)者的理論,對式(12)進行反復(fù)的迭代操作,最終獲得下述子空間等式:
(13)
(14)
(15)
其中,下標p指過去項、f指未來項,輸入Hankel矩陣Up和Uf定義如下:
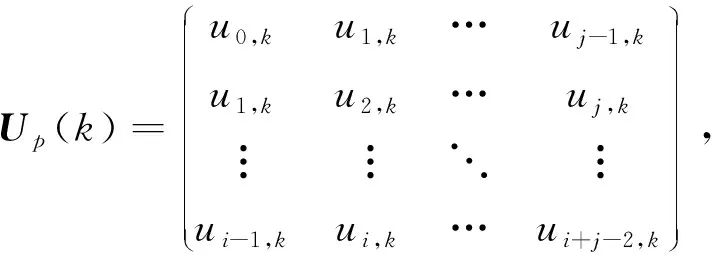
輸出Hankel 矩陣的具體表達式為:

狀態(tài)矩陣定義如下:
擴展的可觀測矩陣以及擴展的可控矩陣的具體表達式分別為:
下三角托普利茲矩陣為:
上述過程是為閉環(huán)子空間辨識做準備,下一節(jié)借鑒文獻[20]的子空間模型辨識主元分析(subspace model identification-principal component analysis,SIM-PCA)思想,面向開環(huán)系統(tǒng)的二維子空間辨識,推導(dǎo)出帶有擾動閉環(huán)的方法。
3 閉環(huán)子空間辨識
(16)
接著,做一些簡單的變形:
(17)
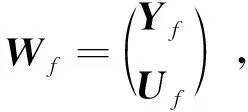
(18)

(19)
(20)
(21)
記Z=Wf/Wp,對Z做SVD分解:
(22)
結(jié)合式(21)和式(22),可以看出Z的正交列空間等于U2,則有
(23)
其中,M可以取作任意的常數(shù)非奇異矩陣。
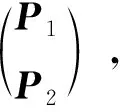
(24)
由式(24)可以得到:
(25)
(26)
4 控制性能評估
根據(jù)第3節(jié)中的算法,可以獲得系統(tǒng)矩陣A、B、C、D,進而得到系統(tǒng)(9)。為該二維系統(tǒng)設(shè)計控制器:
r(t,k)=K1X(t,k)+K2X(t+1,k-1)。
(27)
實際上,這種情況下的二維控制器設(shè)計可以分解為狀態(tài)反饋控制和前饋ILC控制。狀態(tài)反饋控制用來提高系統(tǒng)狀態(tài)的收斂性能,而前饋ILC控制則用于保證沿批次方向的收斂性。
結(jié)合式(9)和式(27),可以得到以下形式:
(28)
定義二維MPC代價函數(shù):
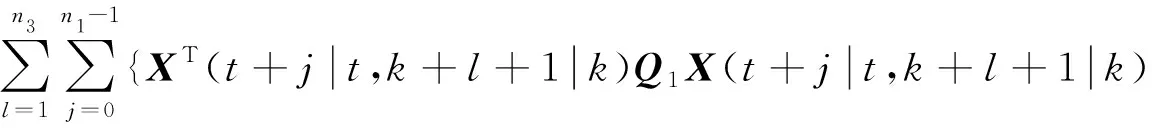
+XT(t+j+1|t,k+l|k)Q2X(t+j+1|t,k+l|k)
+(r(t+j,k+l+1))TMr(t+j,k+l+1)}}
(29)
其中,φT(j,l)=[XT(t+j|t,k+l+1|k),XT(t+j+1|t,k+l|k)],Q1,Q2,M是權(quán)重矩陣。
MPC基準控制器可以通過求解下列優(yōu)化問題獲得
(30)
但一維MPC控制問題的解決方案不能直接應(yīng)用于二維系統(tǒng),因為兩個系統(tǒng)的結(jié)構(gòu)和動態(tài)復(fù)雜性有著顯著的差別。為此,本節(jié)提出了一個次優(yōu)的解決方案。在證明主要結(jié)論的過程中,需要用到下面兩個引理。
引理1[21]對于具有適當(dāng)維度的給定矩陣W,L和V,其中W和V是正定矩陣,滿足
LTVL-W<0。
(31)
當(dāng)且僅當(dāng)
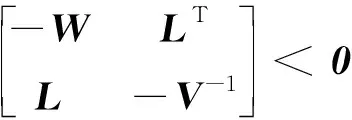
(32)
引理2[22]設(shè)E、G、F和M表示具有適當(dāng)維度的實矩陣,M滿足M=MT,則對于所有GTG≤I,
M+EGF+FTGTET<0,
(33)
當(dāng)且僅當(dāng)存在μ>0滿足
M+μ-1EET+μFTF<0。
(34)
定理1假設(shè)W(t,k)≡0成立。給定二維FM系統(tǒng)(9),則優(yōu)化問題(30)是可解的,如果存在正定對稱矩陣S1、S2、Ω以及矩陣Y1、Y2,滿足
(35)
基于上述線性矩陣不等式(linear matrix inequality,LMI)的解,可以得到控制律的增益:
K1=Y1Ω-1,K2=Y2Ω-1。
(36)
證明:設(shè)計如下Lyapunov函數(shù):
(37)
其中,[·]是任何具有適當(dāng)維度的正定對稱矩陣。對于正定對稱矩陣P、R1、R2,有
ΔV(X(t,k))=Vp(X(t+1,k))-VR1(X(t,k))-VR2(X(t+1,k-1))
=‖X(t+1,k)‖p-‖X(t,k)‖R1-‖X(t+1,k-1)‖R2。
(38)
根據(jù)等式(28),可以得到:
(39)
對式(35)的左側(cè)矩陣分別左乘和右乘對角矩陣diag{P,P,I,I,I,I},得到矩陣不等式(35)等價于
(40)
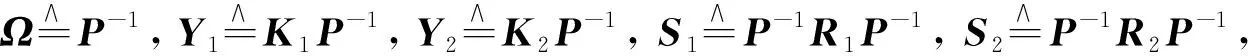
(41)
由此,可以得到
(42)
根據(jù)上式有:
(43)

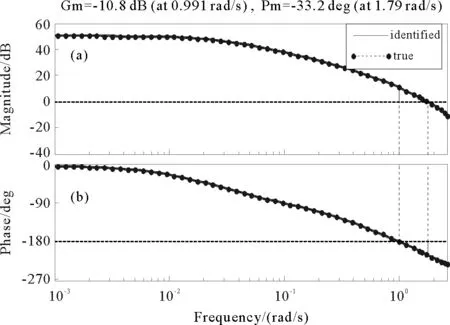
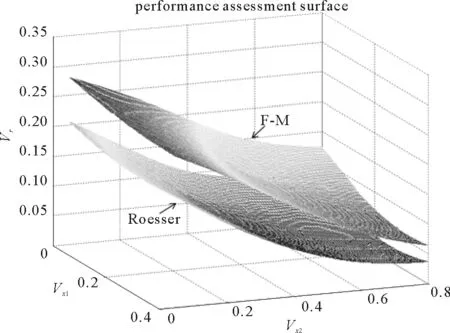
Vp(X(t+1,k)) (44) 不失一般性,假設(shè)R1=λP,R2=(1-λ)P,也就是說R1=P-R2,這帶來 Vp(X(t+1,k)) (45) 對于任意整數(shù)T0,K0,i>0,以下不等式成立: Vp(X(T0+1,K0+i)) Vp(X(T0+2,K0+i-1)) +VR2(X(T0+2,K0+i-2), ? Vp(X(T0+i,K0+1)) +VR2(X(T0+i,K0)。 把這些不等式相加,得到 很明顯,Lyapunov函數(shù)值的總和沿狀態(tài)軌跡逐漸減小,那么當(dāng)系統(tǒng)批次趨向于無窮時,會完全跟蹤期望軌跡。 證明完畢。 注塑成型是典型的批次過程,其注射階段對注射速度的控制關(guān)乎產(chǎn)品質(zhì)量的高低。本節(jié)選用注塑過程的注射階段作為研究對象,通過仿真實驗來驗證設(shè)計的算法。 已經(jīng)確定相對于比例閥的注射速度被描述為如下模型[23]: (46) 上述傳遞函數(shù)模型可以轉(zhuǎn)換成下列狀態(tài)空間模型: (47) 在仿真中,首先假設(shè)模型參數(shù)是未知的,使用上述模型生成的數(shù)據(jù)來驗證所提出的閉環(huán)子空間辨識方法。為此,進行了30次仿真實驗,并從不同角度展示了識別結(jié)果。 圖2 系統(tǒng)矩陣A的特征根 圖3 真實模型和識別模型的波德圖 表1 特征值的平均值和方差 圖2描述了系統(tǒng)矩陣A的真實特征根和利用子空間算法識別出的特征根,經(jīng)過對比可知辨識效果較為理想。同時,表1中的數(shù)據(jù)也表明,特征根的平均值和方差皆處于可接受的范圍內(nèi)。圖3是真實模型和辨識模型的Bode圖比較。綜上所述,所識別的效果實現(xiàn)了一致的估計和良好的準確性。從而,可以進行下一步的性能評估研究。 該系統(tǒng)的控制目標是跟蹤以下參考軌跡: (48) LQG基準對應(yīng)的代價函數(shù)通常選取: (49) 根據(jù)已有的求解LQG問題的算法,就可以得到r(t,k)的最優(yōu)解;然后就能夠擬合出性能曲面。為了對比兩種基準的評估效果,將它們分別作為評估模型(47)的基準,并將各自的性能曲面展示在同一個仿真圖(圖4)中。 由圖4可看出,MPC基準對應(yīng)的性能曲面要高于LQG基準對應(yīng)的性能曲面。造成這種局面的原因有兩個:第一,過程模型的精確度不能百分百保證,在設(shè)計模型預(yù)測控制器時經(jīng)常采用與實際模型不匹配的近似模型。第二,兩者優(yōu)化目標中的時間范圍不同:MPC的優(yōu)化目標是有限時域,而LQG是無限時域。因此,即使過程和擾動模型精確已知,MPC性能曲面也一定高于LQG性能曲面。 圖4 兩種基準下的性能曲面比較 本研究提出一種基于二維模型預(yù)測控制的迭代學(xué)習(xí)控制性能評估方法。考慮到實際的工業(yè)過程中通常無法知曉系統(tǒng)的模型,對如何獲取FM模型參數(shù)展開了研究。為了保證安全、產(chǎn)品質(zhì)量、系統(tǒng)穩(wěn)定運行等,只能在閉環(huán)條件下進行辨識,由此提出了子空間辨識算法,所識別的效果實現(xiàn)了一致的估計和良好的準確性。在得到辨識模型后,把迭代學(xué)習(xí)控制作用下的閉環(huán)系統(tǒng)轉(zhuǎn)換成二維模型,進而設(shè)計基于二維MPC基準的控制性能評估策略,其性能曲線高于LQG基準曲線。算法的仿真測試結(jié)果驗證了其有效性。5 仿真實例
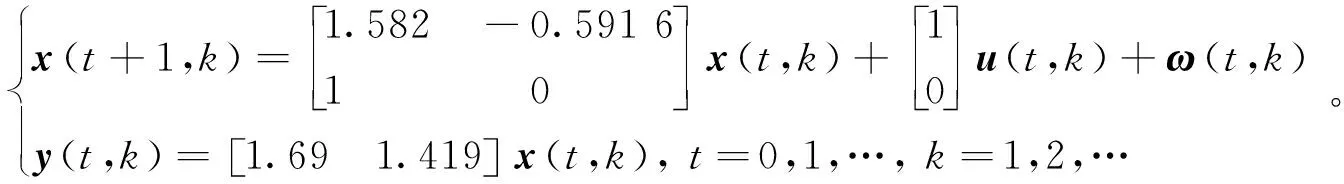


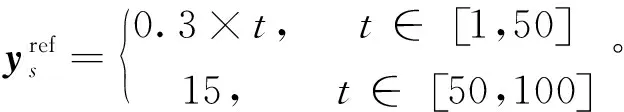
6 結(jié)論

