基于APOS理論下的小學數學概念教學的研究

劉祥

[摘要]美國著名數學教育家杜賓斯基提出的APOS理論把數學概念教學分為四個階段：活動階段、過程階段、對象階段、圖式階段。以小學數學中的“分數的初步認識”教學內容為例，以APOS理論為基礎，借助多媒體軟件設計概念教學的四個階段。通過創設真實的活動情境，使學生感悟分數;開展小組合作探究，使學生理解“分數”的概念;建構對象實體，促學生把握“分數”的本質;建立深層圖式，助學生形成概念的基本體系。

[關鍵詞]APOS理論;概念教學;分數

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2020）11-0022-03

一、問題提出

美國的數學家杜賓斯基提出的APOS的理論認為，作為學習者不能直接學習到數學的概念，而是要通過一些心智結構使得所學的概念產生實際的意義，教學的真正目的是要幫助學習者建立合適的心智結構。APOS理論以活動、過程、對象與圖式四個具體的階段體現了數學概念的形成與思維過程。

執教教師以APOS理論為指導，借助多媒體演示動態生成的全過程來設計概念教學過程的四個階段，有助于學生學習“分數的初步認識”中的概念。

二、APOS理論的概念教學階段與多媒體的運用

杜賓斯基認為，任何一個數學教育中的理論或模型都應該致力于對“學生是如何學習數學的”以及“什么樣的教學計劃可以幫助這種學習”的理解，而不僅僅是陳述一些事實。正是基于這樣的考慮，杜賓斯基建立了APOS理論，而APOS理論中包含四個基本的階段：

1.活動（Action）階段

“活動階段”是指個體或學習者通過一步一步的外顯性（或記憶性）指令去變換一個客觀的數學對象，它是學習者獲得數學概念不可缺失的條件。在小學數學中，許多的概念都是“隱性”的，需要通過一些外顯的探究活動去獲得概念的本質。在數學概念的教學中，借助多媒體教學，能夠將教學的對象動態地呈現在學生面前，通過有效操作，產生良好的教學效果，從而讓學生感悟“分數”的本質，由此能夠獲得概念的表象。

2.過程（Process）階段

“過程階段”是外顯數學的活動思考的過程，當“活動”經過多次的重復而被個體熟悉后，就可以內化為一種稱之為“過程”的心理操作。有了這種“過程”，個體就可以想象這個“活動”，而不需要通過外部的刺激;他可以在頭腦中實施這個過程，而不需要具體操作;進而，他還可以對這個過程進行逆轉以及與其他程序進行組合。學生多次重復和熟悉之后，就能進行一系列的心理活動，抽象出數學概念的本質屬性。在數學概念的獲得中，可以借助多媒體將數學的對象轉化為動態圖像，通過演示幫助學生從圖形中發現“分數”的本質。

3.對象（Object）階段

當個體或學習者能夠把“過程”作為一個整體進行操作時，這一過程就變成了一種心理“對象”。借助多媒體將概念的對象做一系列的動態操作演示，就能幫助學生把握概念的特點及性質，深層次認識概念。

4.圖式（Scheme）階段

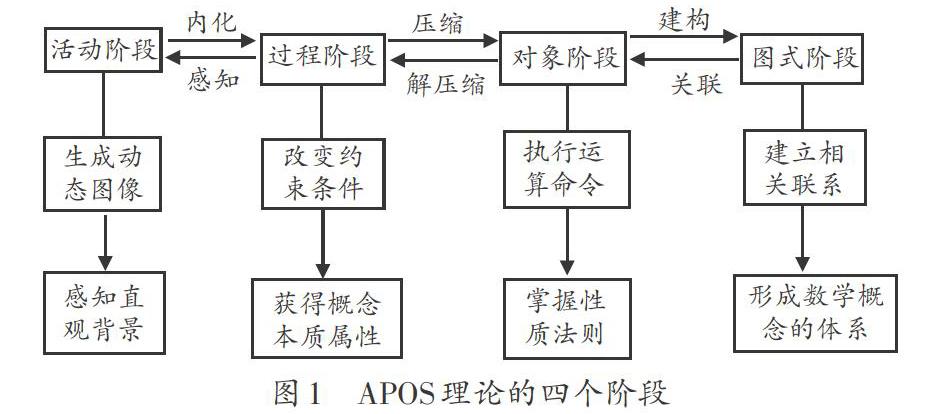
一個數學概念的“圖式”是指由相應的“活動”、“過程”、“對象”以及與某些一般原理相聯系的其他“圖式”所形成的一種個體頭腦中的認知框架，它可以用于解決與這個概念相關的問題。從這個意義上看，APOS理論中的“圖式”有點類似于韜爾的“概念意向”。以上四個階段及其關系如圖1所示：

按照杜賓斯基的解釋，上述四個成分中，“活動”、“過程”和“對象”也可以看作是數學知識的三種狀態，而“圖式”則是由這三種知識結構構成的一種認知結構。此外，上述四種結構成分的排列雖然在理論上具有一種等級結構，也就是說，一般情況下前一成分的建構是后一成分的基礎。APOS理論認為，在數學學習中，在恰當引導前三個階段后，學習者本身在建構與反思的基礎上能夠形成圖式，進而厘清問題的情境，獲得數學概念的本質。本文以俞正強老師教學的“分數的初步認識”為例，以APOS理論為指導，借助多媒體探索小學數學概念教學的過程。

三、分數的初步認識概念教學設計

1.創設真實的活動情境，初步認識“分數”

依據《義務教育數學課程標準（2011年版）》，學生在學習分數之前，對分數并不了解，也不知道怎么讀與寫，所以在引入分數的概念之前，俞老師并沒有直接給出分數的概念，而是通過創設具體的情境，使得學生逐漸體會整數與分數，慢慢抽象出分數的概念。

師：大家吃過月餅嗎？

生（齊）：吃過。

師：請看大屏幕。今天老師帶來一些月餅，這是幾個月餅呢？

生1：一個。

師：老師又帶來這樣的月餅，你們猜猜看是多少呢？

生2：半個。

生3：半個。

師：你們太聰明了。

根據APOS理論，在最初的活動階段，學習者通過一步一步的外顯性（或記憶性）指令去變換一個客觀的數學對象，它是學習者獲得數學概念不可缺失的條件。通過有趣的對話活動，教師慢慢喚醒學生對分數的認知，了解學生已有的知識與經驗。通過創設一個月餅到半個月餅的情境，引發學生學習數學的興趣，并逐漸抽象出數字“1”和“半個”（該怎么表示呢？），激起學生學習分數的熱情，為進入APOS的下一個階段做好準備。

2.開展小組合作探究，理解“分數”的概念

師：“半個”月餅用哪個數字來表示呢？請開展小組合作探究。

師：在學習“半個”月餅用哪個數字表示之前，思考一下，這半個月餅是從哪里得來的？

（大屏幕演示“一個月餅”到“半個”月餅的動畫）

生1：半個月餅是從一個月餅里得來的。

生2：半個月餅是把一個月餅分成了“兩半”。

生3：把一個月餅“平均”分成了“兩半”，那么半個月餅就出現了。

師：是的。把一個月餅平均分成了兩塊，取出其中的一塊。平均分成兩塊，在數學里我們用數字“2”表示;取出其中的一塊，我們用數字“1”表示;平均分，用一短橫進行表示。因此我們用“1/2來表示這個“半個”。

師：這個數怎么讀呢？

生4：二分之一。

根據APOS理論，在這一階段，學習者需要對數學活動做進一步的思考。教師借助多媒體動畫演示，通過操作由“一個月餅”到“半個”月餅的形成過程，讓學生通過觀察、比較、分析、歸納等一系列的探究過程，概括出數的特點。在整個APOS的第二個過程中，讓學生對這樣的“數”有了初步的感覺。

3.建構對象實體，把握“分數”的本質

在多媒體技術的支撐下，俞老師列舉多個分數的實例，使學生可以從不同的角度去逐漸體會并建構“分數”的概念，經歷由一個月餅到半個月餅再到1/3個月餅，最后到1/4個月餅，由特殊的“1”到一般的分數的建構過程，很好地抽象出分數概念的本質特征：分數就是把“一個”單位“1”平均分成若干份，其中的每一份可以用分數表示。俞老師幫助學生建構“分數”的概念之后，又幫助學生了解了“分數”具體的量和“分量”的區別。

師：半個月餅可以用哪個數字來表示？

生1.1/2

師：“1/2”和“1/2個”有什么區別和聯系呢？

生2：單獨的1/2表示的是“把一個整體平均分成兩份，其中的一份就用1/2表示。

生3：“1/2個”表示一個物體的一半，是具體的數

量。例如媽媽給我一個蘋果，我吃了這個蘋果的半個，也就是1/2個。

根據APOS理論，教學該階段的目的是要幫助學生抽象出分數概念的本質特征，實現對分數概念的更深層次的認識和理解。在多媒體輔助教學的環境下，俞老師利用多媒體展現從多個動態的實例中抽象出分數的本質概念，讓學生更直觀地看到分數的產生與變化的全部過程。分數的概念具有運算的規則“實體”，即對象。學生學習了分數的概念之后，從“過程”階段進入了“對象”階段，這里，“對象”階段發揮了多媒體的優勢，突出了分數教學的重點，提升了課堂的教學效率，吸引了學生學習分數的熱情與興趣。

4.建立深層圖式，形成概念的基本體系

根據APOS理論，圖式階段是建立概念聯系的階段，即學習者能夠建立新的知識結構，形成新的概念體系。多媒體可以直接呈現分數的產生與變化的過程，能夠引導學生對分數的認識更深入。

師：吃了半個月餅后，還剩幾個月餅？

生1：還剩半個，因為是把一個月餅平均分成了兩半，吃了一半，所以還剩一半。

師：如果把一個月餅平均分成三塊，吃了其中的一塊，還剩多少？

生2：還剩三分之二個，因為是把一個月餅平均分成三份，只吃掉了其中的一份，還剩下兩份，所以剩下的部分占整體的三分之二，即可以用三分之二表示。

人教版教材三年級下冊創設了兩位學生分月餅的情境，由“簡單的一個月餅怎樣才能夠分給兩個學生吃呢？”引發學生思考后得出半個可以用分數表示，符合學生的認知規律，學生比較容易得出分數的概念。

從以上教學可以看出，多媒體能夠幫助學生發現知識的內在聯系，建立深層次的圖式，逐漸建立分數的概念體系。在數學課堂教學中，APOS的四個階段是緊密相連、環環相扣的，在相互作用的條件下完成了對分數概念的建構，讓學生對分數的概念理解得更深刻。

四、思考

本節課是“分數的初步認識”第一節課，分數對于學生來說是比較陌生的，在課堂中幫助學生建構分數的概念就十分關鍵。俞老師的這節課恰恰是基于學生已有的生活經驗，讓學生逐步理解分數的概念。首先，創設真實的活動情境，讓學生初步認識分數;接著，讓學生合作探究，說一說自己對分數的看法;緊接著，讓學生建構對象的實體，理解分數的本質;最后，讓學生建立深層圖示形成分數的概念體系。整堂課設計非常巧妙（感知分數——建構分數的概念——理解分數的概念），貼近學生的實際生活，抓住學生的心理特征，讓學生在愉快的氛圍中去學習并掌握分數的概念，這正體現了“教師是學生的組織者、引導者與合作者，學生是學習的主體”，把課堂還給學生，讓學生用數學的思維去思考現實的世界，用數學的語言表達現實的世界，用數學的眼光觀察現實的世界。

從數學學習心理學角度看，APOS的理論是合理的，反映了學生學習數學概念過程中真實的思維活動。據了解，該理論主要應用于大學數學教學的研究，但也同樣適用于小學數學的概念教學，特別是與多媒體信息技術相結合的情況下，能夠很好地突破學生的認知水平，令課堂教學取得意想不到的效果。

[參考文獻]

[1]鮑建生，周超.數學學習的心理基礎與過程[M].上海：上海教育出版社，2009.

[2]喬連全.APOS：-種建構主義的數學學習理論[J].全球教育展望，2001（3）：16-18.

（責編金鈴）