Gaschütz定理的一個新證明

王兆權(quán)

青島濱海學院文理基礎(chǔ)學院， 山東 青島 266000

[x,y;f]=f(y)-1f(x)-1f(xy)

[x,y;f]∶=f(x)-1f(y)-1f(xy)

稱[x,y;f]為元素x和y的f-反分配子.本文在文獻[5]的基礎(chǔ)上，通過考慮群在函數(shù)集合上的反作用證明了下面的定理.

定理A(Gaschütz定理)設(shè)H是G的交換正規(guī)子群，U是G的子群且滿足H≤U，(|H|,|G/U|)=1.

(1)若H在U中有補群，則H在G中存在補群；

(2)若K1,K2是H在G中的兩個補群，且滿足K1∩U=K2∩U，則H在G中的任意兩個補群共軛.

當U=H時，得到定理A的直接推論：

推論B(Schur-Zassenhus定理)設(shè)H是G的交換正規(guī)子群，且(|H|,|G/H|)=1，則

(1)H在G中有補群；

(2)H在G中的任意兩個補群都共軛.

推論C 設(shè)H是G的正規(guī)子群，如果(|H/H′|,|G/H|)=1，則

(1)H在G中存在關(guān)于H′的相關(guān)補群；

(2)H在G中關(guān)于H′的任意兩個相關(guān)補群共軛.

本文中，其他術(shù)語和符號是標準的，參見文獻[6，7].

1 預(yù)備知識

fa(x)∶=f(a)-1f(xa) ?x∈G

稱fa為函數(shù)f在a下的反共軛.

(1)f(e)=e,其中e為單位元；

(2)f(xy)=f(y)f(x)，?x,y∈G.

則稱f是群G到群K上的反同態(tài).

定義3 設(shè)G是有限群，Map(G,K)為群G到群K上的函數(shù)集合，SMap(G,K)表示集合Map(G,K)的置換群，如果存在一個反同態(tài)映射

則稱群G反作用在集合Map(G,K)上.

證明 先證充分性.對任意g∈G,我們有fx(g)=f(x)-1f(gx)=f(g),即f(gx)=f(x)f(g),所以f是群反同態(tài)；下證必要性.因為f是群反同態(tài),所以f(gx)=f(x)f(g),從而推出fx(g)=f(x)-1f(gx)=f(g).

[x,y;f]∶=f(x)-1f(y)-1f(xy)

稱[x,y;f]為元素x和y的f-反分配子；若引入函數(shù)反共軛，則上述形式變?yōu)?/p>

[x,y;f]=f(x)-1fy(x)

[y,z;f]f(x)=[x,y;f][xy,z;f][x,yz;f]-1

證明 由定義4知,對于x,y,z∈G,一方面有

f(xyz)=f(yz)f(x)[x,yz;f]=f(z)f(y)[y,z;f]f(x)[x,yz;f]

另一方面有

f(xyz)=f(z)f(xy)[xy,z;f]=f(z)f(y)f(x)[x,y;f][xy,z;f]

于是

[y,z;f]f(x)=[x,y;f][xy,z;f][x,yz;f]-1

(2)[x,y；fi·fj]=fj(x)-1fi(x)-1fj(y)-1fi(x)[x,y;fi]fj(y)fj(x)[x,y;fj].

證明 根據(jù)定義1展開得到

(fi·fj)a(x)=fi·fj(a)-1fi·fj(xa)=fj(a)-1·fi(a)-1fi(xa)·fj(xa)

由定義4可得

[x,y；fi·fj]=fi·fj(x)-1fi·fj(y)-1fi·fj(xy)

=fj(x)-1·fi(x)-1fj(y)-1·fi(y)-1fi(xy)·fj(xy)

又注意到f(xy)=f(y)f(x)[x,y;f],于是

[x,y；fi·fj]=fj(x)-1fi(x)-1fj(y)-1fi(y)-1fi(y)fi(x)[x,y；fi]fj(y)fj(x)[x,y；fj]

從而

[x,y；fi·fj]=fj(x)-1fi(x)-1fj(y)-1fi(x)[x,y；fi]fj(y)fj(x)[x,y；fj]

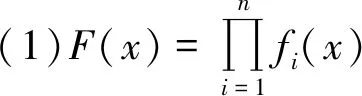
證明 顯然F是群G到群K上的函數(shù).

當n=1時,顯然有[x,y;F]=[x,y;f1]；

當n=2時,通過引理3的結(jié)果(2)得到,

[x,y;f1·f2]=f2(x)-1f1(x)-1f2(y)-1f1(x)[x,y;f1]f2(y)f2(x)[x,y;f2]

又因K是交換群,所以有[x,y;f1·f2]=[x,y;f1][x,y;f2]；

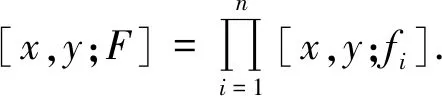
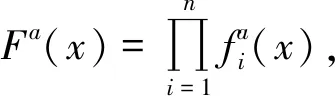
2 主要的證明

定理1(Gaschütz定理)[9,10]設(shè)H是G的交換正規(guī)子群，U是G的子群且滿足H≤U，(|H|，|G/U|)=1.

(1)若H在U中有補群，則H在G中存在補群；

(2)若K1,K2是H在G中的兩個補群，且滿足K1∩U=K2∩U，則H在G中的任意兩個補群共軛.

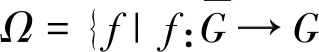
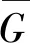
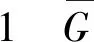
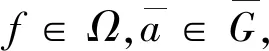
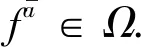
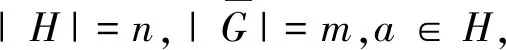
因為H在U中有補群，所以(|H|,|U/H|)=1；又已知(|H|,|G/U|)=1，故可得到(|H|,|G/H|)=1，即(m,n)=1.這樣一定存在整數(shù)k,t使得km-tn=1，所以有

akm=a1+tn=aatn=a

即斷言2的結(jié)論(2)成立.

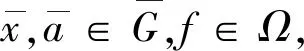
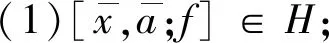
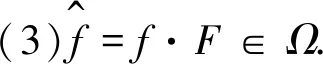
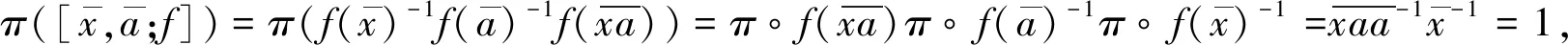
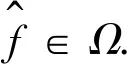
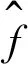
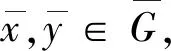
(1)

(2)

(3)

將(3)式代入(1)式得到

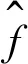
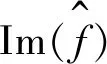
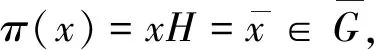
下證共軛性.因為H是G的交換正規(guī)子群，U是G的子群且滿足H≤U，所以H是U的交換正規(guī)子群；又已知K1，K2是H在G中的兩個補群，且滿足K1∩U=K2∩U，則根據(jù)Dedekind恒等式得到K1∩U=K2∩U是H在U中的補，所以要證明任意兩個補群共軛.只要證明任意兩個反同態(tài)映射的像集共軛即可.

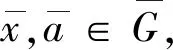
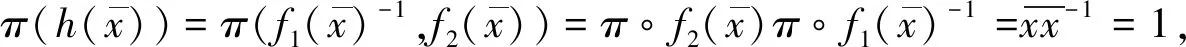
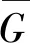
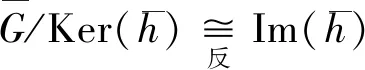
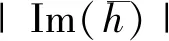
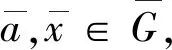
于是

即得