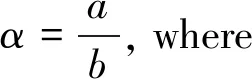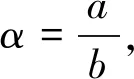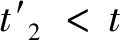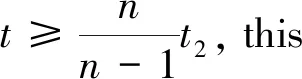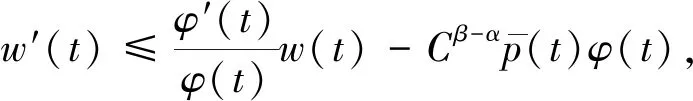Oscillation Analysis of Second Order Generalized Neutral Delay Differential Equations

WU Xiu-li

School of Mathematics and Statistics, Guangdong University of Finance and Economics, Guangzhou 510320, Guangdong, China

Abstract： In this paper, we discuss second order generalized neutral delay differential equation, by using the generalized Riccati transformation and the mean value theorem,some new oscillation criteria are obtained,which have extended the results in the cited literature.

Key words： neutral delay differential equation; Riccati transformation; oscillation criteria

0 Introduction

In this paper, the generalized neutral delay differential equation

(r(t)|z′(t)|α-1z′(t))′+q(t)f(t,x(σ(t)))=0

(1)

is discussed, wherez(t)=x(t)+p(t)x(τ(t)),α> 0, and the following conditions are satisfied:

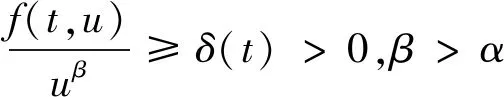
(H2)p,q∈C([t0,+∞),R+),0

(H3)r(t),τ(t),σ(t) ∈C′([t0,+∞),R+),r′(t)≥0,τ(t)≤t,σ′(t)>0,σ(t)

Recently,there have been excellent research results about the oscillatory behavior of Emden-Fowler Equation, the following examples are given.Leighton W[1]considered the equation

(r(t)x′(t))′+q(t)x(t)=0

and gave the oscillatory conditions

Grammatikopou-los M K[2]discussed the oscillations of second-order neutral delay differential equation

(x(t)+p(t)x(t-τ))″+q(t)x(t-σ)=0

and Zeng, Luo[3]studied the second-order delay differential equation

(r(t)|x′(t)|α-1x′(t))′+q(t)|x(σ(t))|β-1x(σ(t))=0

we refer to the reader to recent papers[4～13].Besides, second-order neutral delay differential equations are also used in many fields such as vibrating masses attached to an elastic bar and some variational problems[14].

In this paper,we will obtain several oscillation criteria on Eq.(1).

A solutionx(t) of Eq.(1)is said to be oscillatory if it is defined on some ray [T,+∞) withT≥0 and has unbounded set of zeros.Eq.(1)is said to be oscillatory if all solutions are oscillatory throughout[0,+∞).

In this paper,all the inequalities are satisfied fortfor sufficiently large.

First, we introduce the following lemma which is very important for the proof of our main results.

Lemma1[15]Suppose thatXandYare non-negative,then

Xd-dYd-1X+(d-1)Yd≥0d>1

where the equality holds if and only ifX=Y.

1 Main Results

Lemma2 Suppose thatx(t) is an eventually positive solution of Eq.(1).If (H1)～(H3) hold, then

z′(t)≥0z″(t)<0

(2)

(3)

wheren∈N.

Proof Suppose thatx(t) is a positive solution of Eq.(1), we assume thatx(t)>0,x(τ(t))>0 andx(σ(t))>0.then from Eq. (1),we have

z(t)≥x(t)>0

(4)

and

(r(t)|z′(t)|α-1z′(t))′=-q(t)f(t,x(σ(t)))≤0

(5)

this implies thatr(t)|z′(t)|α-1z′(t) is a decreasing function on [t,+∞), in tne following,we claim thatz′(t)≥0 fortsufficiently large.

If it is not true,then there exists at1such thatz′(t)<0 fort>t1.

(6)

Notice thatz(t)=x(t)+p(t)x(τ(t)) and the condition (H3), we get that

x(t)=z(t)-p(t)x(τ(t))≥z(t)-p(t)z(τ(t))

according to Eq.(4),we get

x(t)≥z(t)(1-p(t))

(7)

Notice that (H1) and Eq.(7), we have

0=(r(t)z′(t)α)′+q(t)f(t,x(σ(t)))≥(r(t)z′(t)α)′+q(t)δ(t)xβ(σ(t))

and

(r(t)z′(t)α)′+q(t)δ(t)(1-p(t))βzβ(σ(t))≤0

(8)

Considering the fact that (r(t)z′(t)α)′=r′(t)z′(t)α+αr(t)z′(t)α-1z″(t)≤0 andz′(t)≥0 and (H3) we claim that there existst2such thatt>t2,

z″(t)<0

(9)

and

(10)

Lemma3 Suppose thatx(t) is an eventually positive solution of Eq.(1)and(H1)～(H3) hold.Define the functionw(t) by the Riccati transformation

thenw(t)>0 and

(11)

and

(12)

Proof From Lemma 2 obviously,w(t) > 0 fort>t1, and we obtain

(13)

from Eq.(8) and (H1), we have

(14)

From (2),

(15)

combine Eq.(13)～Eq.(15),we get

In Lemma 1,we give

then,we have

this completes the proof of Eq.(12).

Lemma4 Suppose thatx(t) is an eventually positive solution of the Eq.(1)and (H1)～(H3) hold.Then,fortsufficiently large,and a positive constantC, the following inequality is satisfied

(16)

Proof From Eq.(3), we have

thus

this completes the proof of Eq.(16).

Theorem1 Assume that (H1)～(H3) hold,if there exists a function

φ(t)∈C′([t0,+∞),R+)

such that for any positive numberC

Proof Suppose that Eq.(1) has a nonoscillatory solutionx(t),Without loss of generality,we may assume thatx(t)>0, the case ofx(t)<0 can be considered by the same method.We processed as in Lemma 3 to have Eq.(1) andw(t)>0,we use the results of ODE, the following inequality holds:

(17)

Theorem2 Assume that (H1)～(H3) hold,if there exists a function

φ(t)∈C′([t0,+∞),R+)

such that for any positive numberC

Proof Suppose that Eq.(1) has a nonoscillatory solutionx(t).Without loss of generality,we may assume thatx(t)>0, the case ofx(t)<0 can be considered by the same method.We processed as in Lemma 3 to have Eq.(1) andw(t)>0，integrating Eq.(12) fromt0tot, the following inequality holds:

(18)

Theorem3 Assume that (H1)～(H3) hold.If there exists a function

φ(t)∈C′([t0,+∞),R+)

such that for any positive numberC

Proof Suppose that Eq.(1) has a nonoscillatory solutionx(t):Without loss of generality,we may assume thatx(t)>0,the case ofx(t)<0 can be considered by the same method.We processed as in Lemma 4 to have Eq.(1) andw(t)>0,integtating Eq.(16) fromt0tot, the following inequality holds:

(19)