基于空中機動目標攔截的制導和引信及戰斗部一體化設計研究

汪金奎， 婁文忠， 劉偉桐， 蘇子龍

(北京理工大學 機電學院, 北京 100081)

0 引言

制導和引信一體化(GIF)技術已經成為引信技術的重要發展方向之一[1-4]。空中機動目標攔截問題中，圖像導引頭或雷達導引頭通常作為防空導彈的感知方式，可以抵近獲得目標的高精度方位信息，但圖像導引頭或雷達導引頭通常存在近距盲區[5-6]，進入近距盲區后導引頭處于失效狀態,目標的位置無法觀測。引信與戰斗部(簡稱引戰)配合應用于此類作戰環境，對其起爆控制算法的研究主要是最佳起爆延時和最佳起爆方位角的計算；隨著防空目標機動能力的提升,進入視野盲區后目標的位置更加難以預測，基于目標方位的精確延時設計更加困難。雖然也有通過2階、3階多項式來描述彈目相對運動[7],但其采用的是目標機動可預測的先驗信息，實際情況中目標的機動特性可能完全無法預測，其在視野盲區內的位置分布具備隨機特性。目標最佳起爆方位角的傳統方法采用定向戰斗部，但定向戰斗部不僅設計復雜，而且依賴精確的彈目相對方位信息[8]。

在目標無法精確預測的情況下，本文提出制導和引信及戰斗部一體化設計方法，針對近距盲區內目標機動不確定性問題，考慮目標的有限機動能力，分析目標的可行狀態集；使用常規周向破片戰斗部作為毀傷元，研究制導終點彈目相對位置與相對速度對目標攔截能力的影響，解算進入盲區前最優彈目相對位置、相對速度與引信最佳起爆時間。

針對末端狀態約束的目標攔截方法近些年來也是研究的熱門[9-12]，其大都基于線性化系統模型。采用最優控制理論對最優控制量進行求解。本文基于Gauss偽普法[13]，設計末端多狀態約束的制導方法，使攔截導彈在彈道末端達到最優攔截狀態。最后對提出的算法進行仿真驗證。

1 彈目交會模型

防空導彈與目標交會時，在攔截平面內存在如圖1所示的交會模型。假設導引頭存在近距盲區r,以防空導彈戰斗部中心為坐標原點，進入導引頭盲區時，目標的相對位置為[xt0,yt0]，目標視線角為θt0,目標空速為vt,導彈空速為vm，則存在：

xt0=r，

(1)

yt0=rtanθt0.

(2)

圖1 彈目交會模型Fig.1 Missile-target encounter model

目標存在法向機動能力at，由于目標機動能力無法預測，可假設其最大機動能力atmax與速度的平方具有線性關系，即有

(3)

式中：kat為比例系數，在確定目標類型的情況下，kat可根據實際情況選取。

2 常規戰斗部破片飛散模型

基于全向飛散破片戰斗部建立戰斗部破片飛散模型。相對于定向戰斗部或桿式殺傷戰斗部而言，全向飛散破片戰斗部要求破片的數量多，戰斗部裝藥量大，但同時定向戰斗部或桿式殺傷戰斗部在彈道終點目標方位丟失時破片會完全脫靶，而全向飛散破片戰斗部仍具備毀傷能力。

靜態爆炸條件下，破片前、后飛散邊界飛行方向與彈軸前向夾角分別為φf、φb,則破片靜態主飛散角φ可表示為

φ=(φf+φb)/2.

(4)

動態條件下，破片分散方向角與導彈速度相關，靜爆條件下破片初速為vps，則動態前、后飛散邊界φfp、φbp與主飛散角φp可分別表示為

φfp=arctan (sinφf/(cosφf+vm/vps))，

(5)

φbp=arctan (sinφb/(cosφb+vm/vps))，

(6)

φp=arctan (sinφ/(cosφ+vm/vps)).

(7)

主飛散方向上破片動態初速度vpd0為

(8)

取破片的飛行阻力系數c，根據牛頓阻力定律，其運動微分方程[14]為

(9)

式中：mp為破片質量；vpd為破片飛行速度；ρ為當地空氣密度；S為破片阻力面積。破片速度時間衰減關系為

(10)

3 引戰配合模型

迎擊攔截是一種典型的攔截模式，可以實現破片與目標之間較大的相對速度，增大破片的毀傷能力。設防空導彈在位置xm1處引爆戰斗部，如圖2所示，由于導彈進入視野盲區時間極短，防空導彈空速可設為常量，以目標進入盲區的時刻為計時零點，引信延期時間為t1，因此有

xm1=vmt1.

(11)

圖2 盲區內破片與目標交會狀態Fig.2 Intersection of fragment and target in blind zone

起爆點處彈目視線角為θt1,首先假設目標進入視野盲區后無機動，則

tanθt1=yt1/(xt0-xm1).

(12)

(1)式、(2)式、(11)式代入(12)式，可得

(13)

在目標無機動假設下，定義破片飛散速度為vp、破片飛行時間為t2，則在攔截點處有

(14)

(15)

式中：vpd為主飛散方向上破片動態速度。

由(14)式、(15)式可得

(16)

實際情況下，目標在導引頭視野盲區內存在機動能力。當目標以最大機動能力躲避導彈攔截時，目標偏離攔截視線的距離最遠，此時目標偏離攔截視線的距離為

m=0.5atmax(t1+t2)2，

(17)

即目標的可行區域近似分布在以m為半長軸的橢圓區域內。為實現目標的可靠攔截，令防空導彈破片完全覆蓋目標的可行區域，即破片前、后飛散邊界與橢圓相切。為方便計算，可以認為破片前、后飛散邊界與目標可行區域相切于橢圓長軸處，如圖2所示，因此

(18)

最佳攔截方案的彈目速度矢量夾角為破片動態主飛散角，由(7)式可得

θt1=arctan (sinφ/(cosφ+vm/vps)).

(19)

由(14)式、(15)式、(18)式可得

(20)

(21)

(22)

對(22)式求解并取小值，可得

(23)

(23)式代入(20)式可求得引信起爆時間t1,代入(16)式可求得進入盲區時最佳的彈目視線角θt0.

4 終端視線角與彈目速度夾角約束制導律

根據目標進入視野盲區的視線角約束θt0和彈目速度矢量夾角θt1的約束，末端彈目距離為r/cosθt0.

由于無法獲取目標準確的機動信息，因此可將目標的機動看作系統擾動，如圖3所示，定義狀態向量x=[R,θv,θmt]，其中R為彈目視線距離，θv彈目速度矢量夾角，θmt為視線角與速度夾角，建立彈目相對運動方程如下：

(24)

(25)

(26)

式中：am為導彈的法向過載。

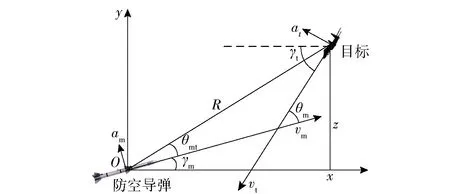
圖3 目標攔截幾何Fig.3 Target intercept geometry

定義xf為末端狀態約束，即

xf=[r/cosθt0,θt1,θt0].

(27)

考慮到法向機動能力有限，因此還存在導彈最大機動能力約束：

a≤amax.

(28)

針對本文多約束末制導問題，其非線性特性使得難以求出精確的解析解，本文采用Guass偽譜法對非線性彈目運動方程進行在線軌跡優化。Guass偽譜法是求解多約束控制問題最優解的一種數值方法，應用Largrange插值多項式對離散的系統狀態變量機控制變量進行擬合逼近,以此將原系統微分方程、約束方程等轉化為代數方程[15]，進而數值逼近求解。考慮到終端狀態誤差最小和最少的能量消耗，同時為了增加尋優算法的收斂區域，增強制導算法的魯棒性，把末端狀態的約束加入性能指標中，選擇二次型性能指標函數為

(29)

式中：tf為優化過程中的導彈飛行時間。

5 仿真實驗與結果分析

5.1 視距盲區內最優攔截仿真驗證

為驗證近距盲區內引戰配合設計，假設破片在動態飛散角內均勻飛散，為符合實際情況，可假定在二維平面內分布的破片數量N為50個，導引頭近距盲區為200 m，破片初始速度為1 600 m/s，破片采用球形預制破片，其余相關參數如表1所示。

表1 引戰配合仿真參數Tab.1 Simulation parameters

定義當破片和目標的相對距離小于3 m時，表示破片成功擊中目標。由于當前空中目標的機動能力通常小于100g[14]，目標機動能力系數kat可假定為0.01，在目標速度300 m/s下可產生91.8g的可用過載，重力加速度為9.8 m/s2. 由于本文提出的引戰配合設計方法在目標無法達到最大機動能力時仍能可靠攔截，目標在盲區機動時，可在機動能力范圍內隨機選擇法向加速度大小。設定不同的目標速度、目標實際機動能力，通過(16)式、(19)式、(23)式計算可得最優彈目交會視線角、速度矢量夾角以及引信最佳起爆時間，如表2所示。

根據算例參數，通過設定不同的目標實際過載，對典型目標攔截，如軍用運輸機攔截條件下，破片與目標交會情況進行可視化仿真驗證。目標速度300 m/s的彈目交會情況下仿真結果如圖4所示。由圖4可以看出，在目標極限機動能力條件下，破片飛散后沿處實現對目標的攔截。實際應用中，計算最優引戰配合參數時可將破片飛散角適當縮小，或將目標機動能力增大，以保證在極限條件下對目標的攔截能力。圖4同時表明，在多種因素同時影響下，可以通過調整戰斗部的設計，如改變破片飛散角、破片速度來實現所需的攔截方案。

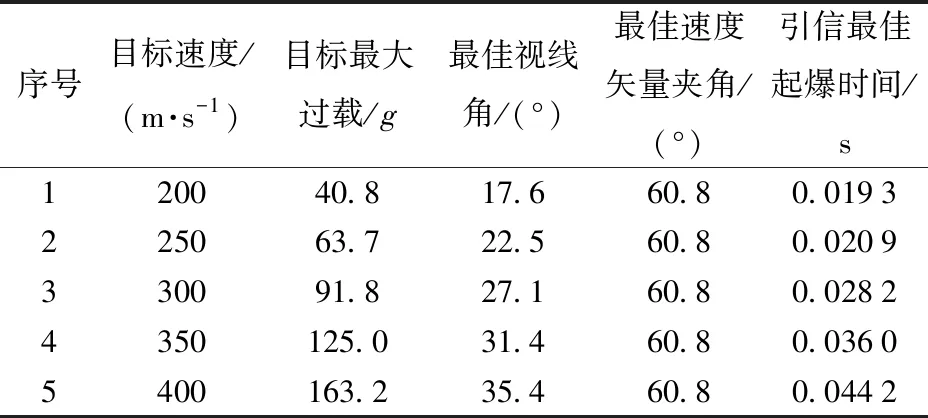
表2 最佳引戰配合參數算例Tab.2 Simulated results of example

圖4 典型工況下對機動目標攔截情況Fig.4 Interception of maneuvering targets under typical conditions

本文提出算法對目標的攔截能力受目標飛行速度、目標機動能力、導引頭視野盲區大小的影響，理論上可以計算任何目標速度下的戰斗部最佳起爆時間。但受破片有效毀傷半徑和破片密集程度影響，本文只給出了300 m/s的算例，當前可以適用于預警機、軍用運輸機等亞音速飛行器的攔截。隨著導引技術和戰斗部技術的提高，該方法的適用性將更廣。

5.2 終端多約束制導律仿真

目標類型、速度以及機動能力通常可由地面探測設備獲取，以攔截目標最大速度300 m/s，最大可用過載91.8g工況為研究算例，為實現彈目終端位置、視線角與速度矢量夾角同時約束，設定：

(30)

假設導彈的機動能力范圍為70g，即

-70g

(31)

根據末端狀態約束條件，使用Gauss偽譜法求解目標在不同方向上運動時導彈對目標的攔截情況，攔截初始狀態如表3所示。

表3 彈目初始狀態Tab.3 Initial states of missile and target

圖5(a)為彈目交會彈道，其中γt為目標的速度方向角，在目標不同的運動方向上，導彈均能實現對目標的攔截。圖5(b)、圖5(c)分別為彈目速度夾角與視線速度夾角，其在不同初始狀態下均能收斂到引戰配合所需的終端約束條件。

圖5 多約束下狀態量收斂情況Fig.5 Convergence of state under multiple constraints

圖6為導彈法向需用過載。由圖6可以看出：導彈的控制量在彈道前期，并且不同目標狀態下，導彈控制量均在約束范圍內；導彈彈道的調節主要在彈道前期，有利于彈道的穩定控制。

圖6 導彈法向需用過載Fig.6 Required acceleration in normal of missile

6 結論

針對空中機動目標攔截、導引頭存在近距盲區的問題，本文提出了一種考慮目標最大機動能力的制導和引信及戰斗部一體化設計方法，在目標進入盲區后進行任意能力范圍內的機動情況下，實現目標的可靠攔截，基于破片與目標交會模型，推導了引信最佳起爆時間、進入盲區時的視線角、速度矢量夾角的解析解；以末端彈目相對位置、視線角、速度矢量夾角為約束條件，建立彈目相對運動方程，基于Gauss偽譜法對多約束下的制導律進行數值求解。仿真分析表明，提出的引戰配合方法實現了目標任意可行范圍內的可靠攔截，基于Gauss偽譜法的在線求解多末端約束條件的制導方程，成功實現了導彈進入盲區時的狀態約束。本文提出的方法將可解決防空導彈導引頭盲區內攔截問題，提高防空導彈對機動目標的攔截能力，但該方法同時存在一定的適用性，當飛行器速度更高、機動能力更大時，對戰斗部毀傷半徑和破片密度都產生了較大的考驗；并且，當飛行器在多個方向上存在較大機動能力時，需要考慮三維情況的引戰配合，這些問題將在未來進一步研究。