粗粒土在三向卸載時的強度特性試驗研究

施維成，朱俊高，胡錫鵬，代國忠，李雄威，李書進

(1.常州工學院 土木建筑工程學院，江蘇 常州 213032；2.河海大學 巖土力學與堤壩工程教育部重點實驗室， 南京 210098；3.中交第三公路工程局有限公司，北京 101300)

強度特性是土的重要力學性質(zhì)，很多學者通過剪切或三軸加載試驗對其進行研究。卜建清等[1]通過三軸試驗研究了凍融次數(shù)、細粒含量以及圍壓對粗粒土強度特性的影響。Asghari等[2]對膠結(jié)砂進行了一系列三軸試驗，研究其強度特性。彭凱等[3]通過大型單剪儀研究了不同泥皮成分對粗粒土-混凝土接觸面強度的影響。Wang等[4]對粗粒鹽堿土進行了凍融循環(huán)下的直剪試驗，提出了兼有含鹽量和凍融循環(huán)的經(jīng)驗公式。黃茂松等[5]總結(jié)了飽和黏土、砂土及粗粒土的本構(gòu)強度理論研究現(xiàn)狀及發(fā)展趨勢。Aouali等[6]通過直剪試驗研究了纖維加固泥砂中纖維含量對強度的影響。徐肖峰等[7]使用大型直剪儀對不同剪切速率下粗粒土的強度特性進行了試驗研究。Chen等[8]對加入4種不同比例碎石的泥砂進行了三軸試驗，分析了粗顆粒和細顆粒對強度和變形的影響。Zaimoglu等[9]通過一系列無側(cè)限抗壓試驗、直剪試驗研究了隨機分布的聚丙烯纖維對細粒土強度特性的影響。Aslani等[10]通過大型直剪試驗對石柱加固粘土的剪切強度進行了研究。Deganutti等[11]對顆粒材料的摩擦角進行了研究，認為摩擦角取決于顆粒的大小和形狀。

卸載是工程中常見的工況，比如水庫泄水、基坑開挖等等，然而，對卸載條件下土的強度研究則相對較少，部分學者對細粒土的卸載強度進行了研究。蔡建等[12]從理論上推導了土的卸載抗剪強度指標計算方法，張玉等[13]使用真三軸儀對黃土進行了平面應變條件下的側(cè)向卸載試驗，何世秀等[14]通過對粉質(zhì)黏土的卸載剪切試驗整理分析，認為這種土近似符合Matsuoka-Nakai準則，王大雁等[15]研究了經(jīng)K0固結(jié)后蘭州凍結(jié)黃土在徑向卸載狀態(tài)下的應力-應變行為，認為可用主應力差漸近值與破壞比之間的關(guān)系來估算破壞強度。李加貴等[16]對黃土進行了圍壓減小、軸壓不變的三軸側(cè)向卸荷剪切試驗，得到的強度參數(shù)低于三軸壓縮試驗結(jié)果。

粗粒土在土石壩等工程中應用廣泛，且經(jīng)歷包括加載、卸載在內(nèi)的復雜工況。目前，對粗粒土強度特性的研究一般還是基于粗粒土的加載試驗，在卸載尤其是不同中主應力系數(shù)情況下，三向卸載條件下的粗粒土強度特性試驗研究基本未見報道，筆者使用真三軸儀對粗粒土進行等q、等b三向卸載試驗，研究粗粒土在三向卸載時的強度特性。

1 試驗儀器

試驗使用的真三軸儀可單獨控制3個方向的主應力σ1、σ2、σ3，如圖1(a)所示。豎向采用剛性板加壓，水平向分別采用水囊和復合加壓塊加壓，如圖1(b)所示。

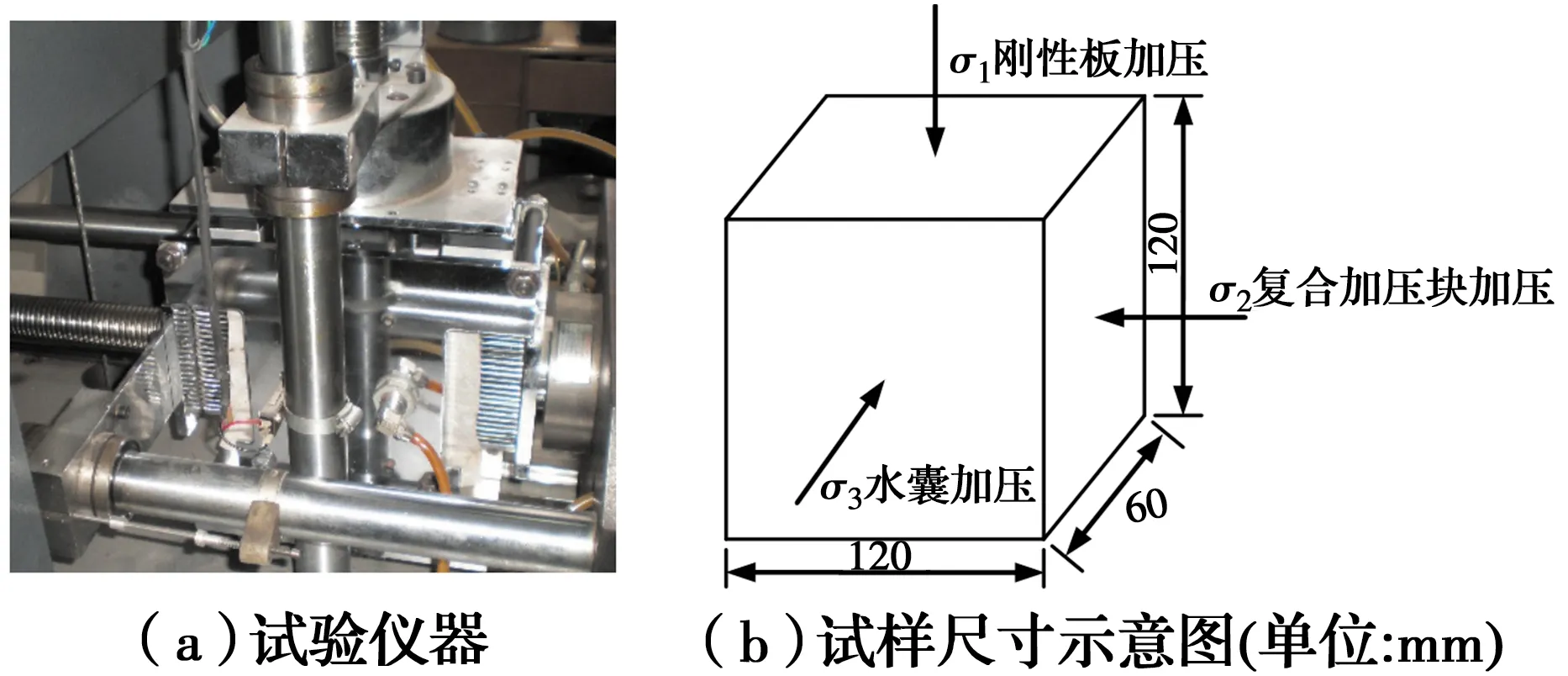
圖1 試驗儀器及試樣尺寸示意圖Fig.1 Test instrument and the sketch map of sample dimension

2 試驗材料、試驗方法及應力路徑

2.1 試驗材料

試驗土料為雙江口心墻堆石壩的粗粒土，占總重量70%的顆粒粒徑介于5～10 mm之間，30%的顆粒粒徑小于5 mm，最小干密度1.54 g/cm3，最大干密度1.96 g/cm3。土樣分5層擊實，控制干密度ρd=1.91 g/cm3，相對密度0.90，為簡單起見，制樣和試驗時的試樣都為干樣。試樣尺寸為120 mm×60 mm×120 mm的長方體。

2.2 試驗方法

2.3 應力路徑

等q、等b試驗時，保持q和b為常數(shù)，p為變量，算出相應的3個方向主應力σ1、σ2、σ3，卸載時，3個方向主應力都以0.2 kPa/s的速度減小，圖2為不同b值時實測的σ1、σ2、σ3隨時間t的變化曲線。可以看出，等q、等b試驗中，3個方向的主應力σ1、σ2、σ3都在不斷等量減小，為三向等量卸載試驗。

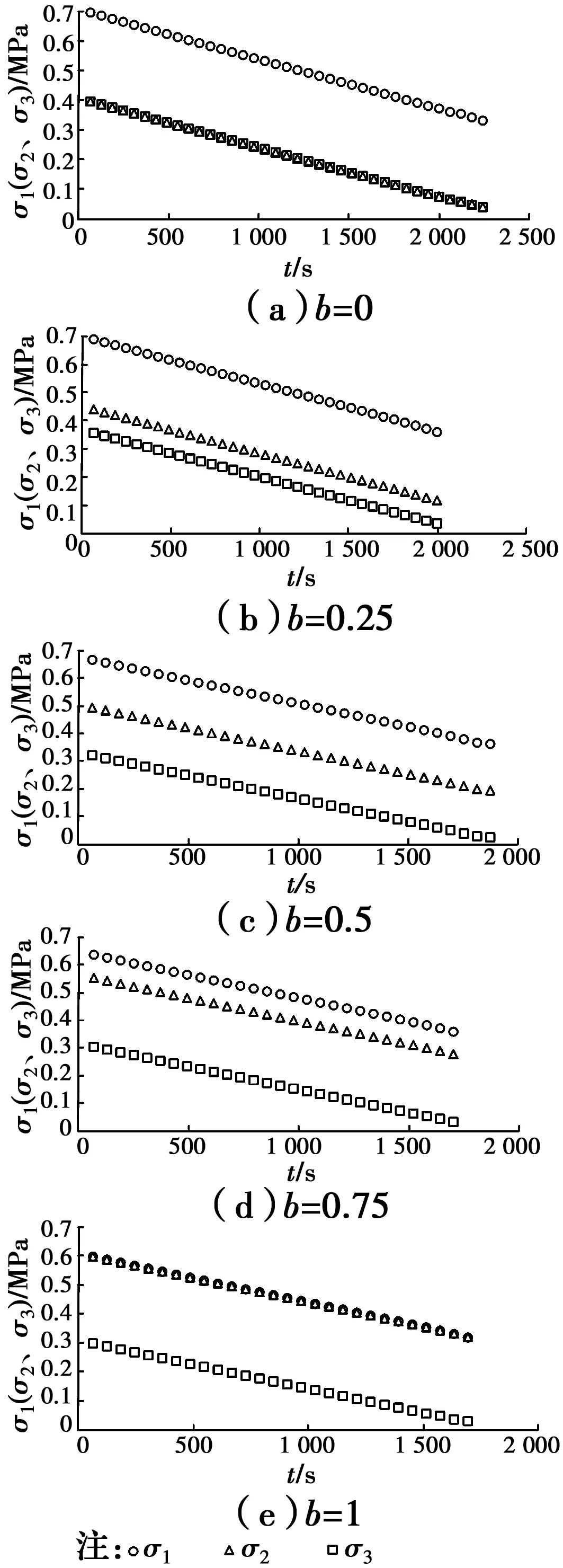
圖2 應力時程曲線Fig.2 The stress time history curves

3 試驗結(jié)果分析

表1和表2分別列出了等q、等b試驗初始狀態(tài)和破壞狀態(tài)3個方向的主應力大小，表2還算出了內(nèi)摩擦角φb(φb=arcsin[(σ1-σ3)/(σ1+σ3)])和破壞應力比Mb(=q/p)。比較表1和表2可以看出，破壞狀態(tài)的3個方向主應力都比初始狀態(tài)要小，為三向卸載。由表2可見，在三向等量卸載條件下，粗粒土的強度參數(shù)與中主應力系數(shù)b有關(guān)；對于不同的b值，b=0時的內(nèi)摩擦角φb最小，破壞應力比Mb最大；隨著b的增加，內(nèi)摩擦角φb逐漸變大，b=0.5時內(nèi)摩擦角φb達到最大，當b值繼續(xù)增大時，內(nèi)摩擦角φb則隨著b的增大而減小，b=1時的內(nèi)摩擦角比b=0時的大；破壞應力比Mb隨著b的增大而減小，且隨著b的增大，減小的梯度在逐漸減小。

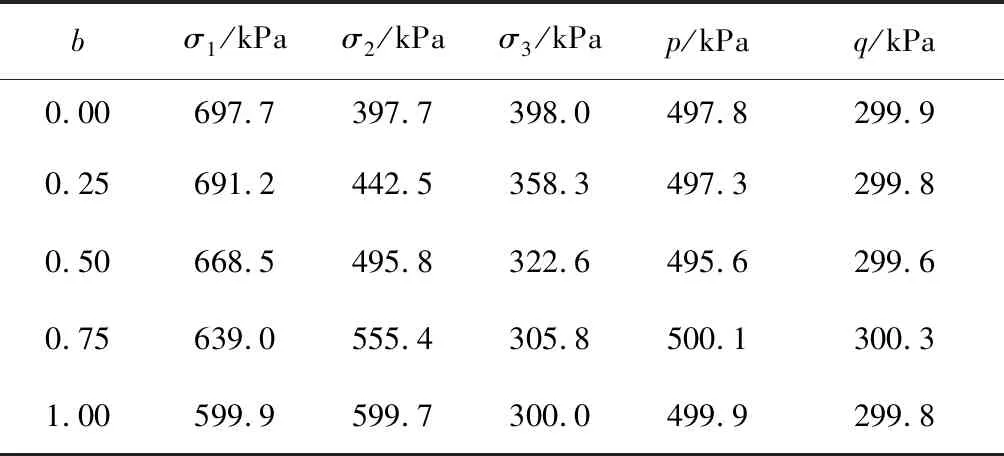
表1 等q、等b試驗初始狀態(tài)3個方向主應力大小匯總表Table 1 Summary table of principal stresses in three directions in the initial state obtained from the q- and b- constant tests

在三向主應力σ1、σ2、σ3(σ1≥σ2≥σ3)共同作用下，剪切強度參數(shù)可以認為受3個因素共同影響：因素1，在σ2側(cè)向約束下σ1、σ3間的剪切作用σ1-σ3；因素2，在σ1側(cè)向約束下σ2、σ3間的剪切作用σ2-σ3；因素3，在σ3側(cè)向約束下σ1、σ2間的剪切作用σ1-σ2。內(nèi)摩擦角φb在b值較小時隨著b的增大而增大，在b值較大時隨著b的增大而減小的規(guī)律可以由這3個因素的共同影響來解釋。

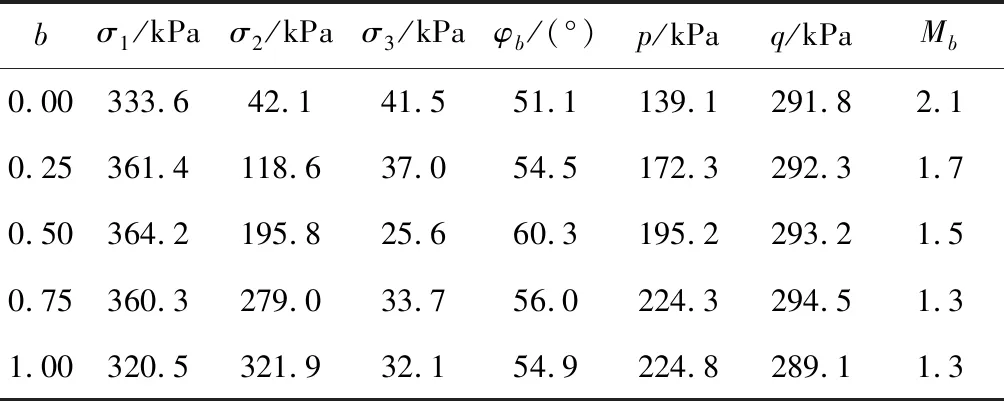
表2 等q、等b試驗破壞狀態(tài)3個方向主應力大小匯總表Table 2 Summary table of principal stresses in three directions in the failure state obtained from the the q- and b- constant tests

當b=0時，σ2=σ3，σ2-σ3=0，即在σ1側(cè)向約束下，σ2、σ3間的剪切作用為0，“因素2”不會對試樣的剪切破壞產(chǎn)生影響，也就是不會對剪切強度參數(shù)產(chǎn)生影響；σ1-σ2=σ1-σ3，“因素1”和“因素3”都是在σ3側(cè)向約束下的剪切作用σ1-σ3。

當b從0開始增大，但仍處于較小值時(如試驗中b=0.25時)，隨著b的增大，σ2-σ3增大，在σ1側(cè)向約束下，σ2、σ3間的剪切作用增大，有助于試樣剪切破壞，所以，“因素2”使剪切強度參數(shù)減小，但由于σ2-σ3數(shù)值較小，這個影響也較小；隨著b的增大，σ1-σ2減小，即在σ3側(cè)向約束下，σ1、σ2間的剪切作用減小，“因素3”使剪切強度參數(shù)增大；隨著b的增大，σ2增大，“因素1”的σ2側(cè)向約束增大，使剪切強度參數(shù)增大。綜合3種因素來看，在b值較小時，剪切強度參數(shù)隨著b的增大而增大。

當b繼續(xù)增大，σ2-σ3繼續(xù)增大，“因素2”使剪切強度參數(shù)減小的影響也繼續(xù)增大；而σ1-σ2繼續(xù)減小，在σ3側(cè)向約束下，σ1、σ2間的剪切作用繼續(xù)減小，“因素3”繼續(xù)使剪切強度參數(shù)增大；“因素1”中的σ2側(cè)向約束繼續(xù)增大，也是使剪切強度參數(shù)增大的因素。當b增大到某一值時(如試驗中b=0.5時)，“因素2”使剪切強度參數(shù)減小的影響與“因素3”、“因素1”使剪切強度參數(shù)增大的影響相同時，內(nèi)摩擦角達到最大值。

當b增大到較大值時(如試驗中b=0.75時)，σ2-σ3增大到較大值，而σ1-σ2則減小到較小值，此時“因素2”使剪切強度參數(shù)減小的影響超過“因素3”、“因素1”使剪切強度參數(shù)增大的影響，內(nèi)摩擦角較b=0.5時開始減小。

當b=1時，σ1=σ2，σ1-σ2=0，σ2-σ3=σ1-σ3，“因素3”不會對剪切強度參數(shù)產(chǎn)生影響；“因素1”和“因素2”都是在σ1側(cè)向約束下的剪切作用σ1-σ3。和b=0時相比，σ1的側(cè)向約束要強于σ3的側(cè)向約束，故b=1時的剪切強度參數(shù)比b=0時的大。

4 強度準則適用性研究

筆者曾根據(jù)粗粒土的三向加載試驗得到粗粒土應力不變量強度準則和角隅函數(shù)強度準則，將這些強度準則與等q、等b試驗得到的試驗結(jié)果進行比較，以驗證其對粗粒土三向卸載情況的適用性。

4.1 應力不變量強度準則

筆者曾提出應力不變量表示的粗粒土強度準則[17]，如式(1)所示。

(1)

式中：I1、I2、I3分別為第一、第二、第三應力不變量，kf為常量，與材料性質(zhì)有關(guān)。

對于粗粒土，假設凝聚力c=0，有[17]

(2)

式中：φ0為b=0時的內(nèi)摩擦角。

Lade和Duncan根據(jù)蒙特里砂試驗結(jié)果，提出Lade-Duncan強度準則[18]，表達式為

(3)

式中

(4)

Matsuoka-Nakai強度準則[19]表達式為

(5)

式中

(6)

將上述3個強度準則表示成φb與b的形式，并將π平面上的形狀畫出，與粗粒土三向卸載的試驗結(jié)果進行比較，如圖3所示。粗粒土三向卸載試驗結(jié)果顯示，b值較小時，內(nèi)摩擦角φb隨著b的增大而增大；b值較大時，內(nèi)摩擦角φb隨著b的增大而減小。顯然，3個強度準則都能反映這一規(guī)律，Matsuoka-Nakai強度準則在b值較小時與試驗結(jié)果較為接近，粗粒土應力不變量強度準則在b值較大時與試驗結(jié)果較為接近。

圖3 應力不變量強度準則與等q、等b試驗結(jié)果比較圖Fig.3 Comparison of the strength criterion of stress invariants and the q- and b- constant test results

4.2 角隅函數(shù)強度準則

土的三維強度準則通常可用角隅函數(shù)表示為

(7)

式中：Mc為b=0時的破壞應力比。

筆者曾根據(jù)粗粒土的加載試驗結(jié)果得到一個粗粒土角隅函數(shù)強度準則[20]

(8)

式中：k是與土的性質(zhì)有關(guān)的參數(shù)，可表示為[21-22]

k=1.462sinφ0-0.523 2

(9)

圖4為粗粒土角隅函數(shù)強度準則和等q、等b試驗結(jié)果，由圖4可以看出，粗粒土角隅函數(shù)強度準則與等q、等b試驗結(jié)果較為吻合。

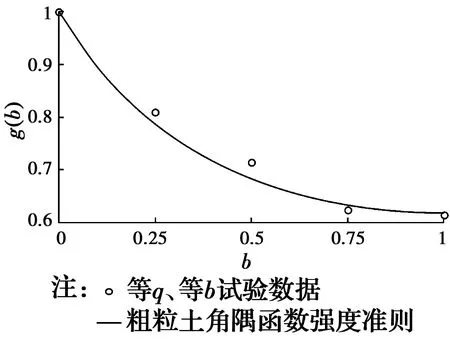
圖4 粗粒土角隅函數(shù)強度準則與等q、等b試驗結(jié)果比較圖Fig.4 Comparison of the corner function strength criterion of coarse-grained soil and the q- and b- constant test results

5 結(jié)論

使用真三軸儀對粗粒土進行了等q、等b三向等量卸載試驗，分析了三向卸載條件下粗粒土的強度特性，研究了常用強度準則對卸載條件粗粒土的適用性，得出以下結(jié)論：

1)不同b的粗粒土等q、等b三向等量卸載條件下，粗粒土的強度參數(shù)與中主應力系數(shù)b有關(guān)；b=0時的內(nèi)摩擦角φb最小，破壞應力比Mb最大；破壞應力比Mb隨著b的增大而減小，且隨著b的增大，減小的梯度在逐漸減小；內(nèi)摩擦角φb在b值較小時隨著b的增大而增大，在b值較大時隨著b的增大而減小。

2)三向主應力σ1、σ2、σ3共同作用下的剪切強度參數(shù)可以認為是受3個方向剪切的共同影響，進而可以解釋上述內(nèi)摩擦角φb隨b的變化規(guī)律。

3)Matsuoka-Nakai強度準則、粗粒土應力不變量強度準則和Lade-Duncan強度準則這3個強度準則都能反映內(nèi)摩擦角φb隨b的變化規(guī)律，Matsuoka-Nakai強度準則在b值較小時與試驗結(jié)果較為接近，粗粒土應力不變量強度準則在b值較大時與試驗結(jié)果較為接近。

4)粗粒土角隅函數(shù)強度準則與等q、等b試驗結(jié)果較為吻合。

致謝:

感謝江蘇省高校“青藍工程”、江蘇省高校優(yōu)秀中青年教師和校長境外研修計劃項目資助。