TBM空間管道動態特性分析

孫文倩，張懷亮，瞿維，熊宇

(1.中南大學高性能復雜制造國家重點實驗室，湖南長沙，410083；2.中南大學機電工程學院，湖南長沙，410083)

液壓系統是TBM(硬巖掘進機)重要的能量傳遞和控制系統，其工作性能是決定TBM 掘進效率和安全的重要指標[1]。空間管道是液壓系統的主要元件之一，在強振動環境下，一方面，外界基礎振動傳遞給管道能量，導致管道位移變形量增大，管壁產生的應力劇增，從而使管道出現疲勞破壞；另一方面，由于流固耦合作用，由管道傳遞到流體的能量造成管內流體和壓力發生較大波動，因此，有必要對基礎振動下空間管道的動態特性進行分析。PAIDOUSSIS 等[2]認為管內流體會使管道產生振動，由此輸流管道振動的相關問題逐漸引起了人們的關注。FEODOS’EV 等[3-4]建立了兩端支撐的單跨輸流管道運動的線性方程，發現當管內流速超過臨界流速時會使管道失穩。LEE等[5]推導了輸送簡諧脈動流體的三維管道系統的運動方程，提出了一種預測管道系統穩態時間響應的有效數值方法。WADHAM-GAGNON 等[6]研究了限制性和非限制性流體傳遞管道的三維非線性問題。SREEJITH 等[7]將全耦合的方程應用到核工程管道中，以流速為變量建立管道的有限元模型，研究了管道的速度響應特性。MENSHYKOVA等[8]對復合層管道的應力分布進行了研究，分析了不同結構參數下復合管道應力的變化規律。NIKOLI?等[9]分析了不同非線性模型的兩端固支輸流管道，得到了各模型的超臨界和亞臨界分叉發生的條件。KHEIRI 等[10]運用拓展的Hamilton 原理建立了一端彈簧支撐一端自由軸向流動的平動圓柱柔性管道的線性動力學方程，并分析了無振動剛體的不穩定性。JIN 等[11]運用數值求解的方法研究了輸流管道的穩定性和參數共振問題，分析了阻尼、平均流速以及質量比等物理參數對管道共振區域的影響。楊飛益[12]研究了兩端固支空間管道系統的動態響應特性，運用有限元軟件得到了空間管道最大應力隨管內流體流速和卡箍數的變化規律。黃益民等[13]通過把支撐簡化為集中質量和約束3個方向位移和旋轉的彈簧，研究了支撐剛度對輸流管系動力學特性的影響規律。付永領等[14]研究了彎管的彎曲角度對輸流管道振動特性的影響規律。俞樹榮等[15]運用有限元分析軟件進行了雙向流固耦合受力分析、單雙向流固耦合對比分析和模態分析,并考慮了脈動壓力、壁厚和管徑等參數的影響。楊超[16]研究了非恒定流下管道系統的流固耦合特性，推導了彎管的流固耦合振動方程，分析了彎管的振動力學特性。茍兵旺等[17]推導了基礎振動下兩端簡支輸流管道的數學模型，對支撐激勵下管道的動態特性進行了分析。HUANG等[18]運用伽遼金法對不同邊界條件下管道的固有頻率進行求解，并發現科里奧利力對管道固有頻率影響很小。梁峰等[19]利用多元L-P法研究了外部周期激勵下兩端固定輸流管道伴隨內共振的非線性受迫振動問題。劉森等[20]采用特征線法對基礎振動下TBM 液壓彎管管內流體的波動進行了研究，得到了基礎振動下彎管的支撐方式、振動參數、結構參數對彎管動態特性的影響規律。瞿維等[21]利用雙向流固耦合的方法建立了流體域和固體域的仿真模型，研究了不同基礎振動參數和彎管的結構參數對彎管動態特性的影響規律。綜上所述，國內外對管道振動特性的研究主要集中在管道自激振動分析上，而外激勵作用下管道動力學方面的研究較少，且主要集中于直管和彎管，對空間管道的研究較少，為此，本文作者應用有限元分析與試驗驗證相結合的方法研究強振動環境下空間管道的動態特性。

1 仿真建模

1.1 幾何建模及網格劃分

假設空間管道為均質、純彈性及各向同性的等截面圓管，管內的流體做低速運動，且不存在摩擦效應，忽略流體中的體積分離、氣穴等現象。根據TBM 現場考察資料，設定管道材料屬性與管內液壓油參數如表1所示。空間管道三維模型以及進行網格劃分后的管道模型和流體模型分別如圖1和圖2所示。

1.2 邊界條件設置

設置流固耦合接觸面(fluid solid interface)為管道內壁。管道采用兩端固支的支撐方式，通過兩端支撐傳遞給管道的激勵采用正弦位移載荷。在CFX 里面設置流體域，流體外壁設置為流固耦合接觸面，沿Y軸方向設置為流體進口(inlet)，沿X軸方向設置為流體出口(outlet)，如圖3所示。

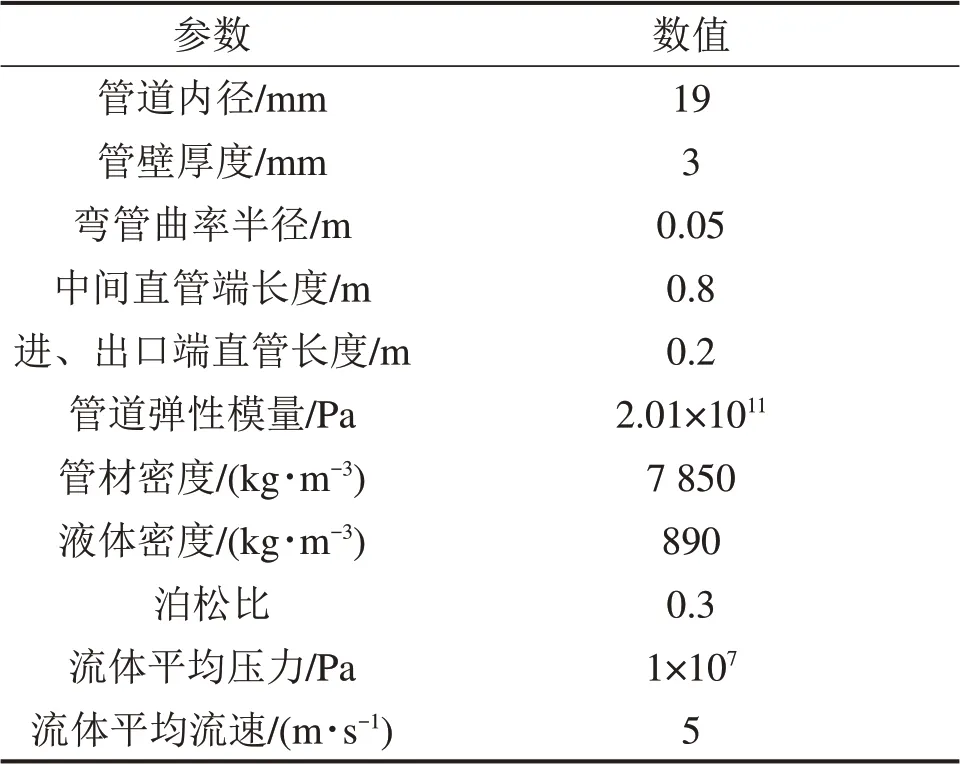
表1 管道系統相關參數Table1 Related parameters of piping system

圖1 空間管道三維模型Fig.1 3D model of space pipeline

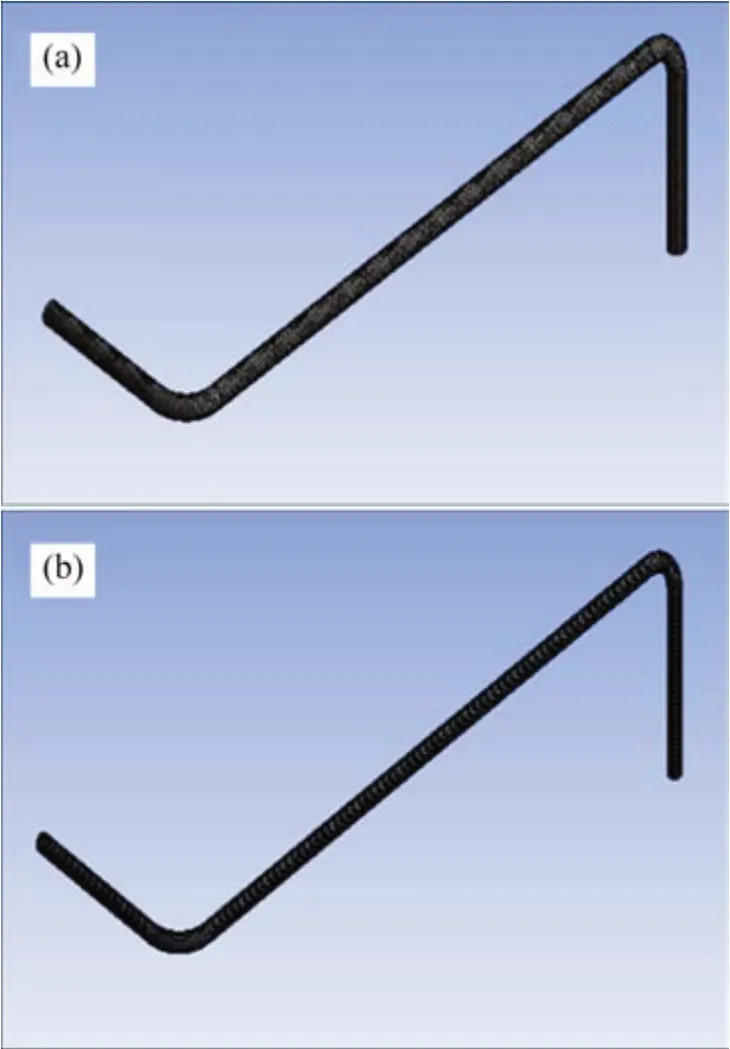
圖2 管道和流體的網格劃分Fig.2 Meshing of pipeline and fluid

圖3 流體邊界Fig.3 Fluid boundary

2 有無基礎振動時管道動態特性

仿真時設置基礎振動幅值為1 mm，頻率為60 Hz，振動方向為Y向振動，得到有無基礎振動時兩端固支空間管道應力云圖和出口壓力波動響應圖，如圖4、圖5和圖6所示。由圖4和圖5可知：有基礎振動時管道最大等效應力約為81.62 MPa，而無基礎振動時管道的最大等效應力為49.99 MPa，說明有基礎振動時管道應力會明顯增加，容易造成應力疲勞破壞。由圖6可知：有基礎振動時管道的出口壓力波動幅值顯著增加，其出口壓力波動幅值是無基礎振動時管道出口壓力波動幅值的3.98 倍。由上述研究可知：外界基礎振動對管道動態特性有很大的影響，在實際工作過程中不能忽略。

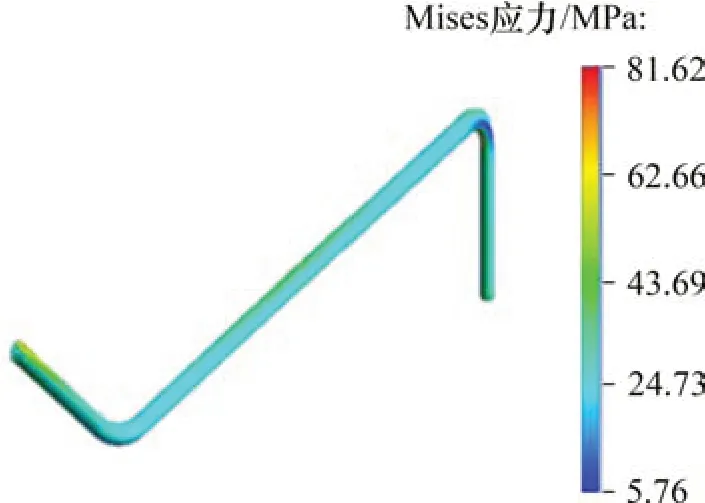
圖4 有基礎振動時管道等效應力云圖Fig.4 Equivalent stress cloud diagram of pipeline with basic vibration

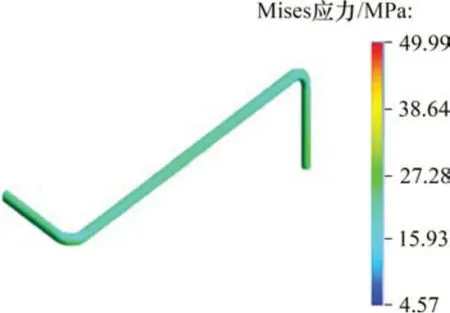
圖5 無基礎振動時管道等效應力云圖Fig.5 Equivalent stress cloud diagram of pipeline without foundation vibration

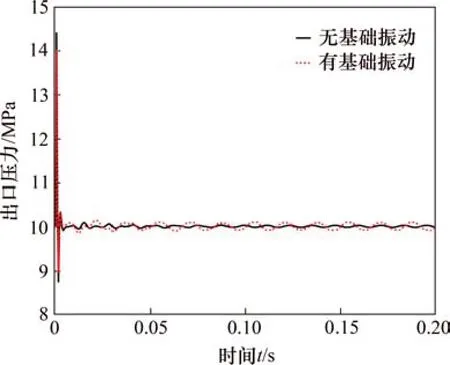
圖6 有無基礎振動管道出口壓力波動響應Fig.6 Pipeline outlet pressure fluctuation response with or without basic vibration

3 空間管道應力分析

3.1 振動參數對應力的影響

管道流固耦合仿真結束后，將仿真結果導入static structural 模塊與model 模塊進行含預應力的管道模態頻率分析，得到不同方向振動下管道一階模態頻率，如表2所示。

結合TBM 實際工作情況，設置基礎振動幅值為1 mm，基礎振動頻率f為20~200 Hz，仿真分析不同方向振動下管道最大應力隨基礎振動頻率變化的規律，結果如圖7所示。由圖7可知：當外界基礎振動頻率靠近管道模態頻率時，管道的最大應力會增加；當20≤f＜120 Hz時，X向和Y向振動在振動頻率為100 Hz 時管道最大應力最大，因為此時基礎振動頻率接近管道一階和二階模態頻率，并且X向與Y向振動作用下的管道最大應力高于Z向振動下的管道最大應力；當120＜f≤200 Hz 時，X向、Y向和Z向振動均在振動頻率為160 Hz 時，管道應力最大，因為此時基礎振動頻率接近管道三階模態頻率；Z向振動下管道的最大應力大于X向與Y向振動下管道的最大應力，前者約為后者的4.12倍，故當120≤f≤200 Hz時，應避免Z向振動。

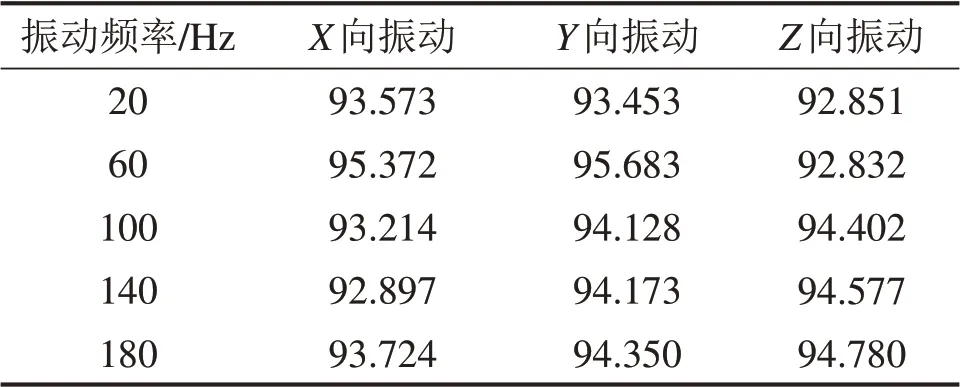
表2 不同方向振動下管道一階模態頻率Table2 First-order modal frequency of pipeline under different vibration directions Hz

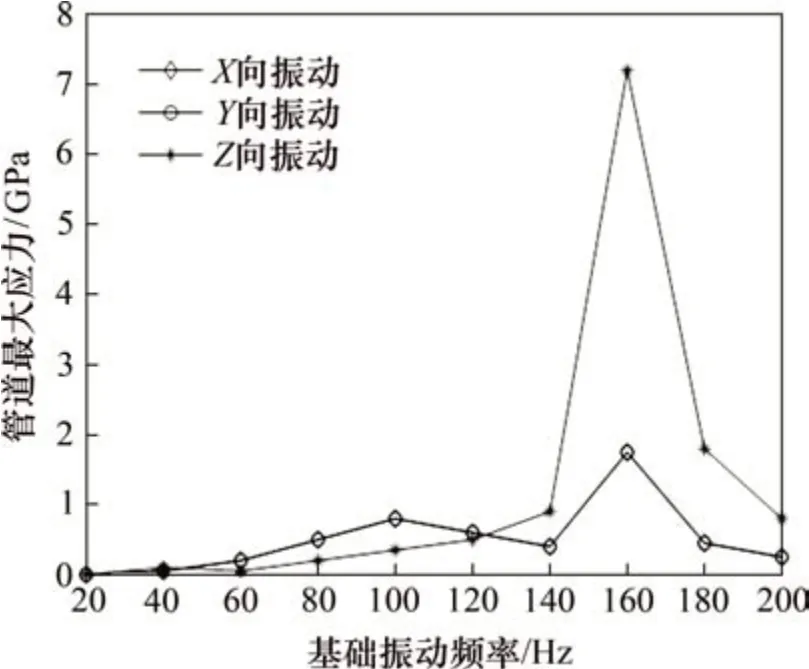
圖7 管道最大應力隨基礎振動頻率的變化Fig.7 Change of the maximum stress of pipeline with fundamental vibration frequency

設定基礎振動頻率為60 Hz，基礎振動幅值為0.5~1.5 mm，仿真得到振動方向為X向、Y向和Z向時不同基礎振動幅值下管道的最大應力，如圖8所示。由圖8可知：當基礎振動頻率一定時，管道最大應力隨著基礎振動幅值的增大而增大。這是因為基礎振動幅值越大，使得外界輸入到管道能量越多，導致管道振動加劇。與X向和Y向振動相比，Z向振動下管道最大應力增加的速率最小，即當基礎振動頻率為60 Hz 時，Z向振動對管道最大應力的影響最小。

3.2 結構參數對應力的影響

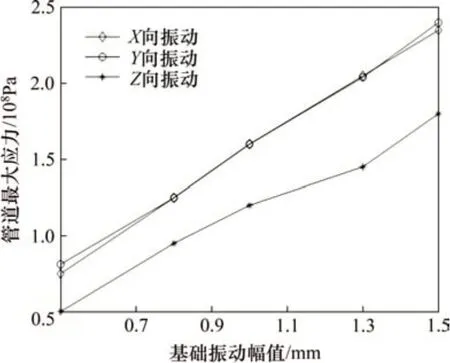
圖8 管道最大應力隨基礎振動幅值的變化Fig.8 Change of the maximum stress of pipeline with amplitude of fundamental vibration

設定基礎振動幅值為1 mm，振動頻率為60 Hz，仿真分析不同中間直管長度、管道內徑和曲率半徑對管道最大應力的影響，結果如圖9、圖10和圖11所示。由圖9可知：管道的最大應力隨中間直管長度的增大而增大。這是因為管道中間直管長度的增加導致管道模態頻率下降，管道的模態頻率接近基礎振動頻率，引起管道振動加劇。與X向和Y向振動相比，Z向振動下管道最大應力最小。由圖10可知：管道最大應力隨管道內徑的增大而減小。這是因為管道的內徑增大，使得管道的模態頻率增大，導致管道的模態頻率遠離基礎振動頻率，Z向振動下管道的最大應力小于X和Y向振動下的管道最大應力。由圖11可知：管道的最大應力隨曲率半徑的增大而增大，這是因為隨著管道曲率半徑的增加，管道的模態頻率越來越低，導致管道的一階模態頻率接近基礎振動頻率。在曲率半徑大于50 mm 后，當出口端曲率半徑增加時，對應的管道最大應力明顯大于進口端曲率半徑增加時對應的管道最大應力，說明出口端曲率半徑的變化對管道最大應力的影響比進口端的大。

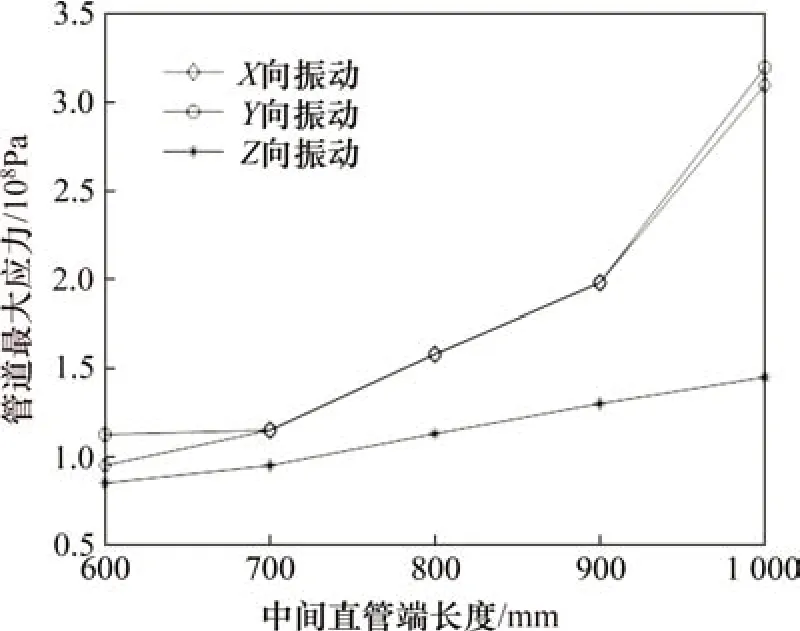
圖9 管道最大應力隨中間直管端長度的變化Fig.9 Change of the maximum stress of the pipeline with the length of the middle straight pipe end

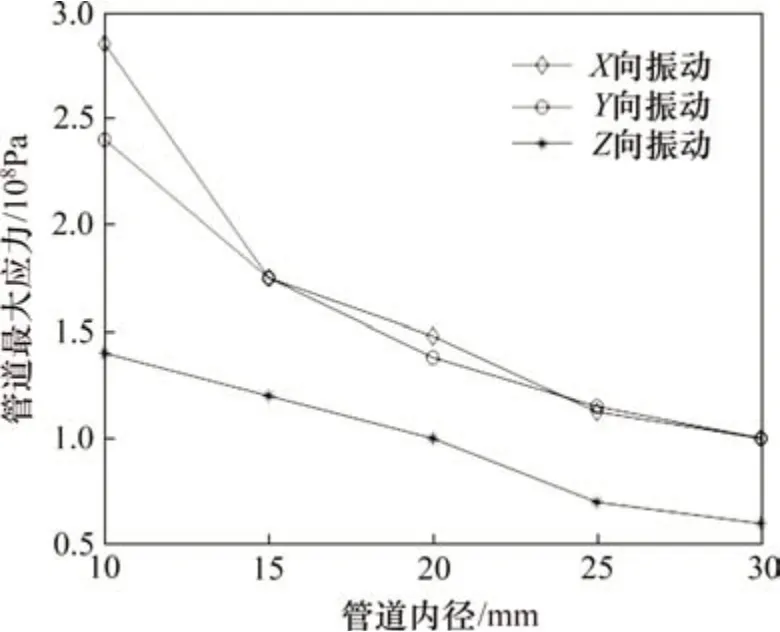
圖10 管道最大應力隨管道內徑的變化Fig.10 Change of the maximum stress of pipeline with inner diameter of pipeline

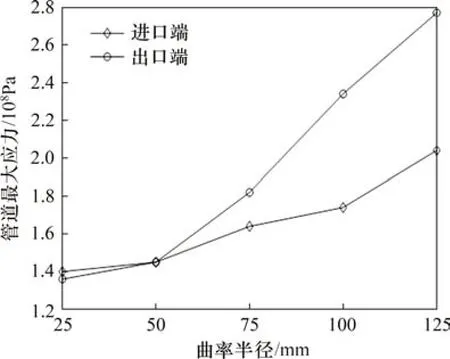
圖11 管道最大應力隨曲率半徑的變化Fig.11 Change of the maximum stress of pipeline with radius of curvature

4 空間管道出口壓力波動分析

設定振動幅值為1 mm，振動頻率變化范圍為20~200 Hz，仿真分析不同振動方向下振動頻率對管道出口壓力波動幅值的影響，如圖12所示。由圖12可知：當基礎振動頻率接近管道模態頻率時，管道出口壓力波動幅值會增大；當20≤f＜100 Hz時，X向、Y向和Z向振動同時在基礎振動頻率f為80 Hz 時達到極大值，其中Y向振動下的管道出口壓力波動幅值最大，X向振動下的管道出口壓力波動幅值最小；當100≤f≤200 Hz，基礎振動頻率為160 Hz 時，管道出口壓力波動幅值最大，這是因為此時基礎振動頻率接近管道二階模態頻率。

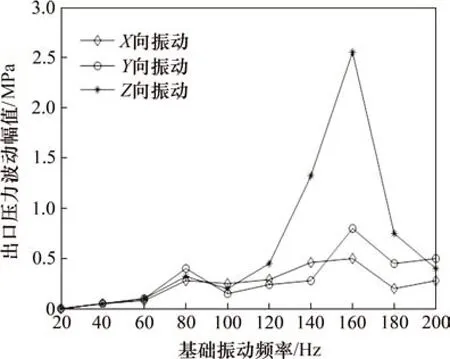
圖12 出口壓力波動幅值隨振動頻率變化的規律Fig.12 Change of outlet pressure fluctuation amplitude with vibration frequency

設定基礎振動頻率為60 Hz，分析基礎振動幅值為0.5~1.5 mm 時管道在X向、Y向和Z向振動下出口壓力波動幅值的變化，如圖13所示。由圖13可知：隨著基礎振動幅值增加，管道的出口壓力波動幅值逐漸增大。由于雙向流固耦合的作用，管道振動的加劇使得管道出口壓力波動幅值呈現增加的現象。與Y向和Z向振動相比，X向振動下管道出口壓力波動幅值最小。

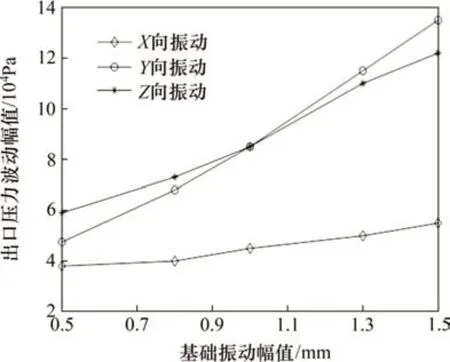
圖13 出口壓力波動幅值隨振動幅值變化的規律Fig.13 Change of outlet pressure fluctuation amplitude with vibration amplitude

5 實驗驗證

實驗系統原理如圖14所示。實驗系統由液壓控制回路系統、振動系統、實驗管道系統和數據采集系統4個部分組成。

圖14 實驗系統原理圖Fig.14 Schematic map of experimental system

設置完液壓系統參數，啟動振動臺，設置采樣頻率為1 000 kHz，得到基礎振動幅值為1.0 mm和基礎振動頻率為60 Hz時管道軸向應力的實測曲線，如圖15所示。由圖15可見：在數據采集時間為20~25 s，實驗得到管道軸向應力波峰均值為5.62 MPa，波谷均值為-5.16 MPa。對同參數條件下管道應力進行仿真，并導出同節點應力，如圖16所示。由圖16可知：仿真得到的管道軸向應力曲線與實驗得到的曲線形態大致一致，仿真得到軸向應力波峰均值約為6.44 MPa，波谷均值約為-5.54 MPa。與實驗值相比，管道軸向最大應力仿真值與最小軸向應力仿真值的相對誤差分別為14.59%與7.36%。

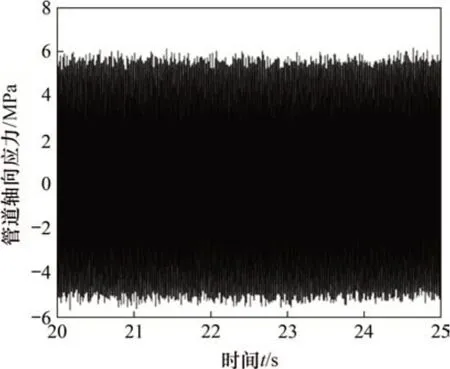
圖15 實測應力結果Fig.15 Experimental stress results

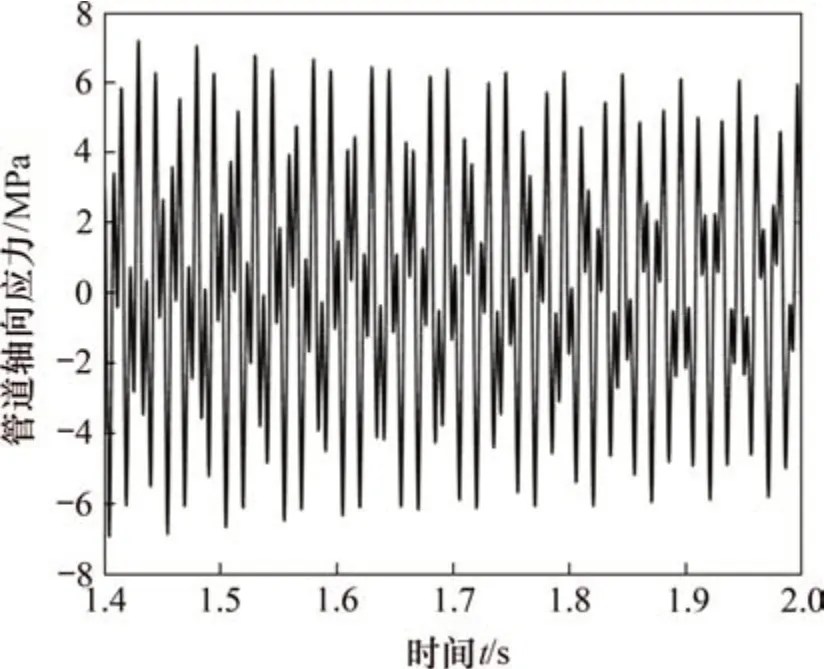
圖16 仿真應力結果Fig.16 Simulated stress results

設定基礎振動頻率為60 Hz，當基礎振動幅值從0.4 mm增加到1.2 mm時，實驗測得不同振動幅值下管道軸向應力最大值隨基礎振動幅值的變化規律，并與仿真值進行對比，如圖17所示。由圖17可知：隨著基礎振動幅值增加，管道軸向應力最大值實驗值與仿真值有相同的變化趨勢，實驗值與仿真值最大相對誤差為16.26%，平均相對誤差為12.38%，均在合理的范圍內，驗證了仿真模型的正確性。

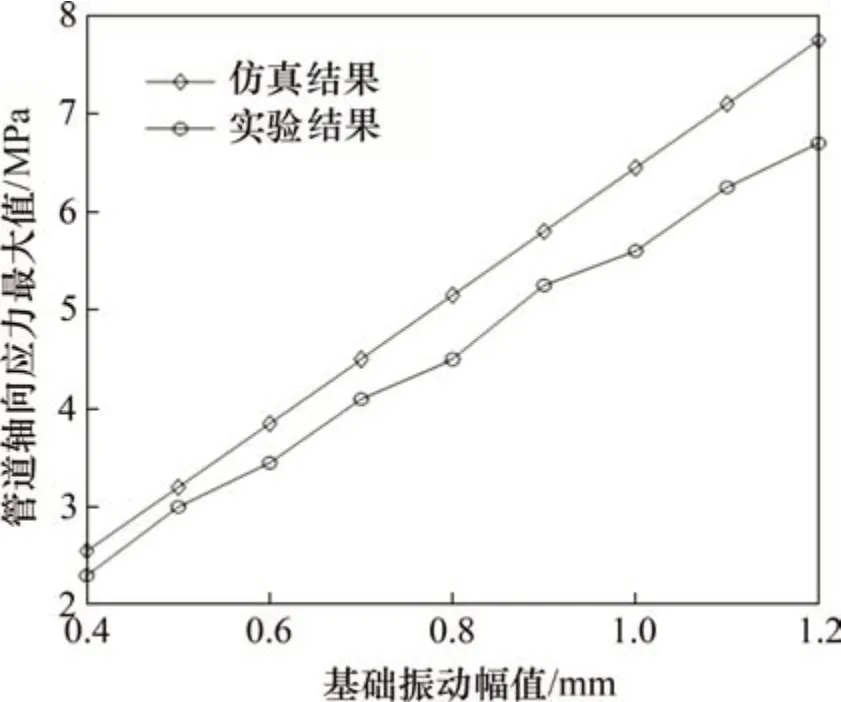
圖17 不同振幅下管道軸向應力最大值實驗結果與仿真結果對比Fig.17 Comparison of experimental and simulation results of the maxmium stress of pipeline at different vibration amplitudes

6 結論

1)建立了基礎振動下空間管道雙向流固耦合仿真模型，實驗驗證了仿真模型的正確性。

2)隨著基礎振動頻率的增大，管道的最大應力和出口壓力波動幅值均先增大后減小；當基礎振動頻率接近管道模態頻率時，管道最大應力和出口壓力波動幅值最大；隨著基礎振動幅值增大，管道最大應力和出口壓力波動幅值逐漸增大。

3)隨著管道曲率半徑的增大，管道的最大應力逐漸增大，出口端曲率半徑的變化對管道最大應力的影響比進口端的大，當出口端曲率半徑為125 mm 時，管道最大應力是進口端管道最大應力的1.35倍。