基于基因表達式編程的計算機組卷算法研究

韓 嘯，畢 波，唐錦萍

(1.東北石油大學 數學與統計學院，黑龍江 大慶 163000;2.黑龍江大學 數據科學與技術學院，黑龍江 哈爾濱 150080)

0 引 言

隨著當代教育技術及科學技術的迅速發展，傳統的教學與考試方式已漸漸無法適應現代化的教學要求，因此網絡化的教學考試已漸漸步入人們的視野。網絡化的教學考試的關鍵在于能夠快速智能地組成試卷，即在計算機上設置試題庫，并通過適當的算法挑選出試題并構成試卷，這類算法相較于傳統的人工組卷來說更為高效[1]。

通過網絡化的考試模式，不僅可以減輕教師及學校的工作量，而且更能激發學生的學習熱情、提高學生的學習效率。

目前的在線考試系統已經可以實現智能組卷、在線答題、在線閱卷等一系列功能。但由于一些現實條件的約束，各類在線考試系統在智能組卷方面還不夠成熟；大批量產生試卷時速度慢、質量差是現階段組卷算法的主要缺點。

針對現階段在線考試系統組卷速度慢、質量差、題型不均衡等不合理的問題[2]，文中首先給出了組卷問題的數學模型，將組卷問題歸結為一個約束非線性優化問題，并提出了基于基因表達式編程的自動組卷算法，將該算法用于求解組卷優化問題，實驗證明該算法有著較高的計算效率和良好的實用性。

1 常見智能組卷算法

常見的智能組卷算法包括以下4種：

(1)基于隨機算法的組卷算法。

隨機組卷算法是依據已經確定的試卷標準進行隨機抽取試題[3]，在組卷時，利用二項分布函數建立數學模型，按照試題的類型、試題的難度、知識點等約束條件進行選擇。

該算法結構簡單、易于理解，常常應用于容量較小的試題庫組卷系統中[4]。當系統中試題過多時，組卷的時間會變長且成功率低。

(2)基于回溯算法的組卷算法。

回溯算法實際上是一個類似于枚舉的搜索嘗試過程[5]，是一種選優搜索的方法，按選優條件向前搜索以達到目標,在搜索嘗試的過程中尋找問題的解，當不滿足求解條件時就進行“回溯”[6]，嘗試別的路徑，重新抽取試題。

在試題種類少、數量少的情況下，回溯算法優于隨機算法[7]。但當試題種類增多、試題量增加后，使用回溯算法生成試卷的速度明顯變慢[8]，且選取的試題不能保證是最優的，所以在智能組卷中回溯算法很少被使用。

(3)基于遺傳算法的組卷算法。

遺傳算法(genetic algorithm，GA)是一類借鑒生物界的“適者生存，優勝劣汰”的遺傳機制演化而來的隨機化搜索方法[9]。該算法采用簡單的編碼技術對試題庫中的試題進行編碼，生成初始的種群。然后通過復制、交換、突變三種操作產生下一代新的種群。并且一代一代朝向適應度函數的方向發展，直至產生滿足出卷要求的試卷。

遺傳算法在智能組卷中是比較靈活的方法，適用于具有多約束條件的組卷問題[10]。但在組卷過程中由于試題量的增加，“早熟”的問題逐漸顯現出來，所以如何提高算法執行效率，解決“早熟”問題成為了重要的研究問題。

(4)基于粒子群優化算法的組卷算法。

粒子群優化算法是模擬鳥群覓食行為而發展起來的一種基于群體協作的隨機搜索算法[11]。粒子群算法首先從試題庫中隨機抽取若干套試卷，構成最初的粒子群(每個粒子代表一套試卷)。然后，運用適應度函數計算每個粒子的值，判斷其是否符合要求。如果不符合繼續迭代，直至選取到符合要求的試卷。

粒子優化種群算法在計算大規模試題庫系統時編碼簡單，搜索速度更快，效率更高，但是不適宜處理離散的優化問題，且在選擇遺傳算子時比較麻煩。

2 組卷問題的數學模型

組卷是指從一個試題庫中在滿足給定規則的情況下，根據確定的參數及算法，從試題庫中篩選組合出一套滿足要求的、科學的、合理的試卷。

進行組卷時需要給定以下的約束條件：試題數量、總分、題型個數、題型分數等。首先用xn來表示題型，用yn來表示章節，ki=1表示選擇某題，ki=0表示不選擇某題，如表1所示。

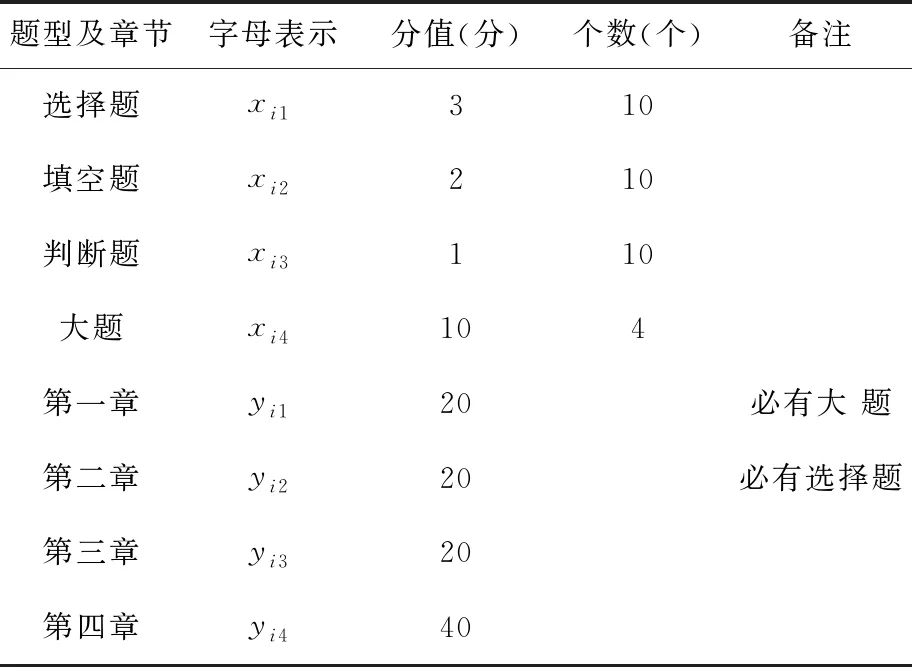
表1 試卷的約束條件

根據表1，可列出約束條件：

①試題數量約束。

(1)

②總分約束。

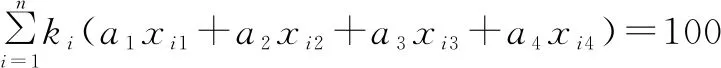
(2)

式(2)表示試卷總分為100分。

③題型個數約束。

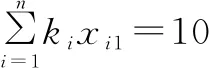
(3)

(4)

(5)

(6)

式(3)表示被選中的試題中選擇題的個數為10個，式(4)表示被選中的試題中填空題的個數為10個，式(5)表示被選中的試題中判斷題的個數為10個，式(6)表示被選中的試題中大題的個數為4個。

④每章所有題型的總分約束。

(7)

(8)

(9)

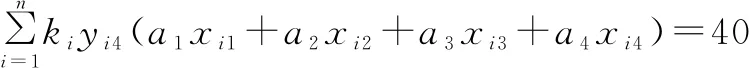
(10)

其中，yim表示第i題在第m章，

式(7)表示第一章被選中的所有試題的總分，第一章試題占20分。式(8)表示第二章被選中的所有試題的總分，第二章試題占20分。式(9)表示第三章被選中的所有試題的總分，第三章試題占20分。式(10)表示第四章被選中的所有試題的總分，第四章試題占40分。

⑤某章必有某種數量題型約束。

(11)

(12)

(13)

式(11)表示第一章被選中的題必須包含1個大題，式(12)表示第二章選中的題必須包含2個選擇題，式(13)表示第三章選中的題必須包含1個判斷題。

3 基因表達式編程算法在組卷算法中的應用

3.1 基因表達式編程算法的介紹

基因表達式編程算法(gene expression programming，GEP)是融合和遺傳算法(GA)和遺傳規劃(genetic programming，GP)的特點演化而成的算法[12]。

首先，在基因型上(句法上)，基因表達式編程算法繼承了GA的定長線性編碼的特點，以K-表達式的形式表示[13]。GEP的染色體可以由單個或多個GEP基因組成。GEP的基因是由基因的頭部h和尾部t組成，基因的頭部既可以包含函數符又可以包含終結符，而基因的尾部只能包含終結符。其中頭部的長度是根據具體的問題來決定的，基因尾部的數量由頭部數量決定，公式為：

t=h×(n-1)+1

(14)

其中，n表示所需變量數量最多的函數的參數個數(例如在常見的數學運算中，絕對值和三角函數運算n=1，而大多數的算數運算如加減乘除n=2)。GEP采用這種將頭部和尾部分開的基因形式，一方面整個基因的結構在設定了函數集合和頭部長度之后就能夠確定；另一方面，整個基因在該公式的前提下一定能夠保證結構上的正確性，而不用擔心會產生任何非法的個體。

其次，在表現型上(語義上)，GEP繼承了GP的樹形結構，稱為表達式樹。表達式樹上的葉節點表示運算數，也就是終結符。分支節點表示運算符，也就是函數符。盡管GEP采用固定長度的基因，但其對應的表達式樹形式卻千差萬別。但無論染色體怎樣變異，這些表達式樹都是有效的。GEP的基本流程框架如圖1所示[14],具體步驟如下:

①設置控制參數,選擇函數集合并設置終結符；

②創建初始種群,包含若干個代表不同解答方案的個體；

③解析GEP的基因解碼,計算每個個體的適應度值用以評價種群；

④若達到設定最大進化代數或計算精度,則進化結束,否則執行步驟⑤；

⑤根據“適者生存”原則，實施最優化保存策略；

⑥遺傳操作產生下一代：分別利用選擇、變異、倒串、插串(包括IS插串、RIS插串、基因插串)、重組(包括單點重組、兩點重組、基因重組)、隨機變量變異對群體實施遺傳操作；

⑦生成新種群，并計算各個個體的適應度函數值，然后返回步驟④。

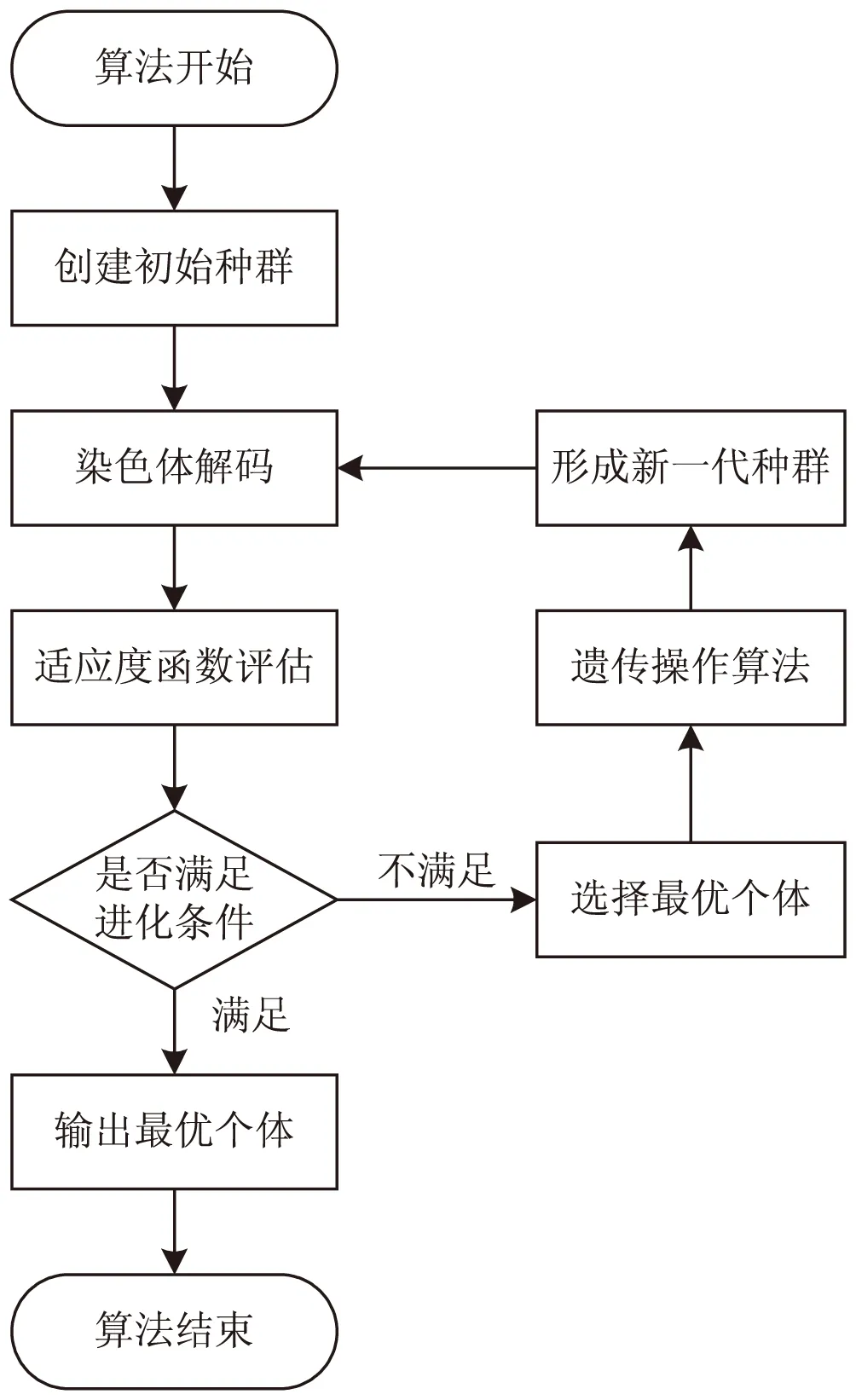
圖1 GEP算法流程

3.2 基因表達式編程的適應度函數

基因表達式編程的適應度函數是進化算法與現實問題的接口，同時也是算法演化過程的主要驅動源泉。適當的適應度函數可以評價算法所求得的問題解的優劣。適應度函數的計算一般按照以下步驟進行：

①對個體的編碼串解碼，得到個體的表現型；

②由個體的表現型計算出相應個體的目標函數值；

③依據最優化問題的類型，由目標函數值按照一定的轉換規則求出個體的適應度函數。

通過上述組卷問題的數學模型可以得到組卷問題關于基因表達式編程算法的適應度函數為：

W=1 000-(N+Q+M+P)

(15)

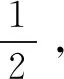
(16)

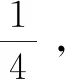
(17)

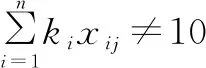
(18)

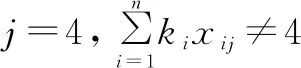
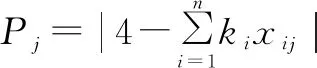
(19)

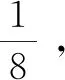
(20)

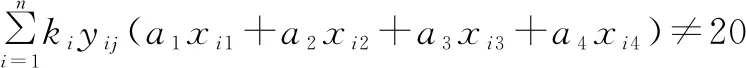
(21)

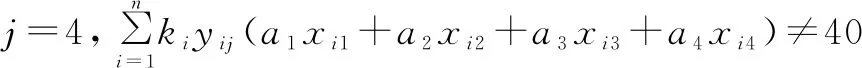
(22)

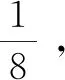
(23)

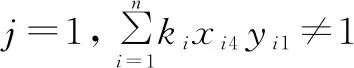
(24)

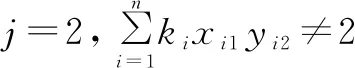
(25)

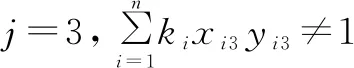
(26)

3.3 基因表達式編程的遺傳算子

GEP采用的是線性等長的編碼方式，所以基因表達式編程的遺傳操作類似于遺傳算法[15]。GEP在進行各種遺傳操作時滿足“保持基因的長度不變，尾部只能出現終結符”的原則，因此，經過遺傳操作后的子代染色體仍然是合法的。GEP區別于遺傳編程的一個特點是：GEP的一個染色體可以多次進行不同的遺傳操作，也可以不進行任何的遺傳操作。

GEP的遺傳算子包括：選擇、變異、倒串、插串(包括IS插串、RIS插串、基因插串)、重組(包括單點重組、兩點重組、基因重組)等算子[16]。對于組卷算法，只可用到變異和重組(單點重組、兩點重組)。

①變異。

在GEP中，變異是維持種群多樣性的主要方法，變異可以發生在染色體上的任何位置，染色體的變異過程如圖2所示，3-8位為尾部，變異位置用下劃線表示：

圖2 GEP染色體變異過程

②重組。

重組包括了單點重組、兩點重組和基因重組[17]。單點重組，顧名思義是在組卷染色體中尋找到兩個父代染色體，然后在兩個父代染色體中隨機選取一個交換位置，然后互相交換交換位置后面的染色體部分，從而形成兩個新的子代染色體。染色體的單點重組過程如圖3所示，3-8位為尾部，重組部分用下劃線表示。

圖3 GEP染色體單點重組過程

圖3中選擇父代1與父代2的4號基因位置為交換點，子代1是父代1交換父代2中的部分得到的，子代2是父代2交換父代1中的部分得到的。

兩點重組就是首先尋找到兩個組卷父代染色體，然后在兩個染色體上隨機選擇兩個交換位置，然后互相交換兩個位置間的部分，以達到產生兩個新的子代染色體的目的。染色體的兩點重組過程如圖4所示，3-8位為尾部，重組部分用下劃線表示。

圖4中子代1、子代2是父代1、父代2以2號位置和4號位置為重組點交換中間部分得到的。

4 仿真結果與分析

文中構造了一個題目總數為1 000道題的題庫進行實驗，其中1～300題為選擇題，301～600題為填空題，601～800題為判斷題，801～1 000題為大題。

圖4 GEP染色體兩點重組過程

實驗環境為：Windows7操作系統，CPU為i5-4210 M，內存為4 G，使用python3.7編程實現。

程序中變異、單點重組、兩點重組的概率為P=(0.28,0.41,0.31)，則實驗使用參數如表2所示。適應度函數越接近1 000則得到的結果越好，當適應度函數為1 000時，達到最佳組卷效果。

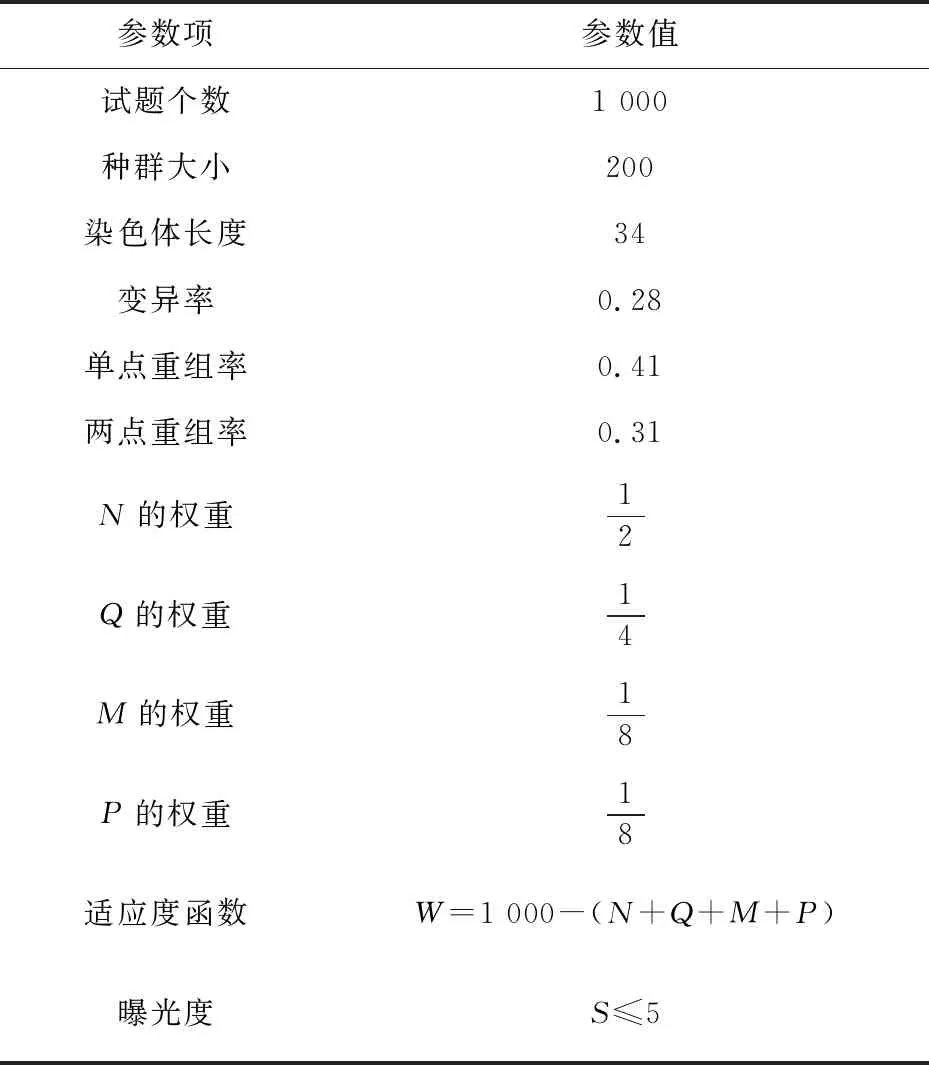
表2 進化中使用的參數

迭代次數與適應度函數的變化如圖5所示。通過圖5可以看出，由于初始化種群時得到的種群比較理想，故開始時最佳適應度函數就已經在980～1 000的范圍內波動，試卷的平均適應度則在870～950的范圍內波動，經過496次迭代后，最佳適應度函數達到1 000，即組卷達到最好效果。

通過試驗輸出的試卷中的試題在題庫中的編號為[538，61，748，683，275，330，50，979，510，774，705，168，945，759，471，589，27，77，835，798，679，454，53，682，663，177，321，158，273，68，691，219，215，806]，也就是說這套試題符合給定的約束條件，該組卷算法成功地完成了組卷任務。

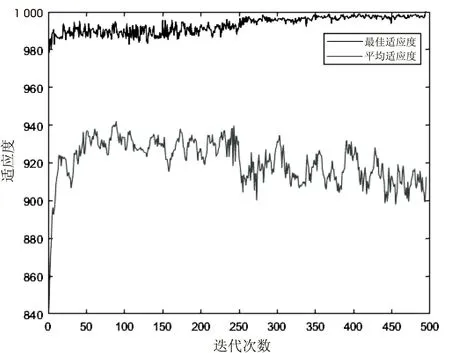
圖5 最佳適應度與平均適應度

5 結束語

通過試驗驗證，基于基因表達式編程算法的智能組卷算法在給定試卷約束條件的前提下，構建出組卷問題的數學模型及相應的適應度函數，便可以很快地計算得到理想的結果，即滿足條件的試卷，能有效地防止“早熟”，且簡單快捷，具有較高的實用價值。