基于SCS模型和新安江模型的雨量預警指標綜合動態閾值對比

俞 彥，張行南,2,3，張 鵬，彭海波，方園皓

(1.河海大學水文水資源學院，江蘇 南京 210098； 2.河海大學水安全與水科學協同創新中心，江蘇 南京 210098；3.水資源高效利用與工程安全國家工程研究中心，江蘇 南京 210098； 4.廣東省水利水電科學研究院，廣東 廣州 510610)

山洪災害突發性強，分布廣，局地性強，動量大，破壞性強，對社會經濟的負面影響越來越顯著。據世界氣象組織統計，全世界受山洪災害影響的國家超過100個。我國山地丘陵區占比較大，夏季短歷時強降雨頻繁，山洪災害問題也較為嚴重，2017年山洪災害經濟損失達2 100億元，洪災死亡人數大約占災害死亡人數64%，構成重大挑戰[1]。

國內外針對降雨閾值的研究方法各有不同。美國構建的Flash Flood Guidance系統[2-3]被廣泛應用于英美等西方國家，該模型充分考慮山洪的致災因素，因此對資料的完整性要求較高。日本因為自然環境條件單一，更加關注雨強大小和歷時長短，提出了匯流時間降雨強度方法和實效雨量法等[4]。澳大利亞在各國山洪災害研究成果的基礎上建立了自己的山洪預警平臺，采用不同顏色表示山洪災害的危險性[5]。我國的山洪災害降雨閾值研究起步較晚，方法由早期的統計學方法向水文模型方法過渡。陳桂亞等[6]基于降雨災害同頻率法計算了降雨閾值；陳瑜彬等[7]通過最小二乘法擬合實測降水量與臨界雨量的函數關系，建立臨界雨量函數；毛北平[8]運用垂向混合模型計算得到無資料地區降雨閾值；樊靜等[9]運用HBV模型計算得到開都河致災洪水臨界雨量；盧燕宇等[10]將TOPMODEL模型與統計方法相結合應用于山洪災害預警。

目前針對雨量預警指標的確定仍以靜態的單一閾值為主，考慮水文過程及山洪災害的特點，但雨量預警指標應考慮下墊面地形、植被等綜合因素以及土壤含水量的動態變化過程。降雨強度并非是誘發山洪的唯一因素[11]，地形、土地利用以及土壤含水量等均對山洪的誘發產生影響。其中地形、土地利用類型等下墊面條件一定程度上決定了流域產匯流機制；而前期土壤含水量的動態變化直接影響降雨入滲、包氣帶蒸散發以及產流等過程，在其他條件相同的前提下，飽和的土壤更易誘發山洪，故在確定流域雨量預警指標時，需考慮地形、土地利用等綜合要素以及土壤含水量動態變化的影響，構建綜合動態閾值。而構建綜合動態閾值的關鍵在于如何反映下墊面條件及土壤含水量動態變化對山洪誘發產生的影響。廣東省地處熱帶和亞熱帶氣候過渡區，臺風和局地強對流天氣常常引發局地強暴雨，且山區面積大，境內嚴重的山洪災害時有發生，是我國山洪災害影響顯著的省份之一，故本文以廣東省具有代表性的典型小流域為研究對象，探求適用于山區小流域降雨預警的方法。

1 流域概況

選取廣東省羅定市具有代表性的典型小流域太平鎮太北村和羅鏡鎮大平崗村作為研究對象，流域水系和高程概況如圖1所示。

羅定市地處廣東省西部，位于兩廣交界處，天氣炎熱且終年雨水豐富，多年平均降水量約為 1 400 mm，雨季為每年的4—10月，夏季暴雨頻繁且降水量大，遠大于蒸發能力。太平鎮太北村和羅鏡鎮大平崗村小流域地處羅定市南部邊陲，兩小流域相鄰，干流均匯入羅定河。其中，太平鎮太北村小流域東西跨度為25.8 km，南北跨度為35 km，面積為383.03 km2，最大高程差為1 196 m，干流比降為13.20‰；大平崗村小流域東西跨度為21.38 km，南北跨度為17.89 km，面積為138.26 km2，最大高程差為1 239.6 m，干流比降為22.18‰。兩者均屬于典型的山地小流域。通過查詢各小流域控制斷面水文流量關系曲線得知，太北村小流域致災水位為89.95 m，臨界流量為1 547.4 m3/s；大平崗村小流域致災水位為89.54 m，臨界流量為607.1 m3/s。

圖1 太北村和大平崗村流域圖

2 研究方法

2.1 臨界產流量推求

臨界產流量是指誘發山地小流域山洪災害對應的產流量。由于山地小流域的坡度較大，山洪多為高含沙水流，加上山地小流域資料不全，目前對山地小流域匯流的研究仍不成熟，對山地小流域的匯流模擬計算仍以匯流曲線為主。采用匯流曲線進行匯流模擬，臨界產流量可通過臨界流量除以匯流曲線的峰值得到：

Rt=Qs/Qp

(1)

式中：Rt為臨界產流量；Qs為臨界流量；Qp為匯流曲線的峰值。

式(1)中，臨界流量Qs一般可根據地區的設計洪水以及河道的行洪標準確定，或根據已發山洪的調查評價資料分析獲得。本文根據當地的致災水位結合斷面水位-流量關系曲線確定臨界流量Qs的取值。

缺資料的山地小流域匯流曲線包括時段單位線、三角匯流曲線等。考慮到山地小流域匯流過程的復雜性，從山洪災害預警的實際出發，選擇三角匯流曲線來模擬山地小流域的匯流過程。三角匯流曲線可靈活反映不同計算步長條件下的匯流過程，在歐美國家應用廣泛。

三角匯流曲線如圖2所示，其主要特征值包括漲水段時間Tp、退水段時間Tr以及匯流曲線峰值Qp等。三角匯流曲線包圍的面積為小流域單位凈雨(即1 mm)所產生的徑流量V，即，

V=0.5λ(Tp+Tr)Qp

(2)

式中λ為單位轉換系數。

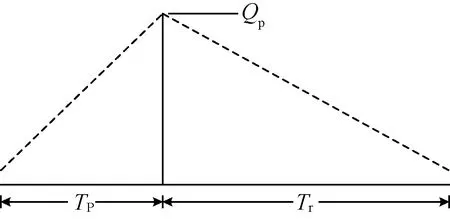
圖2 三角形匯流曲線示意圖

為了得到三角形匯流曲線更加合理的特征值，本文結合廣東省綜合單位線來進行推導。

廣東省綜合單位線是通過研究納希瞬時單位線方法，并汲取國內外經驗，提出的一套具有廣東特色的綜合單位線[12]。《廣東省暴雨徑流查算圖表使用手冊》將整個廣東省劃分為五大區域，每個區域給出了典型的無因次單位線以及該無因次單位線對應的最大縱坐標值um以及一階原點矩K的值。經查，羅定市屬于綜合單位線中的大陸低區，并且采用Ⅲ號無因次單位線，可得到無因次單位線K值：

K=vu1/Tp

(3)

式中：Δt為單位線計算時段，h；m1為單位線滯時，與流域的坡度及匯流路徑等因素有關，h。

《廣東省暴雨徑流查算圖表使用手冊》建立了單位線滯時m1與集水區域特征參數θ的相關關系，參數θ計算公式為

(4)

式中：J為干流平均坡降，‰;L為匯流路徑長度，m。

綜合以上公式，可以推導出三角匯流曲線峰值Qp的數學表達式：

(5)

式中：A為流域面積，km2；系數0.09是通過量綱分析推導出的。

由式(5)可以看出，三角匯流曲線雖然方法較為簡單，但該方法考慮了坡度、匯流路徑以及流域面積等對匯流過程的影響，能反映不同流域下墊面條件對匯流過程的影響，具有可操作性。通過該方法可方便地得到流域的臨界產流量，為綜合動態臨界雨量的推求分析提供基礎。

2.2 雨量綜合動態臨界閾值推求

SCS模型和新安江模型是兩種雨量閾值推求方法。基于SCS模型的推求方法需要考慮的下墊面條件可以綜合反應在同一個參數上，該方法較為簡單，對于山區小流域較合適。基于新安江模型的推求方法主要用到了該模型的蒸散發和產流模塊，其利用蓄水容量分配曲線考慮到了土壤缺水量不均勻問題。本文對比兩種模型在臨界雨量計算上的差異，以確定更適合山區小流域雨量閾值計算的方法。

2.2.1基于SCS模型的推求方法

SCS模型是美國農業部水土保持局于1954年開發的SCS模型，是目前應用最為廣泛的流域水文模型之一[13]。其顯著特點是模型結構簡單、所需輸入參數少,擁有集總式水文模型的優點[14]，是一種較好的小型集水區徑流計算方法，基于SCS模型可以獲得臨界雨量的解析解。

SCS模型基本產流方程為

(6)

式中：P為降水總量，mm；R為產流量，mm；Ia為初損水量，mm；S為流域土壤最大蓄水能力，mm。

結合廣東省羅定市當地實際情況，令Ia=0.2S，則產流方程為

(7)

式中S為與流域前期濕潤狀況、坡度、植被、土壤類型和土地利用現狀等有關的參數，可以通過CN值推求：

(8)

式中VCN為CN值，是SCS模型中的重要參數，它反映下墊面的產流能力[15]，屬于無量綱參數,理論取值范圍是0～100,實際應用中取值范圍是40～98。

本文根據土地利用類型、土壤類型等進行CN值查算。根據質地不同將土壤分為4類[16]，從A類到D類的不同類別的土壤具有如下演變規律：砂土含量逐漸降低，黏土含量逐漸增高，壤土含量在B類和C類中較高；滲透速率和導水速率逐漸降低，土壤的最大蓄水能力也逐漸降低。

式(7)和(8)表明，流域產流量與降水量和土壤最大蓄水能力有關，降水量增大或土壤蓄水能力的減小均使產流量增大；而土壤質地、植被覆蓋、土地利用方式和前期土壤含水量會綜合影響土壤蓄水能力。同時，為了反應前期土壤含水量對CN值的影響，采用以下經驗公式對CN值進行修正：

VCN,dry=4.2VCN/(10-0.058VCN)

(9)

VCN,wet=23VCN/(10+0.13VCN)

(10)

式中：VCN,dry為土壤較干燥情況下的CN值;VCN,wet為土壤較濕潤情況下的CN值。

基于以上兩式可以得到不同土壤含水量條件下的CN值，如圖3所示(VCN,normal為正常土壤含水量情況下的CN值)。

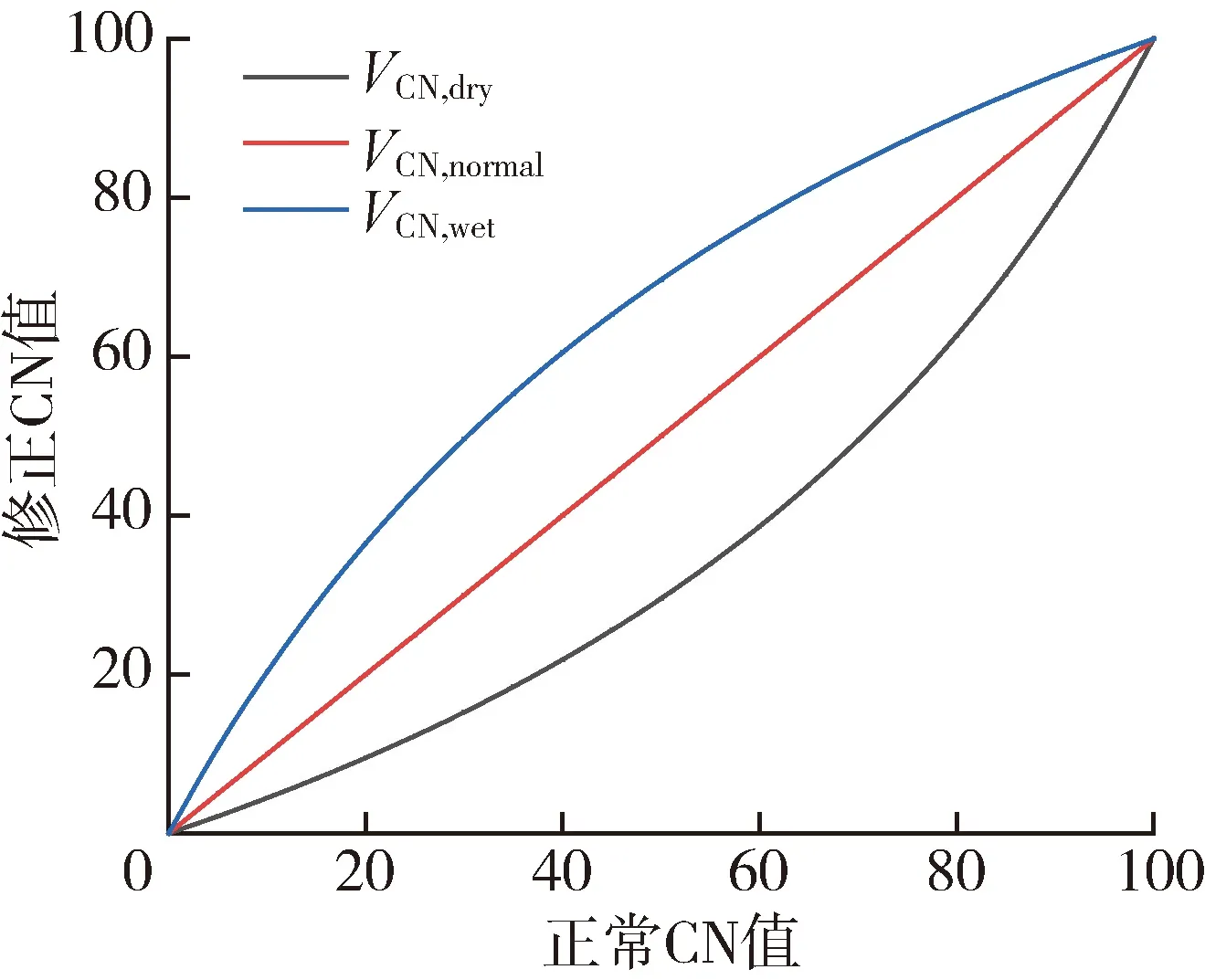
圖3 不同土壤含水量條件下CN值示意圖

通過查詢當地土地利用類型分布圖和土壤質地分布圖，利用加權平均算法，得到兩個研究對象的正常CN值均為86。

在確定不同時段臨界產流量Rt的基礎上，考慮不同前期土壤含水量條件下的流域土壤最大蓄水能力，由式(7)反推可以得到一系列反應流域綜合動態的雨量預警閾值P′的解析解：

(11)

2.2.2基于新安江模型的推求方法

新安江模型是由河海大學趙人俊教授領導的科研團隊提出的模型，因其科學合理的概化、嚴密的模型結構等優勢，能準確地模擬濕潤及半濕潤地區降雨條件下的蓄滿產流及匯流過程，在我國廣大濕潤與半濕潤地區的防洪減災和水資源高效利用方面發揮了重要作用[17-19]。此外，新安江模型在廣東省洪水預報以及防洪調度方面有較好的運用[20]。

考慮到降水和流域下墊面[21]分布不均勻的影響，新安江模型的結構設計為分布式，分為蒸散發計算、產流計算、分水源計算和匯流計算4個層次結構[20]。本文主要采用新安江模型的蒸散發及產流計算部分進行綜合動態臨界雨量的推求。

a. 蒸散發計算。流域蒸散發的計算沒有考慮流域內土壤含水量在面上分布的不均勻性，而是按土壤垂向分布的不均勻性將土層分為3層，用3層蒸散發模型計算蒸散發量。計算公式為

MW=MU+ML+MD

(12)

W=WU+WL+WD

(13)

E=EU+EL+ED

(14)

EP=CKEM

(15)

式中：MW為流域平均張力水容量，mm；MU為流域上層張力水容量，mm；ML為流域下層張力水容量，mm；MD為流域深層張力水容量，mm；W為總的張力水蓄量，mm；WU為上層張力水蓄量，mm；WL為下層張力水蓄量，mm；WD為深層張力水蓄量，mm；E為總的蒸散發量，mm；EU為上層蒸散發量，mm；EL為下層蒸散發量，mm；ED為深層蒸散發量，mm；EP為流域蒸散發能力，mm；CK為流域蒸散發折算系數；EM為蒸發皿測得的蒸散發能力，mm。

b. 產流計算。新安江模型是先計算總徑流量再進行水源劃分，產流計算中采用蓄滿產流。按照蓄滿產流的概念，采用蓄水容量面積分配曲線來考慮土壤缺水量分布不均勻的問題。所謂蓄水容量面積分配曲線是部分產流面積隨蓄水容量而變化的累計頻率曲線。應用蓄水容量面積分配曲線可以確定降雨空間分布均勻情況下蓄滿產流的總徑流量。為計算簡便，假定不透水面積MI=0，其線型為

(16)

式中：f為產流面積，km2；F為全流域面積，km2；W′為流域單點的蓄水量，mm；Wmax為流域單點最大蓄水量，mm；B為蓄水容量面積曲線的指數。

c. 臨界雨量推求。基于新安江模型的臨界雨量推求采用窮舉試錯法進行。以土壤含水量的最大值設置不同的初始土壤含水量條件，針對不同的土壤含水量初始條件，以基于SCS模型推求的臨界值作為初值，以0.1 mm為步長，生成一系列的臨界雨量輸入新安江模型計算，比較新安江模型計算的直接徑流產流量以及臨界產流量，當兩者的差值小于1 mm時，認為對應的雨量為臨界雨量。對所有土壤含水量初始條件重復以上過程，可以得到一系列反應流域綜合動態的雨量預警閾值P。

2.2.3前期土壤含水量推求

上文中構建的綜合動態閾值為不同土壤含水量條件下的閾值，在實際應用中流域尺度上的土壤含水量難以通過觀測直接得到，故本文參考水文預報中的前期影響雨量概念，基于山洪災害預警時段前期的降雨確定土壤含水量的狀態。

前期影響雨量Pa的計算式為

Pa,t+1=Ka(Pa,t+Pt)

(17)

式中：Pa,t,Pa,t+1分別為第t天和第t+1天開始時刻的前期影響雨量，mm；Pt為第t天的流域降水量，mm；Ka為流域蓄水的日消退系數，每個月可近似取一個平均值，等于(1-Em/Wm)，其中Em為流域月平均日蒸散發能力；Wm為流域最大蓄水量，是反映該流域蓄水能力的基本特征。

3 結果與分析

圖4(a)(b)分別為羅定市太平鎮太北村和大平崗村基于SCS模型以及新安江模型分析得到的 1 h、3 h和6 h的綜合動態臨界雨量值。

(a) 太北村

(b) 大平崗村

由圖4可以看出，不論針對哪個研究對象，兩個模型的計算結果均隨前期土壤含水量的增大而減小，表明模型計算符合降雨徑流模擬物理規律。此外，隨著土壤含水量從0%到100%變化，模型計算得出的臨界雨量變化幅度最大為36 cm，這表明前期土壤含水量在小流域山洪預警中起到至關重要的作用，若降雨前土壤較干燥，含水量較小，那么即使是很大的一場降雨，其產流量也會很小；若是降雨前土壤含水量就已經達到飽和狀態，那么即使是很小的一場降雨，也可能會造成山洪災害。

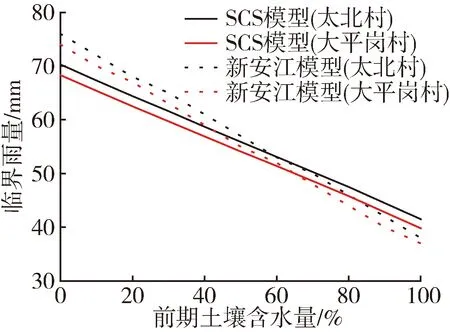
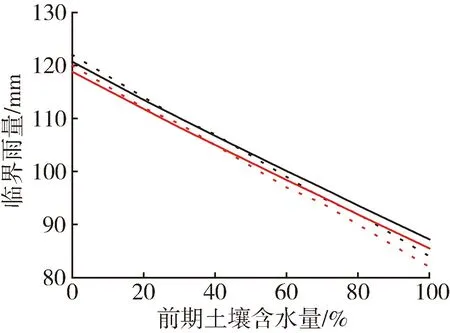
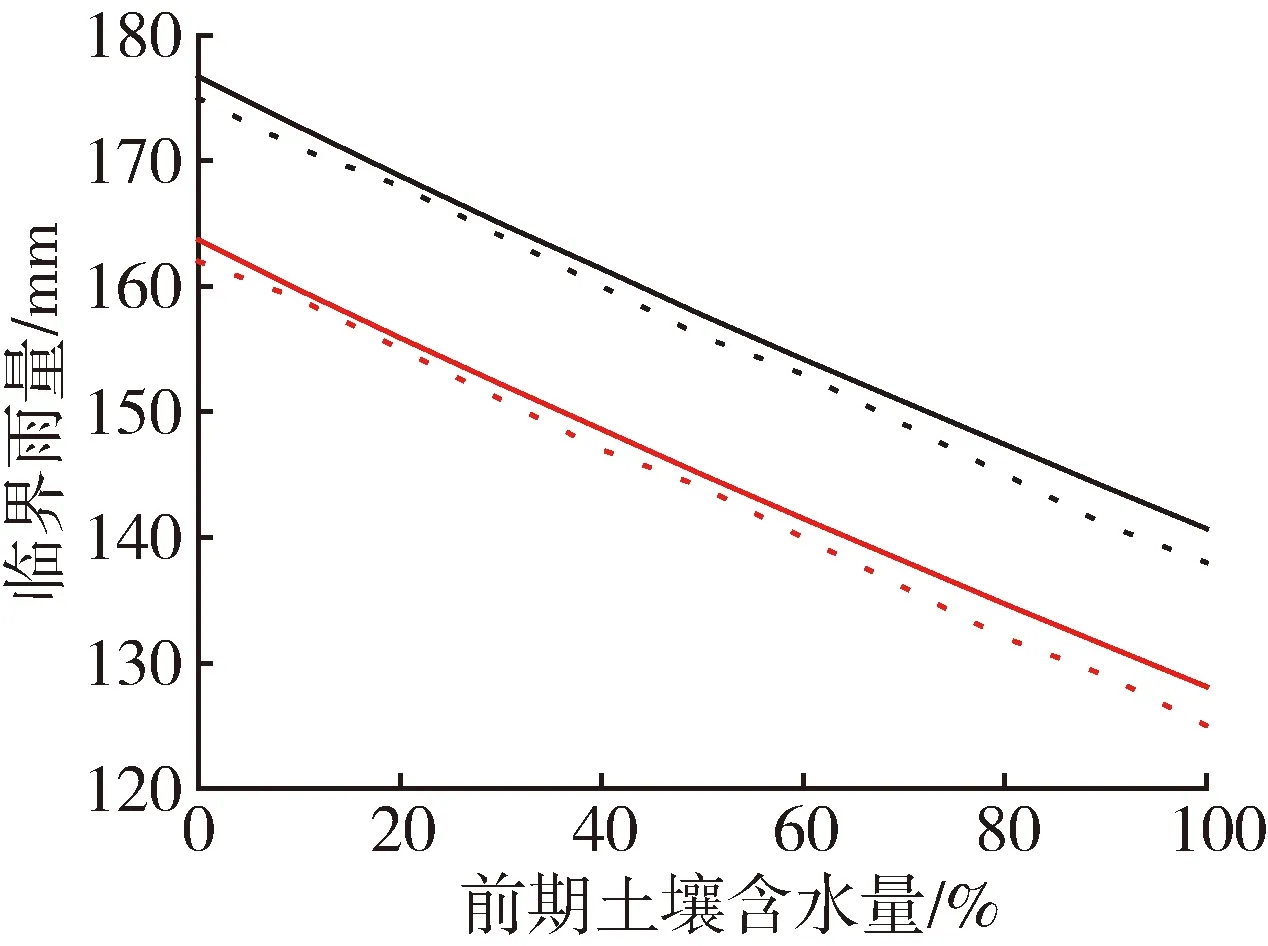
圖5是基于兩個模型推求的太北村和大平崗村相同時段綜合動態臨界雨量值的對比。

(a) 1 h

(b) 3 h

(c) 6 h

由圖5可以看出，兩個模型計算出的綜合動態臨界雨量值存在一定的差異，最大偏差為5.7 mm。對于1 h和3 h的臨界雨量而言，存在某一土壤含水量的臨界值，當土壤含水量高于該臨界值時，基于新安江模型的臨界雨量小于基于SCS模型的臨界雨量；而當土壤含水量低于該臨界值時，基于新安江模型的臨界雨量大于基于SCS模型的臨界雨量。對于6 h臨界雨量而言，雖然由SCS模型推求的臨界雨量大于新安江模型，但是隨著土壤含水量的上升，兩者模擬的結果相差也越來越大。因此總的來說，小流域一場暴雨發生后的較短時期內，若土壤含水量偏干旱，由SCS模型推導得出的臨界雨量較為安全；相反，若土壤含水量偏濕潤，由新安江模型推求的臨界雨量較為安全。這個差異是由SCS模型的基本假定導致的，由于SCS模型認為產流過程中的初損值為定值，并通過流域可能最大滯留量關系導出，而考慮到產流過程的非線性特征，在不同土壤含水量條件下產流的初損值會有差異；另一方面新安江模型則通過指數型的張力水蓄水容量曲線來模擬產流過程，故從物理意義上來講新安江模型更加可靠。

表1為太北村和大平崗村典型小流域的基于SCS模型和新安江模型的雨量預警指標綜合動態閾值與國家標準復核預警指標的對比結果。國家標準復核預警指標是廣東省水利水電科學研究院《廣東省山洪災害調查評價成果復核檢驗》項目中根據國家山洪災害防治組《山洪災害預警指標檢驗復核技術要求》計算的，該預警指標是前期土壤達到飽和狀態時得出的，故采用土壤含水量100%時模型計算的臨界雨量作為對比。

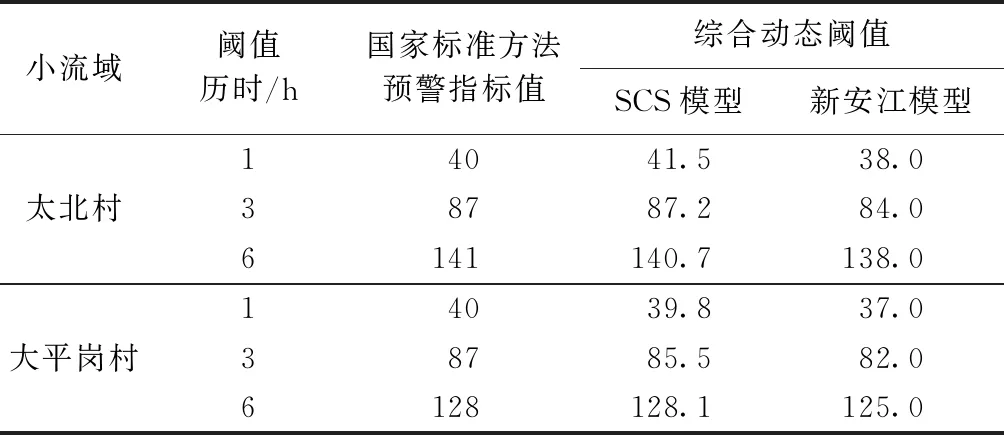
表1 綜合動態閾值成果對比

從對比結果來看，雨量預警指標綜合動態閾值與經國家標準復核后預警指標總體較為接近。基于SCS模型的臨界雨量以及基于新安江模型的臨界雨量均能對山洪過程進行合理預警，其中新安江模型在1 h降雨發生后即可預警，而SCS模型至少在3 h降雨后才達到預警條件。

基于SCS模型推求的降雨閾值比基于新安江模型推求的大。造成該現象的原因是SCS模型的基本假定和兩個模型的原理不同。此外，從山洪災害預警角度來看，基于新安江模型的降雨閾值偏安全，對受災地區的人員、物資轉移更具意義。

4 結 語

SCS模型和新安江模型在臨界雨量的計算上均能滿足預警要求，但新安江模型計算結果在山洪預警中更加可靠。