Nonlinear Degenerate Anisotropic Elliptic Equations with Variable Exponents and L1 Data
KHELIFI Hichemand MOKHTARI Fares
1Department of Mathematics and Informatics,University of Algiers,Algiers,Algeria.2 Street Didouche Mourad Algiers.
2Applied Mathematics Laboratory,Badji Mokhtar University-Annaba B.P.12,Algeria.
Abstract.This paper is devoted to the study of a nonlinear anisotropic elliptic equation with degenerate coercivity,lower order term and L1 datum in appropriate anisotropic variable exponents Sobolev spaces. We obtain the existence of distributional solutions.
Key Words:Sobolev spaces with variable exponents;anisotropic equations;elliptic equations;L1 data.
1 Introduction
In this paper we prove the existence of solutions to the nonlinear anisotropic degenerate elliptic equations with variable exponents,of the type
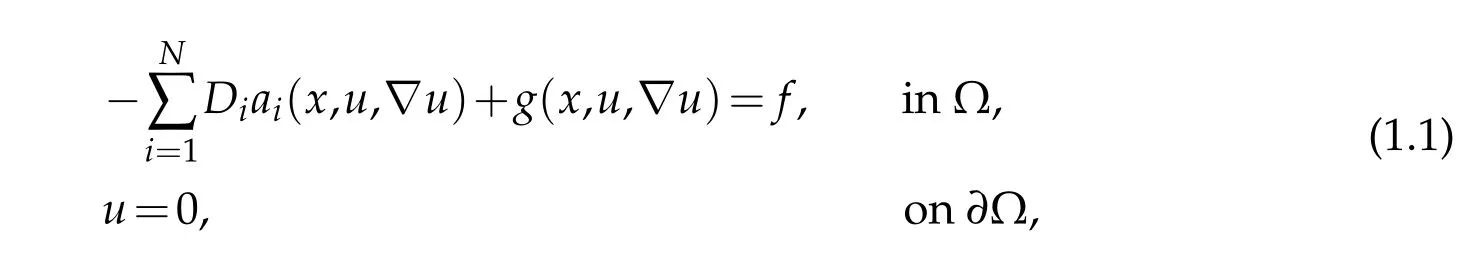
where Ω?RN(N ≥3)is a bounded domain with smooth boundary?Ω and the righthan d sidefinL1(Ω),We suppose thatai:Ω×R×RN →R,i=1,...,Nare Carathéodory functions such that for almost everyxin Ω and for every(σ,ξ)∈R×RNthe following assumptions are satisfied for alli=1,...,N
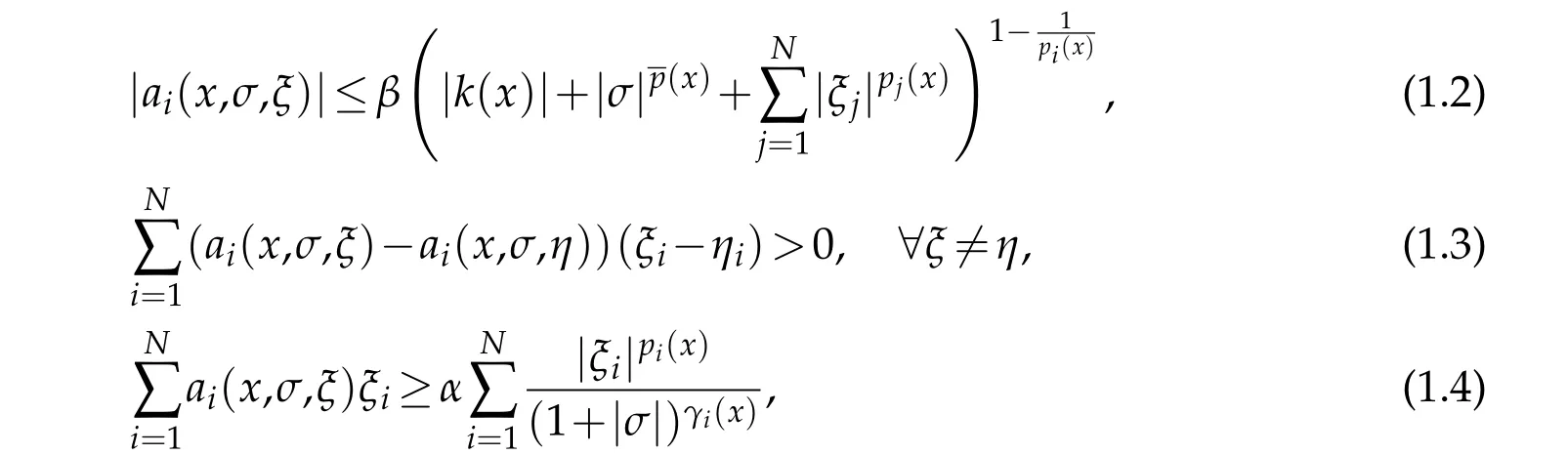
whereβ >0,α >0,and(1,+∞)are continuous functions andis such that
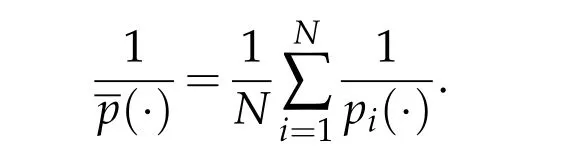
We introduce the function
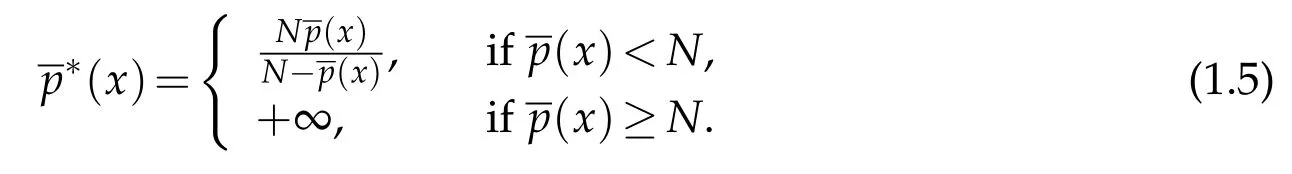
The nonlinear termg:Ω×R×RN →R is a Carathéodory function such that for a.e.x∈Ω and all(σ,ξ)∈R×RN,we have

whereb:R+→R+is a continuous and increasing function with finite values,c ∈L1(Ω)and?ρ>0 such that:
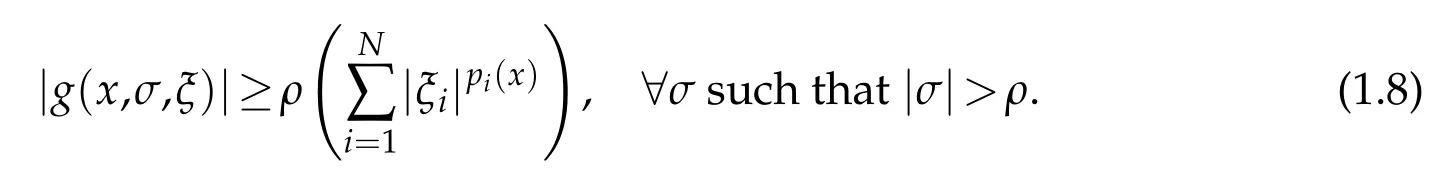
In[1],the authors obtain the existence of renormalized and entropy solutions for the nonlinear elliptic equation with degenerate coercivity of the type
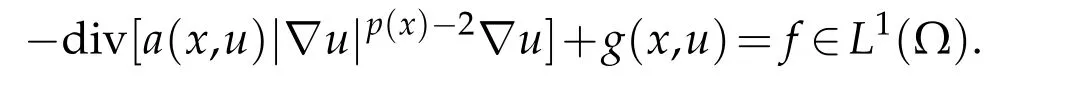
Forg ≡0 andf ∈Lm(·)(Ω),withm(x)≥m-≥1,equation of the from(1.1)have been widely studied in[2],where the authors obtain some existence and regularity results for the solutions.Ifg≡|u|s(x)-1u,
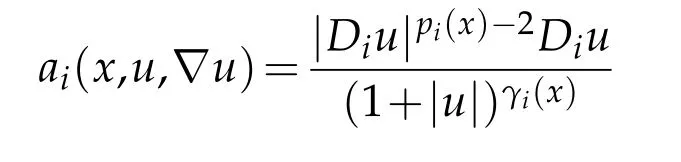
andf ∈Lm(Ω),withm ≥1,existence and regularity results of distributional solutions have been proved in[3].
As far as the existence results for our problem(1.1)there are three difficulties associated with this kind of problems.Firstly,from hypothesis(1.2),the operator
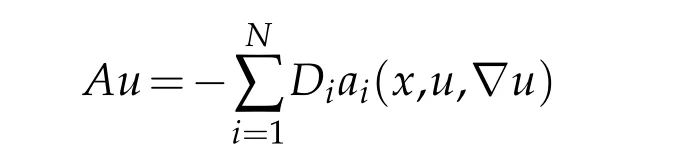
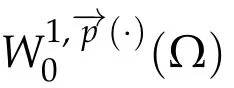
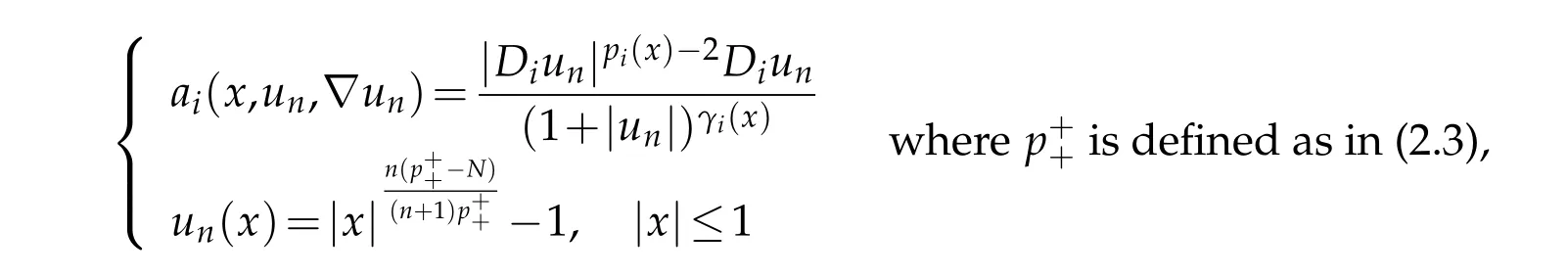
the operatorAis not coercive.Because,iftends to infinity then
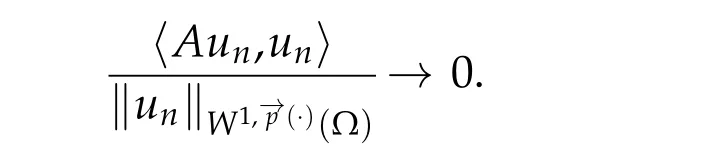
So,the classical methods used in order to prove the existence of a solution for(1.1)cannot be applied. The second difficulty is represented in the fact thatg(x,u,?u)can not be defined frominto its dual,but fromintoL1(Ω). The third difficulty appears when we give a variable exponential growth condition(1.2)forai. The operatorApossesses more complicated nonlinearities;thus,some techniques used in the constant exponent case cannot be carried out for the variable exponent case.For more recent results for elliptic and parabolic case,see the papers[4–8]and references therein.
The paper is organized as follows.In Section 2,we present results on the Lebesgue and Sobolev spaces with variable exponents both for the isotropic and the anisotropic cases,and state the main results.The proof of the main result will be presented in Section 3.We start by giving an existence result for an approximate problem associated with(1.1).The second part of Section 3 is devoted to proving the main existence result by using a priori estimates and then passing to the limit in the approximate problem.
2 Preliminaries and statement of the main result
2.1 Preliminaries
In this sub-section,we recall some facts on anisotropic spaces with variable exponents and we give some of their properties.For further details on the Lebesgue-Sobolev spaces with variable exponents,we refer to[9–11]and references therein.Let Ω be a bounded open subset of RN(N ≥2),we denote
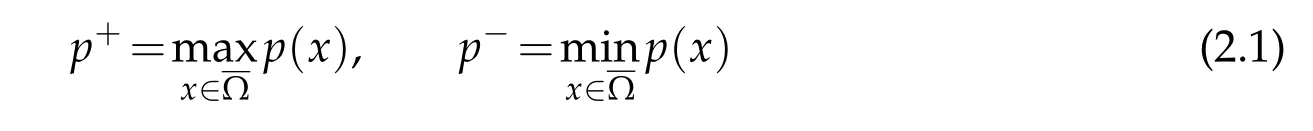
and
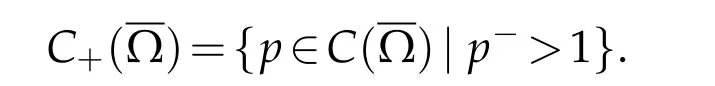
LetWe define the space
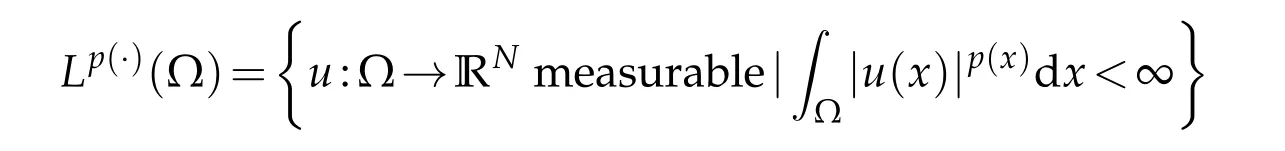
then the expression
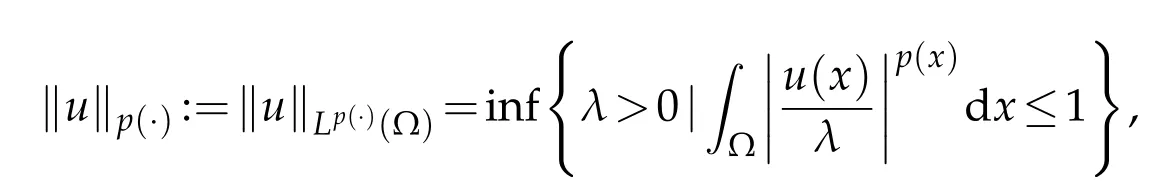
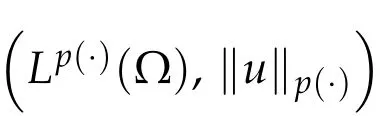
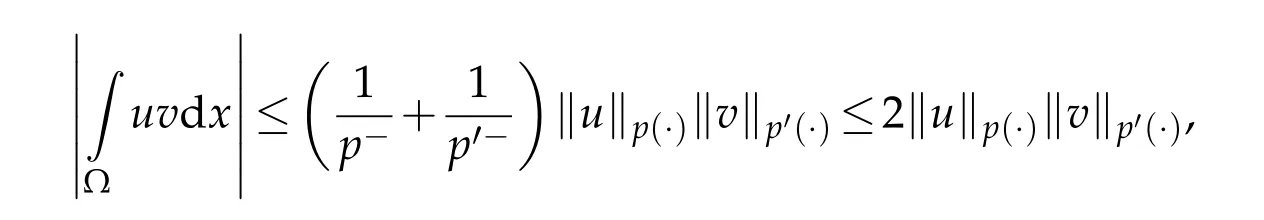
holds true.We define the variable exponents Sobolev spaces by
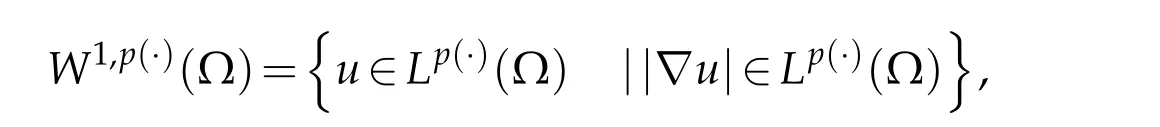
which is a Banach space equipped with the following norm
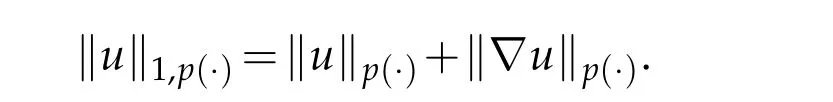
Next,we defineas the closure ofinW1,p(·)(Ω). Finally,we introduce a natural generalization of the variable exponents Sobolev spacesthat will enable us to study with sufficient accuracy problem(1.1).Letwhereare continuous functions.We introduce the anisotropic variable exponents Sobolev spaces
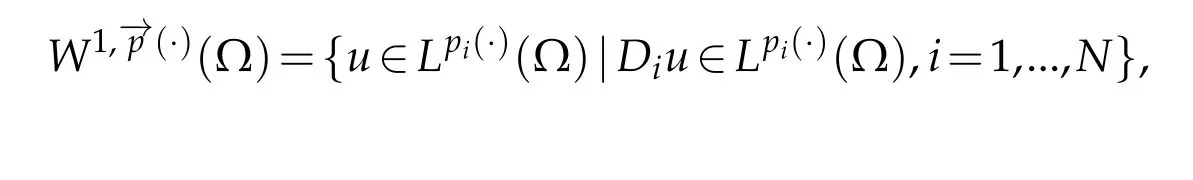
with respect to the norm
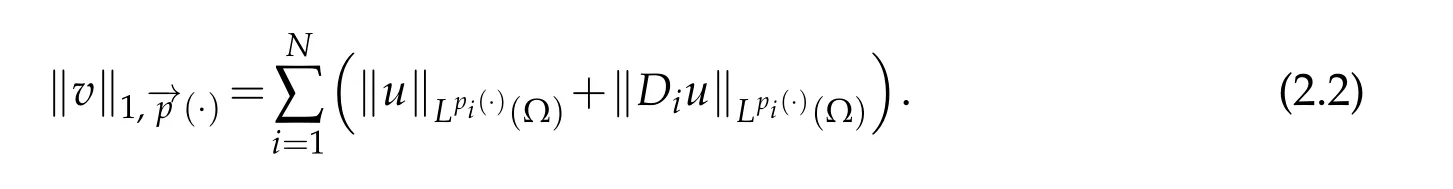
We introduce the following notationas
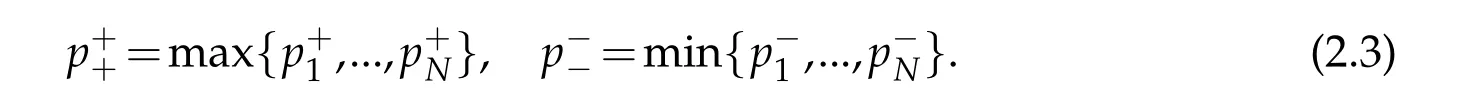
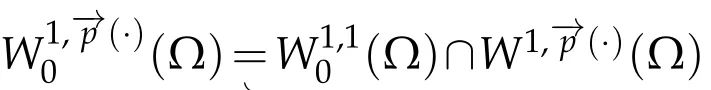
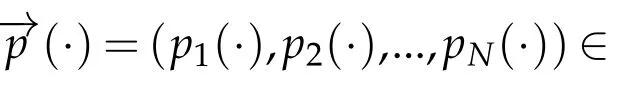
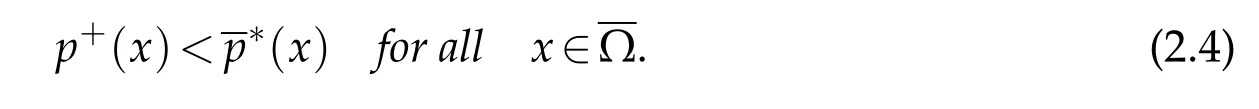
Then
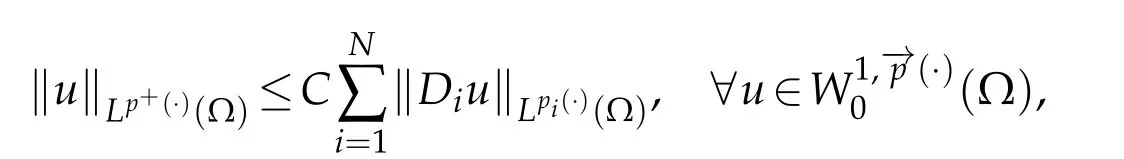
where p+is defined as in(2.1)(1.5),and C is a positive constant independent of u.Thusis an equivalent norm on
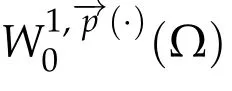
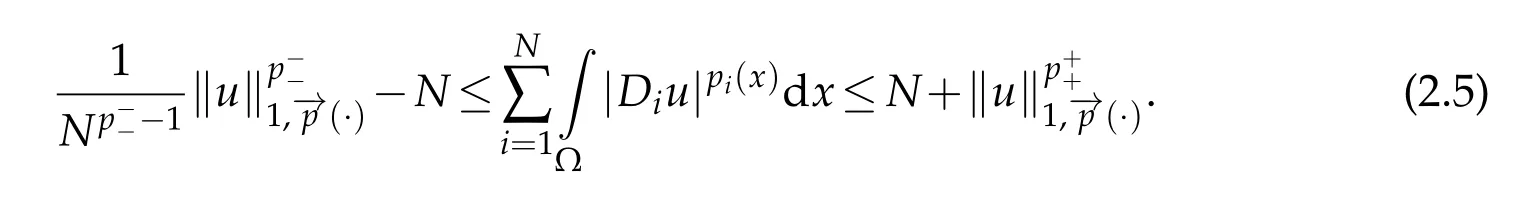
Proof.Put
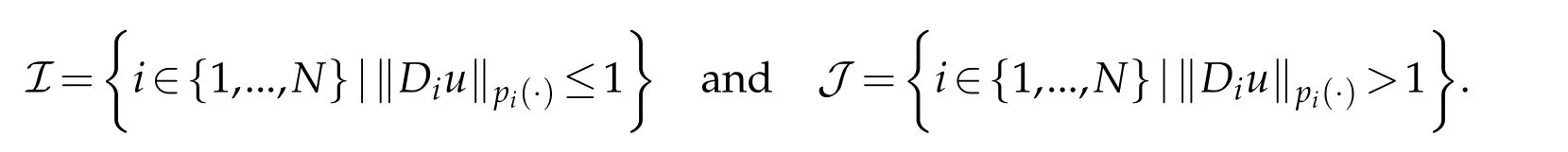
Thanks to(Proposition 2.1 in[3]),we have
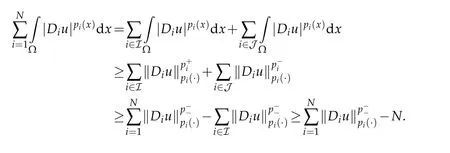
Using the convexity of the applicationwe obtain
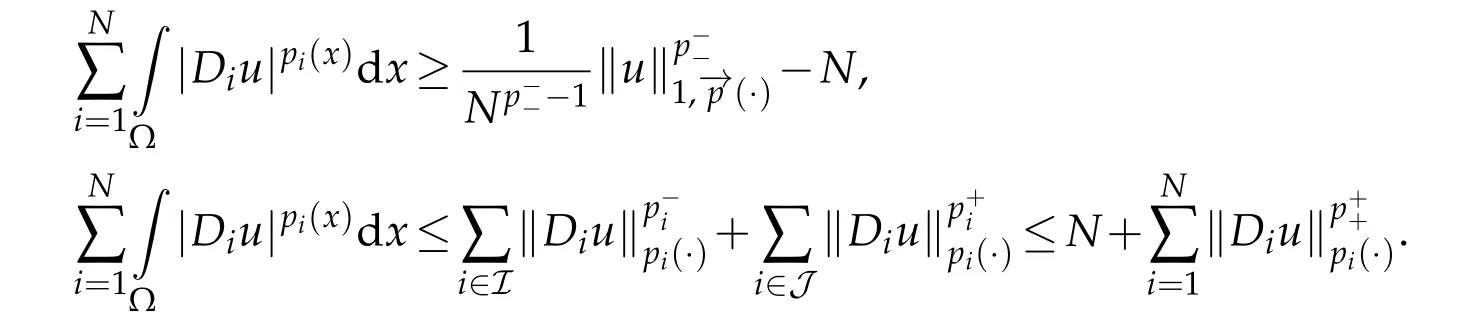
We will use through the paper,the truncation functionTkat heightk(k >0),that isTk(s):=max{-k,min{k,s}}.
Lemma 2.1([12]).Let g∈Lp(·)(Ω)and gn∈Lp(·)(Ω)with‖gn‖p(·)≤C.If gn(x)→g(x)almost everywhere inΩ,then gn ?g in Lp(·)(Ω).
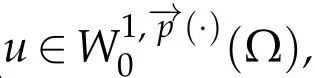
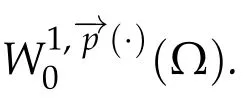
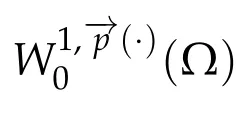
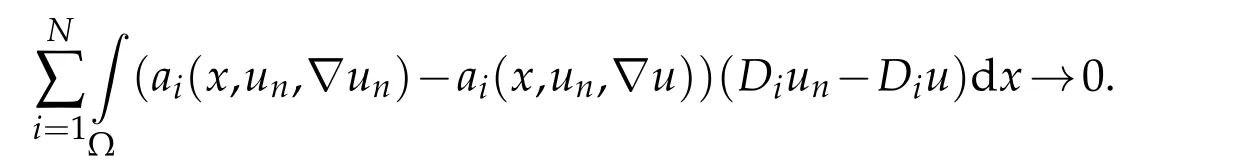
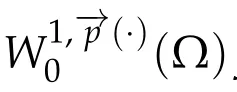
2.2 Statement of main result
We will extend the notion of distributional solution,see[12,13],to problem(1.1)as follows:
Definition 2.1.Let f ∈L1(Ω)a measurable function u is said to be solution in the sense of distributions to the problem(1.1),if
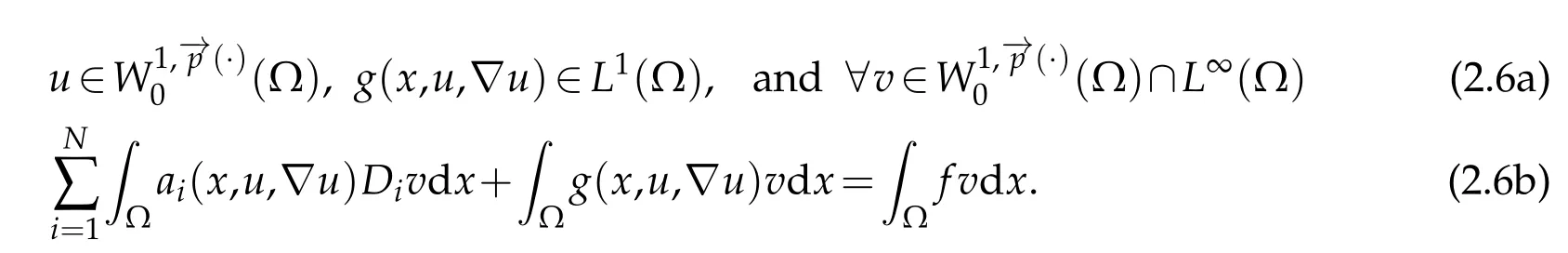
Our main result is as follows
Theorem 2.2.Let f ∈L1(Ω).Assume(1.2)-(1.8)and(2.4).Then problem(1.1)has at least one solution in the sense of distributions.
3 Proof of the main result
3.1 Approximate solution
Let(fn)nbe a sequence inL∞(Ω)such thatfn →finL1(Ω)with|fn|≤|f|(for examplefn=Tn(f))and we consider the approximate problem
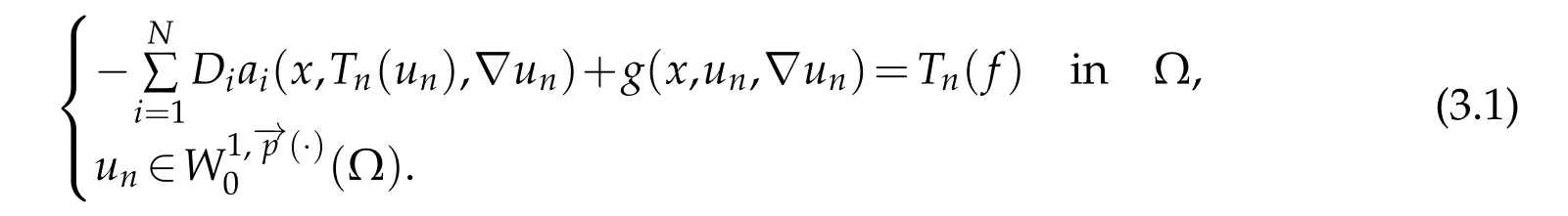
Lemma 3.1.Let f ∈L1(Ω).Assume(1.2)-(1.8)and(2.4).Then,problem(3.1)has at least one solution in the sense of distributions.
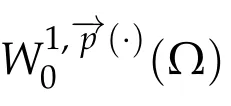
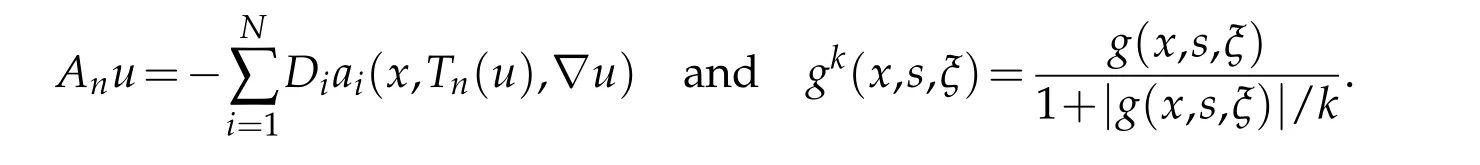
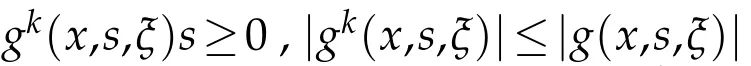
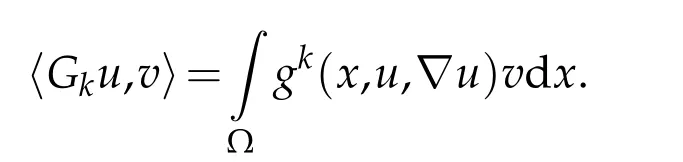
Consider the following problem
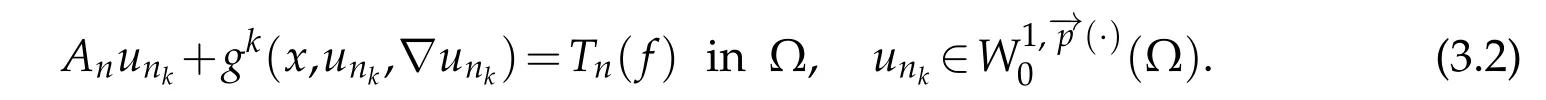
Lemma 3.2.Let f ∈L1(Ω).Assume that(1.2)-(1.8)and(2.4)hold,then the problem(3.2)has at least one solution unk in the sense of distributions.
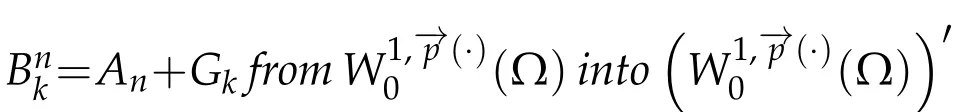
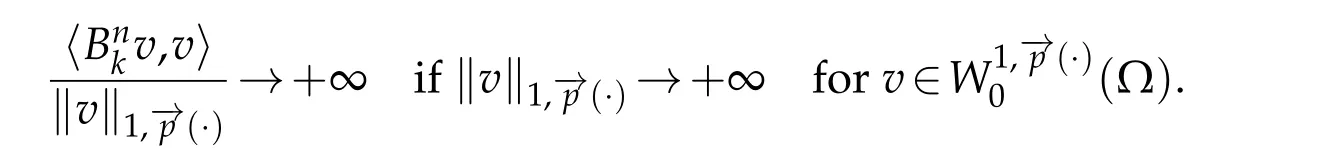
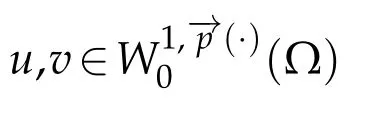
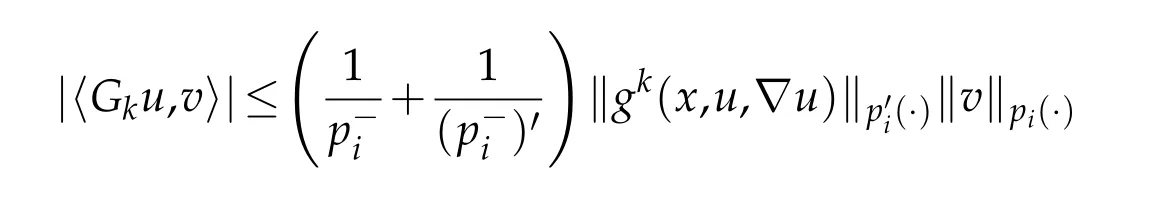
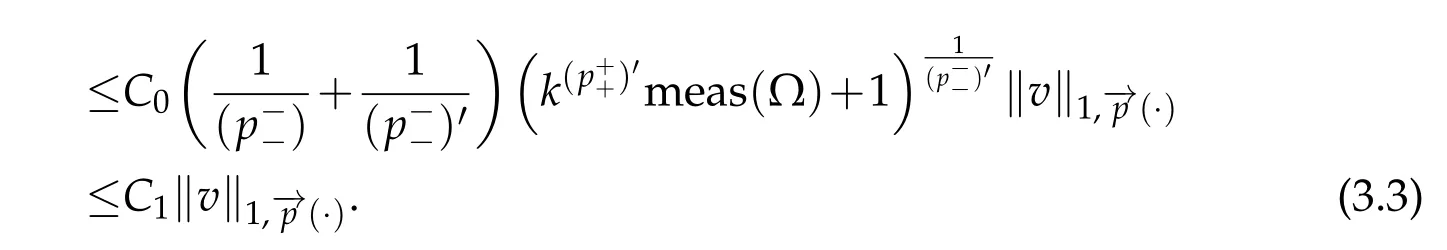
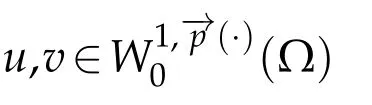
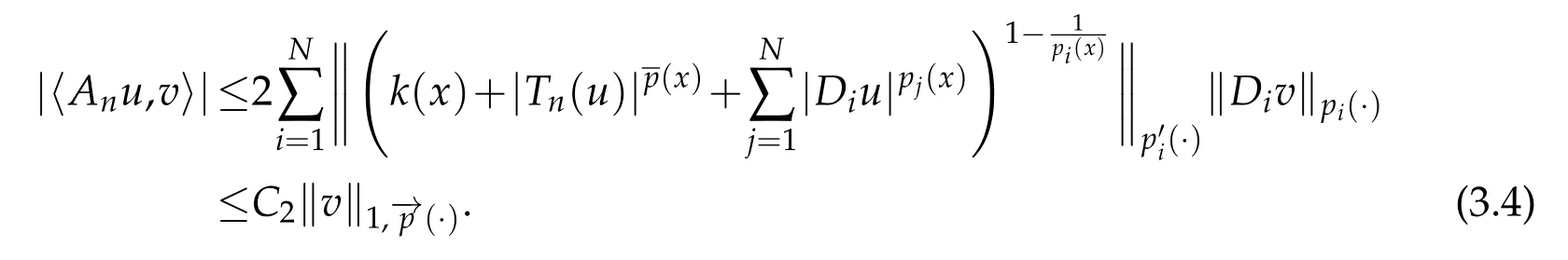
Then by using(3.3)and(3.4)we conclude thatis bounded.For the coercivity,by using(1.4),(1.7),and(2.5),we get
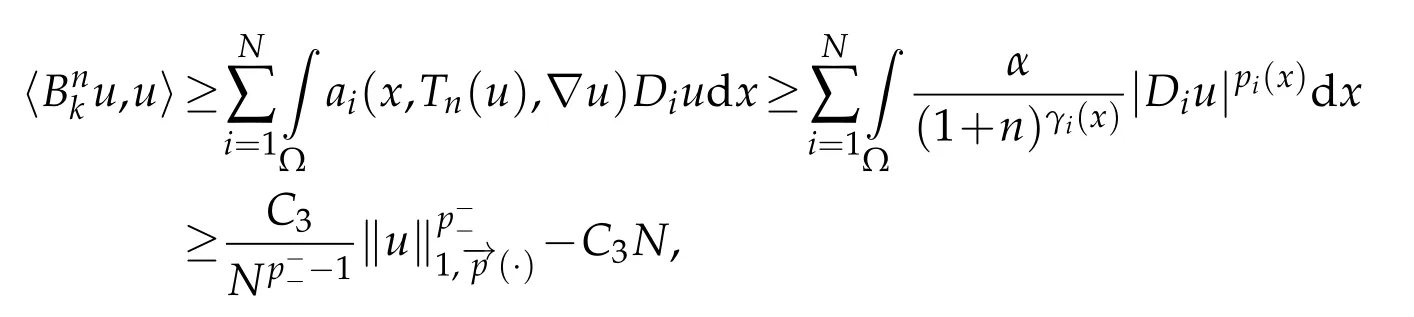
then
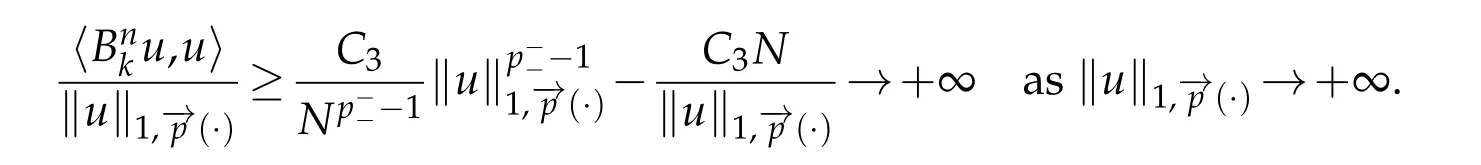
It remains to show thatis pseudo-monotone.Let(um)mbe a sequence insuch that
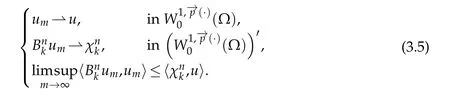
We will prove that
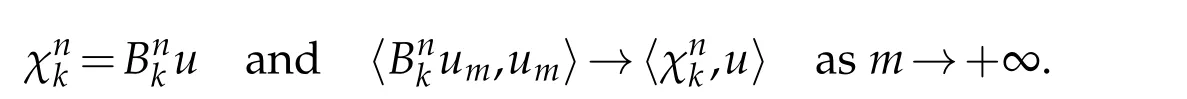
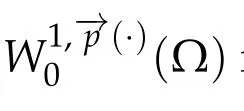

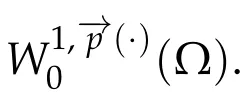
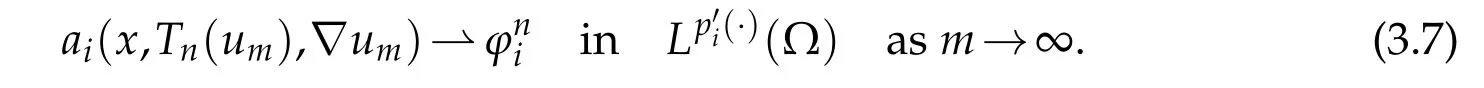
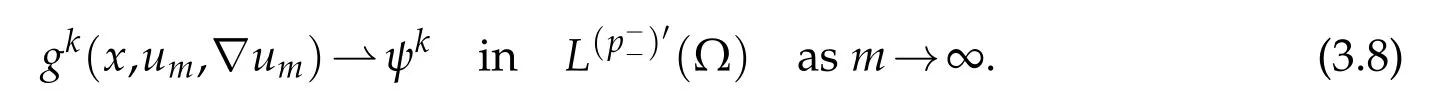
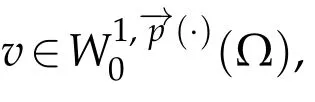
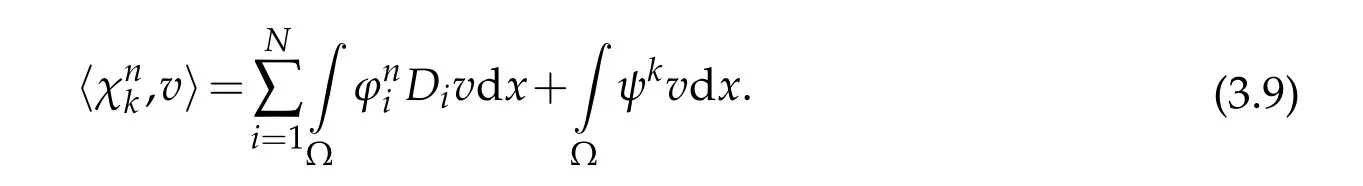
Using(3.5),(3.8),(3.9),and thatum →uinwe have
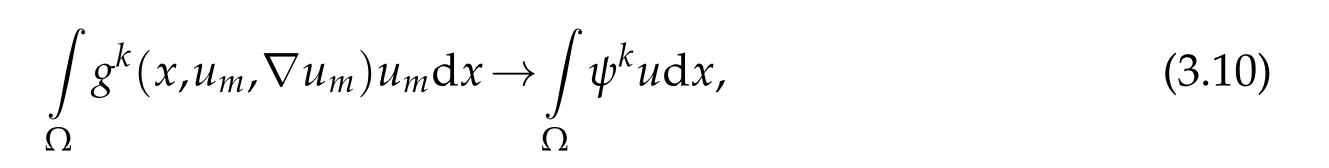
therefore,thanks to(3.5),(3.9),and(3.10),we write
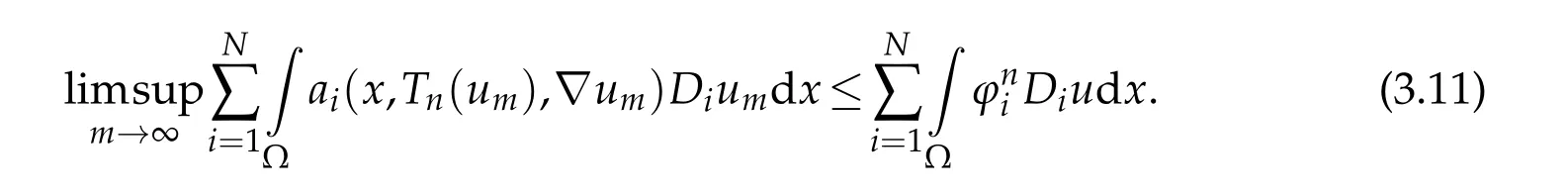
On the other hand,by(1.3),we obtain
在刑事訴訟過程中,檢察機關(guān)天生擁有比被告人更為強大的公訴權(quán),處于絕對的優(yōu)勢地位。如果檢察機關(guān)的這種天生的權(quán)力不受到外部程序控制的話很容易被濫用。庭前會議制度擁有對公訴權(quán)進行司法審查與控制的功能,能夠有效地防止檢察機關(guān)濫用公訴權(quán),可以把一些不符合起訴條件的案件排除在審判程序之外,對進入審判程序的案件起到一個篩選和過濾的功能。
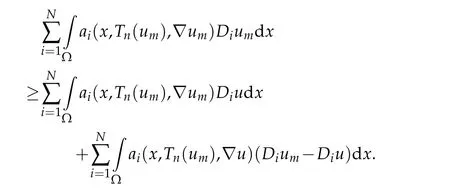
In view of Lebesgue dominated convergence theorem and(3.6),we have
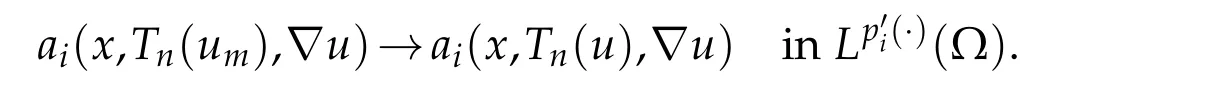
By(3.7)and(3.5),we get
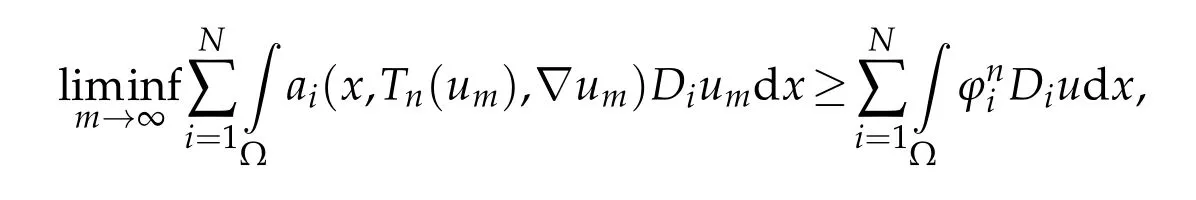
this implies,thanks to(3.11),that
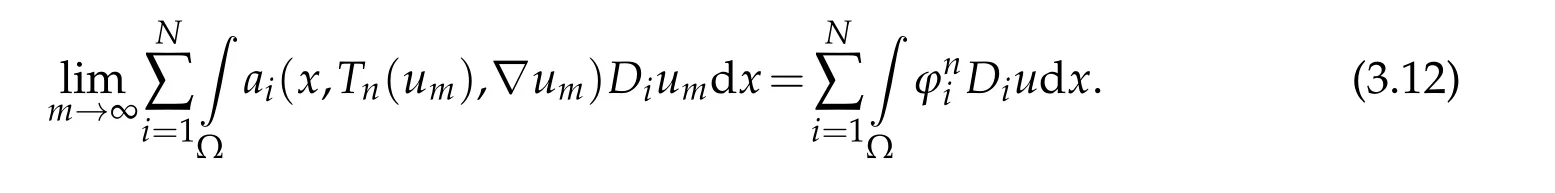
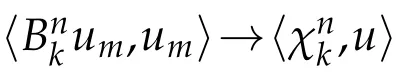
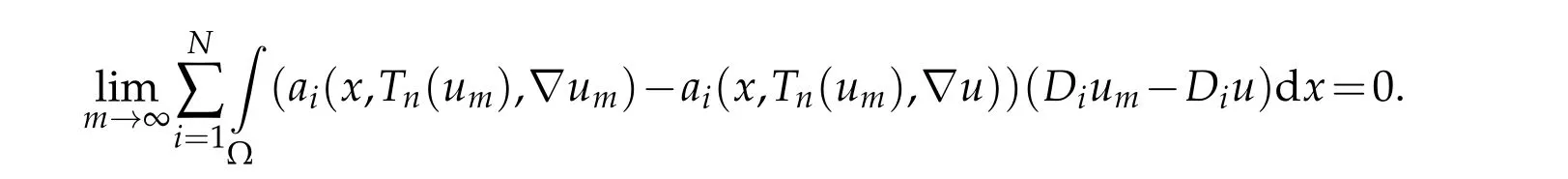
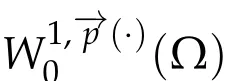
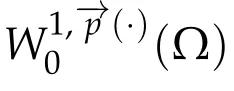
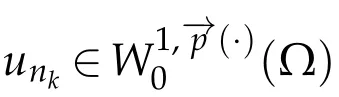
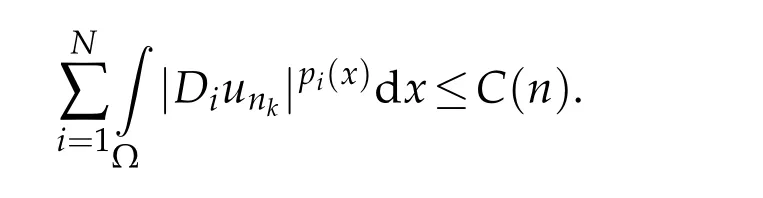
Proof.The proof uses the same technique as in(Lemma 4.1 of[3])and is omited here.
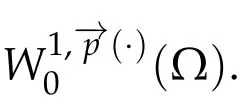
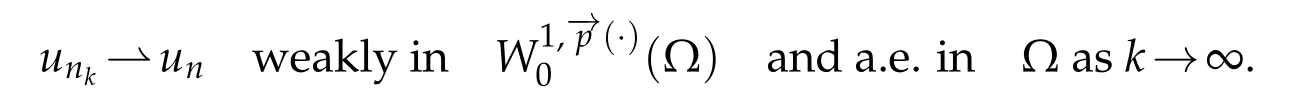
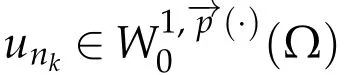
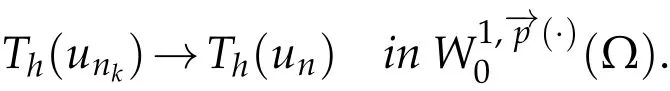
Proof.It is similar to the proof of Theorem 4.2 of[13].
3.2 A priori estimates
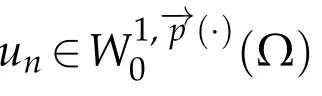
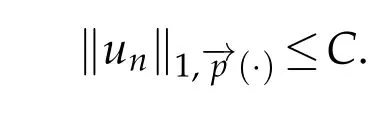
Proof.Leth>0.TakingTh(un)as a test function in(3.1),then
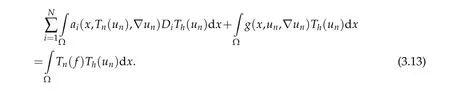
By dropping the nonnegative term in(3.13),(1.7),and(1.4)we get

then
Consequently,
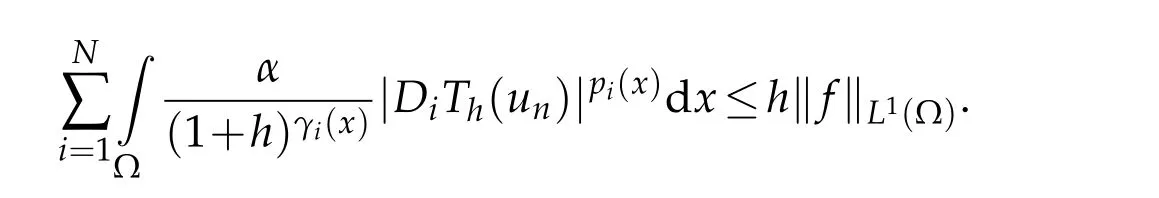
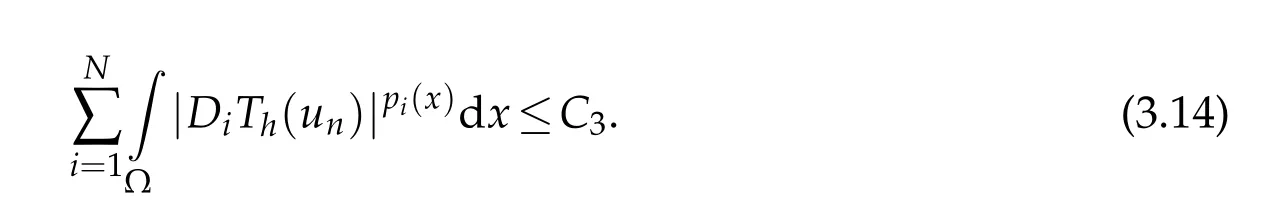
TakingTh(un)as a test function in(3.1),and dropping the first nonnegative term in the left-hand side,we obtain
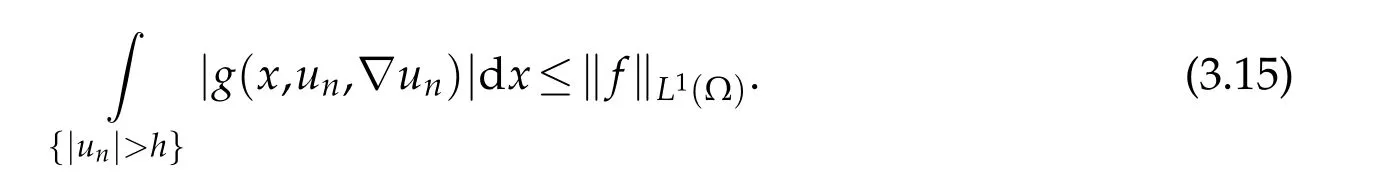
By combining(1.8),(3.14)and(3.15),forh=ρ,we deduce that
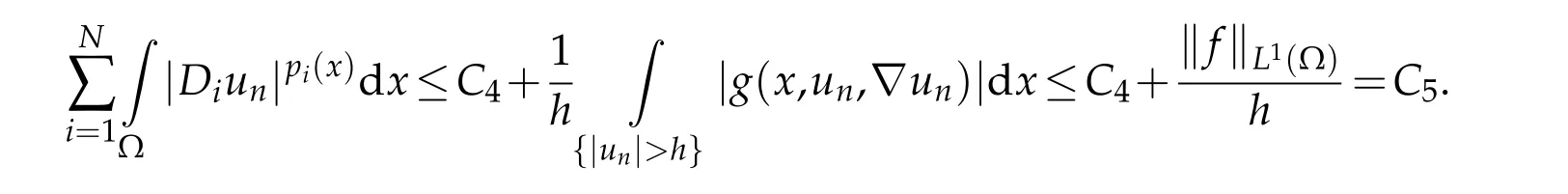
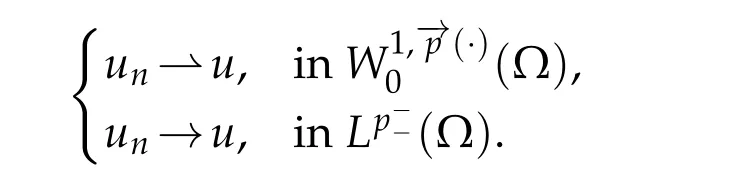
This ends the proof of Lemma 3.6.
3.3 The strong convergence of the truncation
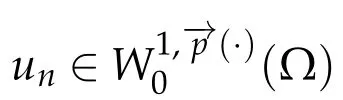
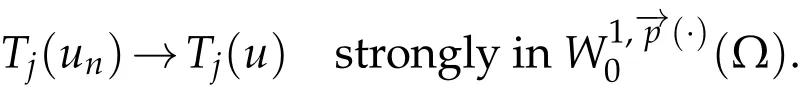
Proof.Leth ≥j >0 andwn=T2j(un-Th(un)+Tj(un)-Tj(u)).We setφj(s)=s·exp(δs2),whereδ=(l(j)/(2α))2,l(j)=b(j)(1+|j|)γ++,and
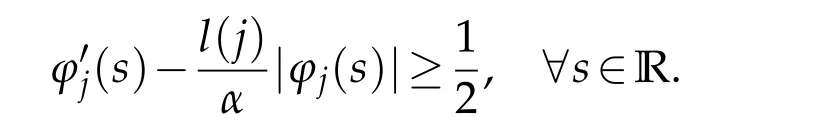
LetM=4j+h.SinceDiwn=0 on{|un|>M}andφj(wn)has the same sign asunon the set{|un|>j}(indeed,ifun >jthenun-Th(un)≥0 andTj(un)-Tj(u)≥0,it follows thatwn ≥0).Similarly,we show thatwn ≤0 on the set{un <-j}.
By takingφj(wn)as a test function in(3.1),we obtain
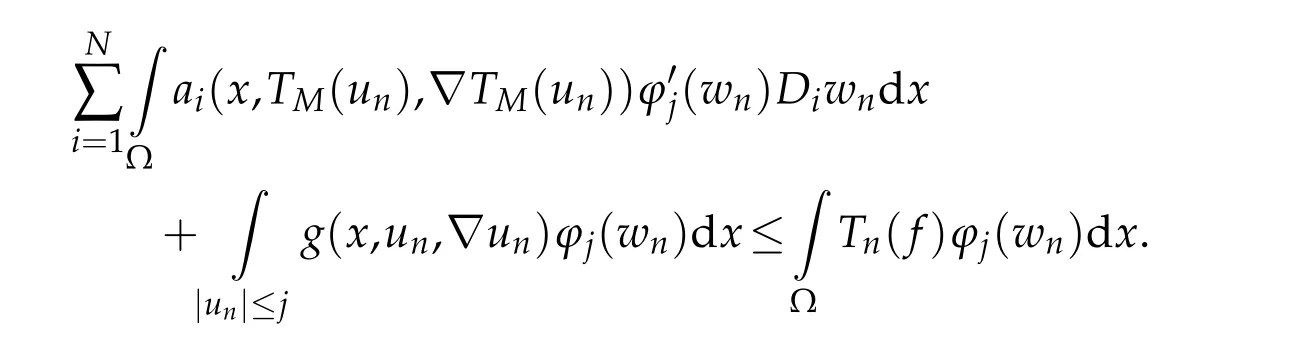
Takingyn=un-Th(un)+Tk(un)-Tk(u),we have
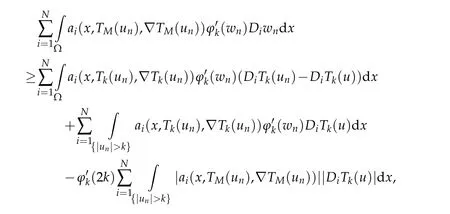
that is equivalent to
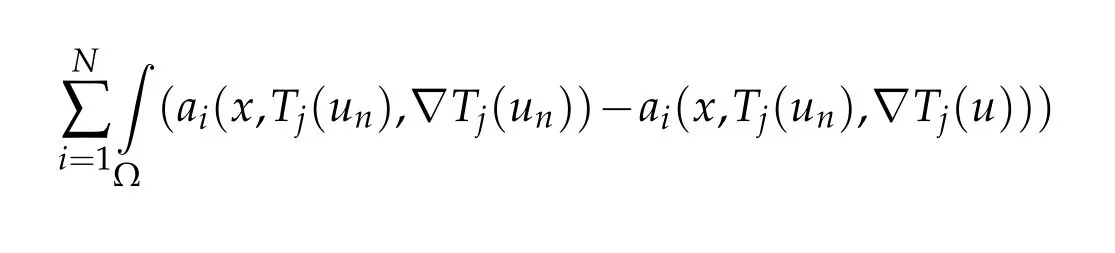
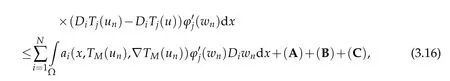
where
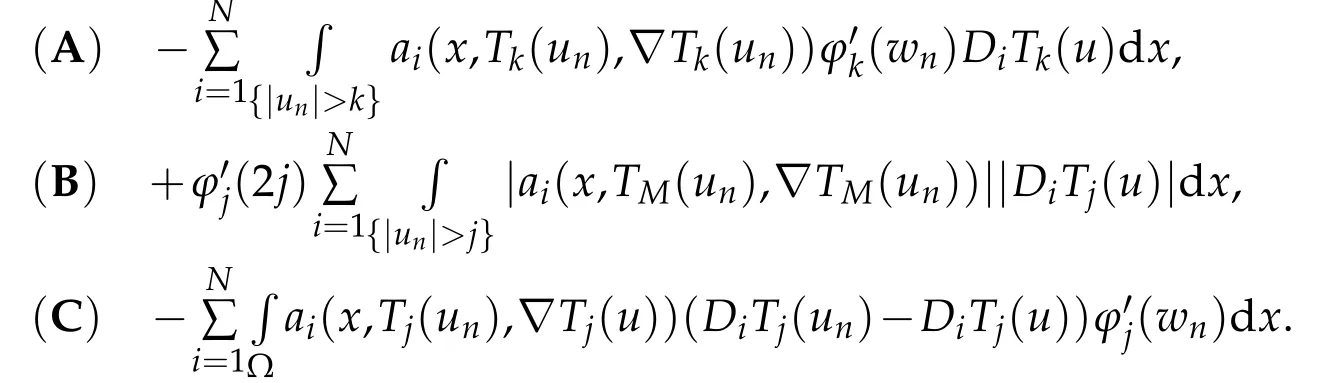
Arguing as in[13],we can prove that
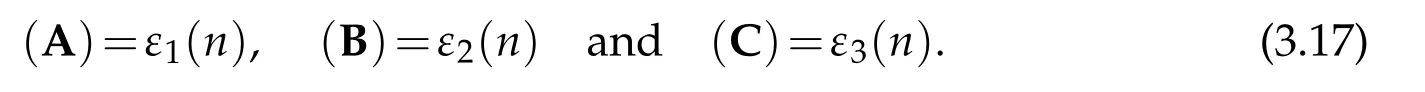
By(3.16)and(3.17)we conclude that
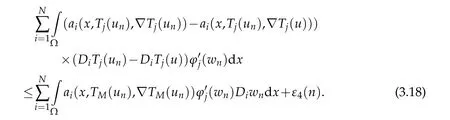
Using(3.18)and arguing as in[13],we get
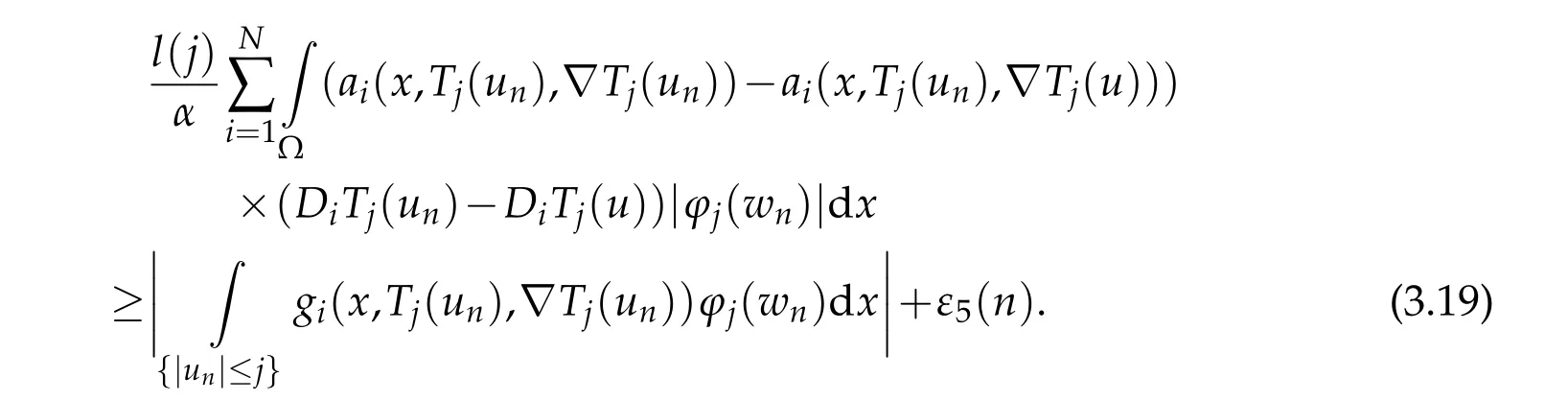
Thanks to(3.18)and(3.19),we obtain
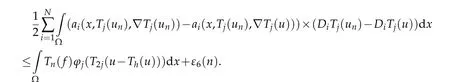
Then by lettinghtends to infinity in the previous inequality,we get
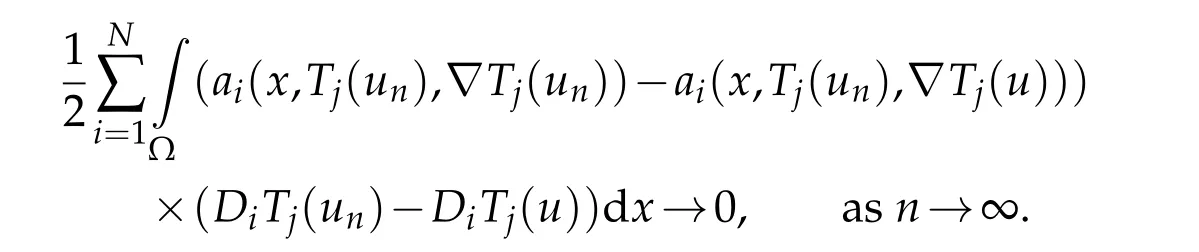
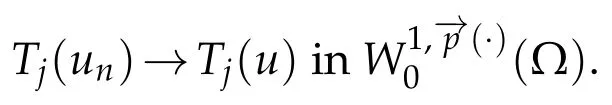
Thanks to Lemma 2.2,we obtain
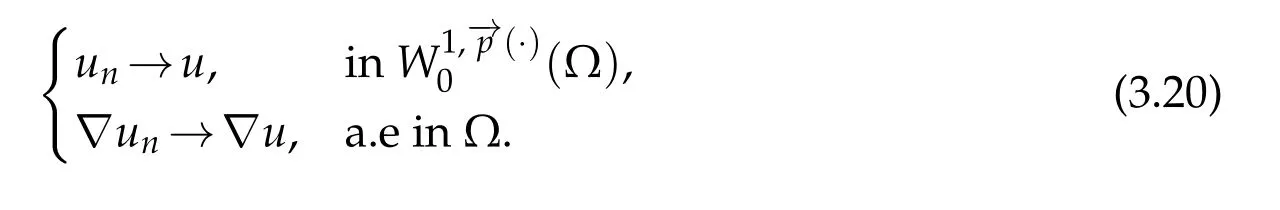
3.4 The equi-integrability of g(x,un,?un)and passage to the limit
Thanks to(3.20),we have
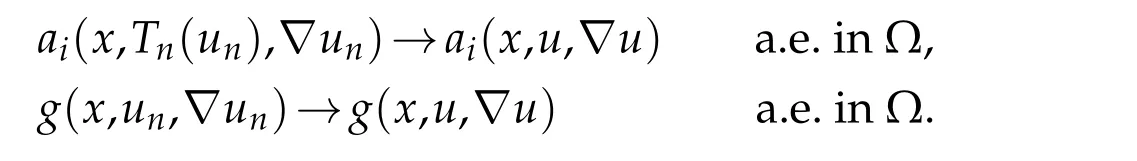
Using that(ai(x,un,?un))nis bounded in,and Lemma 2.1,we obtain
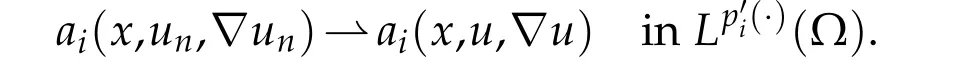
Now,letEbe a measurable subset of Ω.For allm>0,we have by using(1.6)
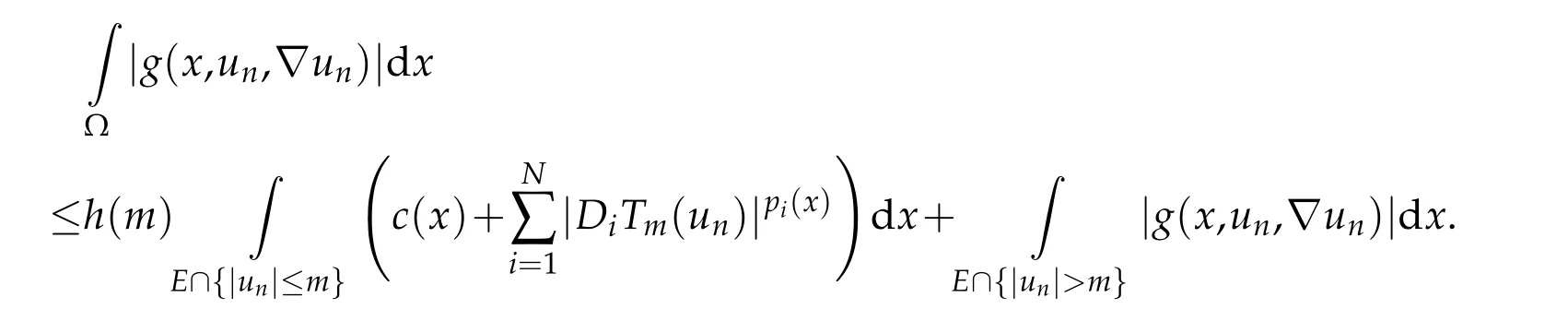
Since(DiTm(un))nconverges strongly inthen for allε>0,there existsδ>0 such thatmeas(E)<δand
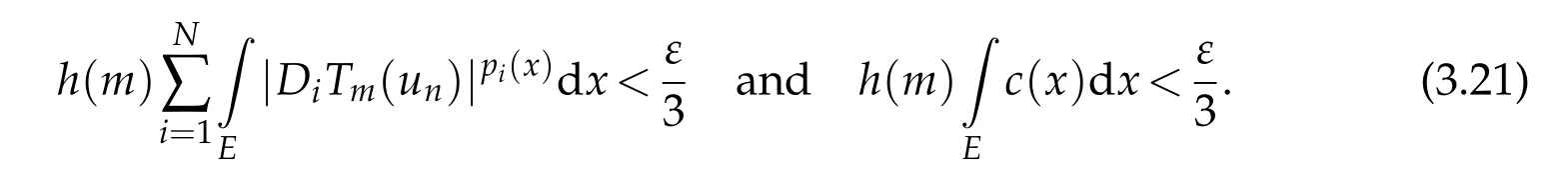
On the other hand,usingT1(un-Tm-1(un))as a test function in(3.1)form>1,we obtain
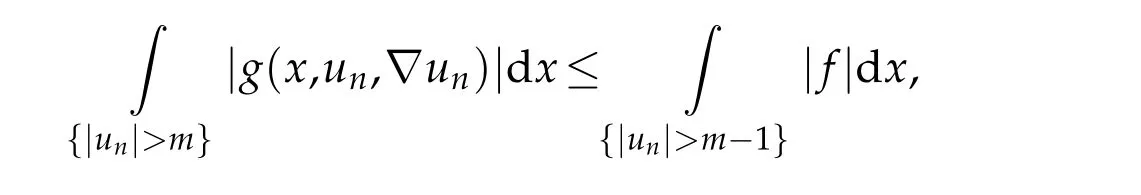
there existsm0>0 such that
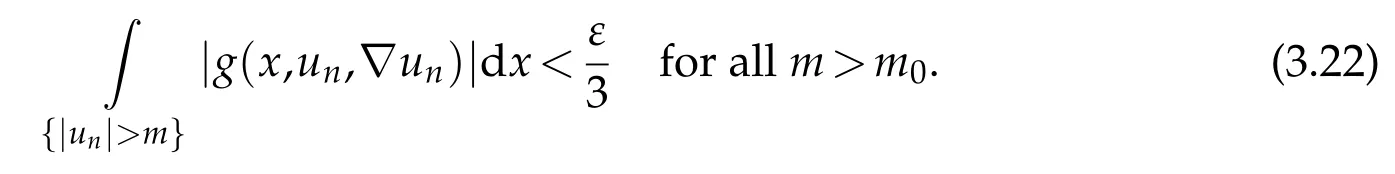
Using(3.21)and(3.22),we deduce the equi-integrability ofg(x,un,?un).In view of Vitali’s theorem,we obtain
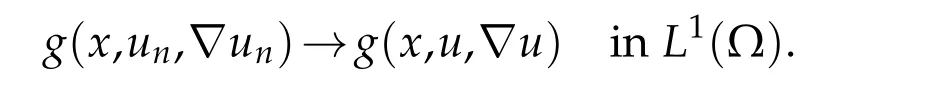
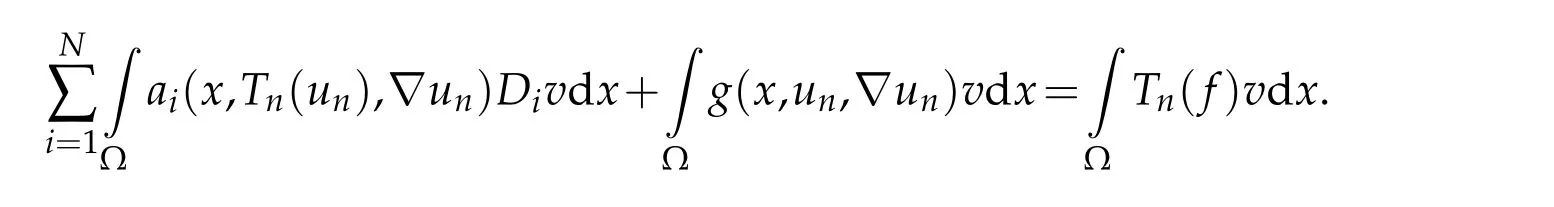
Lettingn →+∞,we can easily pass to the limit in this equation,to see that this last integral identity is true foruinstead ofun.This proves Theorem(2.2).
Example 3.1.As a prototype example,we consider the model problem
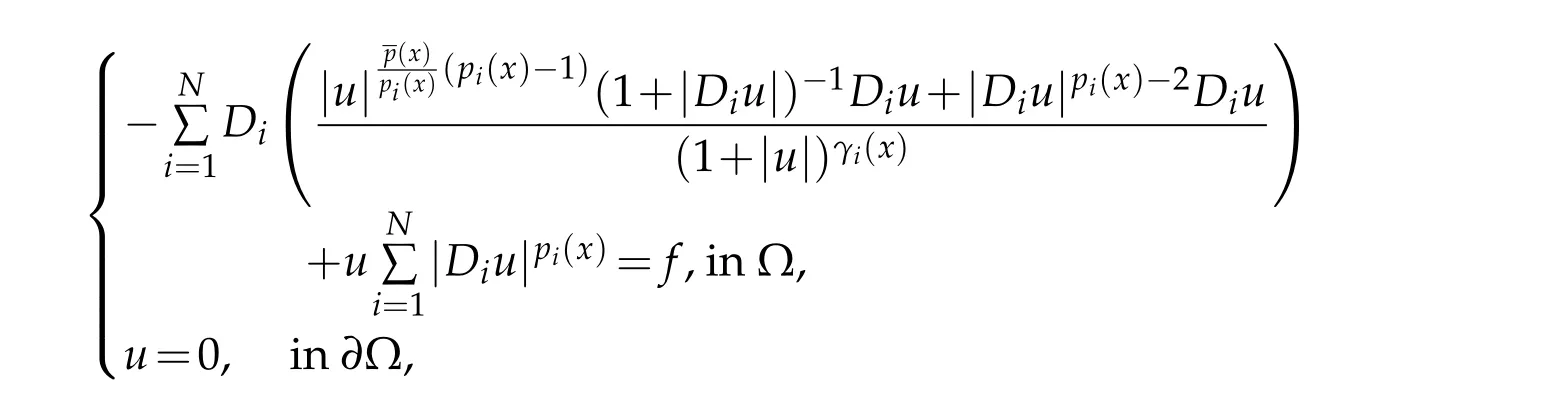
wheref ∈L1(Ω)andas in Theorem 2.2.
Acknowledgments
The authors would like to thank the referees for the useful comments and suggestions that substantially helped improving the quality of the paper.
 Journal of Partial Differential Equations2020年1期
Journal of Partial Differential Equations2020年1期
- Journal of Partial Differential Equations的其它文章
- Explicit H1-Estimate for the Solution of the Lamé System with Mixed Boundary Conditions
- Eigenvalues of Elliptic Systems for the Mixed Problem in Perturbations of Lipschitz Domains with Nonhomogeneous Neumann Boundary Conditions
- Quenching Time Estimates for Semilinear Parabolic Equations Controlled by Two Absorption Sources in Control System
- Gradient Estimates for a Nonlinear Heat Equation Under Finsler-geometric Flow
