模糊測度的零連續性

譚潯曉，張承坤，徐鶴萍，李軍

(中國傳媒大學數據科學與智能媒體學院，北京 100024)

1 引言

1954 年，法國數學家G.Choquet提出了容度(capacity)的概念，定義了一種基于容度的非線性積分，現稱為Choquet積分[4]。1974年日本學者Sugeno提出了模糊測度和模糊積分的概念[16]，用于模糊數學中的模糊評判。所謂Choquet容度或模糊測度是通過公理定義在某個集合系統上的一類特殊的集合函數，不要求可加性。因此，它是概率測度的推廣，在不同領域分別被稱為容度、模糊測度、非可加測度、單調測度和非可加概率等，見文獻[4]，[5]，[12]，[14]，[16]和[17](本文中我們將統稱為模糊測度)。上世紀七十年代以來，模糊測度的研究日益受到人們的重視。特別是近二十多年，人們在模糊測度和相應的非線性積分研究領域取得了豐富成果(見文獻[5]，[6]，[7]，[10]，[15]和[17])。

由于模糊測度失去了經典測度(或概率)理論中賴以生存的可加性，因此，經典測度理論中的許多結果在模糊測度理論中已不再成立。為了將經典測度理論中的結果推廣到模糊測度情形，需要對模糊測度附加一些新的結構，即討論具有一些特殊結構特性的模糊測度，如：次可加性、超可加性、上(下)連續性、序連續性、零可加、弱零可加、上(下)自連續性和正則性等。在一定的條件下，經典測度的許多重要結果在模糊測度空間上得到了有效的推廣(見文獻[5]，[6]，[7]，[10]，[15]，[17]，[20])。

基于模糊測度的非線性積分，如Choquet積分[4]，Sugeno積分[16]，Shilkret積分[15]，泛積分(參見文獻[19]，Sugeno積分和Shilkret積分是它的特例)以及近幾年引入的凹積分[7]是幾類重要的非線性積分。對這些積分的研究人們也取得了豐碩的成果。經典勒貝格積分的基本性質和許多重要定理也被推廣到了非線性積分理論中(見文獻[6]，[7]，[14]，[17])。

本文中，我們將進一步討論模糊測度的零連續性，它是與上(下)連續性、序連續性和上(下)自連續性不同的結構特性。我們給出一些例子說明模糊測度的零連續性與其它幾個常見的結構特性，如：上(下)連續性、序連續性、零可加性和弱零可加性之間的關系。我們將看到模糊測度的零連續性是比下連續性更弱的一個條件。我們將要證明：如果模糊測度是零連續的，那么上述的積分的唯一性對于一般的泛積分(從而對于Sugeno積分和Shilkret積分)和Choquet積分也是成立的。因此，先前得到的相關結果得到了進一步推廣。最后，我們利用可測函數的收斂性刻畫模糊測度的零連續性，給出零連續性的幾個等價條件。

2 預備知識

f=0a.e.于A(當X=A時，簡記為f=0a.e.)；如果μ({x∈X：f=+∞}∩A)=0，則稱f在A上幾乎處處有限，記作f<∞a.e.于A(當X=A時，簡記為f<∞a.e.)。

(1)若μ(φ)=0且μ(X)>0；

在許多文獻中，模糊測度也被稱為容度、單調測度、非可加測度或非可加概率。

我們陳述以下一些概念(參見文獻[5][9][14][17]).

模糊測度μ稱為

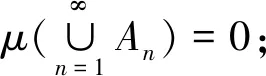
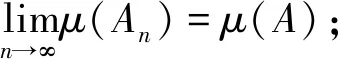
當⊕=+，即泛加法等于通常的算術加法時，上述“次泛可加”、“泛可加”和“σ-泛可加”分別退化為經典測度論中的次可加、有限可加和σ-可加概念。

明顯地，單調測度的零可加性和可數弱零可加性均蘊含著弱零可加性；σ-泛可加性蘊含著泛可加性和可數弱零可加性。

性質2.1如果μ是次泛可加的，那么μ是零可加的，從而μ也是弱零可加的。

μ(A∪B)≤μ(A)⊕μ(B)

=μ(A)⊕0

=μ(A).

另一方面，由μ的單調性μ(A∪B)≥μ(A)，故

μ(A∪B)=μ(A).

因此μ是零可加的。

性質證畢。

性質2.2如果μ是σ-泛可加的，那么μ是下連續的。

證明：與經典測度相應結論的證明類似。

3 模糊測度的零連續性

下面我們回顧模糊測度的零連續的概念(參見文獻[1])。

以下例子說明不是每個單調測度都是零連續的。

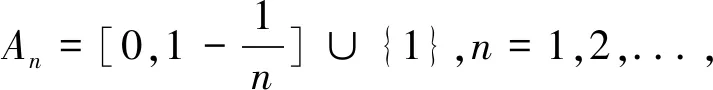
明顯地，我們有以下性質

性質3.1如果模糊測度μ是下連續的，那么μ是零連續的。

然而性質3.1的逆命題不一定為真。以下例子說明單調測度的零連續條件確比下連續條件弱。

例3.2設X=(自然數集)，=(X)，令定義μ：→[0，1]如下：

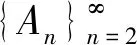
的當且僅當μ同時是零連續和弱零可加的。

由性質2.2可得：

性質3.2如果模糊測度μ是零連續的，那么模糊測度μ就是弱零可加的。

性質3.3如果μ是σ-泛可加的，那么μ是零連續的。從而μ的σ-泛可加性蘊含著μ的零連續性。

性質3.4[1]如果μ是弱零可加和強序連續的，那么μ是零連續的。

性質3.5如果μ是零可加和序連續的，那么μ是零連續的。

注1.以下例子說明強序連續性和弱零可加性沒有必然的蘊含關系。

例3.3設X=(自然數集)，=(X)，令定義集函數μ：→[0，1]如下：

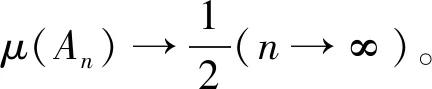
不難看出，上述例3.3中的單調測度μ是零連續的(從而，由性質3.2可知μ是可數弱零可加的)。注意μ不是強序連續的；同時注意到例3.1中的單調測度μ不是零連續的，但不難驗證它是強序連續的。即說明零連續性和強序連續性沒有必然的蘊含關系。

注2.零連續性與弱零可加性沒有必然的蘊含關系。

例3.4設X=(自然數集)，=(X)，定義定義單調測度μ：→[0，1]，如下：

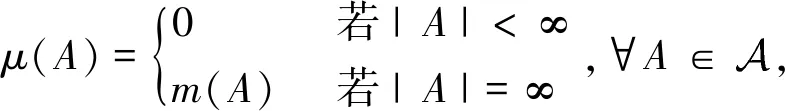
其中符號|A|表示集合A中元素的個數。容易看出μ是弱零可加的。不難驗證，單調測度μ不是零連續的。

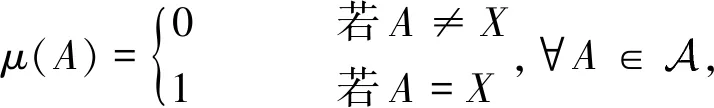
那么μ是零連續的。但μ不是弱零可加的(從而也不是零可加的)。

注3.零連續性與零可加性也沒有必然的蘊含關系。

下面我們回顧最優測度的概念(參見文獻[7]).

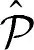
μ(A∪B)≥μ(A)⊕μ(B).

性質3.7μ是零連續的當且僅當μ⊕是零連續的。

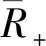
4 泛積分的唯一性

下面我們回顧非負可測函數的泛積分的定義.

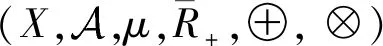
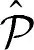
和Shilkret積分[15]：

泛積分有以下基本性質(可參見文獻[11][13][17][18]).

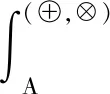
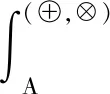
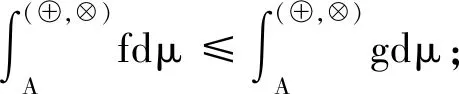
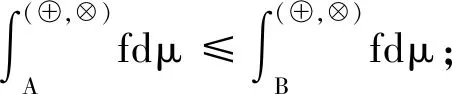
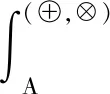
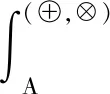
證明：(1)參見文獻[17]。

(2)令

An=μ({f>1/n}∩A)=0，n=1，2，3，…，

那么

由性質4.1，對每一個n=1，2，…，可得

即

由泛乘法的公理性質(參見文獻[17])可得μ(An)=0，n=1，2，3，…。因為μ是零連續的，所以μ({f>0}∩A)=0，即f在A上幾乎處處為零。

定理證畢。

作為定理4.1的特例，我們即可得到文獻[13][16]中的結果：

推論4.2[17]若μ是下連續的，則

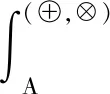
定理4.1表明在模糊測度是零連續的假定下，

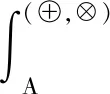
5 Choquet積分的唯一性

Choquet積分是一類重要的非線性積分，它的定義如下(見文獻[4][14][17])：

其中右邊的積分是關于α的黎曼積分，α∈[0，∞)。

Choquet積分有以下基本性質(可參見文獻[15][17]).

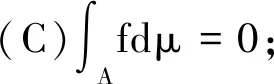
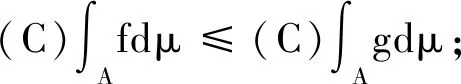
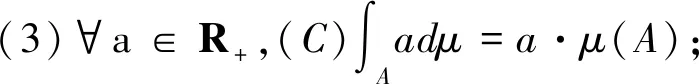
對于Choquet積分也有與泛積分類似的結果。

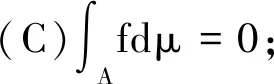
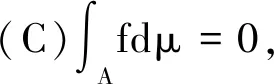
證明：(1)見文獻[15][17]。

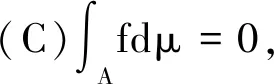
由假設μ是零連續的，從而μ({x：f(x)>0}∩A=0。即得f=0 a.e.于A.

定理證畢。

作為定理5.1的特例，我們即可得到文獻[17]中的結果：

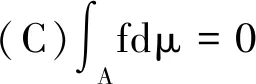
由定理4.1和5.1可得以下結果：

(1)f在A上幾乎處處等于零，即f=0 a.e.于A；

最后我們利用可測函數的收斂性刻畫單調測度的零連續性，給出零連續性的幾個等價條件。

定理5.2設(X，A，μ)是一個單調測度空間，以下幾個條件等價：

(1)μ是零連續的；

證明：我們僅證(1)?(2)，其余可類似證明。

(2)?(1)：任取{An}?A，An↗A，且μ(An)=0，n=1，2，...。令fn=XAn，f=XA(XAn，XA分別表示An和A的特征函數)，那么fn=0 a.e.且fn↗f，由條件(2)有f=0 a.e.，即XA=0 a.e.，亦即μ(A)=0。

證畢。

6 結論

本論文中，我們討論了模糊測度的零連續性，正象我們已經看到的，模糊測度的零連續性是比下連續性更弱的一個條件。在零連續的條件下我們證明了勒貝格積分的唯一性對于一般的泛積分和Choquet積分仍然成立(定理4.1和5.1)。這樣，作為泛積分特例的Sugeno積分和Shilkret積分也有相同的結果。因此，人們先前得到的相關結果(參見文獻[17])得到了進一步推廣。最后，我們揭示了模糊測度的零連續性和可測函數的收斂性之間有緊密聯系(定理5.2)。

再進一步的研究中，我們將問題的討論集中到凹積分[7]的情形，考察凹積分的相關性質。