探析數學建模思想在高等數學教學中的應用

趙青波

（三門峽職業技術學院，河南 三門峽 472000）

數學建模思想主要是通過對代數、函數等數學題目依據其內在發展規律，在腦中形成所學數學知識的相關模型，根據具體的數學題目套用其模型，在理解題目條件的基礎上將數學模型運用到解答當中，進而幫助學生更好地理清思緒、整理思路，進一步掌握數學知識的實際應用。

一、數學建模思想

數學建模包括模型準備、模型假設、模型建立、模型求解、模型分析、模型檢驗、模型應用幾個過程。數學建模是數學知識和實際生活的必要聯系，通過數學建模可將高等數學知識的抽象性特點融入現實生活，也可以把數學問題和現實問題相結合，利用數學知識解決實際問題。數學建模本身是通過模型的建立將復雜的問題轉化為簡單的數學求解，通過掌握復雜問題的規律和內涵，抓住問題的關鍵。

在建立實際問題的數量關系和數學結構中，利用直觀的數學公式來解決問題，其數學知識解決問題的過程就是數學建模思想的體現。數學建模思想具有較高的實用價值，包含了創新、應用、實踐、轉化和模型化的特點。在創新方面，利用數學建模在解決問題的時候對解題思路進行創新，對解題結果、問題應用等進行全面分析，需要學生具備扎實的數學基礎知識[1]。在應用方面，能夠將學到的數學知識、解題方法用于解決數學問題，即“學以致用”。在實踐方面，將數學理論知識和實踐聯系起來是實踐意識的體現，數學建模思想將理論性知識和實踐意識結合起來，強化、論證數學知識的實用性，激發學生對學習數學知識的興趣。在轉化方面，轉化意識是數學建模思想的重要組成部分，也是將實際問題轉化為數學問題的關鍵。通過數學問題、建模、實際問題的結合，將生活性語言轉化為數學問題，將復雜的問題簡單化，簡單的問題圖像化。在模型化方面，從實際問題復雜的條件里過濾出有用的條件，通過建立模型求解，得出具有普遍性意義的結論。

二、在高等數學教學中融入數學建模思想

（一）數學建模思想對于高等數學的促進作用

高校高等數學的教學不僅要讓學生掌握復雜的數學概念、公式和研究結論，還要在教學環節中融入對數學知識學習方法的教學，讓學生認識到高等數學的魅力，進而了解數學知識的發展和學生對于數學知識、數學文化的掌握程度[2]。高等數學的教學既要做到對實用性知識的教學，又要注重提升學生的創新意識、應用意識、轉化意識和應用能力，對高等數學進行開放性的教學，切忌固步自封。學生在開放性的高等數學教學環節中有計劃地開展對知識的學習，體現了數學知識對學生今后發展起到的促進作用。

將數學建模案例融入到高校的高等數學教學中是高校高等數學未來的發展方向之一。在高等數學教學中積極融入數學建模思想能切實提高其教學效率。師生通過對高等數學建模思想的學習可以減輕實際工作與學習中的負擔，學生在數學建模思想的影響下更容易理解高等數學的知識內容，有效避免了只對定義和概念這些硬性理論教學的枯燥感。通過融入數學建模思想，讓學生對高等數學有一個結構性的認識，能夠從被動性學習轉化為自主性學習，充分激發學生學習的積極性，進而提高學生的學習效率。

（二）在高等數學教學中融入數學建模思想的原則

1.分清主次

在高等數學教學中融入數學建模思想的原則之一就是要分清主次，對高等數學中的基礎性理論知識和實際應用的關系要處理好。高等數學課程是為理工科學生學習專業性知識提供的技術性數學工具。因此，對高等數學的教學要確保數學建模思想在高等數學教學當中的升華。以理論知識為基礎，實際應用為目的，通過數學建模思想的支持完成對基礎性知識的創新和拓展[3]。

2.靈活應用

靈活應用要求數學建模思想的融入和應用不能死搬硬套，將建模思想和高等數學教學內容有機結合起來，將數學體系與不同的數學建模聯系起來，加強高等數學知識的實用性。在高等數學教學中融入數學建模思想不能一味地追求整體性的體系建立，要避免篇幅冗長。高等數學教材的內容方面并不是越多越好，而是通過科學的知識體系，使學生能夠合理安排自己的時間，靈活地使用數學建模思想解決問題。

3.循序漸進

循序漸進是在高等數學教學中融入數學建模思想的重要原則之一。在高等數學教學中融入數學建模思想要使用恰當的方法將兩者融合[4]。在初期的高等數學教學中融入數學建模思想要盡量涉及簡單的問題，對一些簡單、直觀的高等數學知識點進行講解之后，可以在學生理解的基礎上教給其數學建模思想。學生在剛接觸數學建模思想的時候，需要以自身已經掌握的數學知識為基礎，驗證數學建模思想的實用性和可行性，進而認識到建模思想的優勢。隨后，在數學知識的選擇上逐步從簡單向困難及復雜的知識轉變，由淺及深適當地融入數學建模思想，讓學生在潛移默化中掌握對數學建模思想的應用。

4.因材施教

因材施教是我國教育事業廣泛應用的教育原則，在高等數學的教學工作中同樣適用。實際的教學工作中，不同的學生具有不同特點，學生之間的差異性導致千篇一律的數學建模案例并不能滿足不同學生學習高等數學知識的需求。因此，在教學工作當中要因材施教，開展學生差異化的現代化高等數學教學。其中，注重對貼合學生生活和學習的數學建模思想案例的收集，以和學生專業密切相關的數學建模思想案例引起學生的關注，激發學生對高等數學知識的學習興趣[5]。

5.有針對性地進行教學

有針對性地開展教學工作能夠充分發揮數學建模思想的資源性價值。針對高等數學課程的核心內容和重要公式進行重點講解，注重對建模思想的引入，將創新意識和核心概念、理論相結合，倡導學生從不同的角度思考問題，進而強化對學生創新性思維能力的培養，讓其針對實際問題和數學問題能夠提出自身獨特的見解，培養具有主觀思想能力的優秀學生群體。

6.簡明扼要

簡明扼要也是在高等數學教學中融入數學建模思想的重要原則之一。高校高等數學的教學中對基礎性概念、定義、公式講解之后，直奔主題，將數學建模思想講解給學生。讓學生明白教師在教學當中融入數學建模思想的實際用途，進而能夠將數學建模思想運用到知識的解答環境中。在教學時，教師對實際背景和應用領域內容也要進行簡單清楚地表述，使學生在問題的分析上向利用數學建模思想解題方面靠攏，不在一些

不必要的條件、細節上浪費時間。

三、在高等數學教學中融入數學建模思想的教學案例

在高等數學教學中融入數學建模思想對負責教學的教師專業性能力和素質提出了較高的要求，要求教師具備寬廣的知識面，能夠將兩者有機地結合在一起，讓學生在采用數學建模思想解決問題的過程中能夠認同高等數學的應用特點。

（一）案例分析

有一動點，要過河運動到位置O，其方向沿O目標不變，求該動點的游動曲線。

對該問題的解答可以將其轉化成數學問題，以數學建模思想結合高等數學的知識進行解題。

對模型進行假設：

1）將河流兩岸模型化，示意為平行線，河寬h；

2）動點游動速度b，河水流動速度a，且a，b為常數

3） 動點初始位置以A表示

4） 動點游動方向以O不變。

具體模型建立如圖1 所示，以O 點為坐標點，將河岸以x 軸平行方向為順水方向，y 軸為河對岸示意。

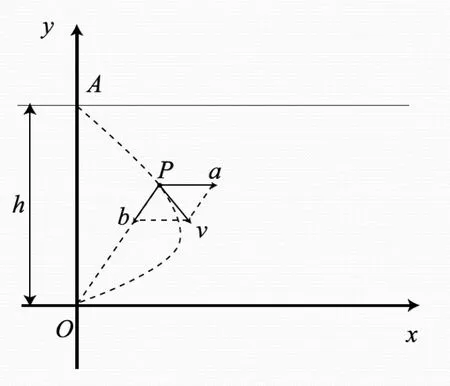
由圖1所示，題目“求該動點的游動曲線”是求互P 點坐標對于時刻（t）的表達式即可。此題可以看出，動點游動軌跡受河流流速影響，為一條平滑的曲線。通過數學建模之后，學生將題目中有用的信息提煉出來，將其轉化為微分方程計算，進而將復雜的題目簡單化，以高等數學的相關理論知識進行解題：

T時刻動點速度為：

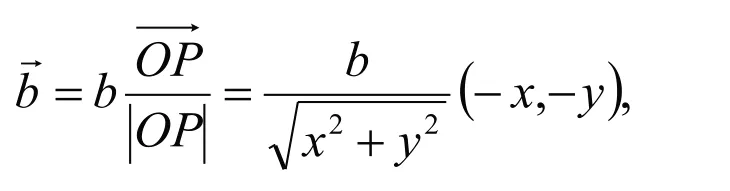
計算河流流速為 ，由此可求出動點的整體速度為

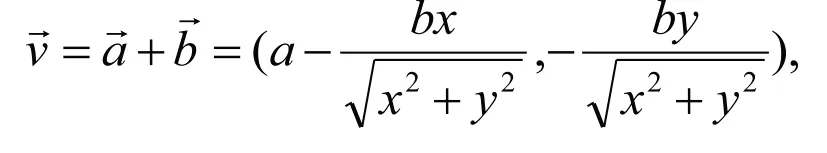
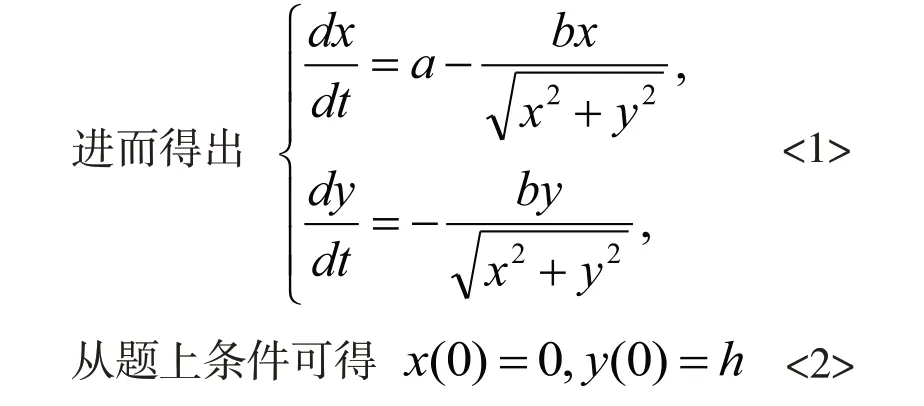
通過<1>和<2>解微分方程進而獲取最終答案。

（二）代表性案例當中數學建模思想的融入

在高校的高等數學教學中，在知識概念的學習當中融入相應的經典案例能加深學生的印象，能幫助學生在實際的問題教學中提煉問題的有用信息。比如，在對函數極限學習過后，高等數學教材的聯系關系中提出了“存款的問題”，要求學生用函數極限的知識內容解答問題。學生利用數學建模的學習方式，將存款問題轉化為具體的函數極限運算問題，將復雜的問題簡單化，加深學生對習題的理解程度。

例如：某機構在郵局購進報紙以進行零售，其進價0.5元，售價1元，在結束工作后可將為賣出報紙以0.2 元價格退回，分析如何安排購進數量，以確保實際利潤最大。

對該案例的分析和解決上要考慮到市場的變化，將市場的實際需求量概率融入到題目當中，進而以數學建模思想對題目進行分析：

設每天購進n份報紙滿足需求，此時平均收入為G，設報紙市場需求量為r的概率f（r），以循序漸進的思想考慮問題。

由題上條件可得：

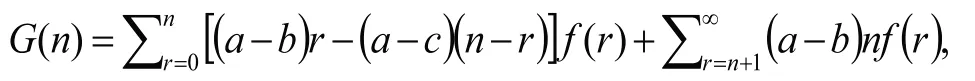
（式中“a”為報紙購進價格、b 為實際售出價，c為退回價格、r為市場實際需求，n為購進報紙數量。）此問題主要在于將實際中的經濟利益問題以數學建模思想轉化為數學問題，假設a、b、c量為已知，建立f（r）和G（n）的相應方程，將f（r）方程轉化為P（r）的概率密度函數：

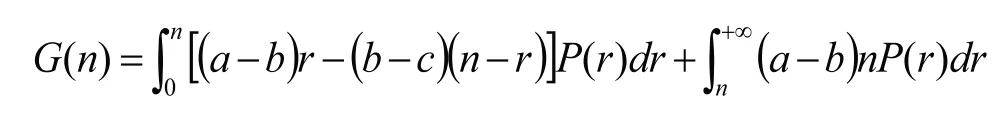
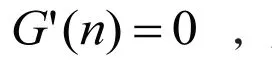
將從而得到：

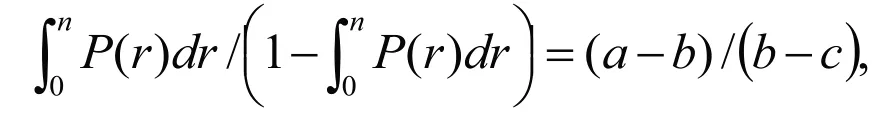
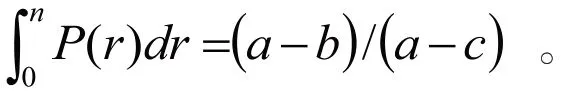
要求收入最大時，n必須滿足此題中n 在賣完和未賣完中概率比P1/P2=賣出一份和退回一份（a-b）/（b-c）。建模設需求量的服從均值500 分方差50 份正態分布，得出a-b=0.5，a-c=0.3，P1/P2=5/3， 。通過查閱對應表格得到。總體上來算，當每天購進516 份報紙時，其可獲取最大的收入G，約為23.48。

在此案例的分析中，通過運用數學建模思想，鍛煉學生的實際創新能力，以貼近生活的經濟類案例，激發學生對學習高等數學的興趣。

四、結束語

綜上所述，通過在高等數學教學中融入數學建模思想，將貼近生活的案例融入教學，引導學生采用數學建模的方式來解決貼近生活的案例問題，促進教學相長，進而切實提高高等數學教學的效率和質量。