基于模式識別欣賞“知二得一”之美

陸萬龍 何風強

【摘要】問題，是數學精神、思想、方法的重要載體，也是數學定義、定理、法則公式的具體體現，因此解題是初中數學教學中最基本的活動形式。正如G·波利亞所說：“掌握數學就是意味著善于解題。”

【關鍵詞】模式識別；知二得一；解題

本文從數學解題中的一道基本問題進行模式構建，即角平分線、平行線與等腰三角形之間的“知二得一”問題，結合三者關系構建模式，再結合典型例題研究模式識別和模式應用。所謂模式識別，就是當主體接觸到數學問題后，首先要辨別題目的類型和所給條件，再結合已有知識和經驗，將問題分解歸類，從而產生摩擦，最終能達到生成新問題的解決方法。

一、由發現“知二得一”，到一種模式的構建

在這一問題中，顯然根據平行線和角平分線來得到幾組角之間的相等關系，最后再根據“等角對等邊”轉化為邊之間的相等關系以及反過來根據“等邊對等角”來解決問題。

這樣，我們根據基本圖形，由（1）引導問題，對圖形加以分析，進而通過（2）（3）（4）三個小題使學生融會貫通，心領神會，產生遐想，再比較寫出的基本過程，發現通過等量代換來得出新的一組相等角這一基本思路，從而解決問題，最后回歸到整個問題，得到的基本結論就是最終實現三者之間的相互轉化問題，即發現三者之間的“知二得一”。

然而，我們發現這種“知二得一”的問題在數學中還有很多，以上這個問題值得再進一步去挖掘。于是，我們將“知二得一”這種解題思路形成一種模式，在數學解題中是一種值得借鑒并運用的模式。

二、從模式的構建，再到模式的識別

通過此問題，學生能很好地鍛煉邏輯思維，學會去分析問題，最后又能回歸到“知二得一”的模式上來，有效而快速地解決問題，提升解題能力。

從上述幾道問題的模式識別來看，足見一種模式的構建固然重要，但模式的識別尤為重要，這是能否解決問題的關鍵與核心。認知心理學家西蒙說：“人們在解決數學問題時，大多數是通過模式識別來解決的。首先要識別眼前的問題屬于哪一類，然后以此為引索在記憶存儲中提取相應的知識，這就是模式識別。”因此，學習一種模式，應該建立在引導學生理解這種模式基礎之上，更應該細致地教會學生如何去識別這種模式，簡單來說，就是使學生能說出此問題滿足哪種模式，如何才能解題，讓學生能心領神會地對待數學問題，最終提升解題能力，實現簡化解題與優化解題。

三、從模式的識別，最后到模式的應用

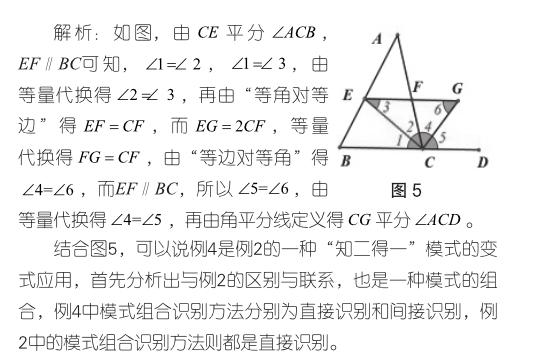
學生在掌握例2的基礎上，再結合例4可以鞏固提升，加以強化，更能體會變式訓練的趣味性，增強學習自信心，提升分析問題和解決問題的能力。

如實說，模式只是提供了一種相對穩定的樣本，既非萬能又非一成不變。當遇到一個新的、更深刻或非常規的問題時，我們需要轉化或者分解問題，還需要對模式加以重組，創造出更多或這更高層次的模式，逐漸進入得心應手的境界。

所以，在用“模式識別”來解決問題時，不僅要注意外形的分析，而且應該對題目的結構進行分析，還要注意內容上的理解，能夠從孤立靜止的數學形式中找出關聯活動的數學內容。在解題過程中，不僅要注意方法、技巧和已有數學結論的應用，而且要揭示數學內容上的轉化，注意從內容的聯系尋找解題思路。平時在數學解題中，教師要多引導學生觀察、發現、思考、歸納、應用，發現問題、提出問題、分析問題和解決問題，結合變式訓練，建立一個數學模型——解題模式，增強學生對數學基本思想的理解，加強學生對基本活動經驗的積累，最終提升學生的解題能力，這一“悟”的過程，就是對數學之美的欣賞過程。

【參考文獻】

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版） [M].北京：北京師范大學出版社，2012.

[2] 羅增儒.數學解題學引論 [M].西安：陜西師范大學出版社，2016.

[3] 劉志昂.利用變式練習，促進習題教學 [J].中學數學教學參考（中旬），2011（04）：51，64.