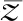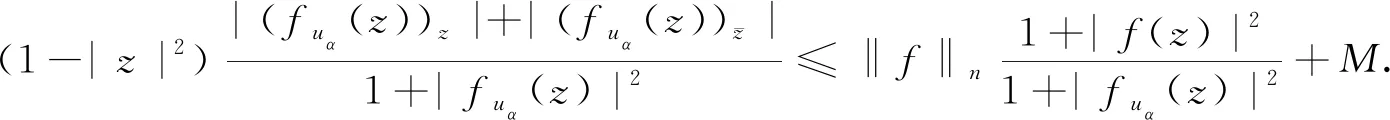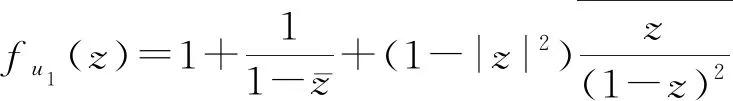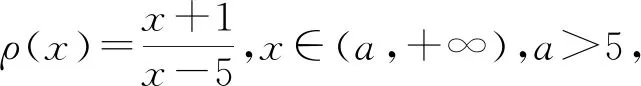調和映照的正規性

孫乾乾， 陳行堤， 胡春英

(華僑大學 數學科學學院， 福建 泉州 362021)

1 預備知識

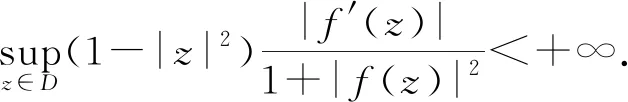
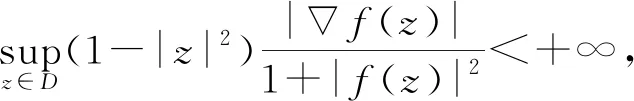
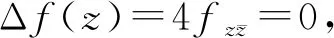
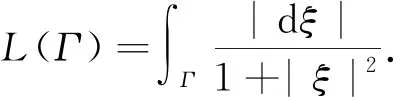
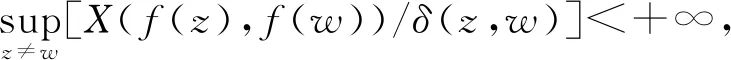
Arbelaez等[3]給出正規調和映照的一個判別定理.

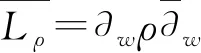
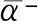
其中,Ik的遞推公式為

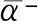
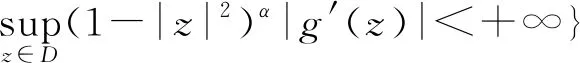
設z1，z2是區域Ω內的任意兩點，記l(γ)為連接z1，z2的任意可求長曲線的長度.若存在常數1≤M<+∞，使得l(γ)≤M|z1-z2|，則稱Ω為M-線性連結區域[11].

2 主要結論與證明

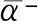
則fuα(z)是正規的.

證明: 假設‖fuα‖n<+∞，?z，w∈D，γ:[0，1]→D是連結z，w的雙曲測地線，則有

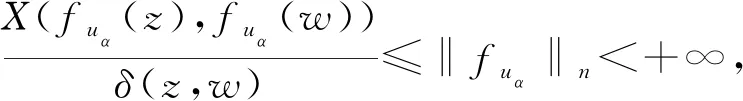
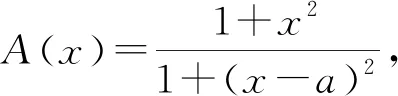
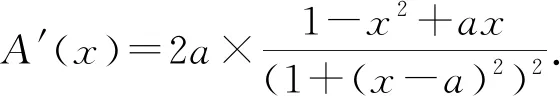
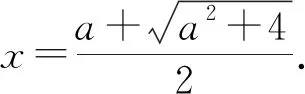
因此，A(x)在[0，+∞)內有上界.

證明：假設f(z)是正規的.由定理A得

又由定理B得

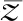
從而有

因為g(z)∈B1，所以有

所以有如下兩種情況.

1) 當|f(z)|

2) 當|f(z)|≥B1時，由引理1可得

所以有

故fu1(z)是正規的.

由g(z)∈B1當且僅當g′(z)∈B2，利用遞推知g(α)(z)∈Bα+1.從而由命題1可得到如下定理.

證明：當α=1時，命題1已證.

所以有

當n=1時，由于有g(z)∈B1，所以有

結論成立.

從而存在常數Nk+1，使得

下面給出一個具體的例子.

證明：簡單計算可知f(z)是正規的，且g(z)∈B1.又因為

所以fu1(z)是正規的.

但是當f(z)和fu1(z)是都是正規的時，g(z)不一定屬于B1.下面給出反例.

證明：因為有

所以f(z)是正規的.

所以有

故fu1(z)是正規的.

當z取實數并趨于1時有

所以g(z)?B1.

反例2說明g(z)∈B1不是必要的.

由g(z)單葉解析，有

從而有

因此，fu1(z)是正規的.