橢圓界面問題的高階差分格式
吳龍淵, 翟術(shù)英
(華僑大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 福建 泉州 362021)
1 預(yù)備知識
橢圓界面問題是一類在流體動力學(xué)、分子生物學(xué)[1]、電磁學(xué)和材料科學(xué)中廣泛存在的問題.考慮如下橢圓界面問題,即
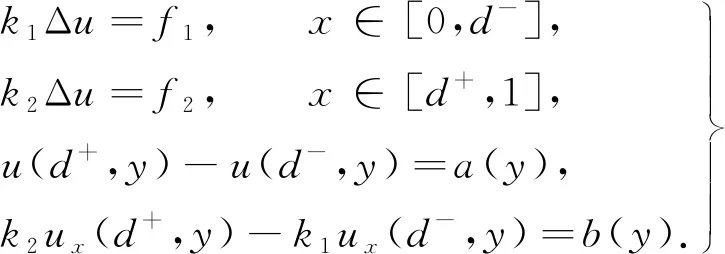
(1)
式(1)中:(x,y)∈[0,1]2,界面區(qū)域Γ={(x,y)|x=d,y∈[0,1]},邊界條件為
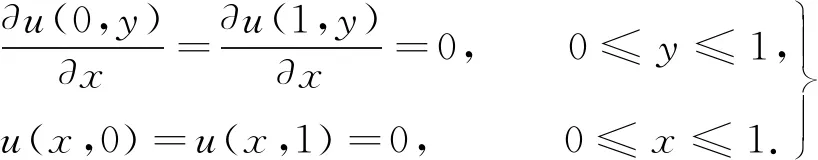
(2)
顯然,問題(1)的解在界面區(qū)域Γ上是不光滑的,甚至是不連續(xù)的.傳統(tǒng)的數(shù)值方法已經(jīng)不適用于橢圓界面問題.問題(1)的數(shù)值工作除了佩斯金的浸入邊界法[2-6]之外,還有很多學(xué)者進行相關(guān)研究[7-11].此外,有限元在橢圓界面問題中也得到了廣泛應(yīng)用[12-14].然而,以上方法都為二階精度.本文利用差分法構(gòu)建橢圓界面問題的一個高級數(shù)值格式.在求解區(qū)域內(nèi)部及界面處采用四階逼近,在邊界處應(yīng)用三階數(shù)值格式,最終得到一個具有四階精度的數(shù)值格式[15].
2 基本引理
首先給出兩個引理.
引理1假設(shè)g(x)∈C6[0,L],將區(qū)間[0,L]M等分得到一組點xi,i=0,1,2,…,M,則有
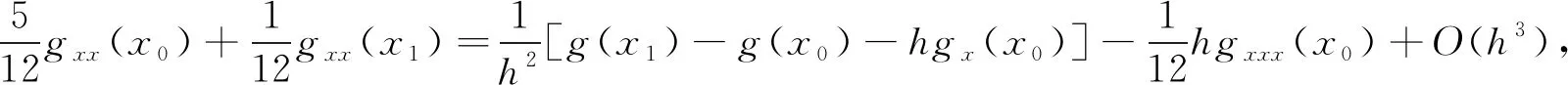
(3)

(4)
引理2[15]假設(shè)g(x)∈C6[0,L],將區(qū)間[0,L]M等分得到一組點xi,i=0,1,2,…,M.則對任意的1≤I≤M-1,有
3 數(shù)值離散
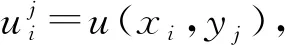
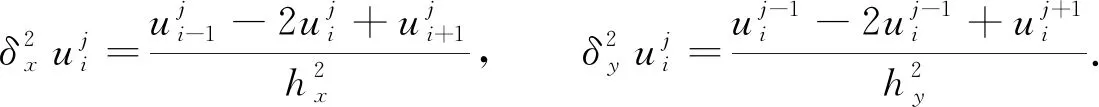
(7)
由此得到相應(yīng)四階Padé逼近[16-17],即
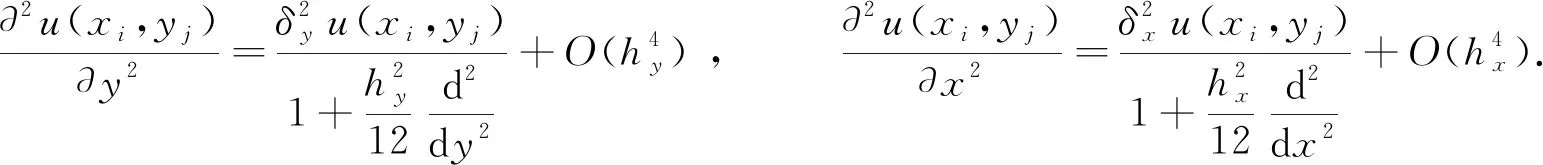
(8)
當i=1時,由引理1可知
兩邊同乘以Ly,則有
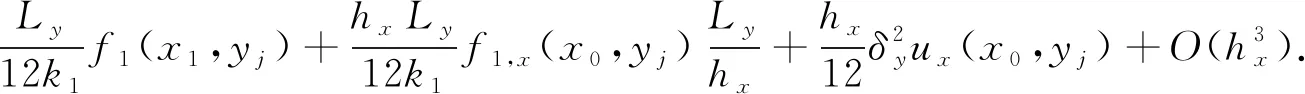
(11)
用數(shù)值解代替真解,省略誤差項,可得
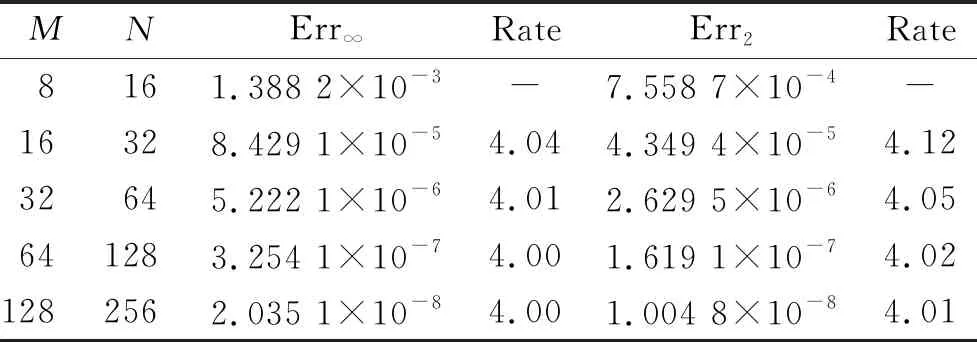
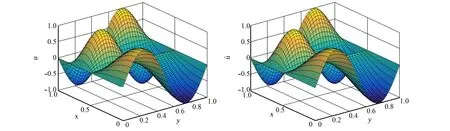
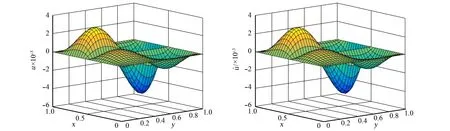
當1 (13) 特別的,當i=m時,根據(jù)式(13)可得 (14) 當i=I-時,根據(jù)引理2有 經(jīng)整理可得 當i=I+時,利用引理2有 通過將式(21)和式(18)相加,可得 由問題(1)的第3式可知u(d+,y)=u(d-,y)+a(y),將其和問題(1)的第4式代入式(22)中,可得 當I- (25) 當i=M時,由引理1可知 兩邊同乘以Ly,則有 (28) 用數(shù)值解代替精確解并省略誤差項,可得到 整理得到的格式 (30) 為驗證收斂階,選取問題 (31) 其邊界條件及初值為 其中,真解為u1(x,y)=cos(πx)sin(2πy),u2(x,y)=cos(3πx)sin(2πy). 表1 算例1的空間收斂階Tab.1 Space convergence order of example 1 (a) 數(shù)值解 (b) 真解 圖1 算例1的數(shù)值圖像(M=32,N=64)Fig.1 Numerical image of example 1 (M=32, N=64) 首先驗證收斂階,x,y方向剖分M,N同時擴大2倍,計算得到表1.從表1可知:隨著網(wǎng)格剖分變細,格式的誤差越來越小,收斂率也近預(yù)期的四階精度.這說明方法是可行的.圖1為算例1的數(shù)值圖像.從圖1可知:格式(30)可以很好地逼近真解. 為證明格式的一般性,選取如下問題 (32) 表2 算例2的空間收斂階Tab.2 Space convergence order of example 2 u1(x,y)=x2(x-1)(x-1/2)×y(y-1)(y-1/2)·exp(x+y),u2(x,y)=(x-1)2(2-x)(x-1/2)y(y-1)(y-1/2)·exp(x+y). 首先,驗證收斂階,x,y方向剖分M,N同時擴大2倍,計算得到表2.從表2可知:隨著網(wǎng)格剖分變細,收斂率也近預(yù)期的四階精度.這可說明k1和k2的取值不影響格式的有效性.圖2為算例2的數(shù)值圖像.從圖2可知:當u屬于一個很小的量級時,文中的格式依然有效. (a) 數(shù)值解 (b) 真解 圖2 算例2的數(shù)值圖像(M=32,N=32)Fig.2 Numerical image of example 2 (M=32, N=32) 提出求解橢圓界面問題的一個高階數(shù)值格式.數(shù)值實驗驗證了格式的有效性,并證明當u很小時的格式依然有效.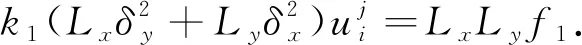
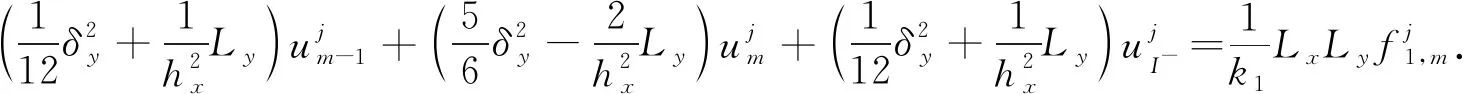
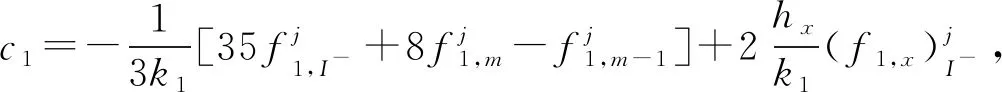
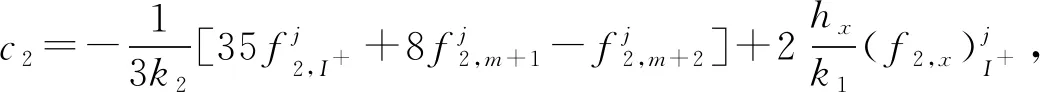
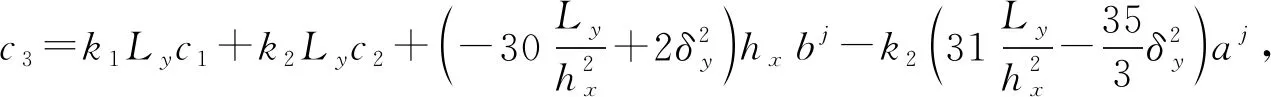
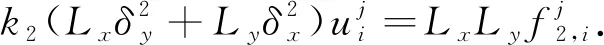
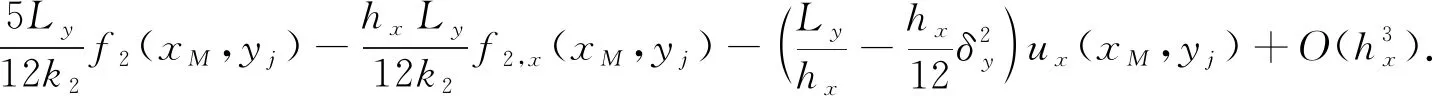
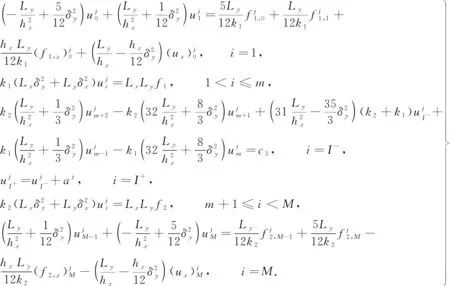
4 數(shù)值算例
4.1 算例1
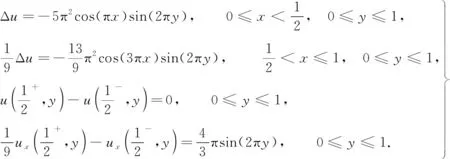
4.2 算例2
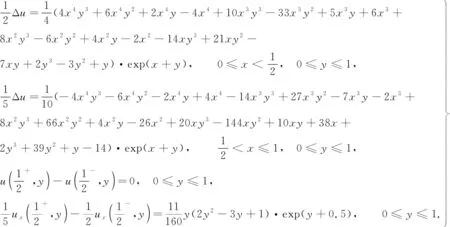
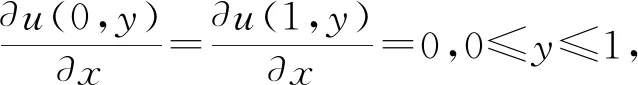

5 結(jié)束語

