基于狀態不確定性的動態濾波算法
(中南大學 數學與統計學院,長沙,410083)
1 引言
在大地測量數據中經常存在不確定性,它們影響著參數估計的準確性.不確定性是廣義的誤差,它包含可度量和不可度量的誤差[1-3].測量數據的不確定性可以是具體數值,也可能它們僅在一定的實數區間內變動,又或許是個模糊數.利用先驗信息來抑制不確定性是不確定性觀測數據平差的有效方法.在實際處理中可根據先驗信息建立對參數的約束條件[4-7],即狀態參數的不確定性.
近年來,針對狀態約束的動態問題已經有了許多深入的研究,主要的方法有:水平滑動估計法[8-10]、平滑約束卡爾曼濾波[11]、二階泰勒級數展開非線性約束濾波[12]等.文獻[13,14]將不等式約束模型轉化為規劃問題求解,文獻[15]提出了內點法,將約束問題轉換成無約束問題.文獻[16]用一系列二次規劃子問題代替原帶約束問題.文獻[17]將不等式約束轉換為橢球約束利用嶺估計計算,解是有偏的,并且不一定能滿足不等式.將不等式約束函數轉換為概率密度函數是另一種方法,但是其計算量隨著狀態維數迅速增大[18].楊元喜等引進自適應因子建立自適應抗差濾波理論[19,20],提出帶約束的抗差卡爾曼濾波模型[21].文獻[22]推導了等式約束卡爾曼濾波的解及其統計性質,指出附不等式約束和等式約束卡爾曼濾波問題的解具有相同的性質.然而上述算法并沒有有效利用已知的觀測信息,未給出顯示表達式,且計算量巨大.對于狀態約束僅考慮了等式約束和不等式約束,橢球約束的濾波模型并沒有得到討論.基于此,本文將狀態參數的不確定性定義為狀態約束,把已知的觀測信息與平差準則結合,轉化為具有約束的規劃問題,利用拉格朗日乘數法求解,推導出無約束、不等式約束和橢球約束下的濾波算法.
2 無約束濾波算法
在無狀態約束時,考慮下面的濾波模型
xk=Φk,k-1xk-1+wk,
Lk=Hkxk+vk,
其中狀態向量xk∈n,觀測向量Lk∈m,Φk,k-1是狀態轉移矩陣,Hk為m×n階系數矩陣,wk∈n和vk∈m分別為狀態噪聲和觀測噪聲向量,且滿足
Ewk=0,Evk=0,

令
(1)
(2)
對濾波模型建立平差準則
(3)

我們有
(4)
式(4)即為卡爾曼濾波模型中狀態估計的遞推公式.
現在將平差準則(3)變為如下形式

(5)
忽略與xk的無關項,平差準則(5)可寫為
(6)
其中
(7)
對式(7)求逆有
(8)
因此我們得到無約束濾波算法:
無約束濾波算法與卡爾曼濾波公式是一致的,式(8)是Pk的遞推公式,式(6)是度量測量信息L0,L1,…,Lk對狀態xk的影響.
3 不等式約束濾波算法
在平差測量中狀態參數的不確定性可表示為區間約束(如某些狀態參數大于零),因此有不等式約束模型
xk=Φk,k-1xk-1+wk,
Lk=Hkxk+vk,
Gkxk≤qk.
相應的不等式約束下的平差準則最優化問題為
(9)
s.t.Gkxk≤qk.
為求解此最優化問題,構造廣義Lagrange函數
(10)


G1kxk=q1k,
和
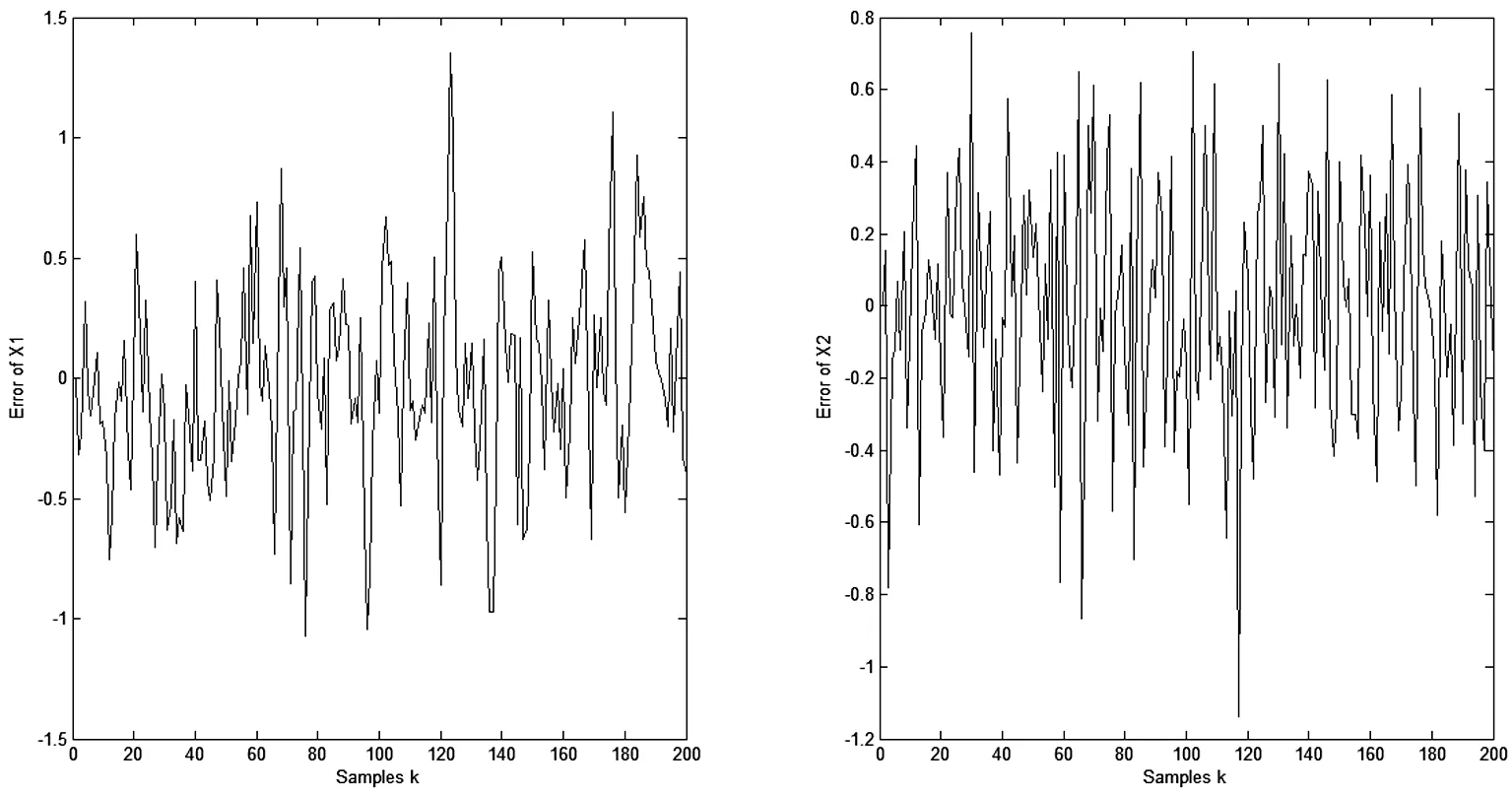
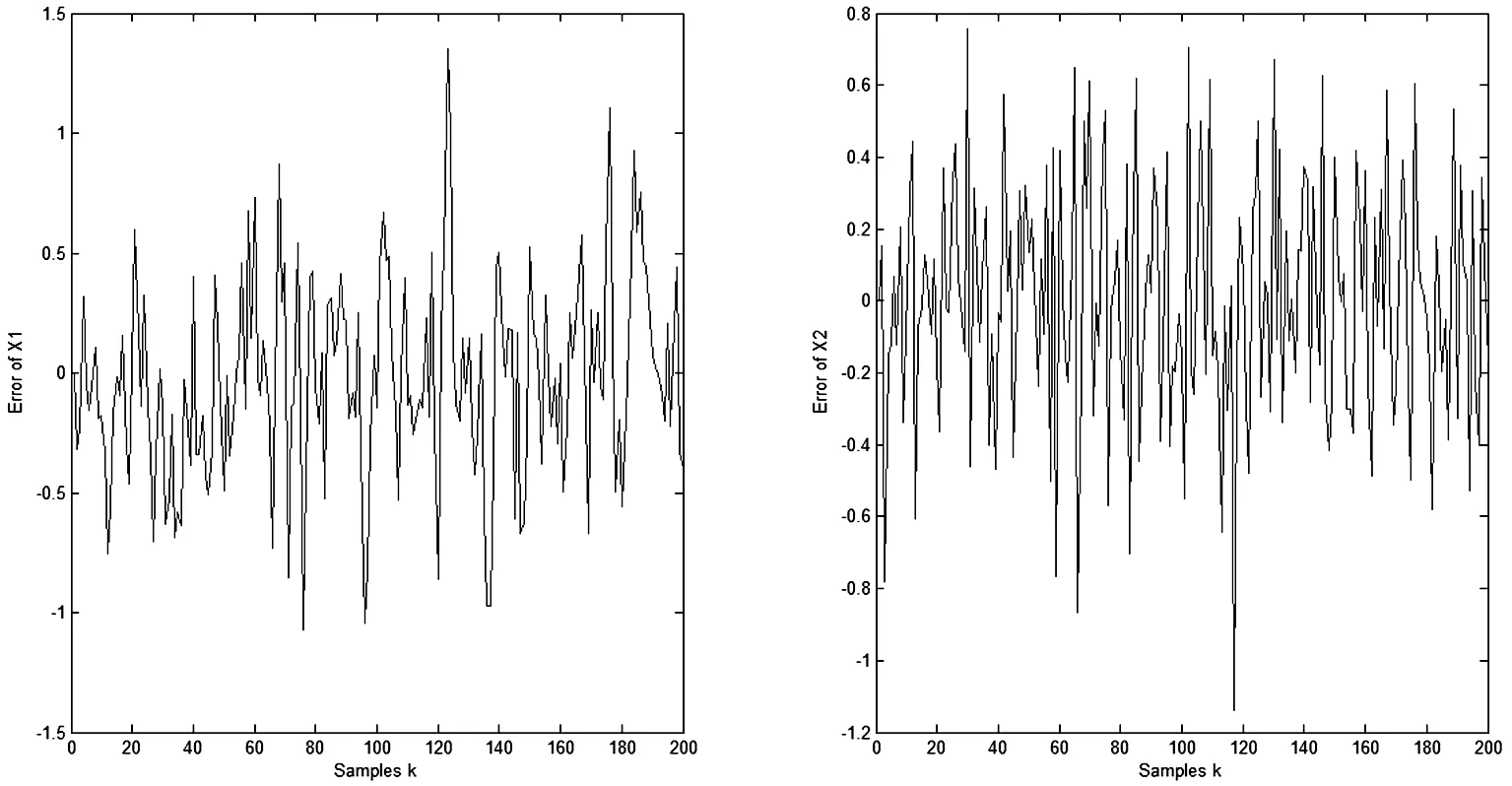
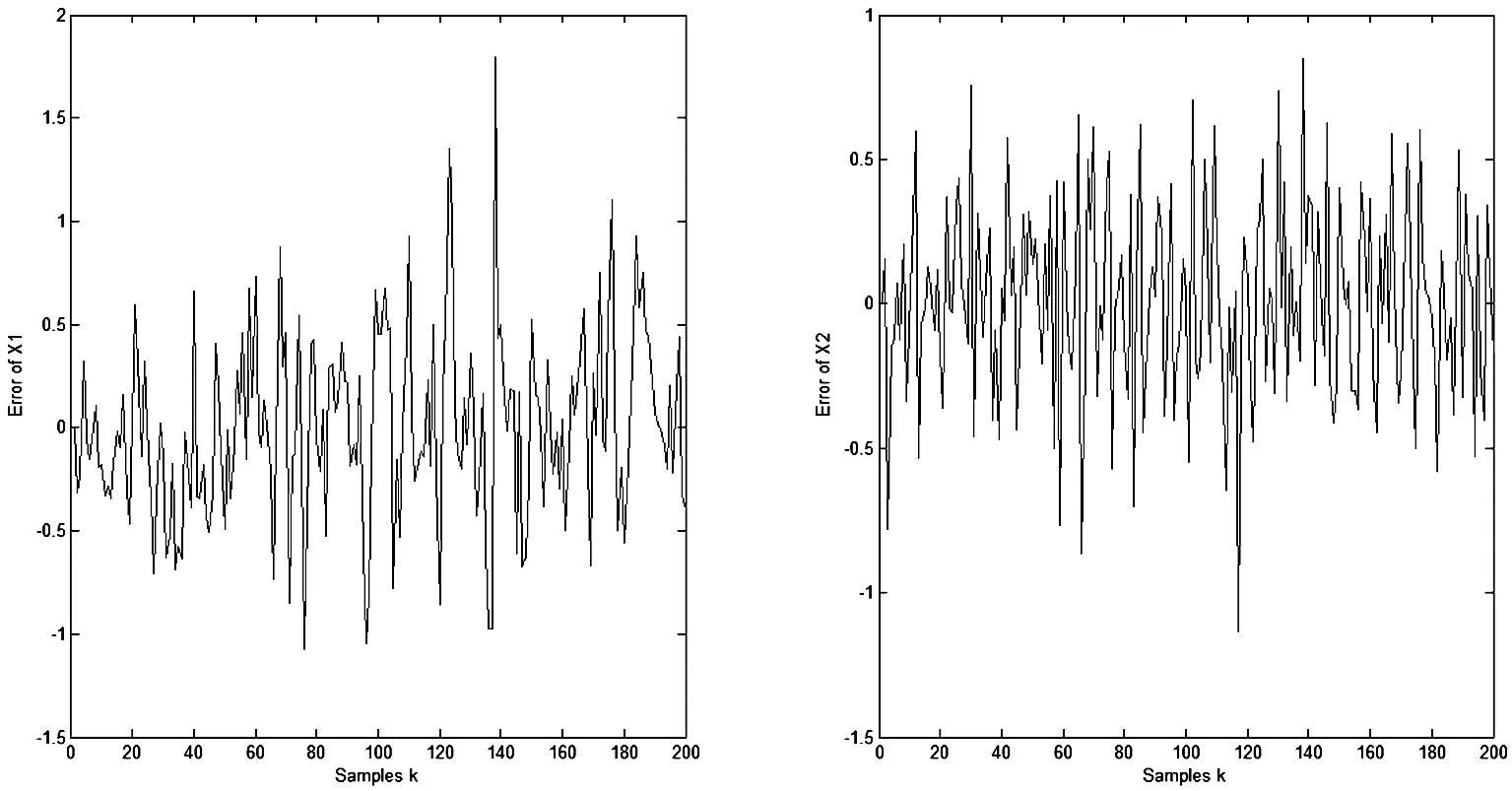
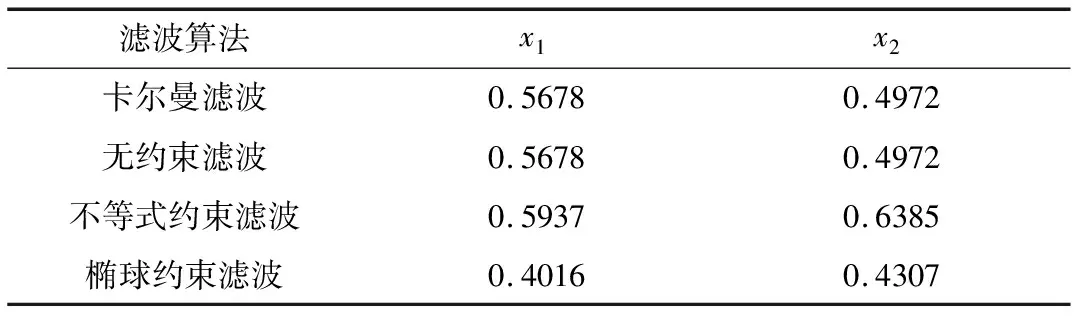
G2kxk 令 (11) 則有 (12) (13) 由(11)和(12)式,并忽略式(12)中與xk無關的項,得到如下的平差準則 (14) 式中 (15) 因此不等式約束濾波算法為: 式(12)是不等式約束濾波解的遞推估計方程,式(15)是Pk的遞推公式,式(14)是度量測量信息L0,L1,…,Lk對狀態xk的影響. 濾波模型中狀態參數存在橢球約束的濾波模型可表示為 因此橢球約束下的最優化問題為 (16) s.t.Lk=Hkxk+vk, 為求解此問題,構造廣義Lagrange函數 (17) 式中μk≥0.求解式(17)可得 (18) (19) (20) 其中 (21) 平差準則(21)經過適當變形,并忽略與xk無關的項可表示為 (22) 其中 (23) 因此橢球約束濾波算法為: 式(20)是橢球約束濾波解的遞推估計方程,式(23)是PCE,k的遞推公式,式(22)是度量測量信息L0,L1,…,Lk對狀態xk的影響. 為了檢驗算法的有效性和性能,考慮下面的二元狀態變量的濾波模型 圖1 標準卡爾曼濾波算法的誤差 從圖1、圖2看出,無約束濾波算法與標準卡爾曼濾波算法中的x1和x2的誤差值并無差別.圖3和圖4表明,當考慮狀態參數不等式約束和橢球約束的不確定性時,本文提出的不等式約束濾波算法和橢球約束濾波算法能有效地利用這一先驗信息對狀態進行估計.整體來看不等式約束濾波算法的估計誤差略大于無約束濾波算法,但整體誤差趨勢一致.而橢球約束濾波算法的估計誤差小于無約束濾波算法,估計效果最佳. 圖2 無約束濾波算法的誤差 圖3 不等式約束濾波算法的誤差 圖4 橢球約束濾波算法的誤差 為了更加清晰地比較不同濾波算法的性能,本文進行了1000次蒙特卡洛模擬實驗,結果見表1.通過比較不同濾波模型的RMS值發現:無約束濾波算法與卡爾曼濾波算法具有一致性.橢球約束濾波算法比無約束濾波算法能更準確地進行狀態估計.而不等式約束濾波算法的RMS值略高于其余三種濾波算法. 表1 不同狀態約束濾波算法的RMS比較 在實際測量中,狀態參數的不確定性不能被忽略.本文利用狀態約束這一區間形式表示狀態參數的不確定性,基于平差準則并結合狀態方程分別建立無約束、不等式約束和橢球約束濾波模型,并運用已知觀測信息,將模型化為規劃問題求解,最終推導出的無約束濾波算法、不等式約束濾波算法和橢球約束濾波算法的顯式表達式.其中無約束濾波算法與卡爾曼濾波算法具有一致性,且三種模型最終具有統一的平差準則.仿真實驗結果表明:三種模型均能準確地進行狀態估計,并且運算高效、簡便.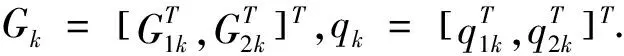

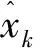
4 橢球約束濾波算法




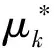
5 仿真實驗



6 結論

