Uniqueness on Recovery of the Permeability and Permittivity Distributions

Deng Youjun and Tang Wanjing

(School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China)

Abstract We consider the recovery of piecewise constants permeability and permittivity distributions in the Helmholtz system. First, the so called Calderón’s identity is extended to suit for Helmholtz system. Then we show that the uniqueness of recovery by using only one measurement under some mild condition on the measurement, which is new to the literature.

Key words Uniqueness Layer potential Transmission condition Helmholtz equation

1 Introduction

Mathematically, we consider the following Helmholtz system:

(1.1)

wherew>0 is a given frequency.Here the permeability and permittivity distributions are given by

(1.2)

Recently there are rapidly growing interests in the recoveries of the inclusion and parameter. The global uniqueness results are obtained when the domain is restricted to be convex polyhedrons and balls in three-dimensional space and polygons and disks in the plane(see [1,2,3,4,5,6]). The uniqueness on recovery of piecewise constant conductivity was obtained by one of the authors (see [7]), where it was proved that one measurement on any surface enclosing the unknown medium is sufficient for the recovery of the conductivity in a two layer structure.

There are also many results concerning the unique determination in recovering of obstacles in inverse scattering problems. In [8], a uniqueness for a two-dimensional polygon or a three-dimensional polyhedron is presented by the far-field pattern corresponding to an incident plane wave at one given wavenumber and one given incident direction. The far-field pattern for a single incident wave at a fixed frequency uniquely determine the shape and location of a convex polygonal obstacle in [9]. The authors of [10] proposed the idea of using complex exponential solutions to demonstrate uniqueness in the linearized inverse conductivity problem. The uniqueness in an inverse acoustic obstacle scattering problem for both sound-hard and sound-soft polyhedral scatterers was obtained in [11], where it is proved that a general sound-hard polyhedral scatterer inRN(N≥ 2) is uniquely determined by N far-field measurements and a general sound-soft polyhedral scatterer is uniquely determined by a single incoming wave.

In addition, it is proved in [12] that a general polyhedral perfect conducting obstacle is uniquely determined by the measurement of the far-field pattern corresponding to a single incident wave. The authors of [13] showed that if a medium is piecewise constant within two general polyhedral geometries, then one can uniquely recover it by a suitable single far-field measurement. In [14], a uniqueness result for a two-dimensional piecewise conductive medium body associated with a polygonal-nest or a polygonal-cell geometry is derived by a single far-field measurement.

The purpose of this paper is to extend the Caldron’s identity (see [7]) to corresponding identity in the Helmholtz equation and then use this corresponding identity for solving the uniqueness recovery problem, i.e., recovering the permeability and permittivity distributions.

The organization of this paper is as follows. In Section 2, we introduce the layer potential techniques for our later usage. In Section 3, we show our main unique recovery result. Conclusions are made in Section 4.

2 Layer potential formulation

Let Φk(x) be the fundamental solution forΔ+k2,that is forx≠0,

(2.1)

(2.2)

(2.3)

(2.4)

It is well known that

(2.5)

(2.6)

Let Γ(x) be the fundamental solution forΔ,that is forx≠0,

(2.7)

For a boundedC2-domainDinR3, letSDbe the single layer potential defined by Γ,that is,

(2.8)

we also define a boundary integral operatorKDonL2(?D) by

(2.9)

3 Unique recovery results

(3.1)

It can be seen that the solution to (3.1)can be represented by

(3.2)

whereφ0,φ1,φ2andψsatisfy

(3.3)

(3.4)

We first compute the adjoint of (Kl1)*. Denote by <,>L2(?B) the scalar product onL2(?B). It is easy to see that

(3.5)

and

(3.6)

(3.7)

Lemma 3.1LetE∈R3be a boundedC2-domian.

(I) Ifuis a solution ofΔu+k2u=0 inE,then

(3.8)

(II) Ifuis a solution of

(3.9)

then

(3.10)

Proof

we get the proof of (I).

this completes the proof.

Lemma 3.2

(3.11)

(3.12)

By taking the limit asx→?Efrom outsideEand using the jump relation (2.6) of the double layer potential,we obtain (3.11).

Lemma 3.3Let the operatorsSkand (Kk)*be given by

Then

Sk(Kk)*=KkSk

(3.13)

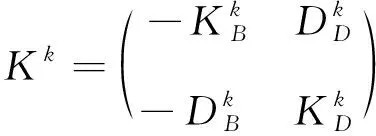
ProofNote that

We now check the following.

This implies (SkKk)*)11=(KkSk)11.

and by taking the limit asx→?B|-, we find

(3.14)

and thus we have

(3.15)

Summing up (3.1) and (3.15) we find that (Sk(Kk)*)21=(KkSk)21.

and thus we have

(3.16)

and by taking the limit asx→?D|+, we find

(3.17)

Summing up (3.16) and (3.17) we find that (Sk(Kk)*)12=(KkSk)12.

The functionsφ∈L2(?B) andψ∈L2(?D).This completes the proof.

Letujbe the solution to (1.1) with permeabilityμjand permittivity distributionεj,j=1,2, in the following form

(3.18)

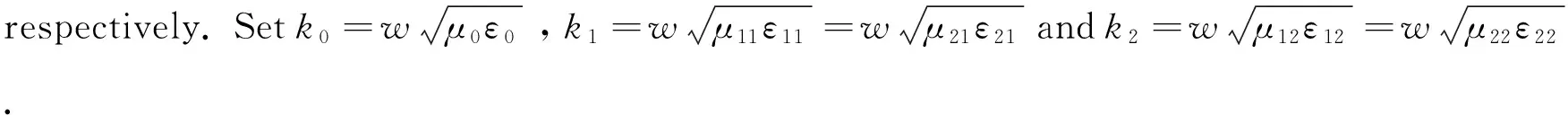
(3.19)

(3.20)

(3.21)

(3.22)

wherew1,w2andt1are defined in (3.19).

(3.23)

By applyingSk1on both sides of (3.23) and using Lemma 3.3, one thus has

(3.24)

Then

(3.25)

(3.26)

Thus (3.25) can be rewritten by

(3.27)

Next,supposeψ∈L2(?D) and defineξ1∈L2(?D) by

(3.28)

(3.29)

wherel1andζ1are given by

By taking inner product of both sides of (3.27) with (w1|?B,ψ) and using (3.29),and some straightforward calculations one then has

(3.30)

One can further decomposew1andl1by

(3.31)

and

(3.32)

respectively.Thus (3.30) can be rewritten by

(3.33)

Similarly,by consideringu2in the same way one has

(3.34)

By subtracting (3.33) from (3.34) and some elementary calculations one finally obtians

(3.35)

where

(3.36)

By using the assumption that M is invertible,one thus hasx1=x2=x3=0 and soμ1i=μ2i,ε1i=ε2i,i=1,2. The proof is complete.

4 Conclusion

In this paper, we considered a two-layer piecewise constant Helmholtz system, and showed the uniqueness on recovery of the parameters by using only one measurement, with some mild restriction on the measurement. One try treat this as special measurement in priori. One can also find out from the proof that the methods can also be used to prove the uniqueness of the piecewise constant parameters with multiple-layers, in the condition that the measurement has a specified priori information. This will be our future work in generalizing the uniqueness result to multiple-layer structure Helmholtz problem.