基于Matlab的混沌特性分析

石雨鑫

摘要：本文提出了一個(gè)新型三維連續(xù)自治混沌系統(tǒng)。通過matlab數(shù)值仿真軟件進(jìn)行仿真，繪制出了新系統(tǒng)的混沌吸引子圖、分岔圖、李雅普諾夫指數(shù)等，并分析其動(dòng)力學(xué)特性。

關(guān)鍵詞：新混沌系統(tǒng);混沌特性分析;分岔圖

中圖分類號(hào)：TP311 文獻(xiàn)標(biāo)識(shí)碼：A 文章編號(hào)：1007-9416（2020）03-0213-02

0 引言

混沌現(xiàn)象廣泛存在于各個(gè)領(lǐng)域，這使得混沌系統(tǒng)的研究具有很好的發(fā)展前景。自上世紀(jì)60年代Lorenz在研究氣候變化的實(shí)驗(yàn)中，發(fā)現(xiàn)了第一個(gè)混沌吸引子以來，新的典型混沌系統(tǒng)不斷被人們所提出，除此之外，許多新型自治混沌系統(tǒng)也陸續(xù)被發(fā)現(xiàn)。

本文提出了一個(gè)新的三維自治混沌系統(tǒng)，通過理論分析以及matlab數(shù)值仿真分析該系統(tǒng)的動(dòng)力學(xué)特性。

1 新混沌系統(tǒng)模型及其基本特性分析

1.1 新混沌系統(tǒng)模型

本文所要提出的新混沌系統(tǒng)其數(shù)學(xué)模型為：

（1）

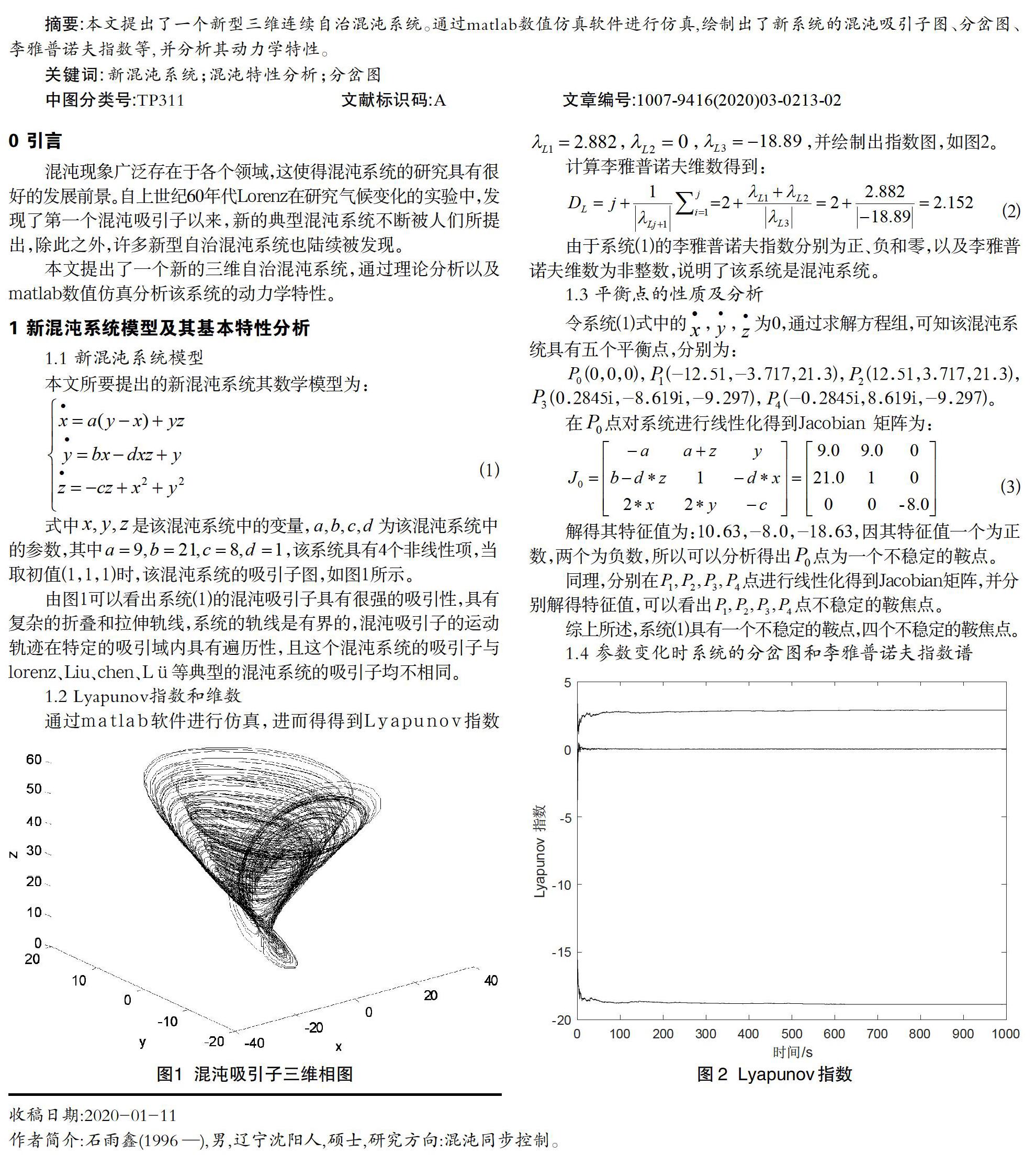
式中是該混沌系統(tǒng)中的變量，為該混沌系統(tǒng)中的參數(shù)，其中，該系統(tǒng)具有4個(gè)非線性項(xiàng)，當(dāng)取初值（1，1，1）時(shí)，該混沌系統(tǒng)的吸引子圖，如圖1所示。

由圖1可以看出系統(tǒng)（1）的混沌吸引子具有很強(qiáng)的吸引性，具有復(fù)雜的折疊和拉伸軌線，系統(tǒng)的軌線是有界的，混沌吸引子的運(yùn)動(dòng)軌跡在特定的吸引域內(nèi)具有遍歷性，且這個(gè)混沌系統(tǒng)的吸引子與lorenz、Liu、chen、Lü等典型的混沌系統(tǒng)的吸引子均不相同。

1.2 Lyapunov指數(shù)和維數(shù)

通過matlab軟件進(jìn)行仿真，進(jìn)而得得到Lyapunov指數(shù)，，，并繪制出指數(shù)圖，如圖2。

計(jì)算李雅普諾夫維數(shù)得到：

（2）

由于系統(tǒng)（1）的李雅普諾夫指數(shù)分別為正、負(fù)和零，以及李雅普諾夫維數(shù)為非整數(shù)，說明了該系統(tǒng)是混沌系統(tǒng)。

1.3 平衡點(diǎn)的性質(zhì)及分析

解得其特征值為：10.63，-8.0，-18.63，因其特征值一個(gè)為正數(shù)，兩個(gè)為負(fù)數(shù)，所以可以分析得出點(diǎn)為一個(gè)不穩(wěn)定的鞍點(diǎn)。

同理，分別在點(diǎn)進(jìn)行線性化得到Jacobian矩陣，并分別解得特征值，可以看出點(diǎn)不穩(wěn)定的鞍焦點(diǎn)。

綜上所述，系統(tǒng)（1）具有一個(gè)不穩(wěn)定的鞍點(diǎn)，四個(gè)不穩(wěn)定的鞍焦點(diǎn)。

1.4 參數(shù)變化時(shí)系統(tǒng)的分岔圖和李雅普諾夫指數(shù)譜

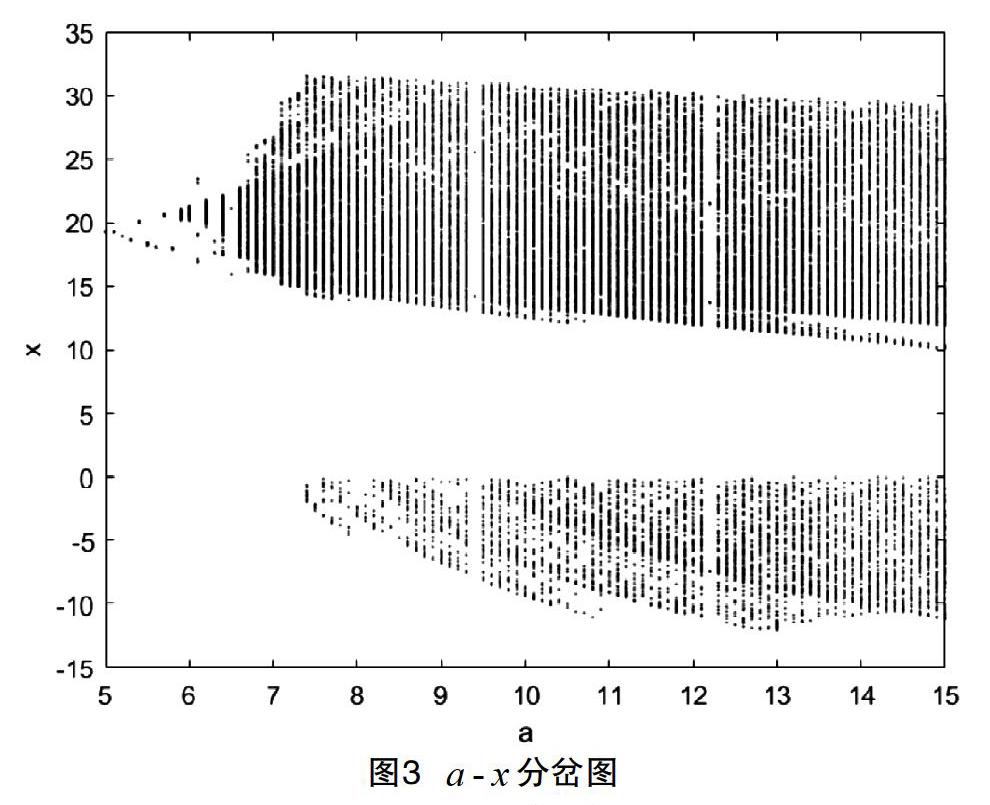
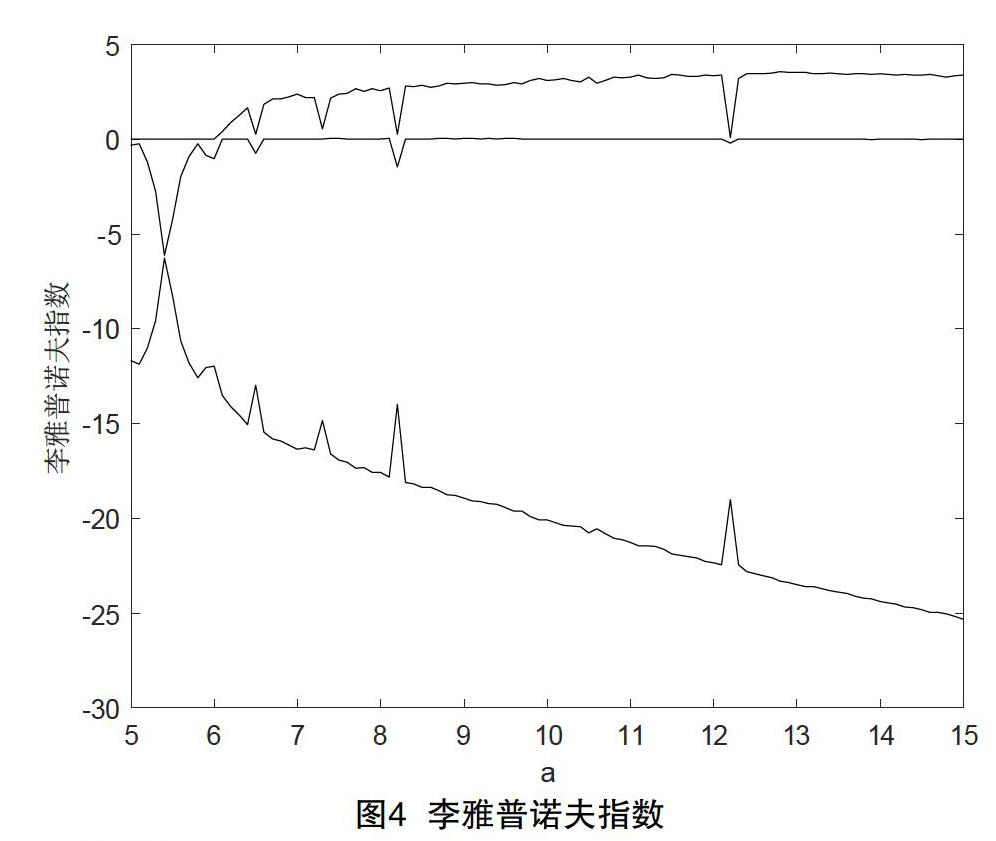
當(dāng)固定參數(shù)，，，并使，系統(tǒng)關(guān)于的分岔圖和李雅普諾夫指數(shù)譜如圖3，圖4所示。

從圖中可以看出α在區(qū)間[5，6.2）時(shí)處于周期狀態(tài)，李雅普諾夫指數(shù)均小于0。當(dāng)在區(qū)間上[6.2，15]時(shí)，最大李雅普諾夫指數(shù)大于0，系統(tǒng)由周期態(tài)進(jìn)入混沌狀態(tài)。

2 結(jié)論

本文提出了一個(gè)新的三維自治混沌系統(tǒng)并通過理論分析、數(shù)值仿真、李雅普諾夫指數(shù)和維數(shù)計(jì)算、平衡點(diǎn)的穩(wěn)定性、分岔圖和李雅普諾夫指數(shù)譜分析了新混沌系統(tǒng)的動(dòng)力學(xué)特性。

參考文獻(xiàn)

[1] Lorenz E N.Deterministic non-periodic flows[J].J Atoms Sci，1963（20）：130-141.

[2] Chen G R，Ueta T.Yet another chaotic attractor[J].Int J Bi-furc Chaos，1999，9（7）：1465-1466.

[3] Lü J H，Chen G R.A new chaotic attractor comd[J].Int J Bi-furc Chaos，2002，12（3）：659-661.

[4] 蔡國(guó)梁，譚振梅，周維懷，等.一個(gè)新的混沌系統(tǒng)的動(dòng)力學(xué)分析及混沌控制[J].物理學(xué)報(bào)，2007，56（11）：6230-6237.

Abstract：A novel 3D continuous autonomous chaotic system is proposed in this paper. By matlab numerical simulation software， the chaotic attractor， bifurcation and Lyapunov exponent of the new system are drawn and their dynamic characteristics are analyzed.

Key words：new chaotic system; chaotic characteristiec; bifurcation diagram