含板類柔性附件的充液航天器動力學研究
閆玉龍,申云峰,岳寶增
(1. 太原理工大學數學學院, 太原 030024; 2. 鄭州工業應用技術學院信息工程學院, 鄭州 451150; 3. 北京理工大學宇航學院, 北京 100081)
0 引 言
隨著現代航天事業的快速發展,航天器需要裝配柔性附件和一定數量的液體推進劑以完成復雜的航天任務。例如,為實現航天器的長期在軌運行,航天器通常安裝大型的太陽能帆板以提供必要的能量來源。因此,板類柔性附件是航天器系統的重要組成部分。航天器在軌過程中柔性附件會不可避免地產生彈性振動,對航天器的姿態和軌道造成嚴重的影響。此外,在軌航天器往往處于微重力狀態,在該種情況下表面張力對液體推進劑的動力學行為起著不可忽略的影響,毛細效應使得儲腔液體靜液面發生大幅彎曲呈現新月形[1-3]。同時,微重力環境使得液體晃動的固有頻率顯著降低,與柔性附件的振動頻率相接近,容易產生共振現象,對航天器的動力學行為造成顯著影響。因此,對含有板類柔性附件的充液航天器動力學研究具有十分重要的理論意義和工程價值。
在儲腔容積相同的情況下,球形儲腔的表面積最小,能夠有效地降低航天器的質量。眾多學者對含有球形充液儲腔航天器系統的液體晃動以及剛-液耦合動力學和控制問題進行深入研究[4-8]。由于該類曲壁軸對稱儲腔的壁面不平行于儲液腔的對稱軸,難以給出勢函數的解析表達式,因此對于該類儲腔液體晃動的解析研究是較為困難的。通過變分法和最小勢能原理,能夠獲得凸軸對稱儲液腔靜液面的控制微分方程以及穩態構形[9]。基于曲壁軸對稱儲腔的幾何特點,文獻[10]采用特殊坐標系得到凸軸對稱儲腔液體常重力下的晃動頻率,且該方法適用于任意充液深度。Utsumi[11-14]通過引入特殊的球坐標系對于凸軸對稱儲腔的液體晃動動力學進行研究,采用Gauss超幾何級數獲得晃動勢函數和液面波高的解析形式,從而得到球形儲腔中的液體在橫向和軸向激勵下的晃動頻率、波高、晃動力和力矩等晃動參數,該種方法可用于研究常重力和不同微重力環境的工況下液體晃動行為。對含有球形儲腔的充液航天器,可采用Hamilton-Ostrogradskiy變分原理推導動力學方程,得到晃動液體受到任意方向外激勵的等效力學模型[15]。對含有多個軸對稱充液儲腔的航天器,可通過復合控制方法對航天器的姿態和軌道機動控制進行研究。研究結果表明,若在設計姿態和軌道控制器時沒有充分考慮液體燃料晃動的影響,則系統將會出現剛-液-控耦合問題并導致航天器姿態不穩定[16-18]。
Kane等[19]討論了含有柔性附件剛體的平動和轉動相互耦合的情況,首次提出由于柔性附件的幾何非線性變形與剛體運動相互耦合導致的動力剛化這一概念。對由中心體和柔性附件組成的柔性航天器,可通過混合坐標法,采用準坐標形式的Lagrange方程,建立柔性航天器的混合坐標動力學方程[20]。文獻[21-23]研究由剛性平臺和若干相對于剛體發生轉動的柔性附件組成的航天器系統,采用基于準坐標下的Lagrange方程構建系統的動力學模型。通過空間離散化和截斷,將系統的偏微分方程轉換為便于進行數值仿真和計算的非線性離散狀態方程。對于中心剛體-旋轉梁的系統,梁的振動頻率和模態會隨著剛體的轉動慣量和梁的轉速而發生改變[24]。文獻[25]對附著在空間運動體上柔性懸臂梁的動力剛化問題進行系統研究,考慮梁橫向二維振動和縱向一維振動的情況,采用假設模態法對柔性梁的運動進行離散,研究橫向變形和縱向變形的耦合效應。此外,航天器柔性附件在瞬態熱效應下產生熱變形,對航天器的姿態產生擾動[26-27];在航天器編隊飛行問題中,也存在柔性航天器和剛性航天器的相對姿態動力學和主動控制問題,需要設計姿態反饋控制器實現航天器編隊飛行[28]。由此可見,航天器動力學和控制的研究中廣泛存在著剛-柔耦合動力學問題。
柔性航天器通常含有液體燃料,液體燃料的晃動與剛體運動、柔性附件振動相互耦合,會產生復雜的動力學現象和控制問題[29-30]。對于該類復雜充液柔性航天器系統,通常采用多體動力學的研究方法進行分析。文獻[31-32]將晃動液體和柔性附件分別等效為兩個質量-彈簧模型和懸臂板模型,并將重力梯度力矩作為航天器的主要擾動力矩,設計PID控制器進行航天器姿態鎮定,并對耦合情況進行分析。呂敬等[33]對帶彈性附件以及矩形貯箱的剛-液-彈耦合系統進行研究,得到外力矩作用下俯仰運動的耦合動力學模型,分析液體和彈性體對航天器主剛體運動的影響。
板類柔性附件具有較大的長寬尺寸,但是厚度較小。基于航天器板類柔性附件的幾何尺寸和材料特點,可采用薄板模型對板類柔性附件進行建模和動力學行為研究。本文采用Kirchhoff-Love薄板模型對太陽能帆板的變形進行研究,通過變分原理推導微重力環境下凸軸對稱充液儲腔的液體晃動控制方程,獲得剛-液-柔耦合航天器系統的動力學模型,研究了耦合航天器系統各部分的耦合效應,并討論柔性附件的裝配位置對耦合航天器系統動力學行為的影響,以期為航天器總體設計提供參考依據。
1 耦合航天器系統的動力學模型
考慮如圖1所示的剛-液-柔耦合航天器系統,由航天器主剛性平臺、板類柔性附件和軸對稱充液儲腔組成。在研究中做出如下基本假設:1)儲液腔的液體運動是無黏、無旋、無阻尼、不可壓縮;2)儲液腔為剛性;3)液體表面位移相對于靜平衡液面足夠小,在研究過程中可用線性化理論進行處理;4)采用Kirchhoff-Love板模型分析板類柔性附件的變形,板彎曲時中面各點只有垂直中面的位移w,沒有平行中面的位移。

圖1 剛-液-柔耦合航天器示意圖Fig.1 Diagram of rigid-liquid-flex coupled spacecraft system
1.1 柔性航天器動力學
考慮如圖1所示的耦合航天器系統。航天器剛體平臺質量為m0,為研究航天器位置和姿態運動,引入如下坐標系統:OeXeYeZe為慣性坐標系,以航天器剛性平臺的質心O為原點建立航天器本體坐標系Oxyz,其中Ox,Oy,Oz軸為慣性主軸,航天器主剛體的轉動慣量為J0=diag(J11,J22,J33)。令θ=[θx,θy,θz]T為本體坐標系相對于慣性系的Euler角。為方便起見,定義坐標變換矩陣按照Ox→Oy→Oz的順序,從慣性坐標系OeXeYeZe到本體坐標系Oxyz的轉換矩陣為
(1)
其中,sk=sinθk,ck=cosθk,k=x,y,z(下同),rOeO為O相對于原點Oe的矢徑,本體系在慣性系下的角速度為ω=[ω1,ω2,ω3]T,原點O在慣性系下的平動速度為v=[v1,v2,v3]T,則
(2)
式中:
(3)
板類柔性附件的一邊與航天器主剛體相固連,其余三邊為自由端,該類柔性附件也稱為懸臂板。板的中性面位于航天器本體系的Oxy平面。如圖2所示,點B位于板中性面的邊緣,該點在航天器本體系的矢量為rOB=[xb,yb,0]T。板沿Ox,Oy,Oz軸的長度分別為a,b,h,即板的長度、寬度和厚度,板的密度為ρ,彈性模量為E,泊松比為μ,質量為ma=ρabh。

圖2 板類柔性附件示意圖Fig.2 Diagram of plate-type appendage
考慮板類柔性附件中性面上的任意點P,則有rBP=[x,y,0]T,其中x∈[0,a],y∈[0,b],從而點P在本體系Oxyz的矢徑為
rOP=rOB+rBP=[xb+x,yb+y,0]T

(4)
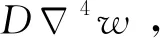
薄板單位元的慣性力為-ρhap3,根據D’Alembert原理,可得
(5)
其中,cz為板的結構阻尼系數。下面采用假設模態法求解以上偏微分方程。由于懸臂板振動的準確模態函數是未知的,因此需要尋找滿足幾何邊界條件的特征函數,參考文獻[34],可將懸臂板模態函數表示為:
W(x,y)q(t)
(6)
式中:φm(x)為懸臂梁的第m階模態函數,ψn(y)為自由-自由梁的第n階模態函數,其中ψ1,ψ2分別對應于自由-自由梁的平動模態、轉動模態。模態函數的表達式為
(7)
其中,
(8)
式中:當n為奇數時,對應于板的對稱模態;當n為偶數時,對應于板的反對稱模態。將式(6)代入式(5),兩邊乘以WT,并對全板積分,可得
(9)
式中:
分別表示板的質量和剛度矩陣,方程(9)稱為板的振動方程。根據板上任意點加速度的表達式(4),并對板進行積分,可得到板的慣性力F,以及對本體系原點慣性力矩M=[Mx,My,Mz]T的解析形式
(10)
剛體航天器的Lagrange函數為
(11)
對主剛體采用準坐標下的Lagrange方程
(12)
其中,F0,M0分別為航天器剛體受到的非保守力和非保守力矩。結合方程(9)和(12)寫成矩陣形式,可得到含有柔性附件的航天器的動力學方程
(13)
式(13)中質量矩陣的非對角部分M2表明航天器剛性平臺和柔性附件的耦合效應。由于篇幅限制,質量矩陣和廣義外力的具體形式不再給出。耦合航天器系統的動力學方程(13)和剛體運動學方程(2)構成含有太陽能帆板的航天器系統控制方程。
1.2 曲壁軸對稱儲液腔的液體晃動動力學
在軌航天器往往處于微重力環境,液體表面張力在儲腔的液體晃動中將起著不可忽略的作用。當Bond數較小時儲液腔的靜液面會產生嚴重彎曲,此外,曲壁軸對稱儲腔具有壁面不平行于儲腔對稱軸的特點,儲腔充液深度的變化導致靜液面的構形發生改變,對儲腔液體晃動動力學行為造成影響。下面考慮如圖3所示的曲壁軸對稱充液儲腔。

圖3 軸對稱儲腔示意圖Fig.3 Diagram of axisymmetrical tanks
如圖3所示,儲腔中的虛線和實線分別表示靜液面和擾動液面,分別用M,F表示;靜液面與儲液腔壁面相交的部分稱為接觸線。通過引入球坐標系統O1R1θ1φ1對儲腔液體晃動動力學進行研究,其中原點O1為圓錐的頂點,圓錐的側面與儲腔壁面在接觸線處相切。液體表面位移ζ的運動方向為R1方向。通過球坐標系,靜液面、擾動液面、儲腔壁面分別表示為:
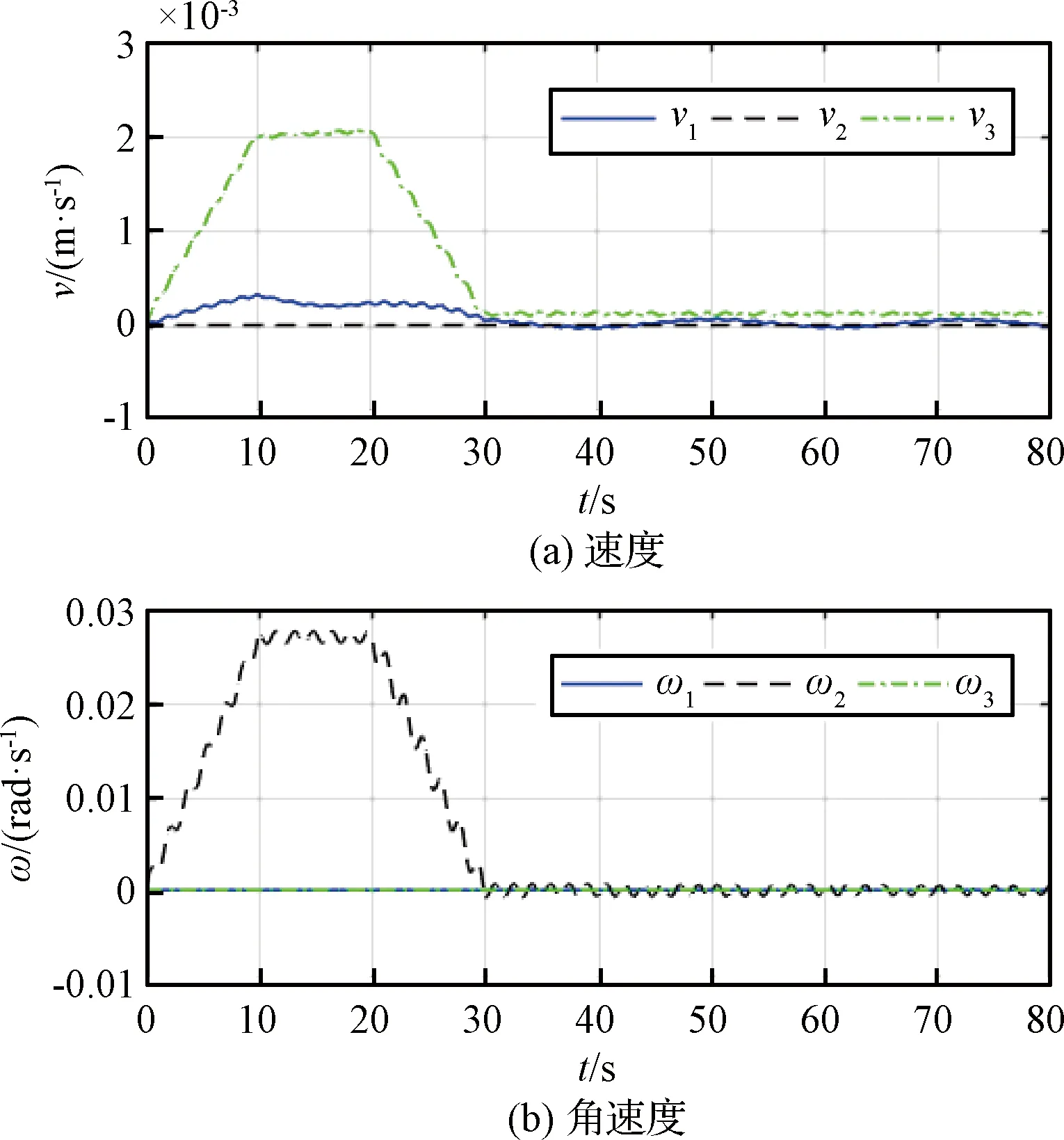
以球腔的底部頂點o1為原點,建立直角坐標系o1x1y1z1,其中o1z1軸為儲腔的對稱軸,方向向上,平面o1x1z1為球腔垂直方向剖面,即球坐標系中的O1R1θ1平面。接觸線上的任意點在直角坐標系o1x1y1z1的坐標記為(xc,yc,zc)。由于儲腔是軸對稱的,接觸線任意點到o1x1y1平面的距離都相同,即接觸線上點的zc值不發生變化。令R0為儲腔垂直方向的半徑,若zc>R0,球坐標O1的原點位于儲腔上方;若zc 對于耦合航天器系統,考慮儲腔為剛性,且液體為小幅線性晃動。儲腔液體的速度勢函數φ可通過疊加原理分解為相對晃動勢函數φr和牽連晃動勢函數φe。儲腔中任意點p的速度為vp=v+ω×·(rOo1+ro1p),則牽連晃動勢函數的表達式為 φe=(v1+ω2z0-ω3y0)R1sinθ1cosφ1+(v2+ ω3x0-ω1z0)R1sinθ1sinφ1+(v3+ω1y0- ω2x0)(h1-εR1cosθ1) (14) 對于儲腔液體晃動動力學,可通過變分原理[35]得到相應的控制方程 (15) 其中,pl,pg分別為液體和氣體壓強,σ,σ1,σ2分別為汽-液分界面F、固-液分界面W1、汽-固分界面W2的單位面積表面能,可推導得到液體相對晃動勢函數φr以及自由液面晃動波高函數ζ[11] (16) 式中特征函數Θmk的解析形式為 Θmk(θ1)=sinmθ1·G(m-αmk,αmk+m+1, m+1,(1-cosθ1)/2) 其中,G(α,β,γ,x)為Gauss超幾何級數,當|x|<1時,級數為收斂的。qm,pm為液體晃動的模態系數,amk,bmk,cmk是通過晃動頻率決定的系數,la,lb是用于提升收斂速率的系數,αmk是由儲腔邊界條件確定的常數。對式(16)關于模態系數qm,pm進行變分,代入液體晃動的控制方程(15),根據變分的獨立性,可得到模態系數的控制方程 (17) 儲液腔的液體晃動產生的晃動力和晃動力矩會對耦合航天器系統的動力學行為造成影響,同時耦合航天器系統的位置和姿態的變化也會影響液體的晃動行為。兩者相互作用,構成耦合航天器動力學系統。曲壁軸對稱儲腔的液體晃動力Fslosh和晃動力矩Mslosh是由于液體的動壓強以及表面張力動接觸線的非平衡拖動產生的,由于篇幅限制,晃動力和晃動力矩的具體形式不再給出。將晃動力和晃動力矩代入方程(13),可得 (18) 結合耦合航天器系統的運動學方程(2)和動力學方程(18),以及液體晃動模態系數的控制方程(17),構成含有板類柔性附件和軸對稱儲腔的耦合航天器系統的控制方程。 下面通過數值仿真,研究耦合航天器模型的動力學行為和各部分的耦合效應。首先驗證薄板模型的正確性,與相關文獻[36]的結果進行對比:考慮薄板繞其固定端旋轉時,薄板的變形響應。其中物理參數為:薄板的長、寬和厚度分別為a=1.8288 m,b=1.2192 m,h=0.00254 m,薄板的彈性模量為E=70 GPa,密度為ρ=2000 kg/m3,泊松比為ν=0.3。薄板定軸轉動的運動規律為 式中:T=30 s,Ω=0.2π rad/s,薄板末端角點彈性變形的響應如圖4所示,其中Case 1為本文計算的結果,Case 2為文獻的相關數據,兩者具有較好的一致性。 圖4 板的末端角點變形Fig.4 The response of corner deformation of plate 為驗證晃動模型的有效性,考慮球腔液體在橫向簡諧激勵下的晃動力響應。本文晃動模型的數值仿真結果與文獻[37]的CFD數值仿真和實驗結果進行對比。參數為:球腔半徑為R0=0.148 m,充液比為0.5,簡諧激勵的幅值為0.93 mm,頻率為0.98倍液體晃動的基階頻率。液體晃動力的響應如圖5所示,其中Case 1為本文給出晃動模型的數值計算結果,Case 2和Case 3分別為文獻[37]的CFD數值仿真結果和實驗數據。根據本文晃動模型的數值仿真結果與文獻[37]的實驗和CFD計算結果相比,在頻率和相位上有較好的吻合效果,幅值上略小于文獻[37]的結果。 圖5 球腔液體的晃動力響應Fig.5 The liquid sloshing force response of the spherical tank with the transverse excitation 下面通過數值仿真研究含軸對稱充液儲腔和板類柔性附件的航天器系統動力學行為和耦合機理。板類柔性附件是由兩塊鋁合金板面板和蜂窩狀鋁合金內芯通過樹脂粘合而成,其材料參數為[27]:長、寬、厚度分別為a=9 m,b=3 m,h=0.0262 m,剛度E=4.45 Gpa,材料密度ρ=94.5 kg/m3,泊松比ν=0.3,阻尼系數cz=0.001。航天主剛體的參數為:質量m0=5000 kg,關于航天器本體系的慣量矩陣J0=diag(1250,1250,1500) kg·m2,板的連接點位置xb=1.0 m,yb=-1.5 m。液體推進劑的參數為:儲液腔為球形儲腔,半徑R0=0.4 m,充液比0.4,液體密度ρf=1000 kg/m3,表面張力σ=0.0725 N/m,重力加速度g=0.02 m/s2,儲腔在本體系的位置(-0.1,-0.15,-0.4) m。在該參數下,液體晃動的前兩階固有頻率為0.2864 rad/s, 0.4673 rad/s,柔性附件的最低階固有頻率為2.3616 rad/s,考慮耦合航天器系統受到如下形式的零角動量的外激勵 圖6(a)、圖6(b)分別為航天器相對于慣性系的速度、角速度響應。如圖6所示,當航天器系統受到外激勵時,航天器的速度和角速度發生變化,航天器的速度分量v1,v3和角速度分量ω2不為零,而速度和角速度的其他分量為零;在外激勵結束后,航天器的速度和角速度均不為零,即航天器仍然存在平動和轉動。這主要是由于航天器剛性平臺與推進劑晃動、柔性附件振動的相互耦合效應引起的,若忽略推進劑晃動和帆板振動的影響,則航天器在零角動量的外激勵下為先加速后減速的過程,最后狀態為靜止。圖7為儲腔液面波高的響應ζx,液體晃動以一階反對稱模態為主,高階模態也會對液體晃動造成影響。液體僅存在沿著Ox方向的晃動,不存在沿Oy方向的晃動,這與外激勵作用形式和柔性附件裝配位置有關。圖8為帆板末端彈性變形的響應。當外力矩作用于航天器系統時,帆板發生振動,彈性變形的響應與外激勵的形式、作用時間有關;在外激勵作用結束后,帆板仍然存在彈性振動,由于帆板結構阻尼較小,帆板的響應為衰減振動。振動以一階對稱模態(即彎曲變形)為主,高階對稱模態也會對帆板的振動造成影響。 圖6 航天器剛性平臺的響應Fig.6 The response of rigid platform of spacecraft 圖7 液體液面波高的響應Fig.7 The response of liquid surface displacement 圖8 柔性附件末端角點的彈性變形Fig.8 The response of corner elastic deformation of flexible appendage 下面考慮帆板裝配位置的改變對于耦合航天器系統動力學行為的影響。令連接點B的位置發生變化,參數yb變為-1.25 m,其余參數均不發生變化,航天器系統受到的外激勵的形式不變,圖9(a)、圖9(b)分別為航天器相對于慣性系的速度、角速度的響應。由于帆板裝配位置的改變,導致航天器主剛體存在更為復雜的動力學響應,航天器的速度和角速度的各個分量均不為零。液體晃動參數的響應如圖10所示,圖10(a)、圖10(b)分別為儲腔液面波高在Ox,Oy方向的響應。與前一種工況相比,液體存在兩個方向的晃動,柔性附件的裝配位置的改變使得液體晃動的動力學行為更為復雜,即柔性附件與儲腔液體晃動之間的相互耦合效應。圖11為柔性附件末端彈性位移的響應,帆板的響應類似于前一種工況,但相位和幅值略有不同。 綜上所述,帆板裝配位置的改變深刻影響航天器動力學和液體晃動動力學,反應了航天器主剛體運動、柔性附件振動和儲腔液體晃動之間的復雜耦合效應。當帆板的對稱軸位于本體系慣性主軸時,帆板振動對于航天器主剛體和液體晃動動力學的影響較小,即航天器的速度和角速度的某些分量為零,且液體僅在某個方向發生晃動。 圖9 航天器剛體平臺的響應Fig.9 The response of rigid platform of spacecraft 圖10 液體液面波高的響應Fig.10 The response of liquid surface displacement 圖11 柔性附件末端角點的彈性位移Fig.11 The response of corner elastic deformation of flexible appendage 本文對含有板類柔性附件和軸對稱充液儲腔的耦合航天器系統進行動力學建模和剛-液-柔耦合效應研究。通過數值仿真,對含有帆板和球形充液儲腔的航天器系統的動力學行為進行研究。研究結果表明,耦合航天器在外激勵作用下存在復雜的動力學行為,主剛體、柔性附件、儲腔液體各部分之間存在明顯的耦合效應。在零角動量階躍驅動下,航天器主剛體的運動會引起儲腔推進劑晃動和帆板的振動,同時液體晃動和柔性附件的振動對于航天器姿態和位置有著不可忽略的影響;當躍驅動結束后,剛-液-柔耦合航天器系統仍然存在平動和轉動,若只考慮航天器主剛體運動時,剛體航天器在驅動完成后為靜止狀態;在驅動施加和撤除的瞬間,液體晃動力和晃動力矩存在不連續的變化,液體晃動和帆板振動的參數幅值存在較大的改變。柔性附件的振動以一階對稱模態為主,高階對稱模態也會對帆板的振動造成影響;帆板的裝配位置改變影響系統動力學行為,當帆板的對稱軸位于本體系慣性主軸時,帆板振動對于航天器主剛體和液體晃動動力學的影響較小,航天器的速度和角速度某些分量為零。這可為耦合航天器系統的總體設計和姿態-軌道控制器設計提供一定參考。1.3 耦合航天器系統動力學
2 仿真校驗
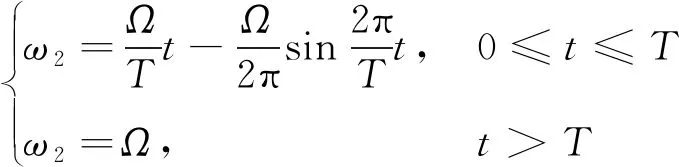







3 結 論

