泰勒級數在高等數學中的應用研究
韓冰冰
(盤錦職業技術學院基礎部,遼寧盤錦124000)
在高等數學中,泰勒級數屬于函數項級數中冪級數的一種特例。泰勒級數作為一種數學工具,能夠使數學問題變得簡單,因此常應用在理論研究和數值計算中。由于泰勒級數的知識難度較大,為了讓學生更好地掌握泰勒級數,有必要將泰勒級數知識進行詳細論述,以提高學生的學習興趣。本文將從泰勒級數的類型、展開條件、展開方法和應用出發,通過探討合理地建立泰勒級數的教學體系,以提高學生學習效果。
1 泰勒級數的類型
1.1 一元函數y=f(x)的泰勒級數
如果函數f(x)在點x0處存在直至n階的導數,那么x0的鄰域內有n階的泰勒級數[1]
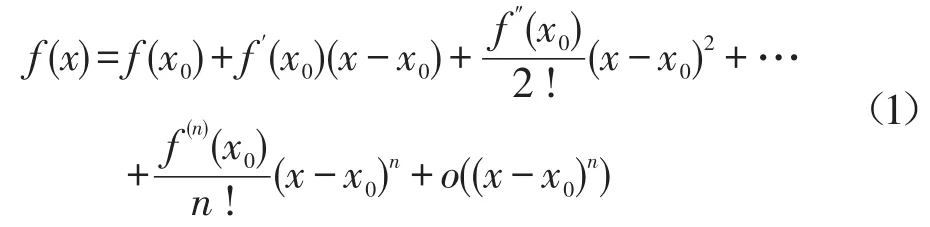
①f(x)在x0=0時,級數就是麥克勞林級數[2],即
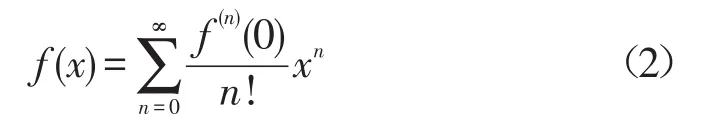
這種展開式是唯一的,而且函數f(x)的麥克勞林級數和x的冪級數是一致的。但是需要注意的是,如果f(x)在x0處有各階導數,那么泰勒級數能否在某個區間內收斂,是否收斂于f(x)仍需驗證[3]。
而泰勒級數收斂的充要條件是f(x)在x0處泰勒公式余項的極限為0,即如公式(3)[4]
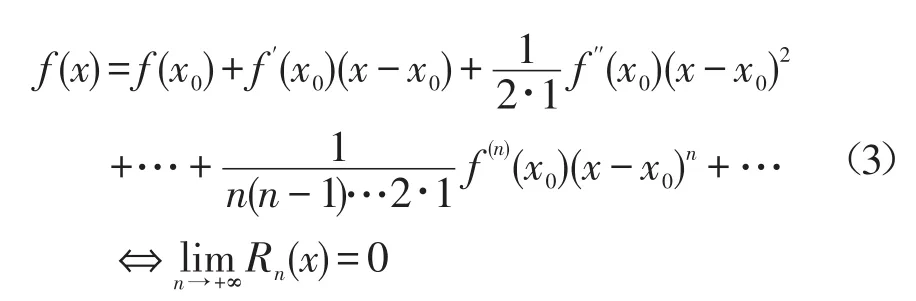
當f(x)的各階導數都存在時,即泰勒級數在收斂情況下,與泰勒公式相同,都等于f(x)。
②f(x±a)在x處展開時的泰勒級數[2]為
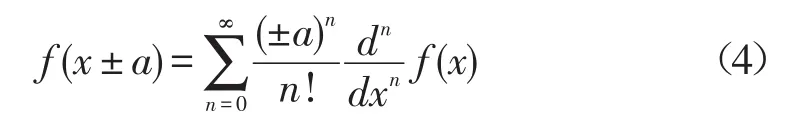
1.2 多元函數y=f(x)的泰勒級數(以二元為例)
如果二元函數u=f(x,y)在點(x0,y0)對x及y具有直到n+1階的連續偏導數[3]
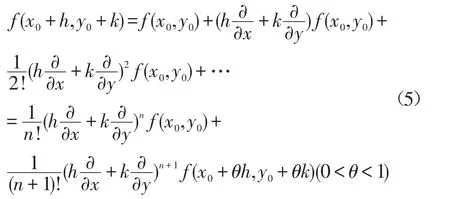
展開后就得到二元函數的泰勒級數。
下面以一元函數y=f(x)的泰勒級數為例進行說明。
2 泰勒級數的展開條件
不同函數在展開為泰勒級數時的條件是不同的。復函數f(z)展開條件比較簡單的原因是有柯西積分公式及推廣形式[5]
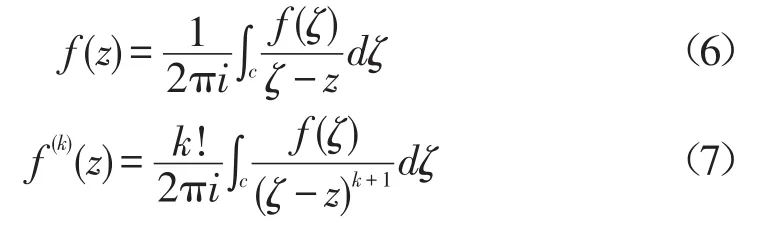
而實函數f(x)展開為泰勒級數條件很苛刻,必須具有如下條件[5]:
①f(x)在x0點存在各階導數;
②存在δ>0,使一切x,只要|x-x0|<δ,便有
其中,rn為泰勒級數的余項。
所以,在解決實函數f(x)時,可以通過復函數f(z)進行求解。
3 泰勒級數的展開方法
把函數展開成泰勒級數,主要有直接展開法和間接展開法。
3.1 直接展開法[6]
直接展開法主要分為四個步驟進行:
①求出函數的各階導數f(x),f'(x),…,f(n)(x),…;
②函數f(x)及各階導數在x=x0處的值:f(x0),f'(x0),…,f(n)(x0),…;
③寫出泰勒級數
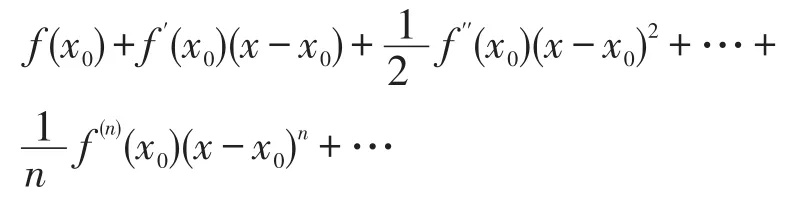
④考察余項Rn(x)在x0的某一鄰域U(x0)內的極限是否為零。
3.2 間接展開法
由于直接展開法的展開過程比較煩瑣,實際應用較少。所以泰勒級數在展開時,常用間接展開法[7]。下面就利用間接展開法來簡單介紹泰勒級數的應用。
3.2.1 函數的近似計算[8]

3.2.2 證明不等式
例2設n為自然數,試證:(當t≤n時)
證明:不等式兩邊同乘e-t,利用麥克勞林級數展開,則
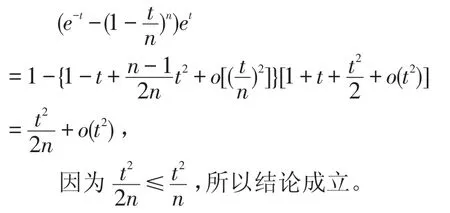
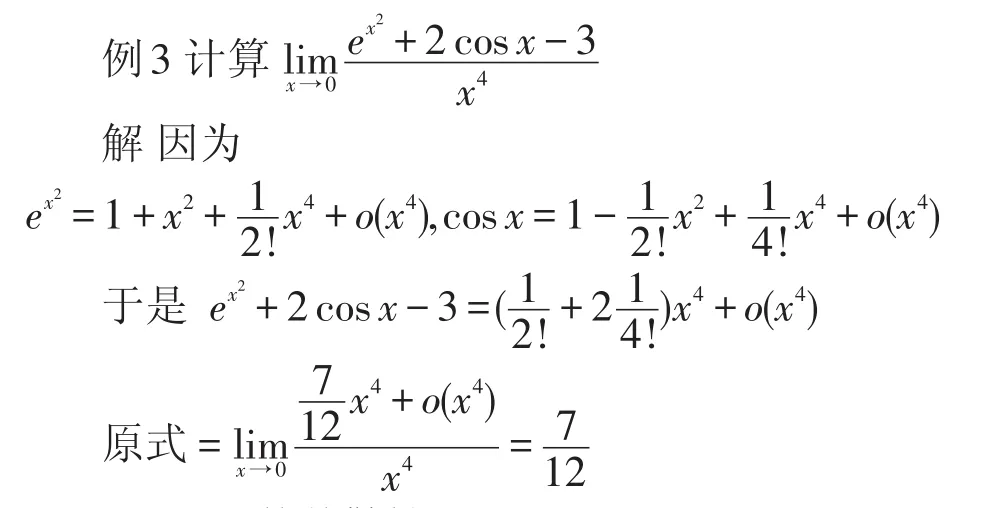
3.2.3 函數極限[4]3.2.4級數斂散性[9]


