使用費米問題來引入數學建模

【摘 要】 數學建模作為一種問題解決方式，建立起數學與現實世界之間溝通的橋梁.目前學校教育中的數學建模經過簡化無法使學生經歷完整的建模過程，其建模能力不能得到有效提高.費米問題需要學生對涉及估算的現實生活進行簡化和數學化，且在通常情況下沒有特定的解決方案，有助于培養學生數學建模能力，并給數學建模教學提供了新的思路.

【關鍵詞】 費米問題;數學建模教學;估算

近年來，人們愈發關注在課堂上引入涉及數學建模的各種活動.盡管應用和建模在大多數國家的課堂教學中比過去起著更重要的作用，但教育理念仍未統一，創新課程與日常教學實踐之間存在著很大間隙[1].數學建模作為溝通數學世界與現實世界之間的橋梁，而現實世界的變化多端也意味著學校的建模教學不能墨守成規，應在尋求多角度引入的基礎上不斷推動建模的多樣化與創新化教學.

我國于2003年頒布的《普通高中數學課程標準（實驗）》[2]中就突出強調了對學生數學建模能力培養的重要性，并且首次給出了數學建模過程的框架圖.最新頒布的《普通高中數學課程標準（2017年版）》（下稱《課標2017》）提出了數學學科六大核心素養分別為：數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析[3].其中，數學建模作為六大核心素養之一，并且同時與函數、幾何與代數、概率與統計作為四條主線貫穿高中數學課程.由此可見，數學建模在我國課程標準中的地位之高，其對學生數學能力培養的重要性也不言而喻.

《課標2017》中明確指出要讓學生經歷數學建模的整個過程，即在實際情境中從數學的視角發現問題、提出問題，分析問題、建立模型，確定參數、計算求解，檢驗結果、改進模型，最終解決實際問題.但在目前的課堂教學中，學生往往根據教師已經提供好的問題、數據進行計算求解，跳過了完整建模必須經歷的環節.這種情況一方面是由于學生目前的課業負擔較重沒有足夠的時間去體驗經歷建模的完整過程，另一方面也由于教師缺乏足夠的建模教學經驗，不能提供切合的現實情境問題去幫助學生真正地開展數學建模活動.長此以往，學生也就無法感受數學與現實間的聯系，無法提升數學建模這一重要能力.

本文將從費米問題入手，研究費米問題的良好特性以及學生在解決費米問題中所經歷的數學建模過程，探討在目前的課堂中使用費米問題來引入數學建模的重要影響.同時，也可將使用費米問題來引入數學建模看作是對當前數學建模常規化教學的一種推動與創新.

1數學建模

在數學教育中，有許多方法可以使用、研究或描述數學建模.建模過程通常始于實際問題.在對現實世界建模時，我們不斷在現實與數學之間進行切換.通過簡化，構造和理想化此問題，可以獲得一個真實的模型[4].學者Lesh和Harel提出數學模型的定義[5]，他們認為模型是用于構建、描述或解釋其他系統的概念系統，包括一個概念系統及其相應的過程.學者Borromeo Ferri將數學建模表示為整個問題解決過程（迭代和/或循環），從六個階段（實際情境、情境的心理表征、實際模型、數學模型、數學結果、實際結果）和轉換過程（理解任務、簡化/建構任務、數學化、數學工作、解釋和驗證）來描述建模過程，如圖1所展示[6].對于數學建模中的“迭代和循環”，我們可以理解為，建模的本質事實上是循環的，創建一個以抽象方式描述或表示某種現象或現實的數學模型是一個復雜的過程，該過程在不同的迭代中重復，這些迭代改進了先前得到的模型和解法，從而成為適應解決每個問題的需要.當我們在更詳細地劃分有關復雜的問題解決過程時，可以使用由Maaβ提出的“能力”的概念[4]，將建模循環劃分為子過程或子活動.在本研究中，就將利用六個建模子活動來分析學生在建模過程中的表現.

2 費米問題

費米問題一詞最早源于1938年諾貝爾物理學獎得主Enrico Fermi.他提出了關于費米問題的經典例子，即芝加哥有多少個鋼琴調音器？費米問題的定義如下：“開放的、非標準的問題，要求學生對問題情境做出假設，并在解題之前估算相關數值，這通常是一些簡單的計算[7].” Efthimiou和Llewellyn從其特殊的表述中描述了費米問題[8]，因為它總是看似分散的，且其能提供的具體信息不多，并且很少有相關特點來指引如何得到解決方案.從這些對費米問題的表述中可以看到，所謂的費米問題是一種特定類型的活動，沒有對所需解決的問題提供完整的信息，需要對涉及估算的現實生活進行簡化以及做出相應的數學化，且在通常情況下沒有特定的解決方案.為了對所呈現的情形進行詳細分析，我們需要將費米問題分解為能得出原始問題答案的更簡單的問題.

rlebck指出[9]，研究費米問題可能有助于將建模引入課堂的原因如下：（1）現實的費米問題易于被不同教育水平的學生們所接受，并且學生不需要先前學習一些特殊的數學知識;（2）促使學生構建與問題相關的信息;（3）現實的費米問題要求學生制定針對具體情境的解決策略;（4）由于現實中的費米問題不提供數字數據，所以學生必須自己估算幾個數據;（5）促進學生互相討論.

正是根據上述這些原因，以及費米問題在我國目前數學建模教學中涉及較少，本文將介紹學生在解決費米問題的過程來說明使用費米問題引入數學建模的有效性.

3 研究過程——“帝國大廈問題”[10]

學者Sriraman和Lesh曾就有關估算和費米問題中指出[11]“估算活動可以作為引發數學建模的一種方式”.學生在解決與現實相關的費米問題時，通常需要根據現實情境做出估算判斷，不同的學生可能會產生不同的解決方案，這是極富有個人特色的，而通常情況下這樣的解決過程是與前文提及的建模循環過程相吻合.也正由于解決費米問題并不需要學生具有豐富的先前建模經驗，不同水平的學生可以在不同的抽象層面上建立數學模型來解釋費米問題的實際情境，這為培養學生數學建模能力提供了良好的機會.因此，這促使我們考慮將費米問題引入數學建模教學，利用費米問題來分析學生建模過程.下面將通過一個費米問題，來展現和分析學生的解決過程.

C：嗯，有人坐過FREE FALL（是瑞典斯德哥爾摩游樂園格隆納隆德的一個景點）嗎？

A：（與B異口同聲）沒有.

C：我在想.嗯，它高90米的話，需要花費多長時間到達那？我認為需要15，20-25秒，那是90米的情況.

B：是的.

C：它（帝國大廈）一定高于200米.

研究分析 從上述過程可以看到，費米問題是在學校教育中引入數學建模的一種很好方式.所有建模子活動都在解決費米問題的過程中得到了豐富的展現，與此同時也辯證地推進了任務解決方案的發展.在解決問題的過程中，小組動態對于不同子活動的發展和激活至關重要.當面對不同的信念和觀點時，是小組中的討論和互動驅動并形成了建模過程.

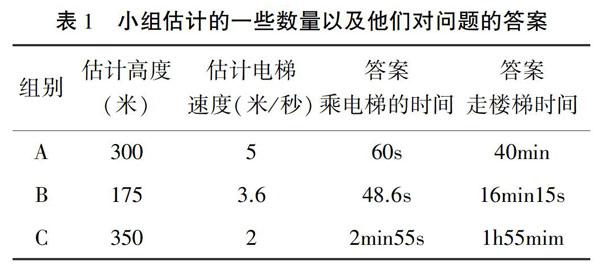
使用現實的費米問題的關鍵原因之一是它可以促進小組就問題的設定和解決方案進行討論.這些期望都在研究中得到了證實，但是研究也表明了，這類問題在一定程度上會使學生的注意力不再集中在數學本身，并且學生在討論如何估計、構造問題時走向了錯誤的解題方向.由此看來，問題的現實特征就成為了關鍵.盡管在此過程中，對數學的要求只是處于非常基礎的水平，但是可以通過明確要求一個公式來增強對數學的要求，這個公式可以是與大樓高度和使用電梯或樓梯上下耗費時間相關.4 總結與反思

回顧學生解決“帝國大廈”高度的過程，我們不難發現，當學生參與解決現實的費米問題時，他們可以完整地經歷數學建模的整個過程，并且這對于學生是否具有充足的建模經驗并無太高要求，換言之，費米問題很適合作為一種數學建模教學的引入方式.現實的費米問題來源于生活，貼近生活實際，學生在解決時需要主動對問題進行背景化并適當的引入建模元素.此外，費米問題所提供的條件和所需數據都是不充分、不完整的，而其解決方案更不是特定的、常規的，這一切問題都有待于學生親自去進行情境分析和數據挖掘.這種開放式的建模任務在一定程度上給予了學生在平時課堂中無法得到的建模能力訓練，并由此也推動了學生積極活躍地參與數學建模活動，從而產生廣泛的解決策略，促進學生數學建模能力的發展.當學生處理涉及現實生活情境或現象的情景化問題時，所有的建模能力都在建模過程中被激活了.

數學建模教育需要分階段、有系統并持之以恒地開展，同時也要形式靈活，密切聯系生產生活和社會發展的實際，用發展的眼光和熱情來調動學生的興趣[12].也正因此，結合我國目前中小學課堂中的數學建模教學特點，提出了以下建議：

首先，選擇并設計與生活實際相關的問題作為建模任務，減少刻意改編和人為加工.目前中小學生所能接觸到的與數學建模相關的問題基本是源自課本中或試卷的數學應用題，這一方面局限了學生對于數學建模的認知，另一方面也限制了學生的建模能力的發展.因為數學建模更強調的是運用所學知識來解決生活實際問題，此過程中的知識輸入和策略輸出都是動態發展的，并不同于一般的求解應用題得到明確答案的過程.學校中所提供的數學建模問題大多是具有明確條件和充足數據，符合常規的解決思路與方法，而費米問題則打破了這樣的規則，它需要學生根據個人經驗與實際情境收集數據，建立模型，通常情況下還需要經過學生之間的協作與交流才能完成最終的任務.由此，教師應該在教學過程中，減少對所謂建模性質的數學應用題的使用，增加一些可以促使學生主動收集資料，自主選擇建模方案的實際問題.

其次，教師應多鼓勵學生進行自主性探究學習、小組合作交流，減少傳統講授環節.中小學生由于課程壓力較大，時間緊迫，無法有充足的課余時間來進行自主的建模探究學習，取而代之的是教師在課堂上直接講解問題，滿足于求得最終答案即可，極大地忽略了對學生建模能力的培養.有效培養學生數學建模能力的方法就是讓學生經歷建模的整個過程，讓學生有豐富的建模體驗和感悟，而不是追求對特定問題的解答即可.當學生能夠自己對現實問題進行分析和數學化，將數學知識轉化為解決策略，其能力才可以得到提升.費米問題的解決過程，不僅是學生自主探究學習的一種體現，也是小組成員合作交流的展示.學生自己對問題的信息作出假設補充，是利用了自己的知識與經驗，而成員間對所設定的數據相互質疑、交流想法，也促進了學生學會尋找間接證據支撐自己的想法、學會多角度看待問題.這些都是數學建模所期望學生最終可以具備的能力，教師的傳統講授則剝奪了這樣一種能力的形成環節.

數學建模已經成為我國中小學數學教育中的一個重要組成部分，考慮數學建模教學的未來發展，我們應不斷借鑒國際上的優秀做法，推動我國數學建模教學的進一步創新.

參考文獻

[1]

Blum W. ICMI study 14： Applications and modelling in mathematics education—discussion document[J]. Educational Studies in Mathematics，2003，51，149-171.

[2] 黃健，魯小莉，王鴦雨，徐斌艷.20世紀以來中國數學課程標準中數學建模內涵的發展[J]. 數學教育學報，2019，28（03）：18-23+41.

[3] 中華人民共和國教育部.普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2017：4-7.

[4] Maaβ K. What are modelling competencies[J]. ZDM Mathematics Education，2006，38（2），113-142.

[5] Lesh R，Harel G. Problem solving，modeling，and local conceptual development[J]. Mathe-matical Thinking and Learning，2003 ，5（2），157-189.

[6] Borromeo Ferri R. Theoretical and empirical differentiations of phases in the modelling process[J]. Zentralblatt für Didaktik der Mathematik，2006 38（2），86-95.

[7] rlebck J B. On the use of realistic Fermi problems for introducing mathematical modelling in school. The Montana Mathematics Enthusiast，2009，6（3），331-364.

[8] Efthimio C J，Llewellyn R A. Cinema，Fermi problems and general education[J]. Physics Education，2007，42（3），253-261.

[9] César Gallart，Irene Ferrando，Lluís M. García-Raff，LluísAlbarracín，and Núria Gorgorió. Design and implementation of a tool for analysing student products when they solve Fermi problems[M]∥ Stillman G A，Wemer Blum W，Kaiser G. Mathematical Modelling and Applications： Crossing and Researching Boundaries in Mathematics Education.Seitzerland：Springer，2017：265-275.

[10] rlebck J B，Bergsten C. On the Use of Realistic Fermi Problems in Introducing Mathematical Modelling in Upper Secondary Mathematics[M]∥ Lesh R，Galbraith P，Haines C，Hurford A. Modeling Students' Mathematical Modeling Competencies. International Perspectives on the Teaching and Learning of Mathematical Modelling. Springer，Dordrecht ，2013：597-609.

[11] Sriraman B，Lesh R. Modeling conceptions revisited[J]. Zentralblatt für Didaktik der Mathematik，2006，38（3），248-254.

[12] 張平文.數學建模進入課堂已經成為世界教育的潮流[J].數學教育學報，2017，26（06）：6-7.

作者簡介

朱雨姝（1996—），女，江蘇淮安人，碩士研究生，研究方向為數學教育（指導教師：周超）.于2018年榮獲蘇州大學“校二等獎學金”，2019年榮獲蘇州大學“校三等獎學金”.