貪心二進制獅群優化算法求解多維背包問題

楊 艷，劉生建，周永權

（1.廣州大學華軟軟件學院，廣州510990； 2.廣西民族大學信息科學與工程學院，南寧530006）（?通信作者電子郵箱yangyan_08@yeah.net）

0 引言

多維背包問題（Multidimensional Knapsack Problem,MKP）是一類典型的組合優化問題，有著廣泛的實際應用價值，如項目決策與規劃、資源分配、資金預算、貨物裝載等，對其求解方法的研究無論是在理論上還是實踐中都具有一定的意義［1］。求解MKP主要有精確算法和啟發式算法兩大類：精確算法的時間復雜性都是呈指數增長的，主要用于求解規模相對較小的問題，對大規模問題依賴智能優化算法解決，常見的算法有粒子群優化算法、煙花算法、狼群算法、布谷鳥搜索算法、蟻群算法等［2-9］；進化算法多采用精英策略，在具有高進化效率的同時，存在易陷入局部最優解的局限性。文獻［2-3］提出將連續的粒子群優化算法通過轉換函數生成離散粒子群算法，并用于求解MKP，為求解離散問題提供了一種新方法。二進制反向煙花算法求解MKP具有良好的尋優效果，尤其是在背包維度高、物品數量多的問題中具有良好的尋優能力［6］；二進制狼群算法求解MKP時減小了陷入局部極值的概率［7］；二進制布谷鳥算法求解背包問題時提高了算法求解精度和收斂速度［8］；二進制蟻群算法求解背包問題時提高了算法的全局搜索能力［9］。本文受以上算法思想的啟發，通過改進獅群算法求解MKP。

受獅群協作捕獵的啟發，文獻［10］提出一種新的群智能優化算法——獅群算法，并驗證其良好的計算魯棒性和全局搜索能力，但其主要用于連續函數優化問題。本文在基本獅群算法的基礎上，引入二進制編碼，加入貪心算法增強局部搜索能力，提出一種基于貪心算法的二進制獅群算法并求解多維背包問題，通過經典算例仿真對比實驗驗證了算法的有效性。

1 多維背包問題描述

多維背包問題（KMP）可以看作多個0-1背包問題，一個m維0-1背包問題可以描述如下：

已知n個價值為，2，…，n）的物品，m個容量大小為，2，…，m）的容器，第i個物品所占第j個容器的容積大小為wij。KMP要解決的就是如何選擇物品裝入這m個容器，使得裝入容器的物品總價值最大。問題的數學模型為：

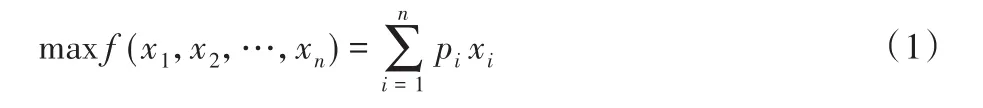
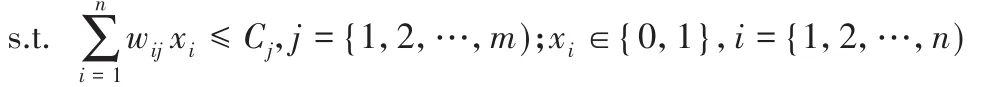
其中：f(x1，x2，…，xn)為目標函數；n為物品的編號；m為容器的編號；pi為第i個物品的價值；Cj為第j個容器的容積；wi j為第i個物品所占第j個容器的容積大小；xi為0-1決策變量，當物品i為選擇裝入時xi=1，否則xi=0。

通過引入懲罰系數將帶約束的離散化的多維背包問題轉化成無約束最優化問題，轉化后的無約束優化問題模型如下：其中懲罰系數μ是一個很大的常數，取值為1010，以保證可行解的最差值都要優于不可行解的最優值。

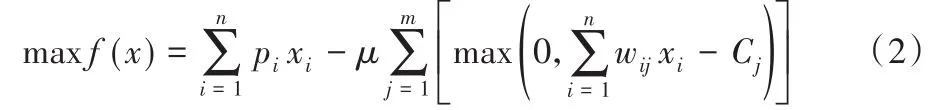
2 貪心二進制獅群算法求解多維背包問題

2.1 獅群位置數據的離散化

將獅群領地抽象為一個N×m的歐氏空間，N為人工獅的總數量，m為編碼長度；第i個人工獅在第t代的位置為為位置X i在第t代時第j維的分量值，且只能取0或1；人工獅感受到的獵物優劣即為目標函數值，通過式（2）求得。

基本的獅群算法主要適用于求解連續空間優化問題，二進制獅群算法求解多維背包問題時需將獅子的位置設為1或0，而獅子個體進行位置更新后產生的位置分量xtij不一定是1或0，使得獅群算法無法對其進行求解。由于獅子下一個位置由位置改變量ΔX i決定，ΔX i=-，ΔX i反映了的各個分量取1的概率。為了使概率值在［0，1］區間，貪心二進制獅群優化（Greedy Binary Lion Swarm Optimization,GBLSO）算法采用式（3）的轉換函數對ΔX i進行處理，然后采用式（4）對獅子位置分量置1或0操作［2，4］：

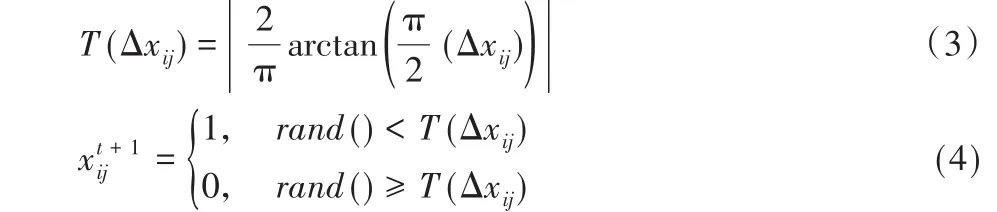
其中：t為當前代數，rand()為［0，1］上均勻分布的隨機數。

2.2 獅群位置更新規則

2.2.1 獅王位置更新規則

獅王位置是當前群體最優位置，其下一個位置通過反置移動算子計算。反置移動算子Θ(X i，M，r)表示X i在集合M指定的位置上隨機抽出r個位置進行反置運算。獅王通過在可行位置中隨機找一個位置進行取反，從而實現位置的更新，位置更新如式（5）：

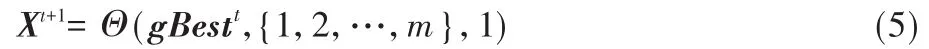
其中：t為當前代數；gBest t是當前獅群發現的最佳獵物的位置。

2.2.2 母獅位置更新規則

2.2.3 幼獅位置更新規則

幼獅向下一個位置移動的方向由一個隨機值rand（）決定：若rand（）＜0.5，幼獅在獅王附近移動進食，下一個位置由當前位置和獅王位置共同決定；若0.5≤rand()＜0.8，幼獅跟隨母獅學習捕獵，移動的位置由當前位置和所跟隨母獅的歷史最優位置決定，而所跟隨母獅由幼獅編號與母獅數量求模的方法確定；否則幼獅將被逐出獅群，即幼獅向獅群當前最優位置的相反方向移動。幼獅位置更新如式（7）所示：

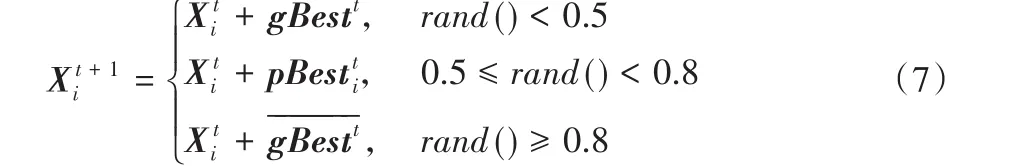
2.3 貪心算法修正處理

由于獅子的初始位置是隨機產生的，在解空間會產生一部分不滿足約束條件的無效解，若直接使用式（2）計算適應度，其結果必然會小于零，從而造成大量的無效試探。為了縮短尋優時間，可對任意一個潛在解使用貪心算法進行修正，使其轉換為一個可行解。使用貪心算法修正會增加算法的計算量，但能夠使搜索有一定的導向而不再盲目，反而能在總體上縮短處理時間。設第i個潛在解的位置為Xi=(xi1，xi2，…，xij，…，xim)（1≤i≤N，1≤j≤m），貪心算法修正潛在解的實現步驟如下：

步驟1 對任意一個容器j，用式（1）檢測輸入值Xi表示的物品體積是否超過Cj，若否，則直接轉入步驟3。

步驟2 循環處理（總體積＞Cj時）：

1）從袋中取出價值最小的物品xij；

2）實際總體積減去該項物品體積，置xij=0。

步驟3 循環處理（總體積＜Cj時）：

1）從候選物品中選擇價值最大的物品xij；

2）若該物品的體積加上袋內物品總體積＞Cj則結束循環；

3）把該物品加入袋中，并更新總體積，置xij=1。

步驟4 返回修正后的X i。

步驟5 檢測下一個容器，直到m個容器中的物品全部檢測完成。

3 GBLSO算法

GBLSO算法步驟如下：

步驟1 初始化。設定獅群數目N，最大迭代次數T，維度空間m，母獅占獅群比例因子β，隨機產生獅子的初始位置X i，貪婪因子Qi。

步驟2 計算適應度值。根據適應度值排序獅王、母獅及幼獅的位置，適應度最佳的位置設為群最優位置，即獅王位置。

步驟3 判斷終止條件：若達到終止條件，則輸出問題最優解，即獅王的位置；否則，轉步驟4。

步驟4 根據式（5）、（6）、（7）更新獅王、母獅及幼獅的位置。

步驟5 根據獅子的位置計算適應度值，并對無效位置進行糾正處理。

步驟6 更新獅子自身歷史最優位置及獅群歷史最優位置。當有獅子發現最優解時，其他獅子調整自己的貪婪因子為自身因子和最佳因子的均值。

步驟7 每隔一定迭代次數（10次）重新排序獅王、母獅及幼獅的位置。

步驟8 計算適應度值，并判斷算法是否達到終止條件，若達到則輸出問題最優解，否則轉步驟4。

4 仿真實驗與分析

本文選取經典的離散二進制粒子群優化（Discrete binary Particle Swarm Optimization，DPSO）算法［11］和二進制蝙蝠算法（Binary Bat Algorithm，BBA）［12］，并按照本文中的修復機制進行改進，和本文算法進行比較。本文算法的實驗硬件環境為Intel Xeon E3-1230V2@3.30 GHz和16 GBDDR3內存，操作系統為Win10，使用python3.7，NumPy進行實驗仿真。

4.1 常用算例測試

為了驗證二進制獅群群算法求解多維背包問題的有效性，本文選用參考文獻［11］中的5類10個算例，每個算例的背包維度和物品數量如表1所示。

表1 選用算例測試表Tab.1 Test tableof selected examples

4.2 算法參數設置

實驗中種群規模N=50，最大迭代次數T=200。各算法的特定參數設置如表2所示。

表2 算法參數設置表Tab.2 Settingsof parameters of different algorithms

4.3 仿真實驗及結果分析

對每個算例獨立運行20次，記錄20次實驗中獲優次數、最優解、最差解、平均解和尋優成功迭代次數，如表3所示。

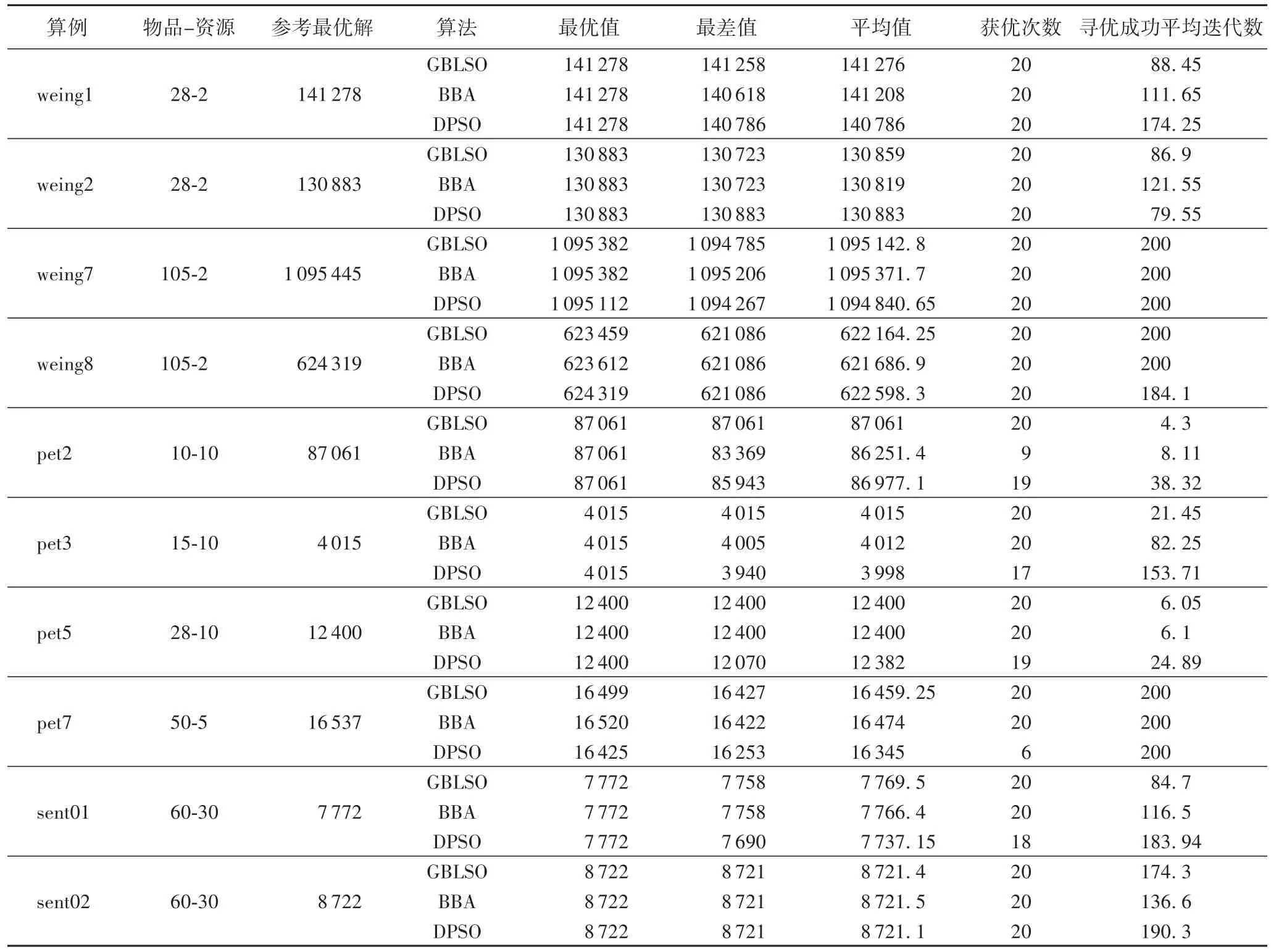
表3 三種算法性能比較Tab.3 Performancecomparison of threealgorithms

從表3的對比數據可以看出，本文算法在大多數算例上都要優于BBA和DPSO。本文算法每次迭代都能獲得最優解，且尋優平均迭代數較參考文獻算法少；說明本文算法收斂速度快，效率高。

圖1是GBLSO、BBA和DPSO三種算法獨立運行20次實驗的平均尋優曲線。限于篇幅，僅給出三種算法對不同維數的背包問題部分算例的平均尋優曲線圖。從圖中可以看出，本文算法的平均尋優收斂速度快，能更好地找到全局最優解。

圖1 典型測試算例尋優曲線Fig.1 Optimization curves of typical test examples

5 結語

本文在獅群算法的基礎上引入貪心算法的思想，利用二進制編碼，提出了一種基于貪心算法的二進制獅群算法，并用于求解多維背包問題。通過10個經典多維背包算例的仿真對比實驗表明本文算法具有較好的求解穩定性、收斂性和全局搜索能力，同時改進算法也為其他二進制的離散優化問題提供了一種有效的方法。