面向GPU 平臺的二維FFT 的加速技術研究

陳博倫，何衛鋒

（上海交通大學微納電子學系，上海200240）

0 引言

快速傅里葉變換（Fast Fourier Transform，FFT）算法是圖像處理的基礎算法之一，廣泛應用于圖像濾波、圖像降噪、圖像壓縮等領域，同時也是基于頻域分析的圖像處理算法的基礎。因此，針對FFT 運算的硬件加速對提升系統性能有重要的意義。

主要的硬件加速平臺包括圖形處理器（Graphics Processing Unit，GPU）、現場可編程邏輯門陣列（Field Programmable Gate Array，FPGA）等。其中，GPU 因其先進的并行架構體系，能夠支持海量的多線程、高內存帶寬以及大計算能力，在數千個核心上分配大規模多線程，并行執行獨立任務而備受青睞。由于FFT 算法往往具有計算并行度高、數據流規整的特點，可以有效發揮GPU 大規模并行計算的潛力，因而受到了廣泛的關注。

張全等人[1]分析了全局內存合并訪問事務大小與GPU 占用率的關系，優化了二維FFT 算法在GPU 上的全局內存訪問效率，使GPU 上二維FFT 算法的運行速度達到CUFFT 6.5 的1.3 倍。Govindaraju 等人[2]介紹了分層混合基數FFT 算法，有效利用了GPU 上的共享內存作為FFT 逐級運算時的緩存。另外，使用一些基于GPU 平臺開發的商用算法庫可以方便快捷地實現圖像處理加速。例如NVIDIA 發布的CUDNN 算法庫，能提供相關的函數接口，而且能自動適應不同的GPU 硬件平臺，可移植性強[3]。然而，這些算法庫都是閉源的，無法對其進行修改、分解和組合，靈活性差，不能適應所有的應用場景。

1 GPU上一維FFT算法的整體結構設計

1.1 算法原理

本文選取Cooley-Tukey 算法來實現FFT。Cooley-Tukey 算法是最常見的FFT 算法之一，其原理是用多個長度較小的離散傅里葉變換（Discrete Fourier Transform，DFT）來計算長度較大的DFT，經過反復迭代，最終分解成多個最小尺寸DFT。這個最小尺寸DFT 稱作蝶形運算單元，而最小尺寸稱作基數。在這基礎上，根據基數的性質，又有高基和分裂基等多種算法。FFT分解基數的大小決定了分解后的級數。

圖1 展示了以2 為基數的8 點Cooley-Tukey FFT算法，蝶形運算結構共3 級。最后一級的輸出結果是順序的，而第一級的輸入序列的順序需要重新排列，稱為倒序排列。每個蝶形運算單元有自己的旋轉因子，蝶形單元的輸入需要先乘上對應的旋轉因子，再進行蝶形運算。旋轉因子的底數取決于FFT 點數，而指數與蝶形單元所在的級數及其本身的序數有關。

圖1 基-2 Cooley-Tukey FFT算法

1.2 算法整體結構設計

基于一維FFT 算法的原理，我們首先分析一維FFT 算法的可并行性。以單一基數的一維FFT 為例，假設基數為R，長度為N=RM的FFT 算法運算結構共M級，每級包含N/R 個蝶形單元。同一級的蝶形單元互不相關，可并行執行。但后一級的蝶形單元的輸入數據來源于前一級中R 個相關蝶形單元的輸出數據，相鄰兩級存在依賴關系，不可并行，必須按順序串行執行。

根據上述分析結果，本文設計了一維FFT 算法在GPU 上的并行實現過程，如圖2 所示。圖中的主要模塊包括分解基數選取、倒序排列、旋轉因子計算以及蝶形運算。分解基數的選取決定了每一級的蝶形運算結構。每一級的基數不必相同，基數不同時，蝶形單元的結構也不同。倒序排列發生在輸入序列的讀取階段。每一級中的蝶形單元結構相同，但是指向不同的內存地址。兩級蝶形結構之間通過共享內存進行數據通信。

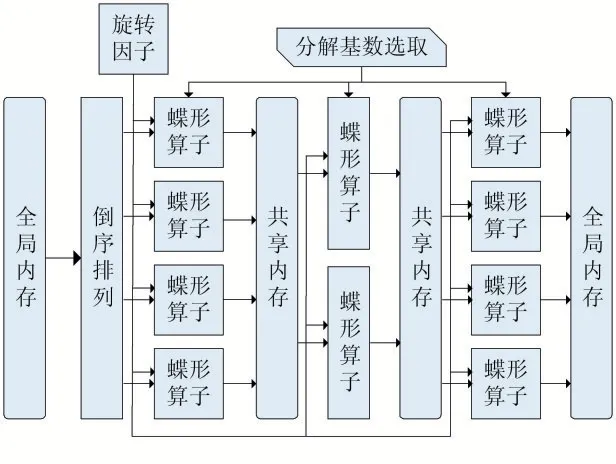
圖2 GPU上一維FFT算法并行實現過程

（1）旋轉因子計算：使用常量內存查找表或CUDA內置函數庫中的快速三角函數__sinf（）、__cosf（）來得到旋轉因子θ的三角函數值。比較設備的運算能力和常量內存的帶寬大小，從而決定到底使用哪種旋轉因子θ的計算方式。計算密集型內核采取查找表方法，內存密集型則采取實時計算方法。

（2）倒序排列：倒序排列會導致全局內存的不連續訪問。線程束中的線程訪問全局內存不連續時，GPU會發出超過原本次數的訪存事務，稱為全局負載重播。全局負載重播會消耗過多的內存帶寬，導致嚴重的性能問題。不產生負載重播的全局內存訪問稱為合并訪問。設計中引入一級額外的共享內存作為緩存，在此緩存空間中進行倒序排列，之后倒序的序列傳向后遞到第一級蝶形運算結構。這種方法實際上將不連續的內存訪問風險從全局內存轉嫁到共享內存。幸而共享內存在不連續訪問的情況下仍然可以實現較高的帶寬利用率，從而解決全局內存訪問不連續的問題。

（3）蝶形運算：蝶形運算包括兩個部分：共享內存訪問和運算。運算是簡單的乘累加運算，而共享內存的訪問則較為復雜。因為每一級蝶形結構的訪存跨度在不斷變化，所以共享內存訪問過程中極容易發生bank conflict。以圖1 為例，每一級蝶形單元的地址訪問跨度Ns 依次為1、2、4，均小于32，因此線程有可能同時占用兩個或以上的存儲體，導致共享內存發生bank conflict。為了避免上述問題，本文設計了以蝶形單元訪存跨度為依據的共享內存訪問方式，寫入數據時，每隔R×Ns 個數據填充一個無效數據。

（4）分解基數選取：FFT 算法分解過程中，基數越大，蝶形單元的級數越少，則同步操作次數越少，而且內存的訪問次數降低。但是大基數也存在相應的劣勢，基數越大，每個蝶形單元的規模更大，計算量更高，占用寄存器數量越大。由此可以推斷，隨著基數的增大，程序的性能瓶頸從內存密集型過渡到計算密集型。

比較GPU 設備的共享內存帶寬和浮點運算吞吐量，可以定量分析FFT 的并行效率，從而選擇合適的基數進行分解。另外，GPU 寄存器數量的限制意味著大基數分解的FFT 往往是不可取的，減少線程數可以減少寄存器占用的總數和使用的共享內存的數量，但是線程太少，線程束數量不足以隱藏訪存延遲。

一個大小為R 的蝶形單元的浮點運算次數為5·r·R，其中r=log2R，每級共N/R 個蝶形單元，其理論運算時間如下所示，其中ComputeCapability 是GPU 的浮點運算能力。

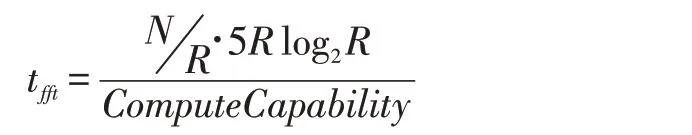
假設數據緩存在共享內存，而且共享內存的訪問效率為100%，那么共享內存訪問的理論時間如下所示，其中DataWidth 是數據位寬，Bandwidth 是共享內存帶寬。

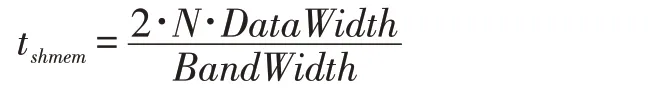
圖3 展示了共享內存訪問和蝶形運算理論性能的比較。假設訪存時間與運算時間相等時的基數等于Rx，此時內核同時達到共享內存帶寬瓶頸以及計算單元運算速度瓶頸；當基數小于Rx 時，內核性能受限于共享內存有效帶寬；當基數大于Rx 時，內核性能受限于GPU 運算能力。

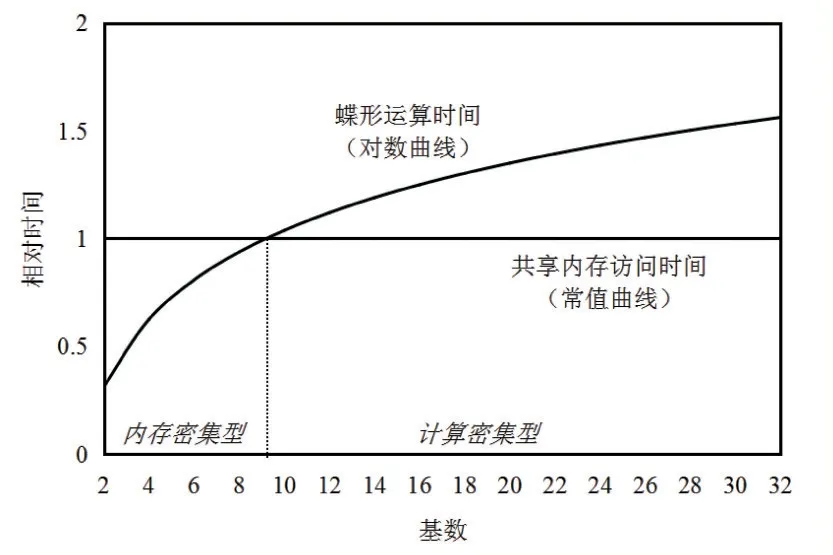
圖3 共享內存訪問和蝶形運算的理論性能比較

2 GPU上二維FFT算法的并行設計

二維FFT 可以分解成行方向一維FFT 和列方向一維FFT。行變換和列變換不能同時進行，必須先完成其中之一，再進行另一變換。從整幅圖像變換的可并行性來看，每一行或列的變換可以并行執行，即將圖像的行或列變換分解成與圖像行或列數相同的一系列獨立的一維FFT 任務，然后將這些任務分配給線程塊或線程。這些任務可以有限地合并在一起，因為圖像任意兩行或兩列的一維FFT 的算法結構完全相同，可以共享旋轉因子，從而減少旋轉因子的計算次數。

一維FFT 的并行實現已在前文給出，在此基礎上實現二維FFT 的關鍵是對全局內存的訪問。全局內存中地址連續的數據被同一個線程束中的線程訪問，而且滿足內存對齊條件時，這些內存訪問請求會被合并。合并的內存區間越大，全局內存的訪問速度越快。GPU支持32byte、64byte、128byte 的合并內存模式。

行變換時的全局內存訪問是連續的，如圖4 所示。基數為16 的1024 點序列分割成16 個字段，每個字段長度為64。64 個線程依次順序讀取每一個字段到共享內存，然后進行一維FFT 運算。因此，行變換時的全局內存訪問滿足內存合并的要求，其帶寬利用率理論上為100%。但是當基數增大時，每個字段的長度也相應地減短，導致線程數量減少，不利于程序實現充分的線程級并行。

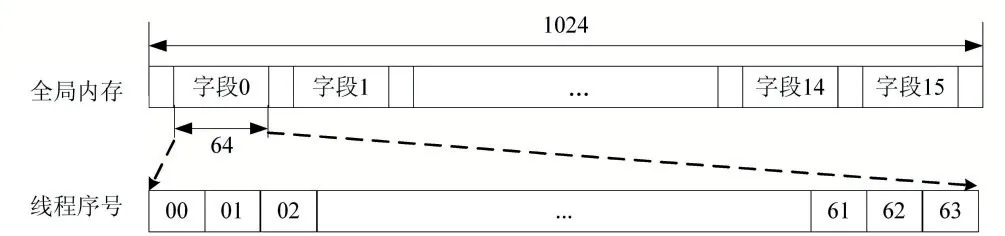
圖4 行變換時的全局內存訪問

列變換時，全局內存訪問不再連續，這會導致訪存效率顯著降低。為了提高訪存效率，本文重新設計了列變換時的全局內存訪問模式，使其滿足內存合并條件，如圖5 所示。線程塊同時讀取多列數據，當每個數據寬度為8Byte 時，連續4 個線程讀取的數據合并為32Byte，滿足最低限度的內存合并要求。

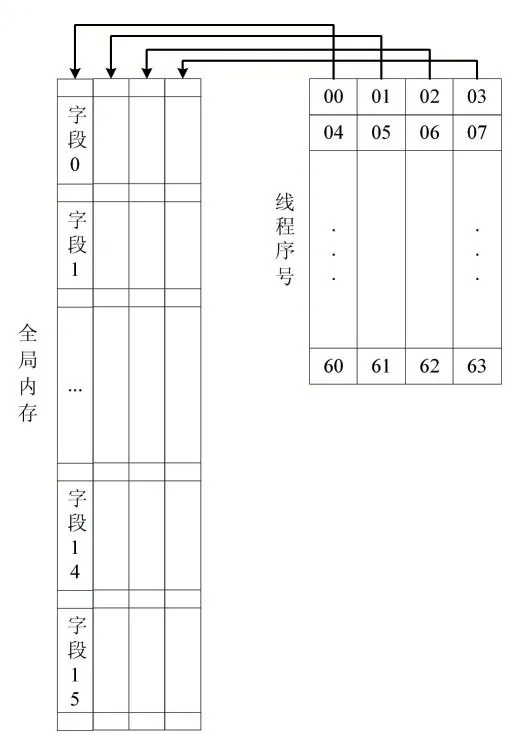
圖5 列變換時的全局內存訪問

3 二維FFT算法的性能測試結果及分析

實驗使用的硬件平臺為JETSON TX2，其搭載的Tegra X2 SoC 配置及性能如表1 所示。

表1 Tegra X2 配置及性能

首先進行二維FFT 的行變換和列變換的性能測試。二維圖像的尺寸為1024×1024，每個數據的位寬為8Byte。其中行變換采取不同的數據訪問模式，分別是32bit、64bit 以及128bit，研究數據訪問模式對性能的影響。列變換采取不同的批量處理列數，研究批量處理的數據列數對性能的影響。列數越大，意味著同一個線程束中合并訪問全局內存的線程越多。由于FFT 的運算量較低，理論運算時間與內核實際執行時間相比幾乎可以忽略不計，因此這里使用全局內存的有效帶寬來表征內核的性能。

基于上述測試方法得到的行變換性能如圖6 所示。線程數量從32 增長到256 時，內核的性能有了10.5%至43.5%不等程度的提升。這是因為占用率逐漸增大，線程級并行度逐漸升高。隨后線程數量繼續增長，內核性能又降低了9.5%到11.4%。這是因為占用率不再增大，而線程的指令級并行度卻逐漸降低。從不同數據訪問模式的性能來看，64bit 和128bit 數據訪問模式的性能相近，而二者的性能相比32bit 訪問模式提升了15%左右，說明內核開發時應當盡可能選擇64bit 和128bit 數據訪問模式。如果數據位寬小于64bit，則應該將多個數據合并讀取，從而提高全局內存訪問速度。

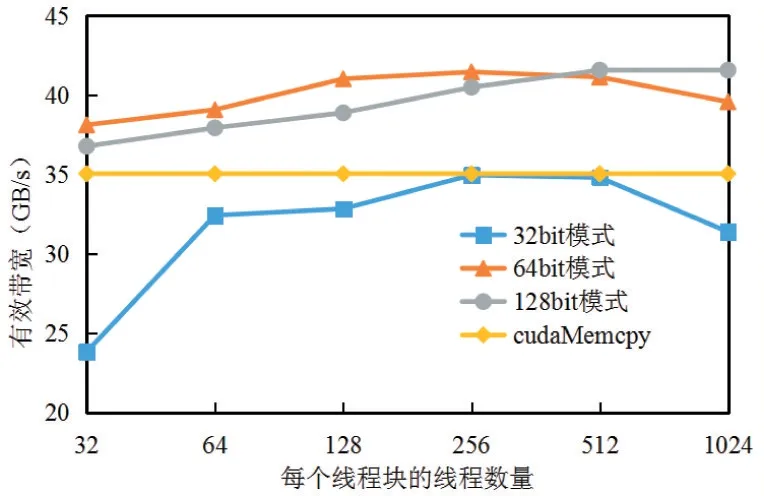
圖6 行變換性能測試結果

同理，我們進行了列變換的性能測試，結果如圖7所示。隨著線程束內合并訪問全局內存的線程數量上升，內核性能有著300%左右的顯著提升。當合并訪問的全局內存寬度大于64Byte 后，性能趨于穩定。列變換中，全局內存的峰值有效帶寬達到41GByte/s，與行變換時的帶寬相同。因此本文的二維FFT 算法已經充分發揮了GPU 存儲器的有效帶寬，實現了峰值性能。

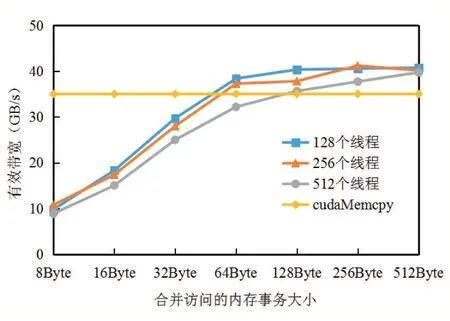
圖7 列變換性能測試結果

基于行變換和列變換的性能測試及分析結果，我們接下來測試二維FFT 算法整體的性能，并將其與CUFFT 庫函數的性能作比較，結果如圖8 所示。隨著圖像尺寸的增大，FFT 算法的運算吞吐率逐漸升高，1024×1024 尺寸下的運算吞吐率相比128×128 尺寸提升了將近400%。當尺寸繼續增大，運算吞吐率的增長幅度開始變緩，4096×4096 尺寸下的運算吞吐率相比1024×1024 尺寸只提升了42%。

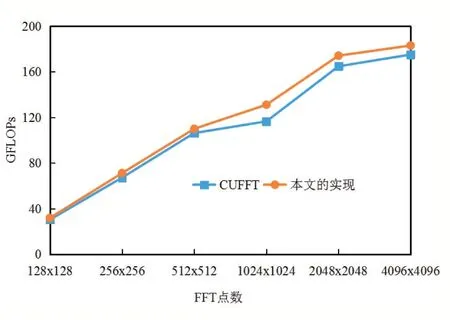
圖8 使用庫函數與本文方法實現二維FFT的性能比較

隨著二維FFT 的尺寸繼續增大，運算吞吐率很難再繼續提升，小范圍內有可能反而會降低。因為隨著尺寸增大，共享內存空間需求在不斷增大，直至達到臨界點。此時最大共享內存空間無法滿足一次行變換所需，需要引入全局內存作為緩存。這意味著算法訪問全局內存中的次數增多，會導致程序運行時間顯著上升。

4 結語

本文首先分析了FFT 算法的并行性，提出了GPU上一維FFT 算法的整體結構設計，并介紹各個主要模塊的高效實現方法。隨后提出了批量列變換機制，解決二維FFT 列變換時全局內存訪問無法合并的問題。最后，進行二維FFT 的性能測試，并與CUFFT 庫函數的性能進行比較，驗證本文的研究成果。