錨桿錨固質量等級快速評級方法研究
王開華,楊森,周繼中,曹其壯
(中國水利水電第七工程局有限公司,成都611730)
0 引言
在工程實踐中,錨桿支護技術廣泛應用于地下洞室、隧道支護工程及高邊坡治理工程[1],其質量的無損檢測通常采用聲波反射法[2-4]。錨桿質量等級主要分為A、B、C、D 四類[5],其中A 級和B 級確定為合格,C 級和D 級確定為不合格,其依據如表1 所示。
如表1 所示,規程中僅給出了錨桿錨固密實度和等級的定性判別標準,許多地方用詞較為模糊,如“桿底反射信號微弱”、“有較弱的缺陷反射波”、“清晰的桿底反射波”,在實際應用中不容易掌握相應的尺度,而且標準要求同時識別時域信號特征和幅頻信號特征,這在一定程度上增加了計算量和識別難度。因此,為了便于計算機程序對錨桿錨固的質量等級進行定量識別,本文嚴格遵循錨桿密實度質量評判規程,提出了一種基于閾值評級的錨桿錨固質量等級快速評級方法,該方法僅針對錨桿的桿底反射的時域信號進行處理,便能滿足分類標準要求,且具有簡單、高效、準確的特點。
1 算法概述
1.1 數據預處理
由于錨桿反射信號原始數據存在長度不一致,采樣間隔不一致等問題,無法直接用于算法處理,因此在進行分類之前,需對原始數據進行一系列預處理操作,使得用于分類處理的輸入數據是經過歸一化的可以相互比較的完整數據。而且預處理操作,可提升算法的正確性和分類的準確性。
(1)原始數據歸一化以及獲取相似度矩陣
原始數據的歸一化處理過程包括Y 方向和X 方向的歸一化。Y 方向的歸一化是振幅歸一化,即將反射信號的縱坐標歸一化到設定的振幅區間。X 方向的歸一化是時間歸一化,即將以不同采樣間隔獲取的原始數據,通過曲線擬合和重采樣的方法歸一化到同樣的采樣間隔。歸一化的作用是排除激蕩信號大小的不同和錨桿長度的不同對后續算法的影響。

表1 錨桿密實度質量等級分類依據
現有儀器會對每根錨桿進行六次不同的測量作為一組數據,個別同組原始數據會含有異常數據,為了排除異常數據的影響,本文采依據公式(1)計算同組數據的兩兩相似度,并組成相似度矩陣,將比較突出的異常數據篩除。
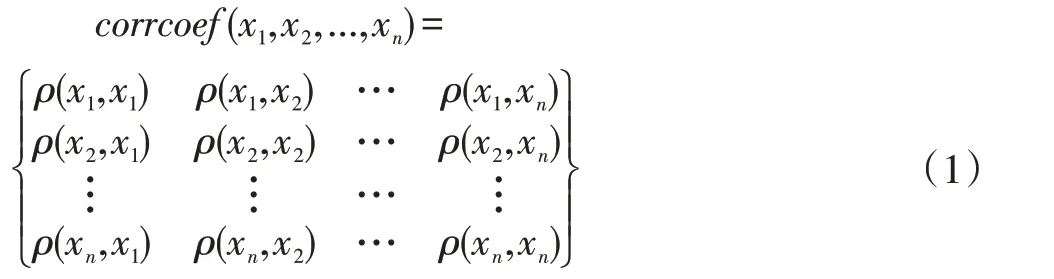
其中xi(x=1,2,…6)表示某根錨桿的六次測量數據,corrcoef(·)表示計算相似度矩陣,ρ(m,n)表示計算m、n 的相似度,本文通過公式(2),計算m、n 的相似度:

其中μm,σm分別是m 的均值和標準差。
在同一根錨桿上采集的數據不應該有較大的差別,任意兩組數據的相似度應為0.9 以上。如果某數據與同組的其余數據相似度均不足0.9,那么將該數據視為異常數據排除,保留剩余數據。如果某組中有多于兩個異常數據,那么將整組數據視為異常數據排除。
(2)x 方向修正以及上下峰值預處理
本文所述算法需要獲取歸一化后的曲線x、y 值以及上下峰值分別對應的坐標值,上下峰值即在發射信號的波形圖中,正方向的峰值稱為上峰值,在負方向的峰值稱為下峰值,在后續計算中上下峰值分別計算。
由于現場測量時,激振信號的強度和持續時間的不同,會導致反射信號的主頻率或周期不同,從信號的波形圖上分辨,則表現在不同測量時,x 方向的峰值間隔不同,如圖1 所示,同一個樣本1-(14)內的兩組數據1-(14)_1 以及1-(14)_4 相比較而言,從視覺上就可以看出曲線1-(14)_1 的峰值間隔與曲線1-(14)_4 的峰值間隔并不相同。為了便于后續計算和比較,需要將其統一到一個基準上進行計算,即進行x 方向上修正。
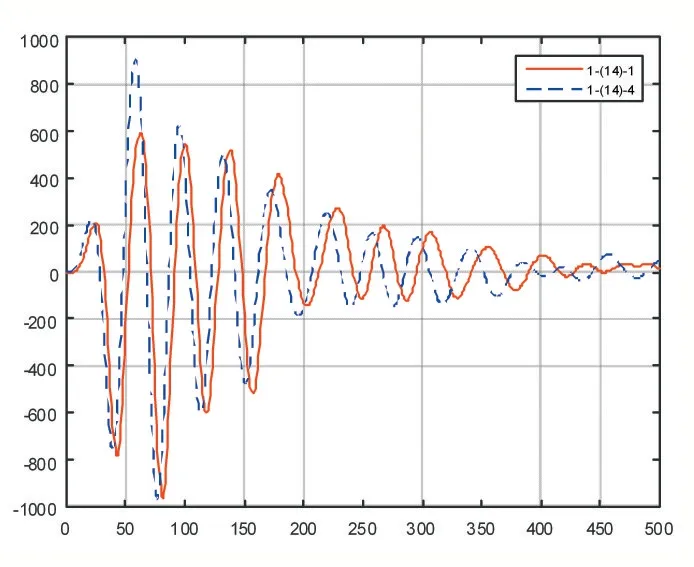
圖1 修正之前的樣本數據曲線
具體修正過程如下:
①獲取曲線的前三個上峰值點p1,p2,p3;
②計算峰值橫坐標間隔平均值:

其中,pix表示峰值pi的橫坐標,將pavg設置為修正系數;
③對全部點的橫坐標值進行修正:

其中,xbefore、xafter分別表示修正前后的橫坐標值。
同時,由于激振信號等原因,可能出現第1 個上峰值或下峰值未達到該方向最大的情況,在后續峰值比較時該峰值不具備參考意義,需要去除該峰值,使其不參與后續峰值計數和處理。
1.2 閾值分類方法
在具體分類過程中,由于A、B 類波形曲線比較相似,C、D 類波形曲線比較相似,而AB 類與CD 類相比較而言,波形相差較大,如圖2 所示,故采取由粗到精的分組分類策略,先將A、B 類視為一組,C、D 類為一組,完成分組分類后,再依據各類別特征具體分為A、B、C、D 種等級。
首先AB 類波形規整,只在前段有較大起伏,而CD 類波形較散亂,因此可通過曲線后段部分峰值均值作為分類依據。分別獲取上下峰值點數組[u1,u2,…,um]和[d1,d2,…,dn]。以上峰值為例,將從ui開始的后續x個峰值點用于計算,下峰值點同理。
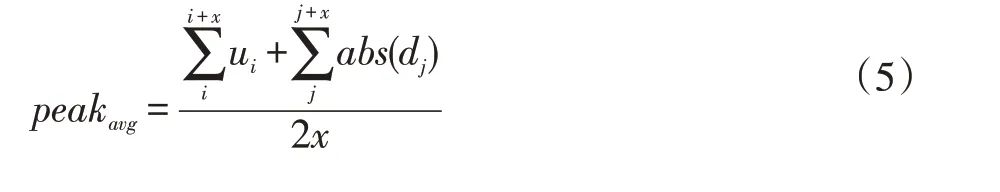
依照公式(5)獲取峰值均值,其中abs()表示求取絕對值。將peakavg作為區分AB 類和CD 類的依據。
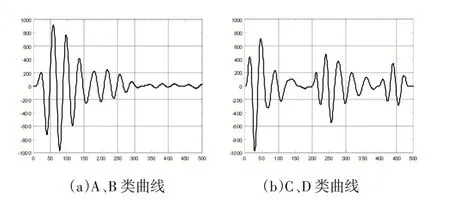
圖2 樣本數據波形曲線
其次C、D 類的劃分根據為其后半段波動起伏情況,與D 類數據相比,C 類數據后段峰值起伏相對較小。計算曲線上下峰值最大值與最小值的比值ratio,并聯合peakavg,劃分C、D 類數據。
而A、B 類的具體劃分依照其曲線波形規則程度。A、B 類曲線前部分起伏較大,而后面部分波形平整,如圖3 所示,皆為包括最高峰開始的前4 個峰這段曲線波動起伏明顯,而其后的曲線波動較小,基本趨于直線狀態。因此對于A、B 類的劃分就可以分別從曲線后半段波動起伏程度以及曲線前半段波形下降狀態著手。
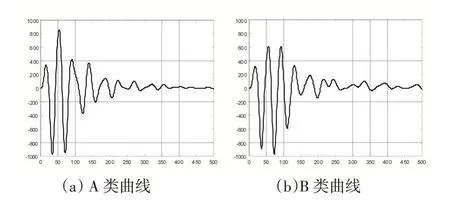
圖3 A、B類曲線
以上峰值為例,將曲線最高峰后的第z 個上峰后的部分視為后半段,曲線后半段的波動起伏程度可根據后半段的前p 個峰值均值來進行確定。接著對于曲線前半段,計算上峰值最高峰開始的第1 個峰值與第2個峰值連線k12 的斜率絕對值以及第1 個峰值與第4個峰值連線k14 的斜率絕對值,將這兩個斜率值作為判定依據,如圖4 所示。
2 具體實驗結論與分析
通過對實際工程運用中的錨桿進行測量,獲取了本文實驗所需的反射信號。共對351 根錨桿進行測量,每根錨桿測量六次,作為一組原始數據保存。然后使用人工分類方法,按照規程[5]對每組錨桿進行等級判斷。

圖4 斜率絕對值計算示意圖
再完成人工篩選后,對原始數據按照第二章所述方法進行預處理得到中間數據。先進行分組分類。實驗中,i 取值為5,x 取值為6。根據公式(5),計算峰值均值peakavg,若此峰值均值大于或等于閾值130,則說明該曲線波動較大,判定該曲線屬于C、D 類,否則,該曲線屬于A、B 類。
其次對于C、D 類的具體劃分,除了計算峰值均值,同時還計算上下峰值最大值與最小值的比值ratio,并聯合峰值、峰值均值以及比值作為分類依據。若峰值均值peakavg大于或等于閾值200,則判定該曲線屬于D類;反之,若峰值均值peakavg在閾值130-200 范圍內,同時滿足上峰值最大值大于130 且下峰值最大值大于150,且其比值大于或等于閾值10,則判定該曲線屬于C 類。
最后對于A、B 類的具體劃分,在針對曲線后半段波動起伏程度以及曲線前半段波形下降情況的定量描述中,除了之前已獲取的峰值均值,還需計算從最高峰開始的上下峰值的第1 個峰值與第2 個峰值連線的斜率絕對值abs(k12)以及第1 個峰值與第4 個峰值連線的斜率絕對值abs(k14)。
根據峰值、峰值均值以及斜率絕對值的統計結果,可知當曲線除包括最高峰開始的前4 個峰值以外的后6 個峰值均值在閾值范圍60 以內,且滿足嚴格連續下降趨勢,即曲線前4 個峰值連續遞減;或呈總體下降趨勢,即曲線上下峰值的第1 個峰值與第2 個峰值連線斜率的絕對值大于第1 個峰值與第4 個峰值連線的斜率絕對值,且除最高峰外的前3 個峰值之間的差值絕對值小于閾值50,滿足上述條件的曲線即為A 類曲線。
當曲線從第5 個峰值開始的后6 個峰值均值在閾值范圍60-130 以內,曲線前4 個峰值并不滿足嚴格下降趨勢,而是滿足曲線上下峰值的第1 個峰值與第2個峰值連線的斜率絕對值大于第1 個峰值與第4 個峰值連線的斜率絕對值,但是從曲線第2 個峰值開始,直到曲線的第5 個峰值結束,這個范圍內的曲線峰值兩兩之間差值的絕對值大于或等于閾值50,這樣的曲線即為B 類曲線。
3 結語
本文所述錨桿錨固質量等級快速評級方法,通過對原始錨桿數據進行歸一化以及進行x 方向修正等預處理操作,得到可供分類的中間數據,然后計算其峰值均值以及相應的斜率絕對值等定量分類標準,從而實現對錨桿錨固質量等級的快速評級。
與目前主流的錨桿錨固質量等級評級方法相比,本文所述方法的優勢有以下幾個方面:
(1)簡單易懂,本文所述方法基于統計結果得到可用來進行分類的閾值,基于閾值進行錨桿錨固質量等級快速評級;
(2)計算量小,僅針對錨桿的桿底反射的時域信號進行處理,能快速得到分類結果;
(3)準確高效,應用該方法得到的分類結果與原人工首次分類的結果存在不一致時,由于人工判定結果具有隨意性,人工再次確認基本都能認可本算法分類所得到的結果,表明本算法具有較好的準確性。

