平面載荷作用下四邊簡支層合平板屈曲的有限元模擬

陸旭生

（廣東省輕紡建筑設計院有限公司 廣東廣州 510080）

1 概述

隨著建筑業的發展，復合材料憑借其輕質、高強、耐腐蝕和耐老化，在建筑裝飾工程中的運用越來越多。由于其一般較薄，在較小的荷載作用下發生屈曲的問題也比較突出。本文研究的層合平板是各種復合材料層合板中最簡單又應用最廣的一種，以經典層合板理論為基礎，而不考慮層間應力和橫向剪切影響。

在復合材料結構分析中，已經廣泛采用有限元數值仿真分析，本文計算分析采用ANSYS軟件，選用Shell99（線性層合結構殼單元）。ANSYS先定義材料性質、鋪層角、鋪層厚度，然后通過由下到上的順序逐層疊加組合為復合材料層合結構。假設屈曲以前是薄膜應力狀態，不考慮拉彎耦合影響，當平板受平面載荷時，由薄膜狀態進入屈曲狀態，求引起屈曲的最小載荷。

2 參數設置與模型建立

選取某一復合材料板材，矩形、四邊簡支，沿著x方向作用均勻平面力x。

圖1 均布單向平面壓力下的簡支矩形層合板

某復合材料板寬b=1m，單層厚度5mm；彈性模量Ex=25MPa，Ey=Ez=1MPa；剪切模量 Gxy=Gxz=0.5MPa，Gyz=0.2MPa；泊松比 νxy=νxz=0.01，νyz=0.25；取平面壓力x=1N。

模擬以上材料屬性的四邊簡支層合平板在平面荷載作用下的屈曲，分別建模特殊正交各向異性層合板、對稱角鋪設層合板、反對稱正交鋪設層合板、反對稱角鋪設層合板，考慮鋪設層數、長寬比和鋪設角這些參數的影響。[1]

3 分析結果

3.1 特殊正交各向異性層合板

分析不同層數和不同長寬比時的屈曲，見表1。

（1）x向半波數=1、y向半波數=1時：

（2）與表1計算結果類似，x向半波數=2、y向半波數=1時，以及x向半波數=3、y向半波數=1時：隨著層合板層數的增加，屈曲荷載增大，層數越多，屈曲載荷大小增大越明顯；在層數一定時，長寬比a/b對屈曲載荷大小在比值較小時影響明顯，并且隨著比值增大，屈曲載荷逐漸減小。[2]

表1 不同層數和長寬比時的特征值

（3）分析在層合板層數一定時，不同長寬比a/b下屈曲時特征值的變化情況，對計算數據在相同層數時的特征值結果進行分析。相同層數下，不同長寬比a/b時的特征值大小變化如圖2所示。

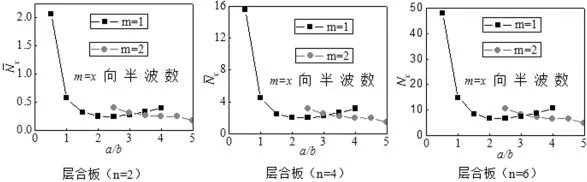
圖 2-a/b 關系

3.2 對稱角鋪設層合板

分析不同層數和不同鋪設角時的屈曲，鋪設情況如圖3所示。

圖3 對稱角鋪設層合板

在對稱角鋪設層合板鋪設角度相同時，隨著層合板層數的增加，屈曲荷載增大，層數越多，屈曲載荷大小增大越明顯；在層數一定時，鋪設角度?對屈曲載荷大小有明顯影響，并且隨著鋪設角度?增大，屈曲載荷先減小，在鋪設角度45°左右達到最大值，隨著鋪設角度?的進一步增大，屈曲載荷開始減小。[3]

3.3 反對稱正交鋪設層合板

分析不同層數和不同長寬比時的屈曲，鋪設情況如圖4所示。

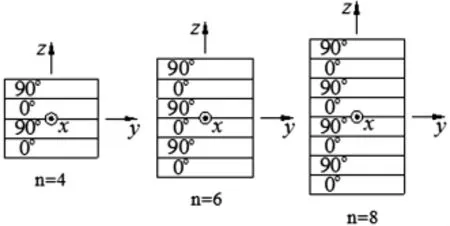
圖4 反對稱正交鋪設層合板

計算結果：

表2 不同層數和長寬比的特征值

在反對稱正交鋪設層合板的長寬比a/b相同時，隨著層合板層數的增加，屈曲荷載增大，層數越多，屈曲載荷大小增大越明顯；在層數一定時，長寬比a/b對屈曲載荷大小在比值小于1時影響明顯；大于1后，隨著比值增大，屈曲載荷呈微小的波動形變化。[4]

3.4 反對稱角鋪設層合板

分析不同層數和不同角度時的屈曲，鋪設情況如圖5所示。

與對稱角鋪設層合板的情況類似，在反對稱角鋪設層合板鋪設角度相同時，隨著層合板層數的增加，屈曲荷載增大，層數越多，屈曲載荷大小增大越明顯；在層數一定時，鋪設角度?對屈曲載荷Nˉx大小有明顯影響，并且隨著鋪設角度?增大，屈曲載荷先減小，在鋪設角度45°左右達到最大值，隨著鋪設角度?的進一步增大，屈曲載荷開始減小。[5]

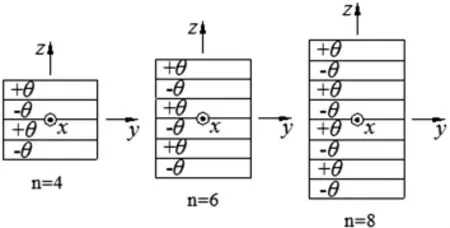
圖5 反對稱角鋪設層合板

4 結語

（1）文中運用有限元軟件模擬了特殊正交各向異性層合板、對稱角鋪設層合板、反對稱正交鋪設層合板和反對稱角鋪設層合板的屈曲，研究在不同鋪設層數、不同長寬比和不同鋪設角情況下屈曲載荷的變化，分析屈曲載荷的變化規律。總結鋪設層數、長寬比和鋪設角這些參數的影響，為復合材料層合板的材料設計提供一些有益參考。

（2）本文研究的是比較簡單的層合平板，并且考慮的參數比較有限，存在一定的不足。在以后的分析中可以考慮更多參數、更加復雜的約束、更復雜的形狀；以及可以考慮更復雜的鋪設情況、復雜載荷的影響；在材料參數方面，可以考慮彈性模量、剪切模量，甚至泊松比的變化對屈曲的影響。