表層相關多次波壓制算法在CMP道集中的應用

劉仕友， 馬繼濤，孫萬元

(1. 中海石油(中國)有限公司 湛江分公司，湛江 524057；2. 中國石油大學(北京) 地球物理學院，北京 102249)

0 引言

海洋地震勘探中，由于海水表面及海底處的波阻抗差值大，導致海水表面和海底的反射系數較高，從而使得海洋地震數據中存在非常嚴重的多次波問題。多次波的存在干擾了對有效波地識別，導致速度分析、疊前和疊后偏移的不準確，影響地震成像的真實性和可靠性，對地震解釋工作也帶來了很大地干擾,有效壓制多次波對復雜油氣藏區域地震數據的處理和解釋有重要的意義。

海洋地震勘探中，海洋自由表面的強反射作用使得地震數據中表層相關的多次波能量占絕大部分，因此，針對海洋地震數據的表層相關多次波壓制方法研究是多次波壓制的主流,多次波的壓制方法可以分為兩大類[1]:

1)信號處理方法，是基于有效波和多次波之間不同的某種特性(如周期性和可分離性)。基于多次波和有效波之間的差異，可以設計一個濾波器對其進行濾除，因此這類方法統稱為濾波法。但這類方法都是有一定的假設的，如“周期性”假設多次波具有周期性而沒有有效波，“可分離性”假設通過一些變換可以將多次波和有效波分離開，進而通過切除的方式壓制多次波。比較典型的濾波方法有預測反褶積(周期性)，FK濾波(可分離性)，共中心點疊加(可分離性)，拋物線Radon變換(可分離性)等。濾波法在地下構造比較簡單的情況下是有效的，但復雜區域的地震數據有可能無法滿足濾波法的假設(隨著偏移距的增加，多次波不再具有周期性)；多次波和有效波在變換域的差異越來越小。在這些情況下進行多次波壓制有可能出現壓制不完全，或者損傷有效波能量的情況。

2)基于波動理論。該類方法以表層相關多次波衰減，即SRME最為知名。該方法由Berkhout[2]提出，他針對表層相關多次波和層間多次波，在考慮反子波的情況下，加入炮點和檢波點性質算子的作用，利用多維反演算法初步提出了多次波壓制的反饋迭代模型。Verschuur等[3-5]基于Berkhout的理論，采用數據驅動的方式，利用地震數據自身在時空域的二維褶積實現多次波的預測，之后利用自適應相減的手段將預測的多次波和數據中的多次波進行匹配相減，以期達到多次波壓制的目的。該類方法不需要地下介質的任何信息，一經提出就引起了廣大地球物理學者的興趣，目前已經成為海洋地震數據表層相關多次波壓制最為常用的算法之一。除此之外，Weglein[6]、Faqi Liu[7]等分別基于逆散射級數序列、恒定內插理論推導出了類似的多次波預測相減方法。

常規的SRME是一種基于波動理論的算法，該算法要求地震數據是全波場規則的地震數據，即地震數據由零偏移距至最大偏移距都要有等間距的數據覆蓋，且炮點間隔和檢波點間隔相等。實際數據無法滿足方法要求，因此在利用SRME算法進行實際數據處理之前，或處理數據的同時，需要對數據進行規則化和插值外推處理。如果僅僅是二維地震數據，插值外推和規則化的運算量還可以接受，但若是三維地震數據，由于橫測線方向數據極為稀疏，通過三維規則化處理得到地震數據存在著運算量巨大和數據質量不可靠等問題。Verschuur[3]和Kelamis等[8-9]提出了在地下介質橫向起伏變化不大時，在CMP道集中應用SRME進行多次波壓制的方法，該方法可以在一定程度上避免由于數據不規則和采樣稀疏等帶來的問題。

筆者對SRME應用在CMP道集中的算法進行討論，該算法是一種表層相關多次波壓制的高效算法，假設地下介質或者局部為一維介質，這樣數據中的每個CMP道集可以視為一維介質情況下采集到的炮記錄。對于真正的一維介質而言，采集到的所有炮記錄都是相同的，因此CMP道集的SRME算法可以通過在頻率波數域的簡單向量相乘，而不是矩陣相乘的形式實現，這樣可以大大減小算法對內存的需求，降低算法的復雜度，提高計算效率。

1 方法原理

首先從表層相關多次波壓制的基本算法-反饋迭代理論闡述方法的原理。該理論認為，如果沒有自由表層的反饋效應，地表接收到的地震數據P0(z0)可以表示為：

P0(z0)=D(z0)X0(z0，z0)S(z0)

(1)

其中：z0為震源和檢波器的垂向位置坐標；S(z0)為震源函數；D(z0)為檢波點性質矩陣；X0(z0,z0)為有效波反射矩陣。

若式(1)中加入自由表層的反饋效應，則接收到的地震數據可以表示為：

P(z0)=P0(z0)+[P0(z0)A(ω)]P0(z0)+

[P0(z0)A(ω)]2P0(z0)+…

(2)

(3)

稱其為表層算子。

由式(2)可以推導出有效波波場(含層間多次波)，即表層相關多次波壓制的表達式：

P0(z0)=P(z0)-A(ω)P2(z0)+

A2(ω)P3(z0)-A3(ω)P4(z0)+…

(4)

如果地下介質是一維的，采集到的炮記錄都是相同的，則表層相關多次波壓制可以利用式(5)進行。

P0(kx,ω;z0)=P(kx,ω;z0)-

A(ω)P2(kx,ω;z0)+

A2(ω)P3(kx,ω;z0)-

A3(ω)P4(kx,ω;z0)+…

(5)

其中:kx、ω分別為波數和頻率；P0(kx,ω;z0)是炮記錄對應的單頻切片，在一維情況下，因為所有的炮記錄都是相同的，所以P0(kx,ω;z0)對應的是P(z0)矩陣的一列。式(4)中的矩陣相乘可以由式(5)中的向量相乘代替。

在實際情況下，地下介質并不完全滿足一維的假設，所有的炮記錄不是完全相同的，但是如果用CMP道集代替炮記錄，會更好地滿足一維介質的假設。在產生多次波的地層，即介質上部構造起伏較為平緩的情況下，CMP道集的多次波壓制可以取得很好的結果。

需要注意的是，在CMP道集進行表層相關多次波壓制的步驟和炮集預測類似，都要進行數據的插值外推的處理，即如果CMP道集最小偏移距不為零，需要利用一定的方法對缺失的數據進行插值外推處理。在動校正后的道集進行插值，之后再反動校正，一般就能滿足方法的需求。如果CMP道集的地震道個數太少，可以將相鄰的幾個CMP道集合并起來，形成CMP超道集，對該超道集進行規則化、插值和多次波預測處理。將CMP道集的多次波預測出來之后，用炮集的SRME方法類似，需要用自適應相減的方法將預測的多次波從原始數據中減去。

因此，利用本文方法進行表層相關多次波壓制的步驟如下：

1)讀取地震數據D，得到CMP道集的偏移距信息，如地震數據近偏移距不為零，則利用拋物線Radon變換對數據進行近炮檢距外推處理，得到數據Dexp。

2)對步驟1)得到的CMP道集Dexp，沿時間和偏移距方向做傅里葉變換，得到頻率-波數域的地震數據Dexp_fk。

3)對步驟2)得到的頻率-波數域地震數據進行向量相乘運算，得到頻率-波數域的多次波記錄Mexp_fk。

4)對步驟3)得到的頻率波數域多次波記錄Mexp_fk進行反傅里葉變換，得到時間-空間域的多次波記錄Mexp；若數據進行過外推處理，則將外推的地震道記錄進行剔除，得到對應的多次波記錄M。

基于最小能量準則，將D和M進行自適應相減，得到多次波壓制后的結果P。

2 數據示例

我們分別用一個平層速度模型、一個橫向平緩起伏的速度模型生成的模擬地震數據和一個實際海洋數據,對方法的可行性和有效性進行了驗證。

2.1 模擬數據算例

第一個模型是平層速度模型，如圖1所示。

圖1 平層速度模型Fig.1 Flat layer model

在圖1中從2 000 m至8 000 m，每隔20 m放置一個震源，并在震源左側放置101個檢波器接收，模擬出201個炮記錄。對模擬出的共炮點道集，根據數據震源和檢波點坐標計算出每道的CMP數值，并抽取數據共CMP道集。在此只展示其中的3個CMP道集，因為此數據為平層速度模型數據，因此3個CMP道集都是相同的(圖2)。

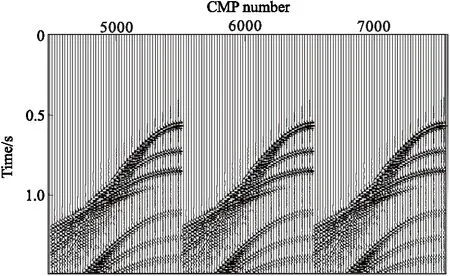
圖2 平層數據所對應的3個CMP道集Fig.2 The 3 CMP gathers corresponding to the flat layer data

為了對比常規SRME方法和CMP道集多次波預測方法的方法原理，在此給出了常規SRME方法和本文方法的數據矩陣，分別為頻率-空間域和頻率-波數域的數據矩陣，如圖3所示。

由圖3可以看出，常規SRME方法的數據矩陣，每一列對應的為一個共炮點道集，其元素都是相同的；而頻率波數域的數據矩陣，其能量幾乎都聚焦在了反對角線上，因此數據矩陣的相乘可以用反對角線方向對應元素的點乘代替，可以大大減小計算量。

圖3 數據矩陣Fig.3 Data matrices(a)平層數據常規SRME方法數據矩陣；(b)對應的頻率-波數域數據矩陣

圖4 平層數據CMP道集所對應的多次波結果Fig.4 The multiple result corresponding to the CMP gathers of flat layer data

圖5 平層數據多次波壓制后的CMP道集Fig.5 The CMP gathers after multiple attenuation of the flat layer data

圖6 共偏移距道集Fig.6 Common offset gather(a)多次波壓制前;(b)多次波壓制后

遵循CMP道集多次波預測的方法步驟，對每個CMP道集做二維傅里葉變換，并對變換后的頻率-波數域數據進行向量點乘運算，得到該CMP道集對應的多次波。圖4展示的是圖2的三個CMP道集所對應的三個多次波記錄，由圖4可以看出，預測的多次波結果與原數據中的多次波在旅行時和同相軸形態上都較為吻合。將預測出的多次波從原數據中自適應減去，得到圖5即多次波壓制后的結果。

多次波壓制前后的共偏移距剖面如圖6所示，可以看出，對于平層數據，由于所有位置處的CMP道集都是相同的，利用本文方法進行多次波預測和壓制，和常規SRME方法進行多次波壓制的效果是一樣的。

利用橫向平緩起伏變化的速度模型(圖7)正演模擬出的共炮點道集，抽取其CMP道集(圖8)進行多次波預測的工作。同樣給出了常規SRME方法頻率-空間域數據矩陣和本文方法的頻率-波數域數據矩陣(圖9)。在圖9中可以看出，由于此數據橫向有了起伏變化，每一列元素所對應的共炮點道集也有了些微的變化，但頻率-波數域的數據矩陣能量仍然集中在反對角線元素上，因此可以同樣利用向量的點乘運算預測出數據的多次波。

圖7 一個橫向平緩起伏的速度模型Fig.7 A horizontal gentle varying velocity model

圖8 橫向平緩起伏數據的三個CMP道集Fig.8 3 CMP gathers of the horizontal gentle varying velocity model

圖9 橫向平緩起伏數據的數據矩陣Fig.9 The data matrix of the horizontal gently varying model(a)頻率-空間數據矩陣；(b)頻率-波數數據矩陣

圖10 起伏數據預測的多次波Fig.10 Predicted multiple of the horizontal gently varying model

圖11 自適應相減之后的結果Fig.11 The result after adaptive subtraction

圖12 橫向平緩起伏數據共偏移距剖面Fig.12 Common offset gather of the horizontal gently varying model(a)多次波壓制前；(b)多次波壓制后

對圖8中的CMP道集沿時間和空間方向分別進行傅里葉變換，得到頻率-波數域的CMP道集，并將其進行點乘運算，得到頻率-波數域的多次波，之后對其進行反傅里葉變換，得到時間-空間域的多次波(圖10)；將預測得到的多次波從原數據中自適應減去，得到多次波壓制后的結果(圖11)。從圖11中可以看出，單個CMP道集的多次波壓制可以取得較好的效果，但在遠偏移距處，由于地形起伏使得預測的多次波帶有一定的誤差，從而導致多次波壓制有一定的殘余，此數據所對應的多次波壓制前后的共偏移距剖面如圖12所示。從圖12中也可以看出，除了在地形起伏變化較為劇烈的個別區域之外，對該數據進行多次波壓制也可以取得較好的效果。

圖13 實際數據的CMP道集Fig.13 CMP gathers of real data(a)原數據；(b)預測的多次波；(c)自適應相減之后的結果

圖14 實際數據數據矩陣Fig.14 Data matrix of real data(a)頻率-空間數據矩陣；(b) 頻率-波數域數據矩陣

2.2 實際數據算例

利用墨西哥灣的一個實際數據對方法進行了進一步驗證。圖13(a)給出的是墨西哥灣數據的一個CMP道集，該CMP道集的近偏移距為﹣100 m，首先利用拋物線Radon變換對該數據的近偏移距進行了插值外推處理，之后對插值外推的數據沿空間和時間進行傅里葉變換，之后對該頻率-波數域數據進行點乘并做反傅里葉變換，得到該CMP道集對應的多次波(圖13(b))，將該多次波從原CMP道集中自適應減去，得到多次波壓制后的結果(圖13(c))，可以看出對于實際數據，本文方法仍然可以取得較好的效果。

從圖14中可以看出，即使本實際數據比較復雜，其頻率-波數域數據矩陣的能量仍然大部分聚焦在了反對角線附近。因此利用兩次傅里葉變換之后數據的點乘運算進行多次波預測對于實際數據仍然是有一定的意義的。

圖15為實際數據對應的共偏移距剖面，圖16為地形起伏區域及中部平緩區域多次波壓制后剖面的局部放大圖。從圖15和圖16中可以明顯看出，除了在地形起伏變化較大，不滿足本方法假設的區域(箭頭所指)，本文方法均能夠較好地預測并壓制多次波。

圖15 實際數據共偏移距剖面Fig.15 Common offset gather of real data(a)多次波壓制前；(b)多次波壓制后

圖16 多次波壓制后共偏移距剖面的局部放大圖Fig.16 The enlarged figure of common offset profile after multiple attenuation(a)左側起伏區域；(b)中部平緩區域；(c)右側起伏區域

3 結論

筆者討論了一種SRME在CMP道集應用的簡化形式，該方法簡單快捷有效，具有較好的操作性和應用性；利用兩個模擬數據和一個海洋實際數據驗證了方法的可行性與有效性。綜上所述，可以得出以下幾點結論和建議：

1)該方法可在地下地層較為均勻、起伏不大時使用，計算結果具有一定的精度，可以作為中間查看結果的一個工具使用。

2)該方法同樣要求數據是全波場數據，即近偏移距如果有數據缺失，必須做插值外推處理。

3)若CMP道集道數偏少，可以將附近幾個CMP道集聯合起來組成超道集進行多次波地壓制。

4)對于三維地震數據，在地下地層起伏不大時，也可將此算法應用在三維地震數據的CMP道集中，相對于常規的全三維算法，本文算法更加簡單，計算效率高，而且能夠達到一定的多次波壓制效果。