無砟軌道—路基結構相似模擬試驗研究

趙如鋒，趙國堂，楊 斌，趙 磊

（1.北京交通大學 土木建筑工程學院,北京 100044；2.中國國家鐵路集團有限公司,北京 100844；3.中國鐵道科學研究院集團有限公司 鐵道建筑研究所,北京 100081）

隨著高速鐵路的大量建設,各種不良地質環境引起的軌道問題也逐步顯露。當無砟軌道鋪設于基礎穩定性較為薄弱的區域,如差異沉降區、膨脹土、路基凍脹變形量較大等區域［1］,基礎變形將直接影響軌道平順性以及無砟軌道受力,較為劇烈的差異沉降會導致層間動態離縫和脫空,影響行車舒適性和安全性。路基變形影響研究成為高速鐵路路基上無砟軌道研究的難點問題。

對于軌道—路基模型試驗而言,軌道結構對路基變形響應的理論研究進展相當有限。陳兆瑋,孫宇,翟婉明等［2］通過解析方法分析了雙塊式無砟軌道、CRTSⅡ型板式無砟軌道橋梁墩臺變形與軌面不平順之間的映射關系；蔡小培、趙立寧等［3］研究了地面沉降引起的路基上單元板式和雙塊式無砟軌道軌面變形問題,對比了幾種常見地面沉降對無砟軌道結構平順性的影響；陳鵬、高亮等［4］針對地面沉降開展無砟軌道結構平順性研究,分析了不同形式地面沉降引起的軌道結構變形。趙磊［5］分析了過渡段路基上拱對大單元雙塊式無砟軌道受力及行車動力影響。可以看出,基礎變形對無砟軌道影響的分析多停留在理論分析層面,側重點多針對軌面平順性及行車動力響應,而針對基礎變形在路基內部傳遞規律及其對無砟軌道受力影響方面的理論研究不足,基礎變形對無砟軌道影響的試驗研究尚屬空白。

高速鐵路路基土體的受力復雜,變形傳遞過程也并非既有的彈性模型或塑性、彈塑性模型能夠真實模擬,加上無砟軌道層間相互作用關系也極為復雜,目前尚缺乏合理的模型能夠對無砟軌道層間相互作用關系進行真實模擬。

要掌握基礎變形對無砟軌道軌面平順性及軌道受力的影響過程,必須首先掌握現場條件下基礎變形傳遞至路基表面、無砟軌道及軌面的實際變形傳遞過程,并對基礎變形過程中無砟軌道各層的荷載效應及離縫特征進行監測。相似模擬試驗在采礦工程［6-8］、隧道工程［9-11］、路基工程［12-16］均有大量應用,為獲取真實結構在荷載下的響應提供了有價值的參考。然而,相似模擬試驗在無砟軌道方面尤其是基礎變形對無砟軌道影響研究方面尚無應用。

本文在無砟軌道—基礎變形仿真分析的基礎上,采用量綱分析法,進行建立包含下部基礎的無砟軌道相似試驗仿真模型研究。

1 相似模型設計準則

當所研究問題的參數較多且相互關系復雜,無法得出各參數間的解析關系時,可采用量綱分析法確定相似準則和相似指標。

量綱分析法是用量綱方程表示物理方程,根據量綱方程等號兩邊量綱齊次性,解出物理方程式中各物理量的未知冪指數。本相似試驗模型中所包含的物理量有：

（1）結構幾何尺寸l；

（2）結構上荷載,包括自重（用重度γ表示）和位移荷載Fy；

（3）結構反應,包括撓度δ、應力σ和應變ε；

（4）材料性能,包括彈性模量E和泊松比ν,扣件剛度k。

假定上述9個物理量之間存在的函數關系為

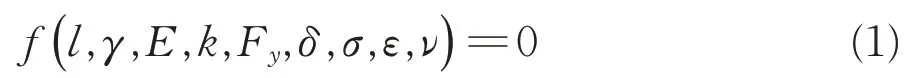
選定力量綱［F］,長度量綱［L］作為基本量綱,上述9個物理量與其對應的量綱關系見表1。

表1 各物理量與基本量綱的關系

選取γ和E組成基本量群,令式（1）中其他量綱與此基本量群的量綱相除,得到

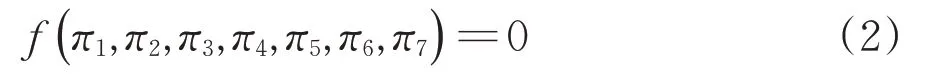
式中：π1—π7均為無量綱量。

以π1為例說明其求解,

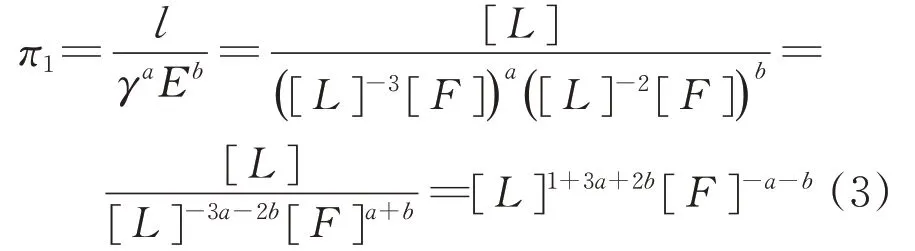
為使π1為無量綱量,則式中未知量a和b需滿足

由式（4）可得a=－1,b=1,代入式（3）可得到

同理可得到π2—π7表達式,匯總得相似判據

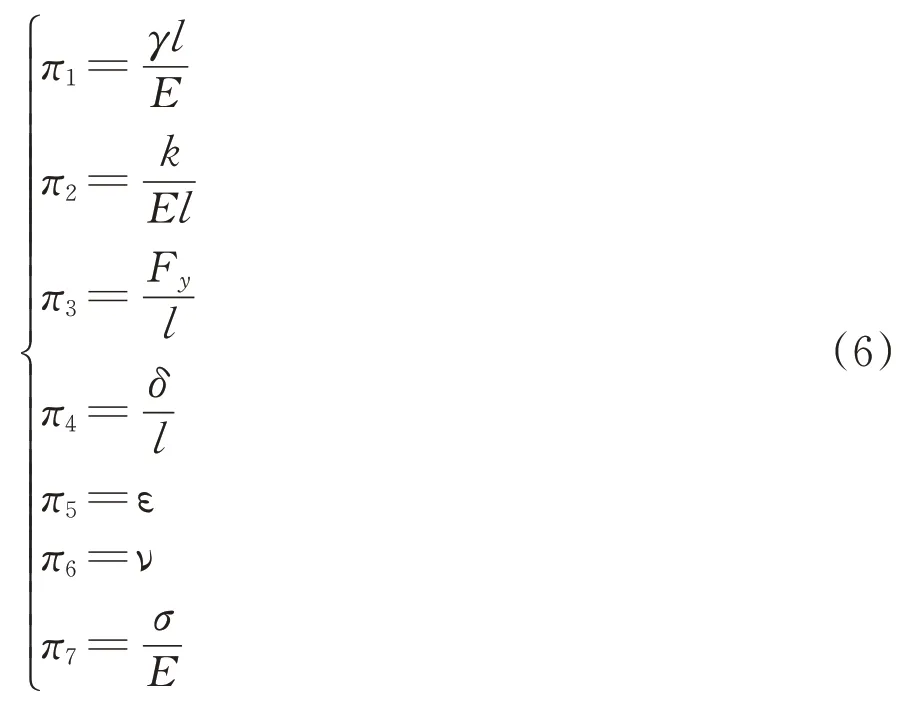
因此,在模型設計中若能滿足式（7）中條件,則模型滿足量綱相似。

式中：m表示模型；p表示原型。

根據量綱相似設計原則,當原型與模型尺寸比例為1：n時,若材料彈性模量比例1：n、加載位移比例為1：n、重度γ 比例為1：1、扣件剛度1：n2時,滿足量綱相似,此時結構變形比例為1：n,應力比例為1：n；若材料彈性模量1：1,加載位移比例為1：n,重度γ比例為n：1時,亦滿足量綱相似,此時結構變形比例為1：n,應力比例為1：1。

2 相似模型的驗證

依據上述相似模型設計原則分別建立不同比例參數的無砟軌道—路基變形仿真分析模型,對所獲取的相似模型設計原則進行驗證。模型自上而下包含鋼軌、扣件、軌道板、自密實混凝土、底座板、基床以及地基,共建立如下4個模型。

模型1：無砟軌道—路基實尺分析模型。

模型2：無砟軌道—路基直接縮尺模型（僅尺寸縮放的非相似模型）。

模型3：無砟軌道—路基尺寸1：4 相似分析模型,彈性模量比例1：4（通過彈模比例達到模型相似）。

模型4：無砟軌道—路基1：4 比例分析模型,材料重度比例4：1（通過重度比例達到模型相似）。

建立的CRTSⅢ型板式無砟軌道及下部路基模型如圖1所示。建立的4 個對比模型參數見表2和表3。實尺模型總長85.3 m,加載波長20 m,最大加載量40 mm；比例模型總長21.3 m,加載波長5 m,最大加載量10 mm。

利用仿真分析軟件對原型、直接縮尺模型、2種相似模型的荷載響應進行靜力分析。在模型2、模型3、模型4 中,對地基底面施加5 m（1：4）波長的沉降變形,將計算結果中尺寸與位移放大4 倍,應力比例尺仍為1：1,與模型1 進行對比,結果如圖2—圖6所示。

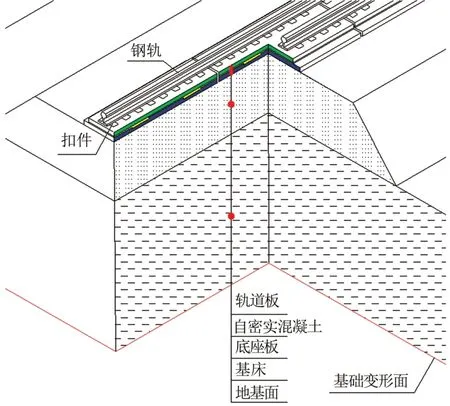
圖1 CRTSⅢ型板式無砟軌道及下部路基模型

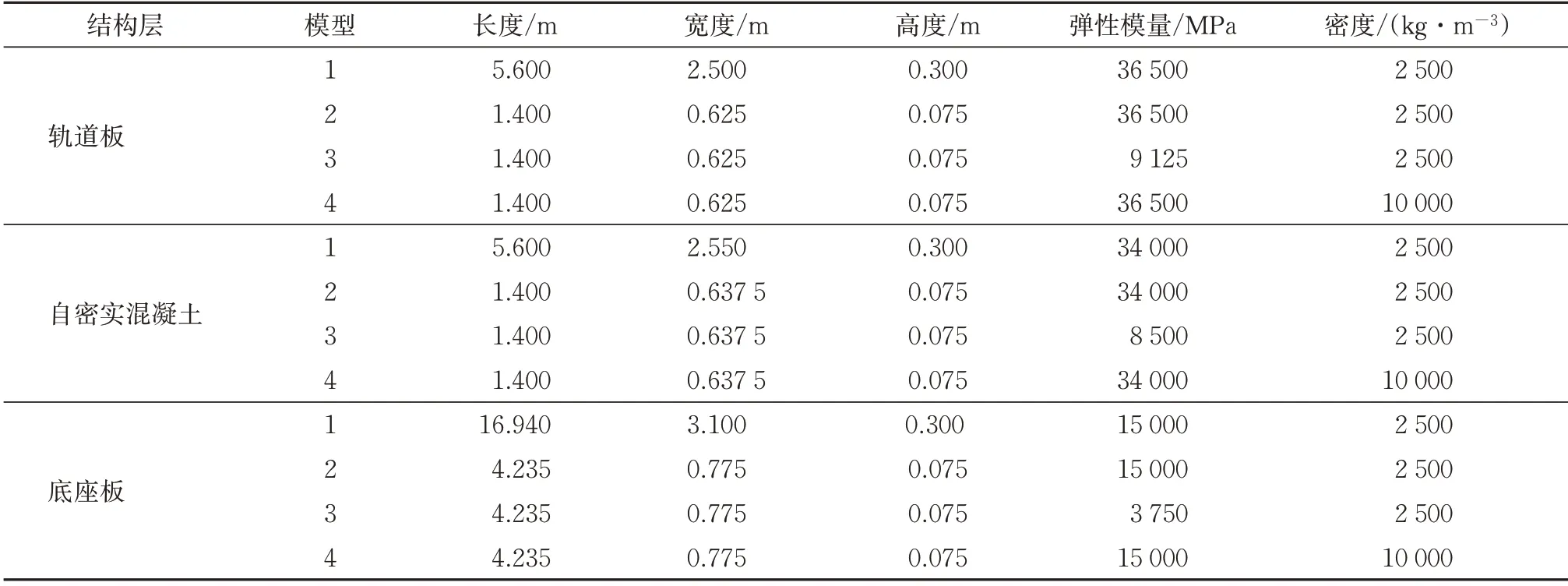
表2 無砟軌道結構參數

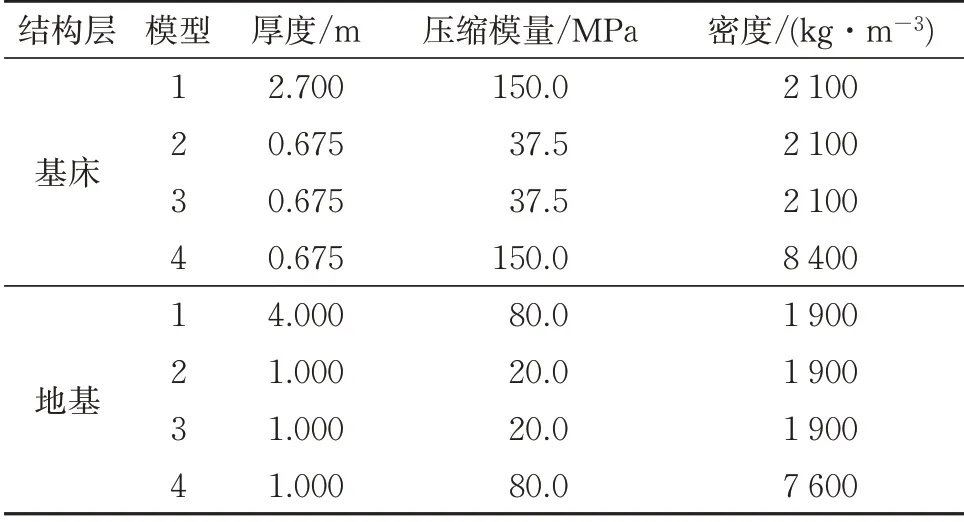
表3 下部基礎結構參數

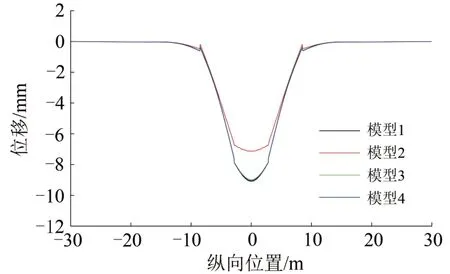
圖2 軌道板豎向位移

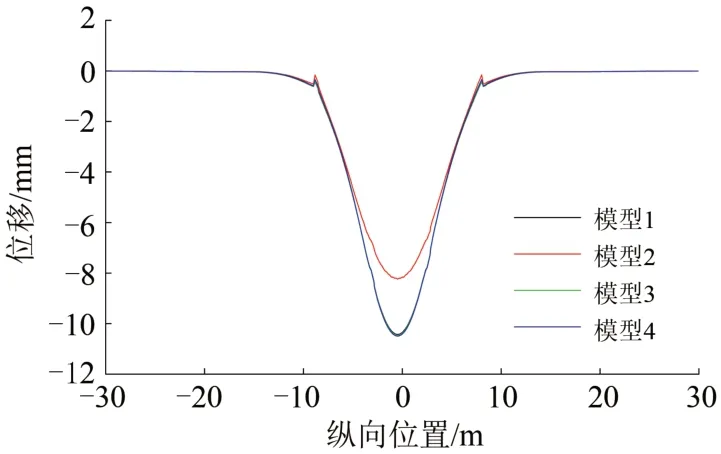
圖3 底座板豎向位移

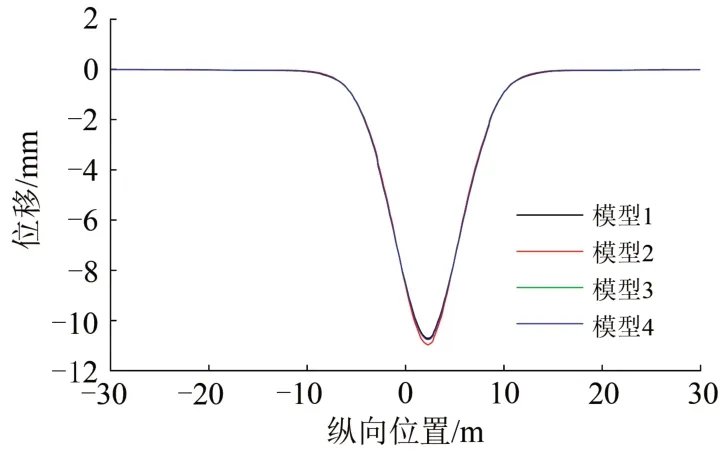
圖4 基床表層豎向位移

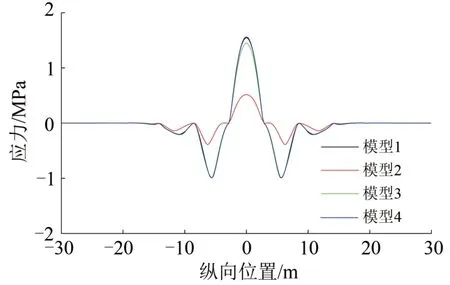
圖5 軌道板表面縱向應力

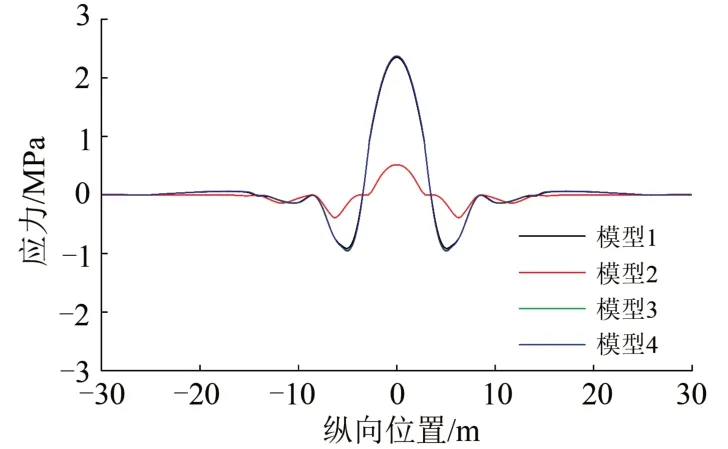
圖6 底座板表面縱向應力

通過4 種模型荷載響應對比分析可以得出,采用直接縮尺模型時,基礎變形曲線吻合較好,但軌道板及底座板變形與實尺模型間差異較大,軌道板及底座應力分布也與實尺模型差異較大。當改變結構中材料彈性模量的比例或材料重度的比例達到模型相似時,基礎變形所產生的無砟軌道變形及應力與實尺模型基本等比例相近。由此驗證了基于量綱相似模型設計準則的準確性。

3 相似模型試驗設計

3.1 相似材料比選

相似材料的選擇是本試驗方案中的難點,方案中涉及的主要材料有路基土體和混凝土材料2種。

對于路基土體,根據調研可知,在利用離心機進行相似模型設計時,西南交大羅強教授團隊［15］做了部分簡化,認為路堤部分為連續均勻、各向同性體,路堤各層采用Mohr-Coulomb 材料模擬,試驗采用級配砂作為路基填料,粉體顆粒直徑d50為0.4 mm、細粒含量3.9%、不均勻系數Cu為5、曲率系數Cc為1.25,屬于級配良好的中砂。級配砂按照相似比例關系換算成原型填料屬于級配良好的A 組粗顆粒土填料。模型的壓實系數為0.95。武漢理工大學芮瑞副教授團隊［16］采用內摩擦角31°,顆粒相對密度2.67 g·cm-3的干凈河砂作為填料進行試驗,利用填料質量控制砂的密度,將其密度控制在1.688 g·cm-3。每填砂15 kg,均勻虛鋪后用夯板夯至厚度25 mm。

可以看出,既有相似模型構建時多采用砂模擬土體,為本文土體的相似材料選擇提供了參考和依據。為模擬深層壓縮模量較大的土體以及淺層壓縮模量較小的土體,本文分別采用細砂和中砂對深層和淺層地基進行模擬。

對于混凝土材料,國內外在開展模擬試驗時多采用與模擬對象材料一致的混凝土材料開展縮尺試驗,主要原因是此類試驗研究對象主要為混凝土材料本身的極限力學性能。本次試驗對混凝土極限力學性能無要求,假定混凝土材料均為各向同性線彈性材料,選用相似材料的原則為材料彈性模量1：4,重度1：1。目前文獻中主要選用的材料有：低彈模金屬、有機玻璃、環氧樹脂、石膏、水泥砂漿、微粒混凝土、環氧微粒混凝土等。上述材料基本可以滿足不同相似比時混凝土材料的模擬應用。經比選,適合應用于此模型的是低彈模砂漿。無砟軌道板為C55混凝土,底座板為C30混凝土,彈性模量分別為36.5 GPa 和31 GPa,相似材料要達到的彈性模量在7～9 GPa之間。

本文選用了1 種摻膨潤土水泥砂漿進行模擬。摻膨潤土的砂漿彈性模量低,極限變形大,能適應較大變形。根據應用經驗,分別使用了3種配方的膨潤土砂漿進行比對和測試,具體配比見表4。

3種方案制作出的砂漿如圖7所示。

從和易性角度來看,較小的水灰比差異,也會引起摻膨潤土砂漿明顯的黏稠度差異,其中,方案A的流動性最大,并且表層伴有輕微泌水現象,方案C 砂漿流動性較差,振搗后可滿足密實度要求。方案B的和易性最好。

對砂漿彈性模量進行測試,結果如圖8所示,由圖8可見,3種方案砂漿7—28 d彈性模量均位于7～8 GPa,均滿足試驗需求,綜合考慮砂漿和易性和彈性模量,本試驗選用方案B來進行模擬。試驗期為澆筑完成后15 d左右,對應彈性模量為7.5～8 GPa之間。

表4 3種配方膨潤土砂漿配比

圖7 3種方案制作的砂漿

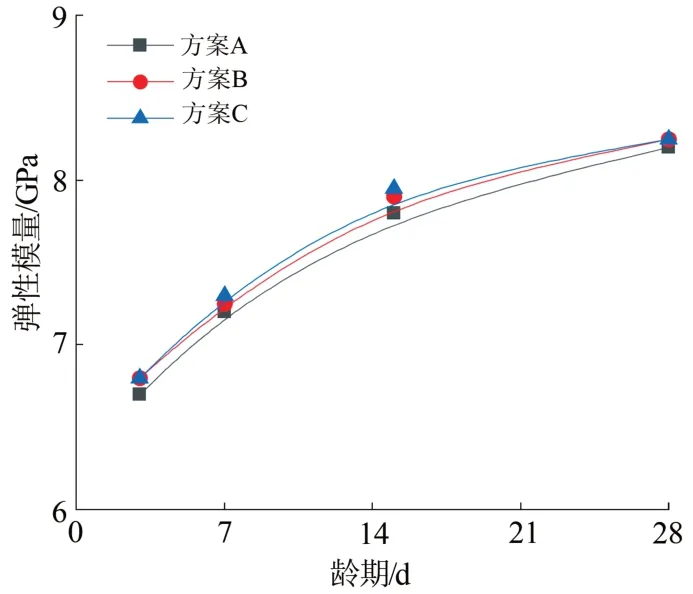
圖8 3種方案不同齡期彈性模量檢測結果

3.2 試驗平臺設計

為獲取下部基礎不均勻沉降變形后軌道結構平順性變化規律及結構受力變化規律,需設計包含軌道、路基、地基且能夠模擬下部基礎不均勻沉降變形的試驗平臺,所模擬的不均勻沉降變形能夠涵蓋多個變形波長及變形量。為此,本文設計方案中試驗平臺自下而上依次為軌道、路基、節段變形板、調整裝置、試驗臺座。四周采用擋板進行圍擋,為降低路基與圍擋之間的邊界效應的影響,在側邊位置處設置了滑動層,以達到對稱邊界的效果,如圖9所示。

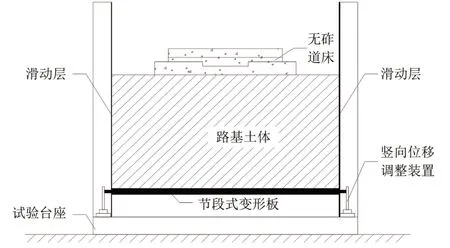
圖9 試驗臺整體方案斷面圖

為方便基礎變形的觀測,試驗臺座設計成兩端頭為擋墻,側邊為立柱的方案,立柱內側設置擋板進行圍擋。其中一側擋板為鋼板,另一側為透明有機玻璃（亞克力板）,如圖10所示。

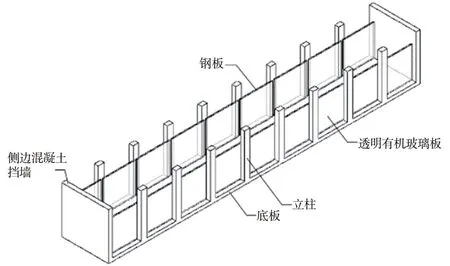
圖10 試驗臺座方案圖

3.3 加載方式

節段變形板是實現基礎底部變形的關鍵部件。為了實現不同的沉降波長,需要根據試驗需求設計不同長度的變形板,變形板四角可實現上下位移以模擬基礎不同的變形量。

本文中,節段變形板采用混凝土板模擬,利用不同長度的混凝土板的折線（如圖11）變形模擬真實沉降中的曲線。

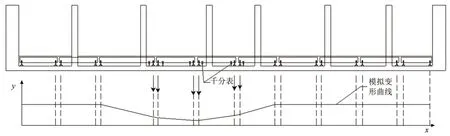
圖11 沉降曲線模擬過程

在變形板的端部,設置了軌道板用精調爪,如圖12所示,在安裝時對變形板進行精調,在試驗時實現豎向調整功能。單個精調爪的承載量為6 t,豎向調整范圍為0～85 mm,在設置變形板豎向位置時,將精調爪的豎向初始位置設置至立柱中部,實現精調爪±40 mm的變形量。

圖12 變形板端部精調爪

在進行試驗時,每個精調爪位置處均設置1個千分表,如圖13所示。以掌握實際試驗變形的加載量。

實際加載過程控制表明,精調爪調整過程中,可以將千分表精度控制至0.2 mm 以內,滿足測試需求。

3.4 模擬波長及幅值

圖13 沉降控制用千分表

本文中,由于采用節段變形板的板端位移所產生的折線模擬沉降、上拱變形曲線,因此,單個沉降、上拱變形曲線最少由2 塊變形板實現。考慮CRTSⅢ型板式無砟軌道的軌道板長度,本次模擬試驗中選取的波長為板長的倍數,即最小模擬波長為5.6 m,對應變形板最小長度選為5.6 m/4/2=0.7 m。

同時,為盡可能減少變形板的數量,選擇在一側布置0.7 m 長的變形板,另外一側均布置2×0.7 m=1.4 m 長的變形板,短波長的沉降、上拱變形均在短的變形板一側實現。變形板的大致布置如圖14所示。

圖14 變形板間隔布置圖（單位：mm）

當模擬基礎變形（含上拱與沉降變形）時,分別模擬了2 塊、4 塊和6 塊變形板范圍內基礎變形,具體基礎變形調整位置如圖15所示。

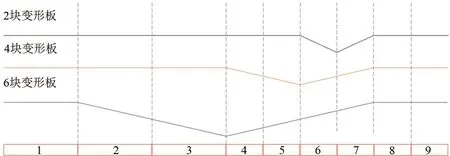
圖15 沉降變形調整位置

目前基礎變形的控制標準在15 mm/20 m,而根據過渡段軌面坡度不超過1‰的控制標準推導,在模擬的近40 m 軌道—路基模型中,不均勻變形量也不得超過40 mm,因此,本文基礎變形加載量取為±15 mm,模擬的基礎變形量為±60 mm,涵蓋既有變形控制標準與現場調研所獲取的最大不均勻變形量。

3.5 路基變形模擬試驗測試方法

為了測試基礎變形過程中,變形在路基內部以及傳遞至無砟軌道表面的擴散過程,需要在試驗填筑路基內部設置可以捕捉不同位置處豎向變形的多層位移傳感器。本文在充分調研相對變形測試方法的基礎上,提出了用全向位移計和物位計2 種方法對基礎變形擴散過程及對無砟軌道的影響進行測試。

為確保試驗結果準確,將試驗用全向位移計及物位計布置于同一層相同位置處相互校驗。傳感器均在模擬地基內布置,共3層,最底層布置在變形板表面,中間層布置于地基高度0.5 m 位置處,頂層布置于地基高度1 m 位置處。縱向上傳感器對應布置在節段變形板縫位置處。具體布置方案如圖16所示。

按照地基土厚度施工過程,分階段安裝傳感器,傳感器現場安裝情況如圖17所示。

4 試驗結果驗證

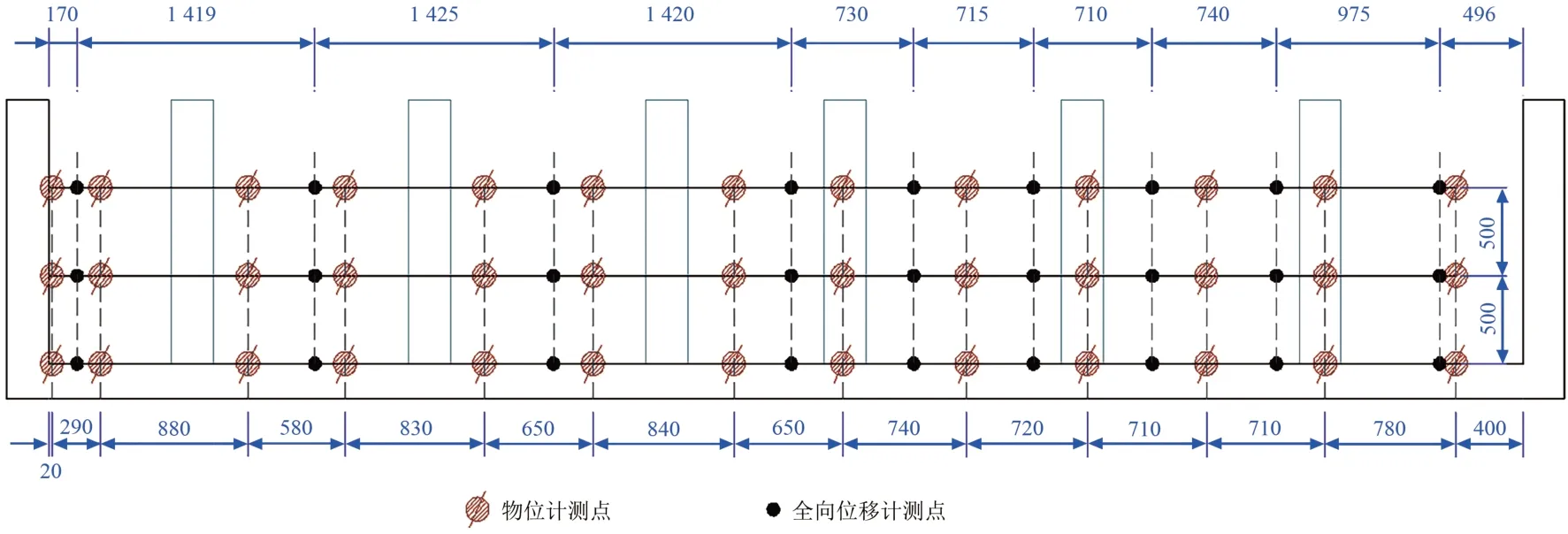
圖16 傳感器布置圖（單位：mm）

圖17 傳感器現場安裝

為分析路基傳遞規律測試結果,建立與現場試驗模型相近的仿真分析模型,對基礎變形模擬過程進行了仿真分析,與實測結果進行對比。建立模型中包含沉降板、圍擋、立柱等邊界條件,以及地基、無砟軌道等變形主體。模型中地基與圍擋間設置可分離的接觸邊界,摩擦系數取為0.2,地基內中砂與細砂的回彈模量測試結果相差較小,分別取為25和15 MPa。所建立的模型如圖18所示。

路基厚度0.5 m,最大實際沉降變形下,不同基礎變形波長時地基內沉降變形云圖如圖19所示。

底層和頂層的變形曲線與實測變形曲線對比如圖20所示。

仿真結果與測試結果對比表明,實測變形量與仿真分析所得計算曲線能夠較好地重合,波長較短時,沉降傳遞至上層時量值衰減越明顯,波長越長時,沉降峰值衰減越小。

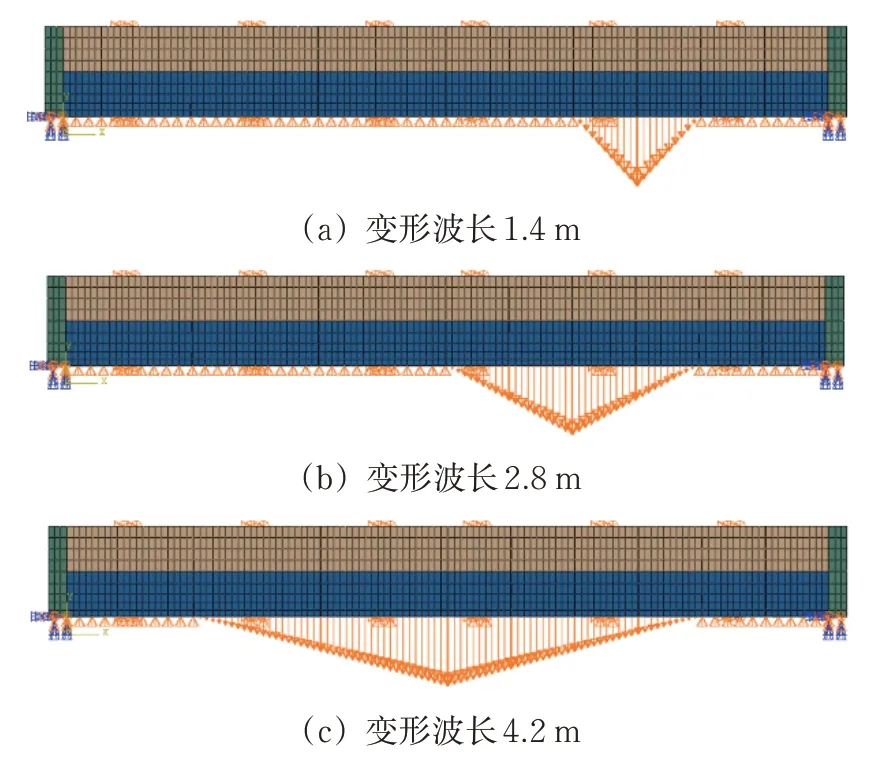
圖18 路基變形模擬試驗驗證模型

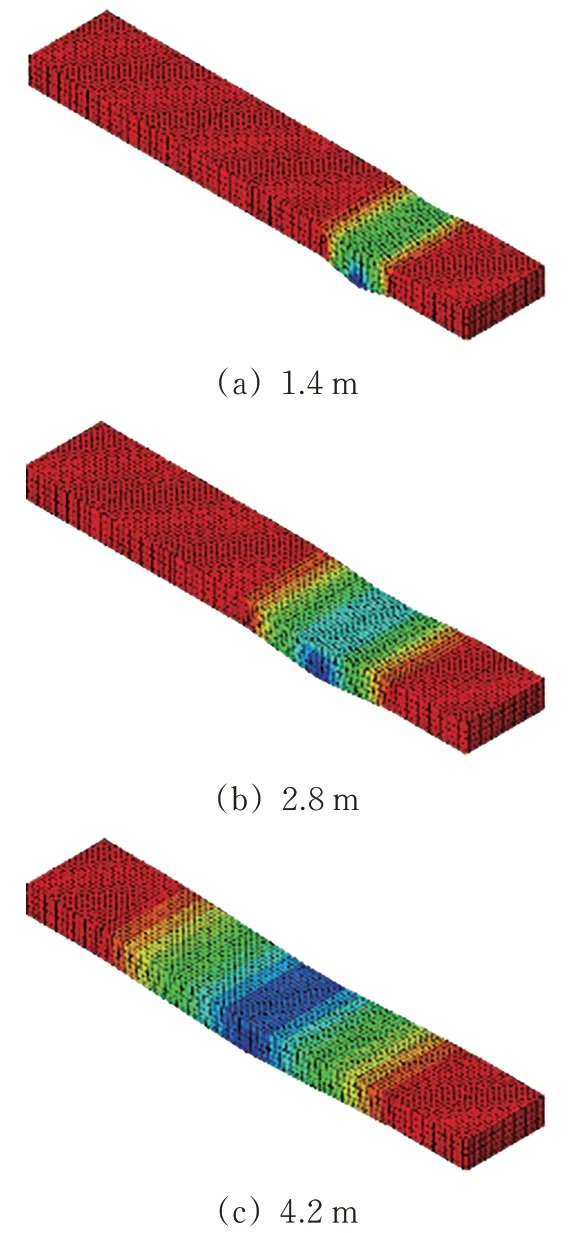
圖19 路基變形模擬試驗驗證模型

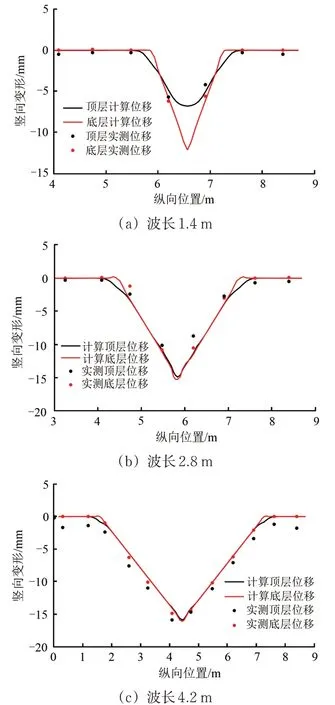
圖20 測試結果與理論分析結果對比驗證

5 結 論

（1）提出了無砟軌道—路基變形量綱相似模型設計準則：原型與模型尺寸比例為1：n時,材料彈性模量比例1：n、加載位移比例為1：n、重度γ比例為1：1、扣件剛度1：n2時,滿足量綱相似準則,此時結構變形比例為1：n,應力比例為1：n。

（2）直接縮尺模型時,基礎變形曲線吻合較好,但軌道板及底座板變形與實尺模型間差異較大,軌道板及底座應力分布也與實尺模型差異較大,無法直接推廣至原型。采用相似模型時原型與模型的應力與變形基本一致,相似模型試驗結果可直接推廣至原型。

（3）在試驗比選基礎上,提出模型與原型比例為1：4的無砟軌道—路基變形相似模擬試驗平臺設計方案,采用中砂、細砂模擬路基材料,用摻膨潤土砂漿模擬無砟軌道混凝土材料。通過底部節段變形板的設置實現不同變形波長的模擬,通過豎向調整裝置實現沉降、上拱等不同路基變形量的模擬。

（4）依據本文提出方法搭建的試驗平臺實測變形曲線與仿真分析所得計算曲線能夠較好地重合,驗證了試驗方法可靠性。初步試驗表明,波長較短時,沉降傳遞至上層時峰值衰減越明顯,波長越長時,沉降峰值衰減越小。