電氣化鐵路混合寬頻濾波器研究

周福林，陳志遠，熊進飛

（西南交通大學 電氣工程學院,四川 成都 611756）

我國電氣化鐵路的電力機車和動車組（簡稱機車）,分別采用基于相控整流的交—直型傳動方式和基于脈寬調制（Pulse Width Modulation,PWM）整流的交—直—交型傳動方式。交—直型機車通過控制晶閘管觸發角的大小調節直流側電壓,其特征諧波主要集中在3,5和7 次等低頻段諧波；交—直—交型機車采用PWM 技術,雖輸出的低次諧波減少,但開關頻率附近的高次諧波增加,輸出的主要諧波可廣泛分布在20～100 次之間［1-5］。交—直型和交—直—交型機車共線混跑在未來較長一段時間內會長期存在,使得3～100 次寬頻諧波將長期存在于牽引供電系統中［6］。運行實踐表明,寬頻諧波增加了諧波與線路發生共振的風險,易造成接觸網和機車車頂的避雷器、互感器炸裂,線路補償電容器、機車RC 電路損壞［7］,輔助供電系統直流電壓抬升［8］,變電所低壓電氣設備損壞等故障［9］。

目前抑制電氣化鐵路寬頻諧波主要從無源治理、有源治理、混合治理3個方面入手。在無源治理方面,應用于電氣化鐵路中的無源濾波器較多采用在地面安裝單調諧濾波器［10］、2 階高通濾波器［11］、阻波高通濾波器［12］,這對電氣化鐵路諧波諧振起到了較好的抑制效果,但只能對特定次或某一高頻帶的諧波進行治理,動態補償性能較差,且易與牽引供電系統電源側等效阻抗發生諧振；文獻［13］提出了安裝C型濾波器及C型與單調諧濾波器組合的2 種濾波方案,并從濾波效率、成本等方面評估這2 種方案的應用價值,但這2 種方案對系統參數很敏感,易與系統側等效阻抗發生諧振；文獻［14］提出將機車車載變流器網側L型濾波器替換為LCL 型濾波器,通過輔以相應的控制算法抑制牽引網諧波諧振,但增加了機車的體積和重量,不利于車輛輕量化的發展要求。在有源治理方面,文獻［15］提出使用有源電力濾波器（Active Power Filter,APF）完成對諧波的動態治理,APF 雖克服了無源濾波器的缺陷,但受開關器件容量和耐壓的限制,難以適用于高電壓、大容量場合；文獻［16］提出采用降壓變壓器降低牽引網電壓后接入APF,但變壓器的引入增加了牽引供電系統的復雜性和相應的成本；文獻［17-18］提出基于級聯多電平技術的APF,能夠適用于大容量、高電壓的場合,但其拓撲結構和控制策略較為復雜。以上有源治理技術中,APF 難以跟蹤高次諧波,因此難以對高次諧波進行治理。在混合治理方面,文獻［19-20］提出有源與無源濾波器相結合的混合有源濾波器,其有源部分不直接承受基波電壓,文獻［19］中的晶閘管投切濾波器會阻礙有源部分發出的諧波電流,文獻［20］中的基波諧振支路會使注入諧波分流,降低有源部分的補償效率。以上混合治理技術主要以降低APF 承受電壓為目的,其濾波范圍在3～9 次諧波范圍內。

本文提出在牽引供電系統地面變電所安裝一種混合寬頻濾波器（Hybrid Wideband-harmonics Filter,HWF）,HWF 由無源部分和有源部分構成,無源部分和有源部分分別對高次和低次諧波進行補償。通過在有源部分前端添加基波諧振電路從而阻止基波電流通過,進而降低有源部分的基波電壓；同時設置3,5 次諧波諧振電路避免有源部分發出的補償電流被分流,確保有源部分補償效率。最后通過仿真和試驗驗證HWF的可行性和有效性。

1 HWF拓撲結構

HWF 拓撲結構如圖1所示。圖中：US為牽引網電壓；ZS為電源側等效阻抗；iS為流過牽引供電系統系統側的電流；iL為非線性負載（機車）產生的電流；iF為流過HWF 的電流；iB為流過阻波支路的電流；iC為APF 輸出電流；紅色實線框為有源部分,由APF、濾波電感L0和直流側電容C2組成,通過電網整流的方式向C2充電以向APF 提供必需的直流電壓Udc,有源部分的作用是補償機車產生的低次諧波電流（次數＜7）；紅色虛線框為HWF 的無源部分,由3 次諧波諧振電路（PRC3）、5 次諧波諧振電路（PRC5）、阻尼電阻R1組成的阻波支路及基波諧振電路（PRC1）構成,其中PRC1由電感L1和電容C1并聯構成,PRC3和PRC5構成同理,無源部分的作用是補償機車產生的高次諧波電流（次數≥7）,其中PRC3和PRC5分別調諧在3 和5 次頻率處,用來阻礙機車電流中的3 和5 次諧波電流流過阻波支路,同時避免APF 發出的補償電流被阻波支路分流,保障了有源部分對機車電流里面的3和5 次諧波電流進行有效補償。

圖1 HWF拓撲結構

此拓撲結構中,因為PRC1調諧于基波頻率,PRC1在基波下呈現無窮大阻抗,所以基波電流基本不流過HWF,PRC1幾乎承受全部基波電壓,保證了有源部分不承受基波電壓和電流,從而有效降低了有源部分的容量,在很大程度上克服有源部分的容量限制,更容易實現APF 在高壓場合下的應用。

2 HWF濾波原理

HWF 諧波域等效電路如圖2所示。圖中：ZF和ZB分別為PRC1阻抗和阻波支路阻抗；iSh為流過牽引供電系統系統側的諧波電流；iLh為機車產生的諧波電流；iFh為流過PRC1的諧波電流；iBh為流過阻波支路的諧波電流；UA為有源部分承受的電壓。

圖2 HWF諧波域等效電路

在圖2中,根據基爾霍夫電流和電壓定律可以得到

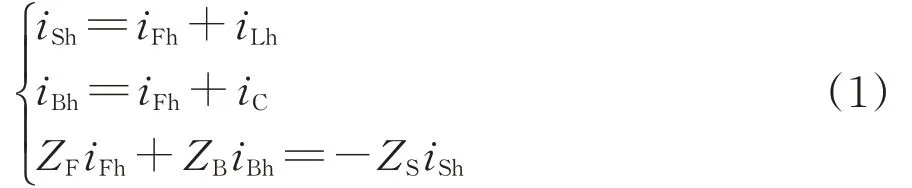
將APF輸出電流控制為

式中：K為諧波補償系數,K∈［0,1］；K=0 時,相當于只有無源部分工作；0＜K≤1時,相當于有源部分和無源部分共同工作。

由式（1）和式（2）可以解得

圖2的等效電路如圖3所示。從圖3可以看出：HWF 的有源部分在諧波域等效為與電源側等效阻抗ZS串聯的阻抗KZB,當K值取最大時,將會有最少的諧波電流流入其系統；HWF 能夠抑制無源部分阻抗與電網側等效阻抗之間的諧振。

當K=0 時,即只考慮HWF 無源部分對高次諧波的濾波作用時,由式（3）可得

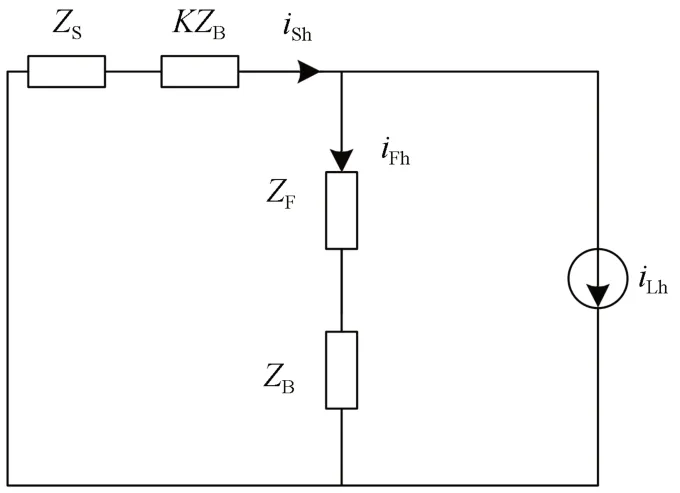
圖3 圖2等效電路

式（4）中,ZB+ZF為HWF 無源部分的阻抗,而從圖1可以看出,因為有并聯電容的存在,ZB+ZF在高次諧波下阻抗非常小,因而式（4）得到的iSh也很小,由此說明HWF 能夠對機車產生的高次諧波電流進行有效濾除。

3 HWF特性分析

3.1 HWF濾波特性

為便于后文分析,先給出1 組HWF 無源部分的典型電氣參數及系統側等效電感LS參數見表1。

表1 無源部分跟系統側等效電感的電氣參數

利用Matlab/Simulink仿真軟件對HWF無源部分阻抗進行仿真,結果如圖4所示。從圖4可以看出：HWF 的無源部分在高次諧波下阻抗非常小,能夠對高次諧波電流提供濾波通路；同時,HWF無源部分有3 個并聯諧振點,分別在50,150 和250 Hz 頻率處,能夠對基波電流和3,5 次諧波電流進行阻礙,以確保有源部分對機車產生的3,5 次諧波電流進行有效補償。

3.2 HWF有源部分承受電壓情況

HWF 無源部分由于PRC1的存在,導致基波電流無法流過HWF,根據基爾霍夫電流和電壓定律,其中UA通過圖2中紅色箭頭路徑計算,可得

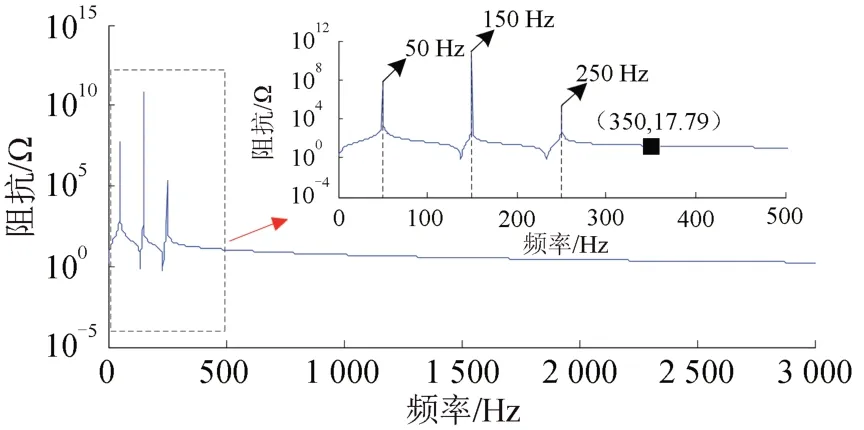
圖4 HWF無源部分阻抗頻率特性曲線

其中,

iSh=iFh+iLh

則APF承受的電壓為

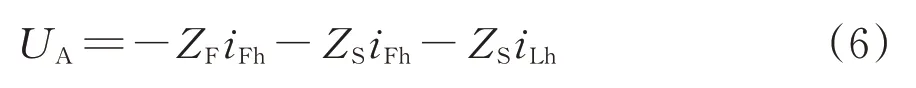
HWF工作在穩態時,流過HWF的諧波電流幾乎與負載電流里面的諧波電流相等,即iFh=-iLh,則式（6）可以簡化為

PRC1的阻抗頻率特性曲線如圖5所示。從圖5可以看出：ZF在基波的時候很大,在低次諧波時相對較小；但是在高次諧波下,ZF變得非常小。因此,在高電壓等級下,HWF 的有源部分主要承受低次諧波電壓。

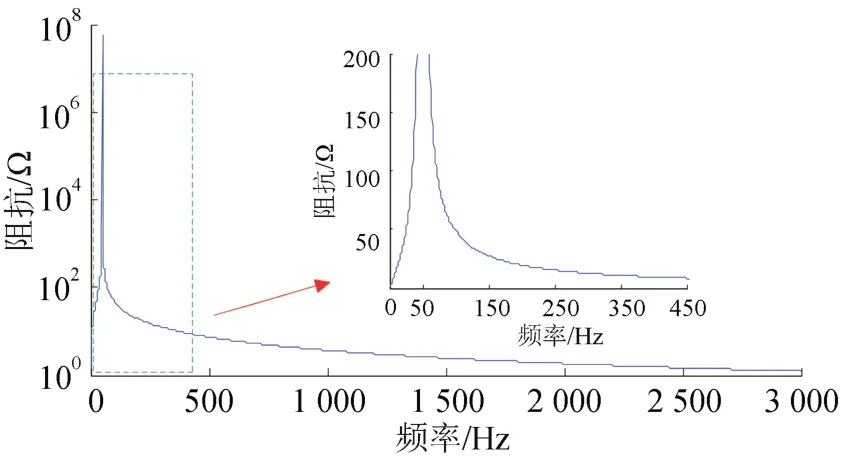
圖5 PRC1阻抗頻率特性曲線

3.3 諧波補償系數K對HWF補償特性的影響

為了驗證K值對HWF 補償性能的影響,定義流過牽引供電系統系統側的諧波電流iSh與流過機車諧波電流iLh之比為HWF 的諧波抑制能力函數,則

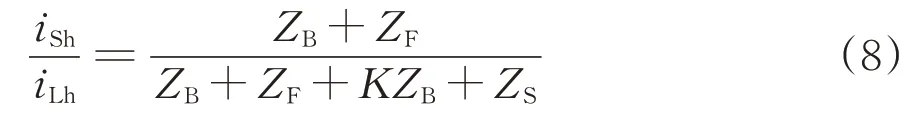
假設電源側等效阻抗為

式中：j為虛數單位；ω為角頻率。

因HWF無源部分由PRC1和阻波支路組成,則

用拉普拉斯算子s替換式（8）—式（11）中的jω可以得到復頻域中HWF 的閉環控制框圖如圖6所示。圖中：A=ZF（s）/ZB（s）,B=ZS（s）/ZB（s）。

圖6 HWF閉環控制框圖

由圖6可知HWF的閉環傳遞函數Gcolse（s）為

其中,

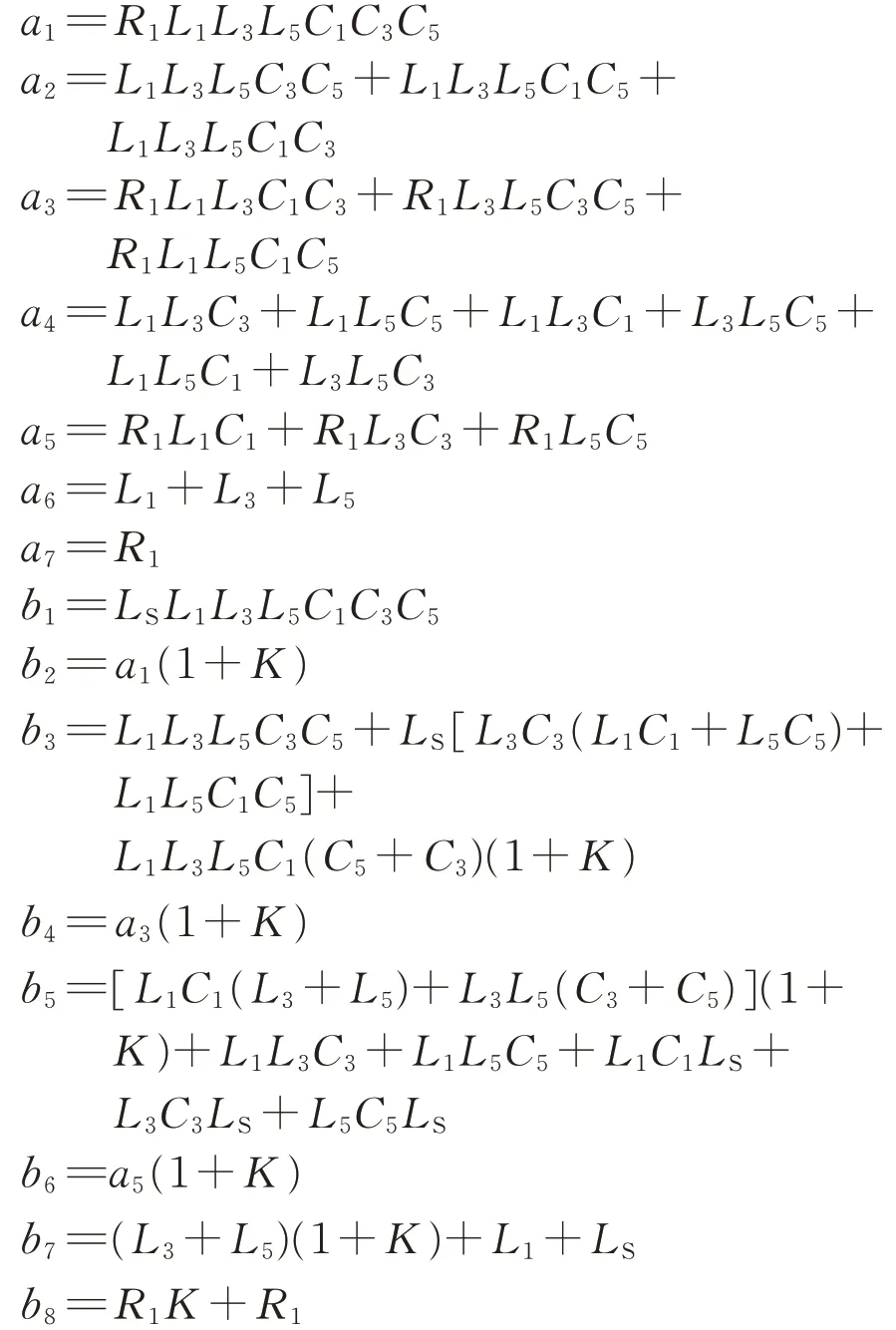
結合式（12）,當K值分別取0,0.2 及1.0 時HWF閉環傳遞函數的幅頻特性曲線如圖7所示。

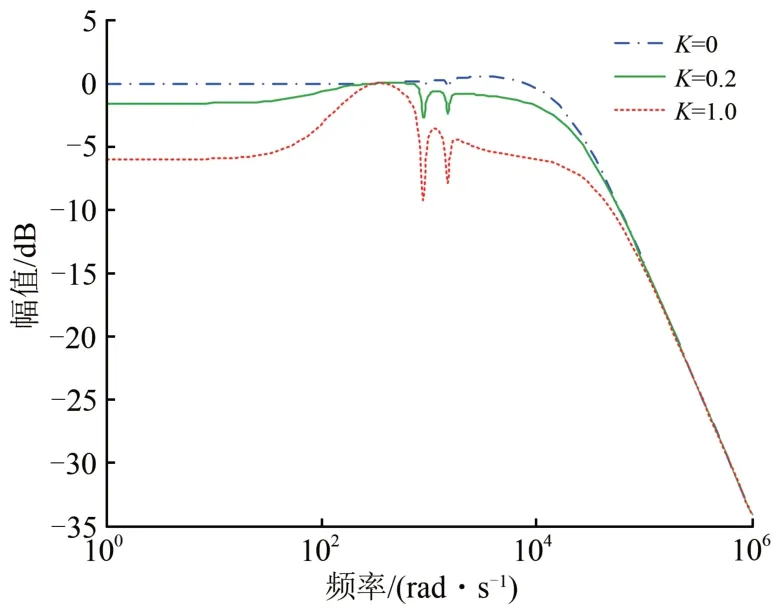
圖7 不同K值時HWF閉環傳遞函數的幅頻特性曲線

從圖7可以看出：K=0 時,相當于只考慮無源部分的補償作用,此時HWF 對高次諧波有較大的抑制作用,在ω=103～104rad·s-1之間時,HWF 的閉環傳遞函數增益大于0,但增益并未出現明顯的諧振峰值,由此說明HWF 的無源部分與系統側等效阻抗之間不會產生諧振；K≠0 時,相當于有源部分投入,HWF 的閉環傳遞函數的幅頻特性在所有的頻率段都往負半軸移動,此時HWF對各次頻率的諧波都能起到有效的抑制效果。因此,在一定范圍內,K值越大,HWF 對諧波的抑制效果越好。

3.4 HWF穩定性

由式（12）可知,HWF的特征方程為

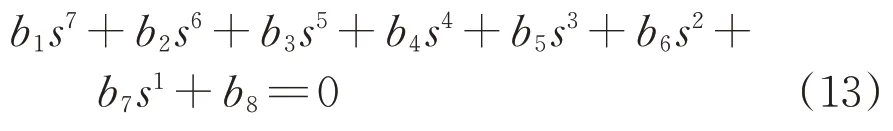
因式（13）的階次較高,該解難以直接求出,故采用勞斯判據分析HWF的穩定性。其閉環特征方程的勞斯表見表2。表中,A1=(b2b3-b1b4)/b2,B1=(A1b4-b2A2)/A1,C1=(B1A2-A1B2)/B1,D1=(C1B2-B1C2)/C1,E1=(D1C2-C1D2)/D1,F1=D2。

表2 閉環特征方程的勞斯表

由勞斯判據可知,系統穩定的充要條件是式（13）的所有系數b1—b8均為正數,且表2左數第1列的各個值也必須為正數。而式（13）的系數b1—b8本身即為正數,所以只要A1,B1,C1,D1,E1和F1均為正數即可,由此可得

分別將表1中的參數和代入表2所示的勞斯表中,發現式（14）恒成立,說明K值會影響HWF對諧波的抑制能力,但不會影響HWF的穩定性。

4 HWF控制策略

諧波電流檢測電路采用單相任意次諧波電流檢測［20］,如圖8所示。圖中：sin（kωt）和cos（kωt）為通過鎖相環（PLL）得到的頻率為牽引網基波電壓k倍的單位正余弦信號,k取3 和5；LPF 為低通濾波器。

圖8 仿真結構圖

由于三角載波控制具有固定的開關頻率,動態響應好的優點［21］,因此仿真時采用三角載波控制的方法,將APF 輸出的實際補償電流iC與檢測的指令電流iC*的差值送入PI 調節器,將調節結果uC作為調制波,通過對三角載波進行調制得到PWM波,驅動APF輸出期望的補償電流。

5 仿真及試驗驗證

5.1 仿真結果

為驗證HWF 在牽引供電系統中對寬頻諧波治理的有效性和正確性,在Matlab/Simulink 仿真軟件中根據圖8搭建仿真模型。其中包括220 kV 外部系統電源、V/x 牽引變壓器、牽引網、1 個AT所、1 個分區所、電力機車、HWF 等。牽引網為AT 全并聯運行方式,由上行的接觸線T1、鋼軌R1、正饋線F1、加強導線P1、下行的接觸線T2、鋼軌R2、正饋線F2、加強導線P2構成,其中Yp和Zp分別為線路π 型等值電路的等值阻抗和等值導納［22］。機車采用四象限運行的整流器模型等效,能夠產生低次和高次諧波電流,運行于距離牽引變電所15 km處。HWF的有源部分被控制為諧波電流源,其中K=1,L0=25 mH,直流側電壓為2 kV。牽引供電系統仿真參數見表3。

表3 牽引供電系統仿真參數

牽引供電系統系統側電流波形如圖9所示,其中HWF 的無源和有源部分分別于0.04和0.10 s時刻投入工作。圖9中所示各個階段系統側電流的頻譜圖如圖10所示。

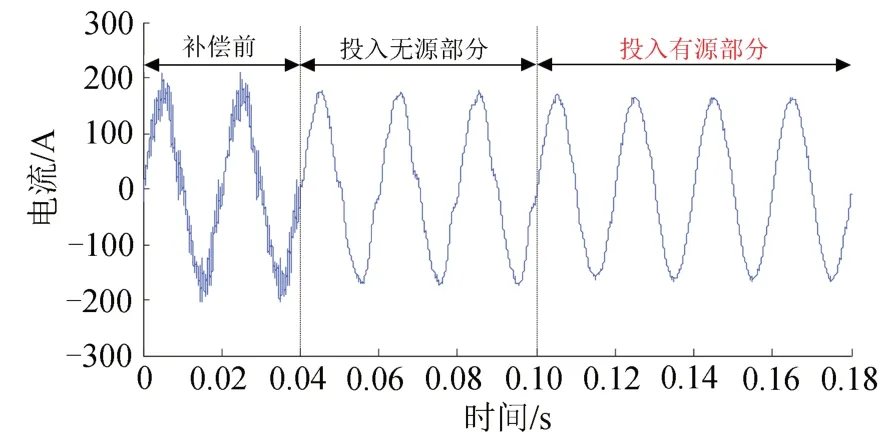
圖9 牽引供電系統系統側電流波形

圖10 各個階段系統側電流的頻譜圖

由圖9和圖10可以看出：補償前,牽引供電系統系統側電流含有低次和高次諧波成分,此時的電流總諧波畸變率（Total Harmonic Distortion,THD）為18.57%,電流波形畸變嚴重；而當無源部分投入工作后,牽引供電系統系統側電流的高次諧波成分經無源部分濾除后,只含有低次諧波電流成分,此時電流THD 由原來的18.57%降為10.67%；在0.10 s時刻投入有源部分后,此時系統側電流里面的低次諧波被有源部分補償,電流THD 降為2.41%,且系統側電流波形有很高的正弦度。

牽引網電壓波形如圖11所示。由圖11可以看出：補償前,牽引網發生了諧振,牽引網電壓波形畸變嚴重；而當HWF 投入運行后,牽引網電壓波形有很高的正弦度。

圖11 牽引網電壓波形

有源部分承受的電壓及其頻譜圖如圖12所示。由圖12可以看出：相比較于27.5 kV 的牽引網電壓,有源部分承受的電壓不超過1 000 V（瞬時值）,有源部分承受的電壓大幅度降低；同時對比圖12（a）和圖12（b）,可以驗證如前3.2 節所述的有源部分基本不承受基波電壓、主要承受低次諧波電壓的特點。因此,HWF 適用于中高壓電力系統寬頻諧波的治理。

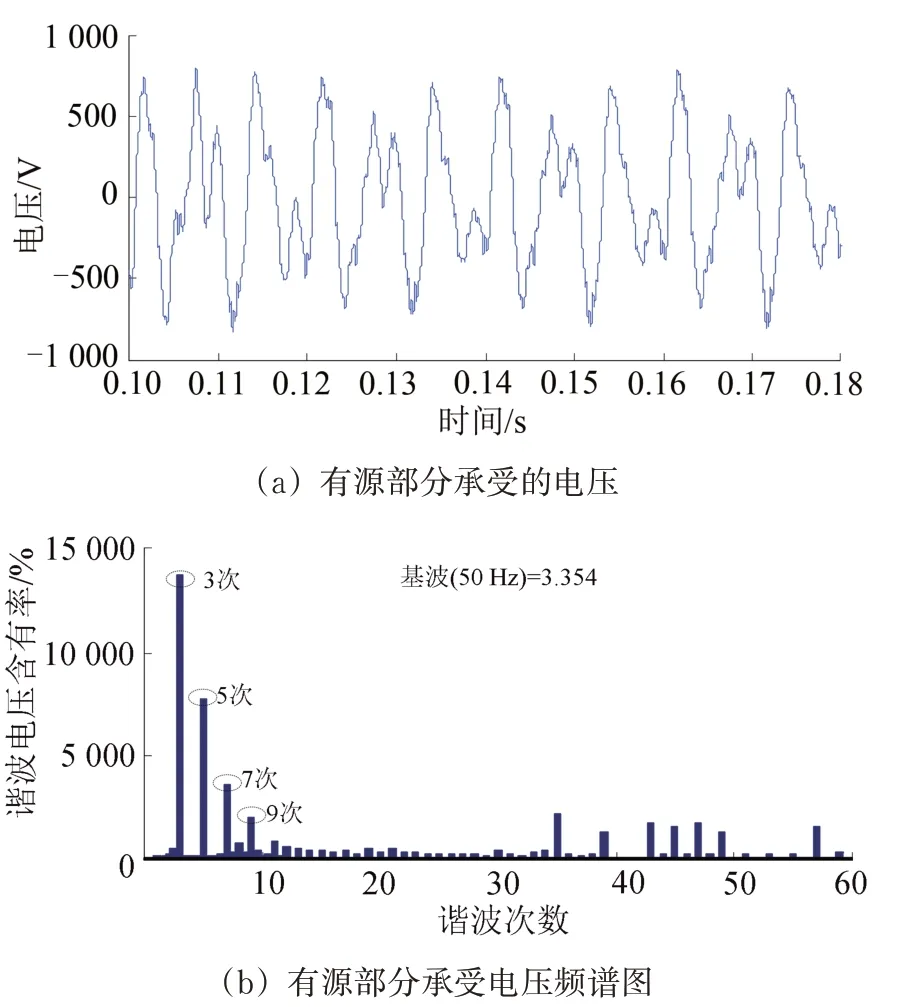
圖12 有源部分承受的電壓及其頻譜圖

5.2 試驗結果

為進一步驗證HWF 對寬頻諧波的濾波性能,根據圖1所示的單相等效電路建立試驗平臺。控制器硬件選用Altera 公司的第3 代FPGA 芯片EP4C10F17C8N。諧波源為二極管整流橋,其電阻負載初始為20 Ω（突變至10 Ω）,試驗系統參數見表4。

將表4中的參數代入表2中,式（14）恒成立,說明試驗系統穩定。電阻負載從20 Ω 突變為10 Ω時的試驗波形如圖13所示。從圖13可以看出,負載突變前后,試驗系統系統側電流一直都為正弦波,說明HWF具有很好的動態補償效果。

表4 試驗系統參數

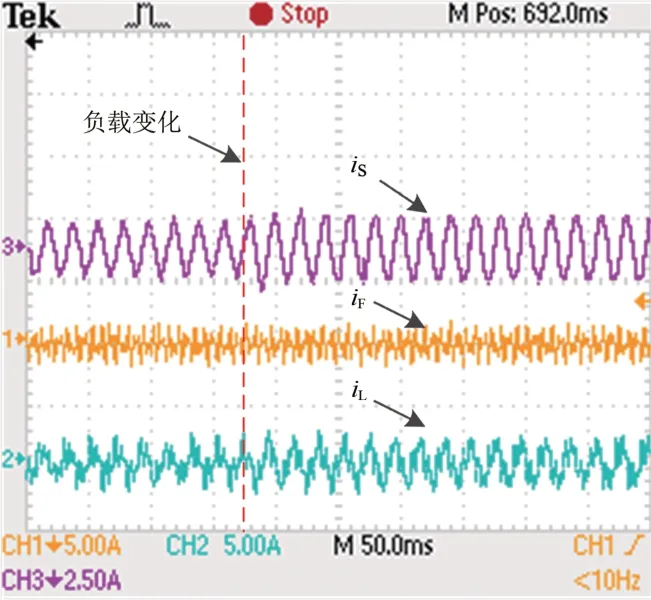
圖13 電阻負載從20 Ω突變為10 Ω時的試驗波形

HWF 穩態運行時的試驗波形如圖14所示。從圖14可以看出：有源部分主要承受低次諧波電壓,且相比較于系統電壓US有所降低。

圖14 HWF穩態運行的試驗波形

HWF 補償前后試驗系統系統側電流頻譜圖如圖15所示。從圖15可以看出：補償前,系統側電流THD 為20.0%,主要含有3 和5 次諧波電流分量；補償后,系統側電流THD 為2.5%,特征次諧波電流得到充分衰減。

圖15 HWF補償前后試驗系統系統側電流頻譜圖

6 結 論

（1）混合寬頻濾波器HWF 能夠大大改善無源部分的諧波補償性能,能夠對寬頻諧波電流進行良好的補償；同時,HWF 能夠很好地抑制無源部分阻抗與電網阻抗之間的諧振。

（2）基波諧振電路PRC1設計的目的是用來承受高電壓,降低HWF 的有源部分承受的基波電壓；有源部分只補償系統側電流的低次諧波成分,這樣可以有效降低有源部分容量,使得經濟性更高。

（3）3次諧波諧振電路PRC3和5次諧波諧振電路PRC5能夠阻止3次和5次諧波電流跟有源部分發出的3 次和5 次諧波電流流過阻波支路,保證HWF有源部分的補償效率。